Hoe de eenheidscirkel te onthouden

Het leren van de eenheidscirkel helpt je niet alleen in trigonometrie en geometrie, maar ook in toekomstige calculuscursussen. Het lijkt misschien veel om te onthouden, maar als je eenmaal begrijpt hoe het werkt, kun je beginnen met een paar cijfers en snel de rest achterhalen.

Deel een van de twee:
Radians onthouden

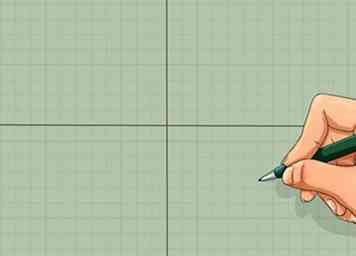1. 1 Teken twee loodrechte lijnen. Plaats een liniaal op een groot vel papier. Teken een verticale en een horizontale lijn. Deze moeten elkaar kruisen in de buurt van het midden van de pagina. Dit zijn de X en Y assen van een grafiek.
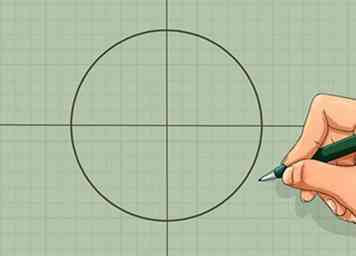2. 2 Teken een cirkel. Teken met behulp van een kompas een grote cirkel met zijn middelpunt op de kruising van de twee lijnen.
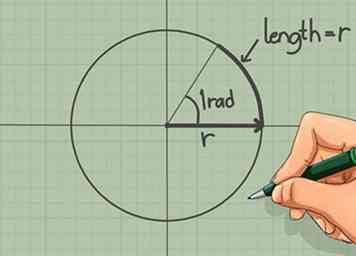3. 3 Radians begrijpen. Een radiaal is een maat voor de hoek. In het bijzonder wordt het zodanig gedefinieerd dat een persoon rond een cirkel loopt met een radius van 1 eenheid veegt over een hoek van een radiaal na het lopen voor 1 eenheid rond de omtrek. In de volgende stap labelen we de vier coördinaatpunten met de radiale waarde. Als je de formule onthoudt om de omtrek en straal te relateren, kun je deze snel uit het niets berekenen, zelfs als je ze niet hebt onthouden.
   • De radianemetingen van de eenheidscirkel gaan er altijd van uit dat u start vanaf de (0, 1) coördinaat. Om duidelijk te maken naar welk punt we verwijzen, beschrijven we de cirkel als een kompasroos:
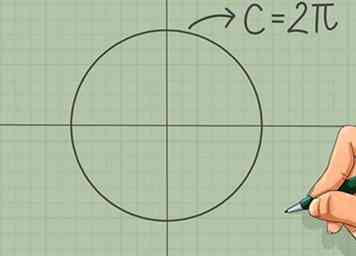4. 4 Onthoud dat de omtrek van de cirkel 2π is. De omtrek van een cirkel is gelijk aan 2πr, waar r is de straal. Omdat de eenheidscirkel een straal van 1 heeft, kunnen we de omtrek ervan vereenvoudigen tot 2π. Je kunt de radiale waarde van elk punt op de omtrek vinden, gewoon door 2π te nemen en te delen door de fractie van de cirkel die je hebt bedekt. Dit is veel eenvoudiger dan elke waarde in de cirkel te onthouden.
5. 5 Label de vier punten op de x- en y-assen. Dit alles is nodig om 2π in kwartalen te verdelen:
   • "Oost" is het startpunt, dus je hebt het behandeld 0 radialen.
   • "Noorden" = ¼ van de omtrek = ^2π/₄ = ^π/₂ radialen.
   • "Westen" = halverwege = ^2π/₂ = π radialen.
   • zuiden = driekwart over = 2π * ¾ = ^3π/₂ radialen.
   • Als u over de hele omtrek loopt, keert u terug naar uw startpunt. Je kunt dit labelen 2π evenals 0 om dit te vertegenwoordigen.
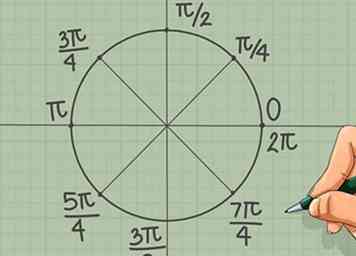6. 6 Verdeel de cirkel in achtsten. Teken nu een lijn door elk kwadrant en snijd het perfect doormidden. Nogmaals, gebruik divisie om de waarde in radialen te vinden:
   • ^π/₄
   • ^3π/₄
   • ^5π/₄
   • ^7π/₄
   • (π / 2, π, 3π / 2 en 2π zijn al gelabeld.)
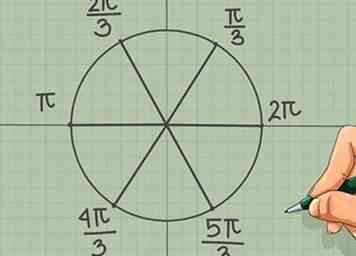7. 7 Verdeel de cirkel in zes segmenten. Teken nu extra lijnen en snijd de cirkel in zes segmenten. (Je kunt hiervoor een gradenboog gebruiken, beginnend bij de positieve x-as en telkens 60 graden.) Je kunt dezelfde bovenstaande benadering gebruiken om te realiseren dat een zesde cirkel omcirkelt ^2π/₆ = ^π/₃ radialen. Gebruik dit om de volgende punten op de omtrek te labelen (één in elk kwadrant):
   • ^π/₃
   • ^2π/₃
   • ^4π/₃
   • ^5π/₃
   • (π en 2π zijn al gelabeld)
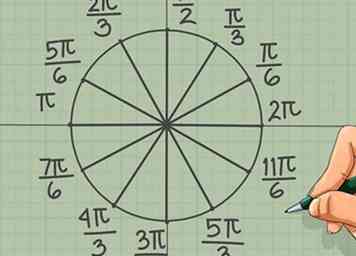8. 8 Teken in de twaalfde. De laatste punten die op de meeste eenheidscirkels worden vermeld, vertegenwoordigen stappen van een twaalfde van de omtrek. Slechts vier hiervan zijn nog niet geëtiketteerd:
   • ^π/₆
   • ^5π/₆
   • ^7π/₆
   • ^11π/₆

Deel twee van twee:
X-Y-coördinaten onthouden (Cosine, Sine)

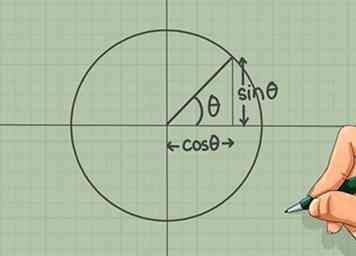1. 1 Begrijp cosinus en sinus. De eenheidscirkel is vooral handig voor trigonometrie met rechte hoeken. Elke x-coördinaat van een punt op de cirkel is gelijk aan cosinus (θ) en elke y-coördinaat is gelijk aan sinus (θ), waarbij θ de waarde van de hoek is.
   • Als je dit moeilijk kunt onthouden, denk dan (cos, sin) "want sinus goes last".
   • Je kunt dit afleiden met behulp van de juiste driehoeken en de definitie van deze functies - onthoud "sohcahtoa"?
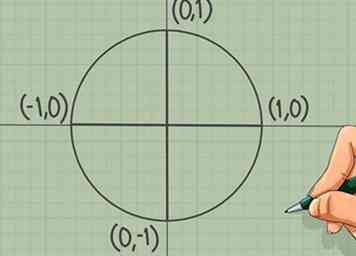2. 2 Schrijf de coördinaten op vier punten van de cirkel. Een "eenheidscirkel" is slechts een cirkel met een straal die exact één eenheid lang is. Gebruik dit om de. Te vinden X en Y coördinaten van vier punten op de cirkel, waar deze de as kruist. (We noemen dit 'Oost', 'Noord' enzovoort om het lezen te vergemakkelijken, maar dit zijn geen officiële namen.)
   • De coördinaten van het "Oostpunt" zijn (1, 0).
   • Het "noorden" -punt is om (0, 1).
   • Het 'West'-punt is om (-1, 0).
   • Het "Zuiden" punt is om (0, -1).
   • Dit werkt net als een normale grafiek. Je zou deze coördinaten alleen moeten kunnen berekenen, zonder ze te hoeven onthouden.
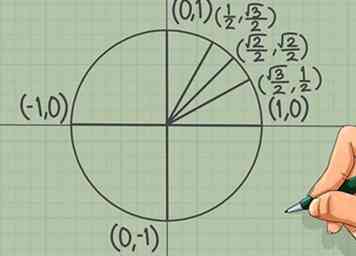3. 3 Onthoud coördinaten voor het eerste kwadrant. Het eerste kwadrant is de rechterbovenhoek van de cirkel, waar beide X en Y waarden zijn positief. Dit zijn de enige coördinaatwaarden die u moet onthouden:
   • Op ^π/₆, de coördinaten zijn ($\ displaystyle \ frac \ sqrt 3 2, \ frac 1 2$).
   • Op ^π/₄, de coördinaten zijn ($\ displaystyle \ frac \ sqrt 2 2, \ frac \ sqrt 2 2$).
   • Op ^π/₃, de coördinaten zijn ($\ displaystyle \ frac 1 2, \ frac \ sqrt 3 2$).
   • Merk op dat er slechts drie tellers zijn. Bewegen in een positieve richting (van links naar rechts voor X waarden, van onder naar boven voor Y waarden), deze moeten gaan 1 → √2 → √3.
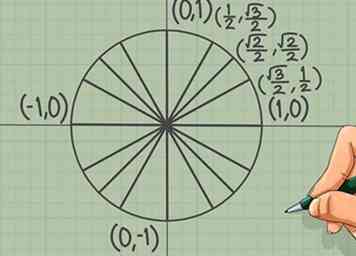4. 4 Teken rechte lijnen om andere coördinaten in te vullen. Als u een perfect verticale of een perfect horizontale lijn tussen twee punten kunt tekenen, hebben ze dezelfde absolute waarde x- en y-coördinaten. Met andere woorden, u kunt een lijn tekenen vanaf een punt in de eerste kwadranten, op dezelfde coördinaten schrijven op het punt waar u terechtkomt en laat ruimte rechts in het teken (+ of -).
   • U kunt bijvoorbeeld een horizontale lijn tekenen tussen ^π/₃ en ^2π/₃. Omdat de coördinaten op het eerste punt ($\ displaystyle \ frac 1 2, \ frac \ sqrt 3 2$), zijn de coördinaten op het tweede punt (?$\ displaystyle \ frac 1 2,? \ frac \ sqrt 3 2$), waar "?" staat klaar voor een + of - teken.
   • Hier is een snelkoppeling: controleer de noemer in de radialen. Alle punten die eindigen op / 3 hebben dezelfde coördinaten van de absolute waarde, net als alle punten die eindigen op / 4 en alle punten eindigen op / 6.
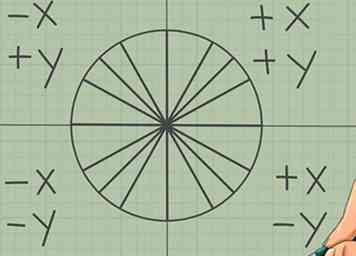5. 5 Gebruik symmetrie om uit te zoeken of het positief of negatief is. Er zijn verschillende manieren om te onthouden waar je de - tekens in je cirkel moet zetten:
   • Denk aan elementaire grafiekregels. Boven de X as is positief, hieronder is negatief. Links van de Y as is negatief, rechts is positief.
   • Begin vanuit kwadrant 1 en teken lijnen naar andere punten. Als de lijn de Y as, verandert de y-waarde van teken. Als het de X as, de X waarde schakelaars teken.
   • Onthoud "Alle studenten nemen berekeningen" (ASTC), tegen de klok in. Kwadrant 1 heeft EENll positieve waarden, Q2 heeft positief Salleen in Q3 is positief Talleen angent, en Q4 heeft positief Calleen osine.
   • Welke methode u ook kiest, de tekens zijn (+, +) voor kwadrant 1, (-, +) voor kwadrant 2, (-, -) voor kwadrant 3 en (+, -) voor kwadrant 4.
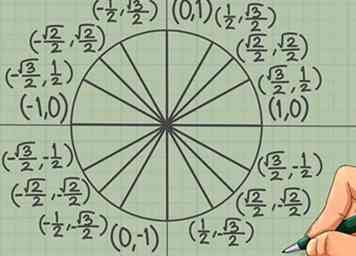6. 6 Controleer je werk. Hier is de volledige lijst met coördinaatwaarden op elk gelabeld punt in uw cirkel (de vier punten op de assen niet meegerekend), met de klok mee. Onthoud dat je al deze waarden zou moeten kunnen vinden door alleen quadrant 1 te onthouden:
   • Kwadrant 1: ($\ displaystyle \ frac \ sqrt 3 2, \ frac 1 2$); ($\ displaystyle \ frac \ sqrt 2 2, \ frac \ sqrt 2 2$); ($\ displaystyle \ frac 1 2, \ frac \ sqrt 3 2$).
   • Kwadrant 2: ($\ displaystyle - \ frac 1 2, \ frac \ sqrt 3 2$); ($\ displaystyle - \ frac \ sqrt 2 2, \ frac \ sqrt 2 2$); ($\ displaystyle - \ frac \ sqrt 3 2, \ frac 1 2$)
   • Kwadrant 3: ($\ displaystyle - \ frac \ sqrt 3 2, - \ frac 1 2$); ($\ displaystyle - \ frac \ sqrt 2 2, - \ frac \ sqrt 2 2$); ($\ displaystyle - \ frac 1 2, - \ frac \ sqrt 3 2$)
   • Kwadrant 4: ($\ displaystyle \ frac 1 2, - \ frac \ sqrt 3 2$); ($\ displaystyle \ frac \ sqrt 2 2, - \ frac \ sqrt 2 2$); ($\ displaystyle \ frac \ sqrt 3 2, - \ frac 1 2$)