Goniometrie is de tak van de wiskunde die driehoeken en cycli bestudeert. Trigonometrische functies worden gebruikt om eigenschappen van elke hoek, relaties in elke driehoek en de grafieken van elke terugkerende cyclus te beschrijven. Het leren van trigonometrie helpt je om deze relaties en cycli te visualiseren en in kaart te brengen. Als je studeren op je eentje combineert met geconcentreerd blijven in de klas, zul je de basisgoniometrische concepten begrijpen en waarschijnlijk cycli in de wereld om je heen waarnemen.
Methode één van de vier:
Focussen op belangrijke trigonometrische ideeën
-
 1 Definieer de delen van een driehoek. In de kern is trigonometrie de studie van relaties in driehoeken. Een driehoek heeft drie zijden en drie hoeken. Per definitie is de som van hoeken voor elke driehoek 180 graden. U moet vertrouwd raken met driehoeken en driehoeksterminologie om te slagen in trigonometrie. Enkele veelvoorkomende driehoekstermen zijn:[1]
1 Definieer de delen van een driehoek. In de kern is trigonometrie de studie van relaties in driehoeken. Een driehoek heeft drie zijden en drie hoeken. Per definitie is de som van hoeken voor elke driehoek 180 graden. U moet vertrouwd raken met driehoeken en driehoeksterminologie om te slagen in trigonometrie. Enkele veelvoorkomende driehoekstermen zijn:[1] - Hypotenusa - De langste zijde van een rechthoekige driehoek.
- Obtuse - Een hoek die groter is dan 90 graden.
- Acuut - een hoek kleiner dan 90 graden.
-
 2 Leer eenheid omcirkelen. Met een eenheidscirkel kun je elke driehoek schalen zodat de hypotenusa gelijk is aan één. Dit is handig omdat het trigonometrische functies, zoals sinus en cosinus tot procenten, met elkaar verbindt. Zodra u de eenheidscirkel begrijpt, kunt u goniometrische waarden voor een bepaalde hoek gebruiken om vragen over driehoeken met die hoeken te beantwoorden.[2]
2 Leer eenheid omcirkelen. Met een eenheidscirkel kun je elke driehoek schalen zodat de hypotenusa gelijk is aan één. Dit is handig omdat het trigonometrische functies, zoals sinus en cosinus tot procenten, met elkaar verbindt. Zodra u de eenheidscirkel begrijpt, kunt u goniometrische waarden voor een bepaalde hoek gebruiken om vragen over driehoeken met die hoeken te beantwoorden.[2] - Voorbeeld 1: De sinus van 30 graden is 0,50. Dit betekent dat de zijde tegenover een hoek van 30 graden precies de helft van de lengte van de schuine zijde is.
- Voorbeeld 2: Deze relatie kan worden gebruikt om de lengte van de hypotenusa te vinden in een driehoek die een hoek van 30 graden heeft met de zijde tegenover die hoek van 7 inch. De schuine zijde zou gelijk zijn aan 14 inch.
-
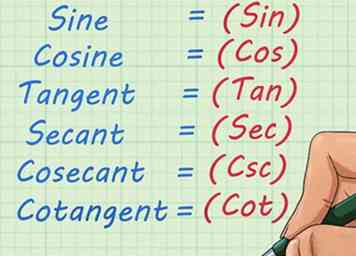 3 Ken de trigonometrische functies. Er zijn zes functies die essentieel zijn voor het begrijpen van trigonometrie. Samen definiëren ze de relaties binnen een driehoek en laten je de unieke eigenschappen van een driehoek begrijpen. Deze zes functies zijn:[3]
3 Ken de trigonometrische functies. Er zijn zes functies die essentieel zijn voor het begrijpen van trigonometrie. Samen definiëren ze de relaties binnen een driehoek en laten je de unieke eigenschappen van een driehoek begrijpen. Deze zes functies zijn:[3] - Sine (Sin)
- Cosine (Cos)
- Tangent (Tan)
- Secant (Sec)
- Cosecant (Csc)
- Cotangent (Cot)
-
 4 Relaties conceptualiseren. Een van de belangrijkste dingen om te begrijpen over trigonometrie is dat alle functies met elkaar verband houden. Hoewel de waarden voor Sine, Cosine, Tangent, enz. Allemaal hun eigen gebruik hebben, zijn ze het meest bruikbaar vanwege de relaties die er tussen bestaan. De eenheidscirkel schaalt deze relaties naar beneden, zodat ze gemakkelijk worden begrepen. Zodra u de eenheidscirkel begrijpt, kunt u de beschreven relaties gebruiken om andere problemen te modelleren.[4]
4 Relaties conceptualiseren. Een van de belangrijkste dingen om te begrijpen over trigonometrie is dat alle functies met elkaar verband houden. Hoewel de waarden voor Sine, Cosine, Tangent, enz. Allemaal hun eigen gebruik hebben, zijn ze het meest bruikbaar vanwege de relaties die er tussen bestaan. De eenheidscirkel schaalt deze relaties naar beneden, zodat ze gemakkelijk worden begrepen. Zodra u de eenheidscirkel begrijpt, kunt u de beschreven relaties gebruiken om andere problemen te modelleren.[4]
Methode twee van vier:
De toepassingen van trigonometrie begrijpen
-
 1 Begrijp het basisgebruik van trigonometrie in de academische wereld. Afgezien van het bestuderen van trigonometrie alleen voor de liefde van trigonometrie, wiskundigen en wetenschappers toepassen deze concepten. Trigonometrie kan worden gebruikt om de waarden voor hoeken of lijnsegmenten te vinden. U kunt ook alle cyclische gedragingen beschrijven door ze in grafische vorm te zetten als trigonometrische functies.[5]
1 Begrijp het basisgebruik van trigonometrie in de academische wereld. Afgezien van het bestuderen van trigonometrie alleen voor de liefde van trigonometrie, wiskundigen en wetenschappers toepassen deze concepten. Trigonometrie kan worden gebruikt om de waarden voor hoeken of lijnsegmenten te vinden. U kunt ook alle cyclische gedragingen beschrijven door ze in grafische vorm te zetten als trigonometrische functies.[5] - De beweging van een veer die heen en weer stuitert, kan bijvoorbeeld worden beschreven door deze als een sinusgolf weer te geven.
-
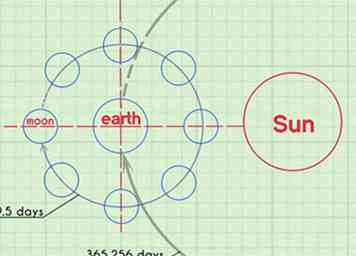 2 Denk aan cycli in de natuur. Soms worstelen mensen om abstracte concepten in wiskunde of wetenschap te begrijpen. Als je je realiseert dat die concepten aanwezig zijn in de wereld om je heen, krijgen ze vaak een nieuw licht. Zoek naar dingen in je leven die in cycli voorkomen en probeer ze in verband te brengen met trigonometrie.[6]
2 Denk aan cycli in de natuur. Soms worstelen mensen om abstracte concepten in wiskunde of wetenschap te begrijpen. Als je je realiseert dat die concepten aanwezig zijn in de wereld om je heen, krijgen ze vaak een nieuw licht. Zoek naar dingen in je leven die in cycli voorkomen en probeer ze in verband te brengen met trigonometrie.[6] - De maan heeft een voorspelbare cyclus die ongeveer 29,5 dagen lang is.
-
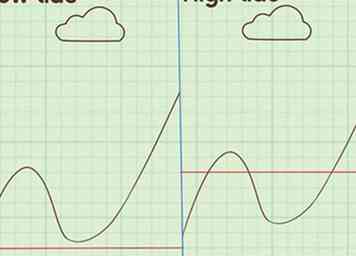 3 Visualiseer hoe natuurlijke cycli kunnen worden bestudeerd. Zodra je je realiseert dat de natuur vol cycli is, begin je erover na te denken over hoe je die cycli precies zou kunnen bestuderen. Bedenk wat een grafiek van dergelijke cycli eruit zou zien. Uit de grafiek kunt u een vergelijking formuleren om het fenomeen dat u hebt waargenomen te beschrijven. Dit geeft trigonometrische functies die u helpen het gebruik ervan te begrijpen.[7]
3 Visualiseer hoe natuurlijke cycli kunnen worden bestudeerd. Zodra je je realiseert dat de natuur vol cycli is, begin je erover na te denken over hoe je die cycli precies zou kunnen bestuderen. Bedenk wat een grafiek van dergelijke cycli eruit zou zien. Uit de grafiek kunt u een vergelijking formuleren om het fenomeen dat u hebt waargenomen te beschrijven. Dit geeft trigonometrische functies die u helpen het gebruik ervan te begrijpen.[7] - Denk aan het meten van het getij op een bepaald strand. Tijdens vloed zou het op enige hoogte zijn, en dan terugtrekken totdat het eb bereikte. Bij eb zou het water het strand opgaan totdat het weer hoogtij bereikte. Deze cyclus zou eindeloos doorgaan en zou in een grafiek kunnen worden weergegeven als een trigonometrische functie, zoals een cosinusgolf.
Methode drie van vier:
Studeren voor de toekomst
-
 1 Lees het hoofdstuk. Trigonometrische concepten zijn voor sommige mensen vaak moeilijk te begrijpen tijdens de eerste keer. Als je het hoofdstuk leest voordat je er in een klas overheen gaat, ben je meer vertrouwd met het materiaal. Hoe vaker je het materiaal ziet, hoe meer verbanden je gaat maken over hoe verschillende concepten in trigonometrie gerelateerd zijn.[8]
1 Lees het hoofdstuk. Trigonometrische concepten zijn voor sommige mensen vaak moeilijk te begrijpen tijdens de eerste keer. Als je het hoofdstuk leest voordat je er in een klas overheen gaat, ben je meer vertrouwd met het materiaal. Hoe vaker je het materiaal ziet, hoe meer verbanden je gaat maken over hoe verschillende concepten in trigonometrie gerelateerd zijn.[8] - Hiermee kun je ook begrippen waar je mee worstelt vóór de les identificeren.
-
 2 Bewaar een notebook. Door het boek bladeren is beter dan niets, maar het is niet het soort diepgaand lezen dat je helpt trigonometrie te leren. Houd gedetailleerde aantekeningen bij van het hoofdstuk dat u aan het lezen bent. Onthoud dat trigonometrie cumulatief is en dat de concepten op elkaar voortbouwen, dus als u uw aantekeningen uit eerdere hoofdstukken hebt, kunt u uw huidige hoofdstuk beter begrijpen.[9]
2 Bewaar een notebook. Door het boek bladeren is beter dan niets, maar het is niet het soort diepgaand lezen dat je helpt trigonometrie te leren. Houd gedetailleerde aantekeningen bij van het hoofdstuk dat u aan het lezen bent. Onthoud dat trigonometrie cumulatief is en dat de concepten op elkaar voortbouwen, dus als u uw aantekeningen uit eerdere hoofdstukken hebt, kunt u uw huidige hoofdstuk beter begrijpen.[9] - Noteer ook alle vragen die u de instructeur wilt stellen.
-
 3 Werk problemen uit het boek. Sommige mensen visualiseren trigonometrie goed, maar je moet ook de problemen oplossen. Om zeker te zijn dat je het materiaal echt begrijpt, probeer je voor de les wat problemen op te lossen. Op deze manier weet je precies wat je tijdens de les nodig hebt als je problemen hebt.[10]
3 Werk problemen uit het boek. Sommige mensen visualiseren trigonometrie goed, maar je moet ook de problemen oplossen. Om zeker te zijn dat je het materiaal echt begrijpt, probeer je voor de les wat problemen op te lossen. Op deze manier weet je precies wat je tijdens de les nodig hebt als je problemen hebt.[10] - De meeste boeken hebben de antwoorden op enkele problemen achterin. Hiermee kunt u uw werk controleren.
-
 4 Breng je materialen naar de les. Door je aantekeningen te maken en problemen te oefenen, krijg je een referentiepunt.Dit zal de dingen die u begrijpt, vernieuwen en u herinneren aan eventuele begrippen die u wellicht verder moet uitleggen. Zorg ervoor dat u alle vragen duidelijk maakt die u tijdens uw lezing hebt genoteerd.
4 Breng je materialen naar de les. Door je aantekeningen te maken en problemen te oefenen, krijg je een referentiepunt.Dit zal de dingen die u begrijpt, vernieuwen en u herinneren aan eventuele begrippen die u wellicht verder moet uitleggen. Zorg ervoor dat u alle vragen duidelijk maakt die u tijdens uw lezing hebt genoteerd.
Methode vier van vier:
Aantekeningen maken in de klas
-
 1 Schrijf in dezelfde notebook. Trigonometrische concepten zijn allemaal gerelateerd. Het is het beste om al uw bankbiljetten op één plaats te bewaren, zodat u kunt terugverwijzen naar eerdere opmerkingen. Wijs een specifieke notitieblok of map toe aan uw trigonometriestudies.[11]
1 Schrijf in dezelfde notebook. Trigonometrische concepten zijn allemaal gerelateerd. Het is het beste om al uw bankbiljetten op één plaats te bewaren, zodat u kunt terugverwijzen naar eerdere opmerkingen. Wijs een specifieke notitieblok of map toe aan uw trigonometriestudies.[11] - Je kunt ook oefenproblemen houden in dit boek.
-
 2 Maak trigonometrie uw prioriteit in de klas. Vermijd het gebruik van uw klastijd om te socialiseren of bij te praten over huiswerk voor een andere klas. Wanneer je in de trigonometrieles bent, zou je op het hoorcollege op nul moeten worden gesteld en problemen moeten oefenen. Schrijf notities op die de instructeur op het bord zet of anderszins als belangrijk aangeeft.
2 Maak trigonometrie uw prioriteit in de klas. Vermijd het gebruik van uw klastijd om te socialiseren of bij te praten over huiswerk voor een andere klas. Wanneer je in de trigonometrieles bent, zou je op het hoorcollege op nul moeten worden gesteld en problemen moeten oefenen. Schrijf notities op die de instructeur op het bord zet of anderszins als belangrijk aangeeft. -
 3 Blijf betrokken in de les. Vrijwilliger om problemen op het bord op te lossen of deel uw antwoorden op een oefenprobleem. Stel vragen als je iets niet begrijpt. Houd de communicatie zo open en vloeiend als uw instructeur zal toestaan. Dit zal je helpen bij het leren en genieten van trigonometrie.
3 Blijf betrokken in de les. Vrijwilliger om problemen op het bord op te lossen of deel uw antwoorden op een oefenprobleem. Stel vragen als je iets niet begrijpt. Houd de communicatie zo open en vloeiend als uw instructeur zal toestaan. Dit zal je helpen bij het leren en genieten van trigonometrie. - Als je instructeur het liefst ononderbroken college geeft, kun je je vragen voor na de les bewaren. Onthoud dat het de taak van de instructeur is om trigonometrie te leren, wees dus niet verlegen.
-
 4 Follow-up met meer oefenproblemen. Voltooi huiswerk toegewezen. Huiswerkproblemen zijn goede indicatoren voor testvragen. Zorg ervoor dat u elk probleem begrijpt. Als er geen huiswerk is toegewezen, werk dan problemen uit uw boek die de concepten weerspiegelen die in de meest recente lezing zijn behandeld.[12]
4 Follow-up met meer oefenproblemen. Voltooi huiswerk toegewezen. Huiswerkproblemen zijn goede indicatoren voor testvragen. Zorg ervoor dat u elk probleem begrijpt. Als er geen huiswerk is toegewezen, werk dan problemen uit uw boek die de concepten weerspiegelen die in de meest recente lezing zijn behandeld.[12]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Definieer de delen van een driehoek. In de kern is trigonometrie de studie van relaties in driehoeken. Een driehoek heeft drie zijden en drie hoeken. Per definitie is de som van hoeken voor elke driehoek 180 graden. U moet vertrouwd raken met driehoeken en driehoeksterminologie om te slagen in trigonometrie. Enkele veelvoorkomende driehoekstermen zijn:[1]
1 Definieer de delen van een driehoek. In de kern is trigonometrie de studie van relaties in driehoeken. Een driehoek heeft drie zijden en drie hoeken. Per definitie is de som van hoeken voor elke driehoek 180 graden. U moet vertrouwd raken met driehoeken en driehoeksterminologie om te slagen in trigonometrie. Enkele veelvoorkomende driehoekstermen zijn:[1]  2 Leer eenheid omcirkelen. Met een eenheidscirkel kun je elke driehoek schalen zodat de hypotenusa gelijk is aan één. Dit is handig omdat het trigonometrische functies, zoals sinus en cosinus tot procenten, met elkaar verbindt. Zodra u de eenheidscirkel begrijpt, kunt u goniometrische waarden voor een bepaalde hoek gebruiken om vragen over driehoeken met die hoeken te beantwoorden.[2]
2 Leer eenheid omcirkelen. Met een eenheidscirkel kun je elke driehoek schalen zodat de hypotenusa gelijk is aan één. Dit is handig omdat het trigonometrische functies, zoals sinus en cosinus tot procenten, met elkaar verbindt. Zodra u de eenheidscirkel begrijpt, kunt u goniometrische waarden voor een bepaalde hoek gebruiken om vragen over driehoeken met die hoeken te beantwoorden.[2] 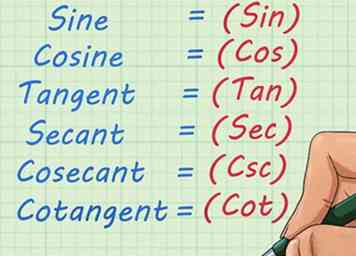 3 Ken de trigonometrische functies. Er zijn zes functies die essentieel zijn voor het begrijpen van trigonometrie. Samen definiëren ze de relaties binnen een driehoek en laten je de unieke eigenschappen van een driehoek begrijpen. Deze zes functies zijn:[3]
3 Ken de trigonometrische functies. Er zijn zes functies die essentieel zijn voor het begrijpen van trigonometrie. Samen definiëren ze de relaties binnen een driehoek en laten je de unieke eigenschappen van een driehoek begrijpen. Deze zes functies zijn:[3]  4 Relaties conceptualiseren. Een van de belangrijkste dingen om te begrijpen over trigonometrie is dat alle functies met elkaar verband houden. Hoewel de waarden voor Sine, Cosine, Tangent, enz. Allemaal hun eigen gebruik hebben, zijn ze het meest bruikbaar vanwege de relaties die er tussen bestaan. De eenheidscirkel schaalt deze relaties naar beneden, zodat ze gemakkelijk worden begrepen. Zodra u de eenheidscirkel begrijpt, kunt u de beschreven relaties gebruiken om andere problemen te modelleren.[4]
4 Relaties conceptualiseren. Een van de belangrijkste dingen om te begrijpen over trigonometrie is dat alle functies met elkaar verband houden. Hoewel de waarden voor Sine, Cosine, Tangent, enz. Allemaal hun eigen gebruik hebben, zijn ze het meest bruikbaar vanwege de relaties die er tussen bestaan. De eenheidscirkel schaalt deze relaties naar beneden, zodat ze gemakkelijk worden begrepen. Zodra u de eenheidscirkel begrijpt, kunt u de beschreven relaties gebruiken om andere problemen te modelleren.[4]  1 Begrijp het basisgebruik van trigonometrie in de academische wereld. Afgezien van het bestuderen van trigonometrie alleen voor de liefde van trigonometrie, wiskundigen en wetenschappers toepassen deze concepten. Trigonometrie kan worden gebruikt om de waarden voor hoeken of lijnsegmenten te vinden. U kunt ook alle cyclische gedragingen beschrijven door ze in grafische vorm te zetten als trigonometrische functies.[5]
1 Begrijp het basisgebruik van trigonometrie in de academische wereld. Afgezien van het bestuderen van trigonometrie alleen voor de liefde van trigonometrie, wiskundigen en wetenschappers toepassen deze concepten. Trigonometrie kan worden gebruikt om de waarden voor hoeken of lijnsegmenten te vinden. U kunt ook alle cyclische gedragingen beschrijven door ze in grafische vorm te zetten als trigonometrische functies.[5]  2 Denk aan cycli in de natuur. Soms worstelen mensen om abstracte concepten in wiskunde of wetenschap te begrijpen. Als je je realiseert dat die concepten aanwezig zijn in de wereld om je heen, krijgen ze vaak een nieuw licht. Zoek naar dingen in je leven die in cycli voorkomen en probeer ze in verband te brengen met trigonometrie.[6]
2 Denk aan cycli in de natuur. Soms worstelen mensen om abstracte concepten in wiskunde of wetenschap te begrijpen. Als je je realiseert dat die concepten aanwezig zijn in de wereld om je heen, krijgen ze vaak een nieuw licht. Zoek naar dingen in je leven die in cycli voorkomen en probeer ze in verband te brengen met trigonometrie.[6]  3 Visualiseer hoe natuurlijke cycli kunnen worden bestudeerd. Zodra je je realiseert dat de natuur vol cycli is, begin je erover na te denken over hoe je die cycli precies zou kunnen bestuderen. Bedenk wat een grafiek van dergelijke cycli eruit zou zien. Uit de grafiek kunt u een vergelijking formuleren om het fenomeen dat u hebt waargenomen te beschrijven. Dit geeft trigonometrische functies die u helpen het gebruik ervan te begrijpen.[7]
3 Visualiseer hoe natuurlijke cycli kunnen worden bestudeerd. Zodra je je realiseert dat de natuur vol cycli is, begin je erover na te denken over hoe je die cycli precies zou kunnen bestuderen. Bedenk wat een grafiek van dergelijke cycli eruit zou zien. Uit de grafiek kunt u een vergelijking formuleren om het fenomeen dat u hebt waargenomen te beschrijven. Dit geeft trigonometrische functies die u helpen het gebruik ervan te begrijpen.[7]  1 Lees het hoofdstuk. Trigonometrische concepten zijn voor sommige mensen vaak moeilijk te begrijpen tijdens de eerste keer. Als je het hoofdstuk leest voordat je er in een klas overheen gaat, ben je meer vertrouwd met het materiaal. Hoe vaker je het materiaal ziet, hoe meer verbanden je gaat maken over hoe verschillende concepten in trigonometrie gerelateerd zijn.[8]
1 Lees het hoofdstuk. Trigonometrische concepten zijn voor sommige mensen vaak moeilijk te begrijpen tijdens de eerste keer. Als je het hoofdstuk leest voordat je er in een klas overheen gaat, ben je meer vertrouwd met het materiaal. Hoe vaker je het materiaal ziet, hoe meer verbanden je gaat maken over hoe verschillende concepten in trigonometrie gerelateerd zijn.[8]  2 Bewaar een notebook. Door het boek bladeren is beter dan niets, maar het is niet het soort diepgaand lezen dat je helpt trigonometrie te leren. Houd gedetailleerde aantekeningen bij van het hoofdstuk dat u aan het lezen bent. Onthoud dat trigonometrie cumulatief is en dat de concepten op elkaar voortbouwen, dus als u uw aantekeningen uit eerdere hoofdstukken hebt, kunt u uw huidige hoofdstuk beter begrijpen.[9]
2 Bewaar een notebook. Door het boek bladeren is beter dan niets, maar het is niet het soort diepgaand lezen dat je helpt trigonometrie te leren. Houd gedetailleerde aantekeningen bij van het hoofdstuk dat u aan het lezen bent. Onthoud dat trigonometrie cumulatief is en dat de concepten op elkaar voortbouwen, dus als u uw aantekeningen uit eerdere hoofdstukken hebt, kunt u uw huidige hoofdstuk beter begrijpen.[9]  3 Werk problemen uit het boek. Sommige mensen visualiseren trigonometrie goed, maar je moet ook de problemen oplossen. Om zeker te zijn dat je het materiaal echt begrijpt, probeer je voor de les wat problemen op te lossen. Op deze manier weet je precies wat je tijdens de les nodig hebt als je problemen hebt.[10]
3 Werk problemen uit het boek. Sommige mensen visualiseren trigonometrie goed, maar je moet ook de problemen oplossen. Om zeker te zijn dat je het materiaal echt begrijpt, probeer je voor de les wat problemen op te lossen. Op deze manier weet je precies wat je tijdens de les nodig hebt als je problemen hebt.[10]  4 Breng je materialen naar de les. Door je aantekeningen te maken en problemen te oefenen, krijg je een referentiepunt.Dit zal de dingen die u begrijpt, vernieuwen en u herinneren aan eventuele begrippen die u wellicht verder moet uitleggen. Zorg ervoor dat u alle vragen duidelijk maakt die u tijdens uw lezing hebt genoteerd.
4 Breng je materialen naar de les. Door je aantekeningen te maken en problemen te oefenen, krijg je een referentiepunt.Dit zal de dingen die u begrijpt, vernieuwen en u herinneren aan eventuele begrippen die u wellicht verder moet uitleggen. Zorg ervoor dat u alle vragen duidelijk maakt die u tijdens uw lezing hebt genoteerd.  1 Schrijf in dezelfde notebook. Trigonometrische concepten zijn allemaal gerelateerd. Het is het beste om al uw bankbiljetten op één plaats te bewaren, zodat u kunt terugverwijzen naar eerdere opmerkingen. Wijs een specifieke notitieblok of map toe aan uw trigonometriestudies.[11]
1 Schrijf in dezelfde notebook. Trigonometrische concepten zijn allemaal gerelateerd. Het is het beste om al uw bankbiljetten op één plaats te bewaren, zodat u kunt terugverwijzen naar eerdere opmerkingen. Wijs een specifieke notitieblok of map toe aan uw trigonometriestudies.[11]  2 Maak trigonometrie uw prioriteit in de klas. Vermijd het gebruik van uw klastijd om te socialiseren of bij te praten over huiswerk voor een andere klas. Wanneer je in de trigonometrieles bent, zou je op het hoorcollege op nul moeten worden gesteld en problemen moeten oefenen. Schrijf notities op die de instructeur op het bord zet of anderszins als belangrijk aangeeft.
2 Maak trigonometrie uw prioriteit in de klas. Vermijd het gebruik van uw klastijd om te socialiseren of bij te praten over huiswerk voor een andere klas. Wanneer je in de trigonometrieles bent, zou je op het hoorcollege op nul moeten worden gesteld en problemen moeten oefenen. Schrijf notities op die de instructeur op het bord zet of anderszins als belangrijk aangeeft.  3 Blijf betrokken in de les. Vrijwilliger om problemen op het bord op te lossen of deel uw antwoorden op een oefenprobleem. Stel vragen als je iets niet begrijpt. Houd de communicatie zo open en vloeiend als uw instructeur zal toestaan. Dit zal je helpen bij het leren en genieten van trigonometrie.
3 Blijf betrokken in de les. Vrijwilliger om problemen op het bord op te lossen of deel uw antwoorden op een oefenprobleem. Stel vragen als je iets niet begrijpt. Houd de communicatie zo open en vloeiend als uw instructeur zal toestaan. Dit zal je helpen bij het leren en genieten van trigonometrie.  4 Follow-up met meer oefenproblemen. Voltooi huiswerk toegewezen. Huiswerkproblemen zijn goede indicatoren voor testvragen. Zorg ervoor dat u elk probleem begrijpt. Als er geen huiswerk is toegewezen, werk dan problemen uit uw boek die de concepten weerspiegelen die in de meest recente lezing zijn behandeld.[12]
4 Follow-up met meer oefenproblemen. Voltooi huiswerk toegewezen. Huiswerkproblemen zijn goede indicatoren voor testvragen. Zorg ervoor dat u elk probleem begrijpt. Als er geen huiswerk is toegewezen, werk dan problemen uit uw boek die de concepten weerspiegelen die in de meest recente lezing zijn behandeld.[12]