Het vinden van de omtrek van een driehoek betekent het vinden van de afstand rond de driehoek.[1] De eenvoudigste manier om de omtrek van een driehoek te vinden, is om de lengte van alle zijden bij elkaar op te tellen, maar als u niet alle lengte van de zijden weet, moet u ze eerst berekenen. Dit artikel leert je eerst de omtrek van een driehoek te vinden als je alle drie de lengtes kent; dit is de gemakkelijkste en meest gebruikelijke manier. Het zal je dan leren om de omtrek van een rechthoekige driehoek te vinden als slechts twee van de lengtes bekend zijn. Ten slotte zal het je leren de omtrek te vinden van een driehoek waarvan je twee lengtes kent en de hoekmaat ertussen (een "SAS-driehoek"), met behulp van de Wet van Cosinus.
Methode één van de drie:
De perimeter vinden als drie lengtes bekend zijn
-
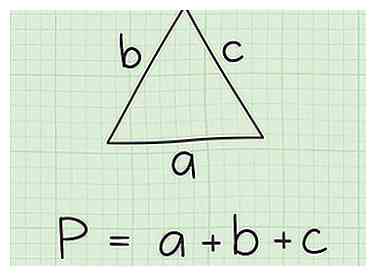 1 Denk aan de formule voor het vinden van de omtrek van een driehoek. Voor een driehoek met zijden een, b en c, de omtrek P is gedefinieerd als: P = a + b + c.
1 Denk aan de formule voor het vinden van de omtrek van een driehoek. Voor een driehoek met zijden een, b en c, de omtrek P is gedefinieerd als: P = a + b + c. - Wat deze formule in eenvoudigere bewoordingen betekent, is dat om de omtrek van een driehoek te vinden, u gewoon de lengtes van elk van de 3 zijden bij elkaar optelt.
-
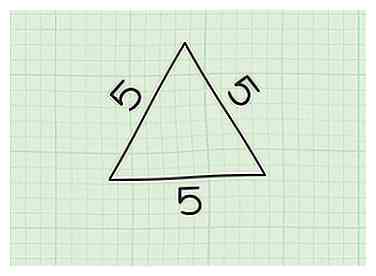 2 Kijk naar je driehoek en bepaal de lengte van de drie zijden. In dit voorbeeld de lengte van de zijkant een = 5, de lengte van de zijkant b = 5en de lengte van de zijkant c = 5.
2 Kijk naar je driehoek en bepaal de lengte van de drie zijden. In dit voorbeeld de lengte van de zijkant een = 5, de lengte van de zijkant b = 5en de lengte van de zijkant c = 5. - Dit specifieke voorbeeld wordt een gelijkzijdige driehoek genoemd, omdat alle drie zijden even lang zijn. Maar vergeet niet dat de randformule hetzelfde is voor elke soort driehoek.
-
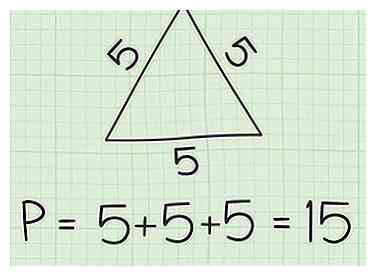 3 Voeg de drie zijlengtes samen toe om de omtrek te vinden. In dit voorbeeld 5 + 5 + 5 = 15. daarom P = 15.
3 Voeg de drie zijlengtes samen toe om de omtrek te vinden. In dit voorbeeld 5 + 5 + 5 = 15. daarom P = 15. - In een ander voorbeeld, waar a = 4, b = 3, en c = 5, de omtrek zou zijn: P = 3 + 4 + 5of 12.
-
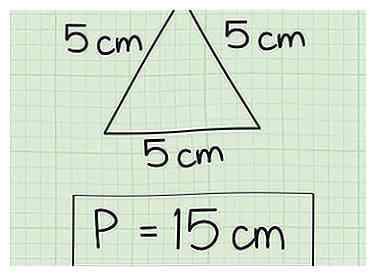 4 Vergeet niet om de eenheden op te nemen in uw definitieve antwoord. Als de zijden van de driehoek in centimeters worden gemeten, moet uw antwoord ook in centimeters zijn. Als de zijden worden gemeten in termen van een variabele zoals x, moet uw antwoord ook in termen van x zijn.
4 Vergeet niet om de eenheden op te nemen in uw definitieve antwoord. Als de zijden van de driehoek in centimeters worden gemeten, moet uw antwoord ook in centimeters zijn. Als de zijden worden gemeten in termen van een variabele zoals x, moet uw antwoord ook in termen van x zijn. - In dit voorbeeld zijn de zijlengtes elk 5 cm, dus de juiste waarde voor de omtrek is 15 cm.
Methode twee van drie:
De omtrek van een rechthoekige driehoek vinden wanneer twee zijden bekend zijn
-
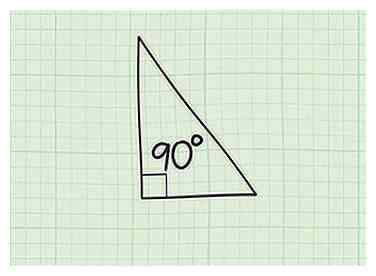 1 Onthoud wat een rechthoekige driehoek is. Een rechterdriehoek is een driehoek die één rechtse (90 graden) hoek heeft. De zijde van de driehoek tegenover de rechte hoek is altijd de langste zijde en wordt de hypotenusa genoemd. Juiste driehoeken verschijnen vaak bij wiskundetests en gelukkig is er een zeer handige formule om de lengte van onbekende zijden te vinden!
1 Onthoud wat een rechthoekige driehoek is. Een rechterdriehoek is een driehoek die één rechtse (90 graden) hoek heeft. De zijde van de driehoek tegenover de rechte hoek is altijd de langste zijde en wordt de hypotenusa genoemd. Juiste driehoeken verschijnen vaak bij wiskundetests en gelukkig is er een zeer handige formule om de lengte van onbekende zijden te vinden! -
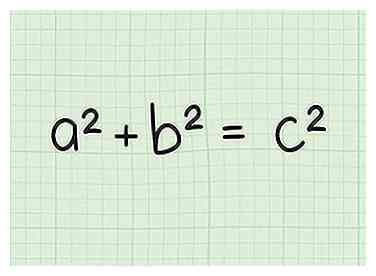 2 Denk aan de stelling van Pythagoras. De stelling van Pythagoras vertelt ons dat voor elke rechthoekige driehoek met zijden van lengte a en b en hypotenusa van lengte c, een2 + b2 = c2.[2]
2 Denk aan de stelling van Pythagoras. De stelling van Pythagoras vertelt ons dat voor elke rechthoekige driehoek met zijden van lengte a en b en hypotenusa van lengte c, een2 + b2 = c2.[2] -
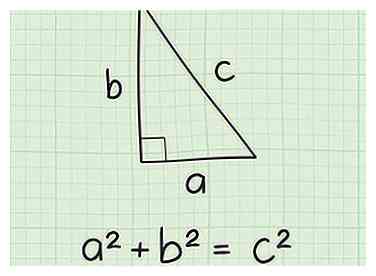 3 Kijk naar je driehoek en label de zijkanten "a", "b" en "c". Vergeet niet dat de langste zijde van de driehoek de hypotenusa wordt genoemd. Het staat tegenover de juiste hoek en moet worden geëtiketteerd c. Label de twee korte zijden een en b. Het maakt niet echt uit wat is wat, de wiskunde zal hetzelfde blijken!
3 Kijk naar je driehoek en label de zijkanten "a", "b" en "c". Vergeet niet dat de langste zijde van de driehoek de hypotenusa wordt genoemd. Het staat tegenover de juiste hoek en moet worden geëtiketteerd c. Label de twee korte zijden een en b. Het maakt niet echt uit wat is wat, de wiskunde zal hetzelfde blijken! -
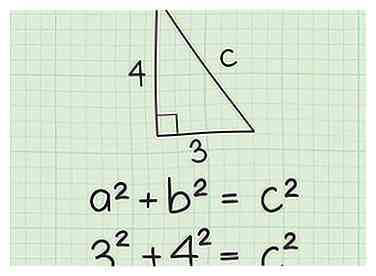 4 Voer de lengtes in die je kent in de stelling van Pythagoras. Onthoudt dat een2 + b2 = c2. Vervang de lengtes langs de zijkant voor de corresponderende letters in de vergelijking.
4 Voer de lengtes in die je kent in de stelling van Pythagoras. Onthoudt dat een2 + b2 = c2. Vervang de lengtes langs de zijkant voor de corresponderende letters in de vergelijking. - Als je bijvoorbeeld die kant kent a = 3 en kant b = 4, plug dan die waarden als volgt in de formule: 32 + 42 = c2.
- Als u de lengte van zijde kent a = 6en de hypotenusa c = 10, dan zou je de vergelijking als volgt moeten instellen: 62 + b2 = 102.
-
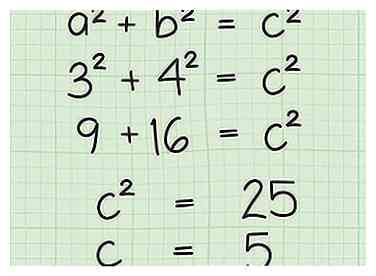 5 Los de vergelijking op om de lengte van de ontbrekende zijde te vinden. U zult eerst de bekende lengtes van de zijden moeten verdelen, wat betekent dat elke waarde afzonderlijk moet worden vermenigvuldigd (bijvoorbeeld 32 = 3 * 3 = 9). Als u op zoek bent naar de hypotenusa, voegt u eenvoudig de twee waarden bij elkaar en vindt u de vierkantswortel van dit getal om de lengte te vinden. Als het een lengte van de zijkant is die u mist, moet u een beetje gemakkelijk aftrekken doen en vervolgens de vierkantswortel nemen om uw zijde te vergroten.
5 Los de vergelijking op om de lengte van de ontbrekende zijde te vinden. U zult eerst de bekende lengtes van de zijden moeten verdelen, wat betekent dat elke waarde afzonderlijk moet worden vermenigvuldigd (bijvoorbeeld 32 = 3 * 3 = 9). Als u op zoek bent naar de hypotenusa, voegt u eenvoudig de twee waarden bij elkaar en vindt u de vierkantswortel van dit getal om de lengte te vinden. Als het een lengte van de zijkant is die u mist, moet u een beetje gemakkelijk aftrekken doen en vervolgens de vierkantswortel nemen om uw zijde te vergroten. - In het eerste voorbeeld viert u de waarden in 32 + 42 = c2 en vind dat 25 = c2. Bereken vervolgens de vierkantswortel van 25 om dat te vinden c = 5.
- Verander in het tweede voorbeeld de waarden in 62 + b2 = 102 om dat te vinden 36 + b2 = 100. Trek 36 van elke kant af om dat te vinden b2 = 64, neem dan de vierkantswortel van 64 om dat te vinden b = 8.
-
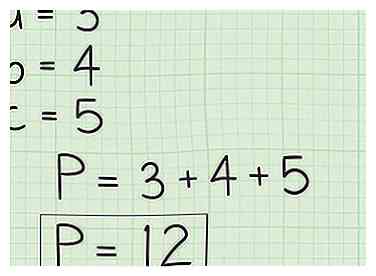 6 Tel de lengten van de drie zijlengten bij elkaar op om de omtrek te vinden. Bedenk dat de omtrek P = a + b + c. Nu dat je de lengte van zijden kent een, b en c, u hoeft alleen de lengtes bij elkaar op te tellen om de omtrek te vinden.
6 Tel de lengten van de drie zijlengten bij elkaar op om de omtrek te vinden. Bedenk dat de omtrek P = a + b + c. Nu dat je de lengte van zijden kent een, b en c, u hoeft alleen de lengtes bij elkaar op te tellen om de omtrek te vinden. - In ons eerste voorbeeld,P = 3 + 4 + 5, of 12.
- In ons tweede voorbeeld, P = 6 + 8 + 10, of 24.
Methode drie van drie:
De omtrek van een SAS-driehoek vinden met behulp van de wet van Cosinus
-
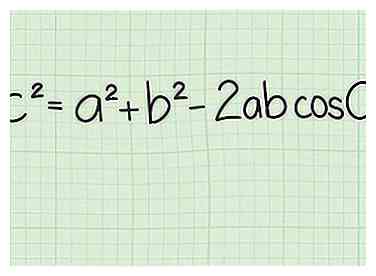 1 Leer de wet van Cosinus. De Law of Cosines stelt je in staat elke driehoek op te lossen als je twee lengtes opzij kent en de hoek ertussen meet. Het werkt op elke driehoek en is een zeer nuttige formule. De wet van Cosinus stelt dat voor elke driehoek met zijden een, b, en c, met tegenovergestelde hoeken EEN, B, en C: c2 = a2 + b2 - 2ab cos(C).[3][4]
1 Leer de wet van Cosinus. De Law of Cosines stelt je in staat elke driehoek op te lossen als je twee lengtes opzij kent en de hoek ertussen meet. Het werkt op elke driehoek en is een zeer nuttige formule. De wet van Cosinus stelt dat voor elke driehoek met zijden een, b, en c, met tegenovergestelde hoeken EEN, B, en C: c2 = a2 + b2 - 2ab cos(C).[3][4] -
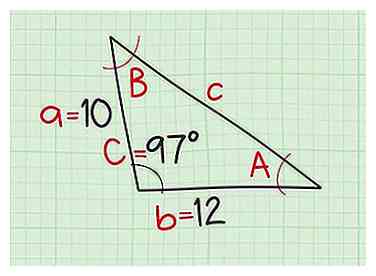 2 Kijk naar je driehoek en wijs variabele letters toe aan zijn componenten. De eerste zijde waarvan u weet dat deze moet worden geëtiketteerd eenen de tegenoverliggende hoek is EEN. De tweede zijde waarvan u weet dat deze moet worden geëtiketteerd b; de hoek tegenovergesteld is B. De hoek die u kent, moet worden gemarkeerd Cen de derde kant, degene die je moet oplossen om de omtrek van de driehoek te vinden, is kant c.
2 Kijk naar je driehoek en wijs variabele letters toe aan zijn componenten. De eerste zijde waarvan u weet dat deze moet worden geëtiketteerd eenen de tegenoverliggende hoek is EEN. De tweede zijde waarvan u weet dat deze moet worden geëtiketteerd b; de hoek tegenovergesteld is B. De hoek die u kent, moet worden gemarkeerd Cen de derde kant, degene die je moet oplossen om de omtrek van de driehoek te vinden, is kant c. - Stel u bijvoorbeeld een driehoek voor met lengtes 10 en 12 op de zijkant en een hoek daartussen van 97 °. We zullen variabelen als volgt toewijzen: a = 10, b = 12, C = 97 °.
-
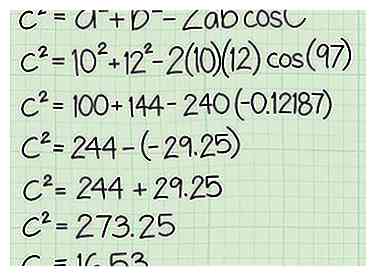 3 Steek uw gegevens in de vergelijking en los op voor c. U moet eerst de vierkanten van a en b vinden en ze samenvoegen. Zoek dan de cosinus van C met behulp van de cos functie op uw rekenmachine, of een online cosinuscalculator.[5] Vermenigvuldigen cos(C) door 2ab en trek het product af van de som van een2 + b2. Het resultaat is c2. Zoek de vierkantswortel van deze waarde en je hebt de lengte van de zijde c. Onze voorbeelddriehoek gebruiken:
3 Steek uw gegevens in de vergelijking en los op voor c. U moet eerst de vierkanten van a en b vinden en ze samenvoegen. Zoek dan de cosinus van C met behulp van de cos functie op uw rekenmachine, of een online cosinuscalculator.[5] Vermenigvuldigen cos(C) door 2ab en trek het product af van de som van een2 + b2. Het resultaat is c2. Zoek de vierkantswortel van deze waarde en je hebt de lengte van de zijde c. Onze voorbeelddriehoek gebruiken: - c2 = 102 + 122 - 2 × 10 × 12 × cos(97).
- c2 = 100 + 144 - (240 × -0.12187) (Rond de cosinus tot op 5 decimalen.)
- c2 = 244 - (-29.25)
- c2 = 244 + 29.25 (Draag het minteken door wanneer cos(C) is negatief!)
- c2 = 273.25
- c = 16.53
-
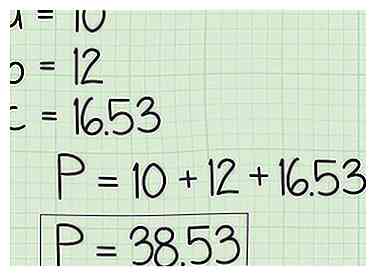 4 Gebruik kantlengte c om de omtrek van de driehoek te vinden. Denk aan die perimeter P = a + b + c, dus alles wat je hoeft te doen is de lengte toevoegen die je net hebt berekend voor de zijkant c naar de waarden waar je al voor had een en b.
4 Gebruik kantlengte c om de omtrek van de driehoek te vinden. Denk aan die perimeter P = a + b + c, dus alles wat je hoeft te doen is de lengte toevoegen die je net hebt berekend voor de zijkant c naar de waarden waar je al voor had een en b. - In ons voorbeeld: 10 + 12 + 16.53 = 38.53, de omtrek van onze driehoek!
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
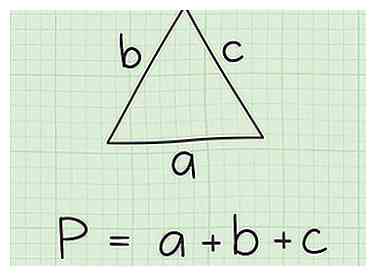 1 Denk aan de formule voor het vinden van de omtrek van een driehoek. Voor een driehoek met zijden een, b en c, de omtrek P is gedefinieerd als: P = a + b + c.
1 Denk aan de formule voor het vinden van de omtrek van een driehoek. Voor een driehoek met zijden een, b en c, de omtrek P is gedefinieerd als: P = a + b + c.  2 Kijk naar je driehoek en bepaal de lengte van de drie zijden. In dit voorbeeld de lengte van de zijkant een = 5, de lengte van de zijkant b = 5en de lengte van de zijkant c = 5.
2 Kijk naar je driehoek en bepaal de lengte van de drie zijden. In dit voorbeeld de lengte van de zijkant een = 5, de lengte van de zijkant b = 5en de lengte van de zijkant c = 5. 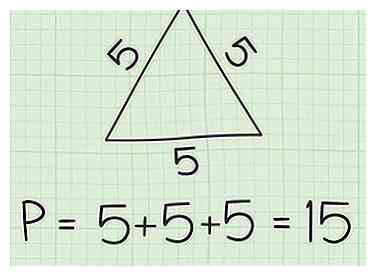 3 Voeg de drie zijlengtes samen toe om de omtrek te vinden. In dit voorbeeld 5 + 5 + 5 = 15. daarom P = 15.
3 Voeg de drie zijlengtes samen toe om de omtrek te vinden. In dit voorbeeld 5 + 5 + 5 = 15. daarom P = 15.  4 Vergeet niet om de eenheden op te nemen in uw definitieve antwoord. Als de zijden van de driehoek in centimeters worden gemeten, moet uw antwoord ook in centimeters zijn. Als de zijden worden gemeten in termen van een variabele zoals x, moet uw antwoord ook in termen van x zijn.
4 Vergeet niet om de eenheden op te nemen in uw definitieve antwoord. Als de zijden van de driehoek in centimeters worden gemeten, moet uw antwoord ook in centimeters zijn. Als de zijden worden gemeten in termen van een variabele zoals x, moet uw antwoord ook in termen van x zijn.  1 Onthoud wat een rechthoekige driehoek is. Een rechterdriehoek is een driehoek die één rechtse (90 graden) hoek heeft. De zijde van de driehoek tegenover de rechte hoek is altijd de langste zijde en wordt de hypotenusa genoemd. Juiste driehoeken verschijnen vaak bij wiskundetests en gelukkig is er een zeer handige formule om de lengte van onbekende zijden te vinden!
1 Onthoud wat een rechthoekige driehoek is. Een rechterdriehoek is een driehoek die één rechtse (90 graden) hoek heeft. De zijde van de driehoek tegenover de rechte hoek is altijd de langste zijde en wordt de hypotenusa genoemd. Juiste driehoeken verschijnen vaak bij wiskundetests en gelukkig is er een zeer handige formule om de lengte van onbekende zijden te vinden! 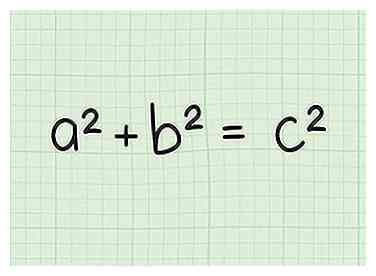 2 Denk aan de stelling van Pythagoras. De stelling van Pythagoras vertelt ons dat voor elke rechthoekige driehoek met zijden van lengte a en b en hypotenusa van lengte c, een2 + b2 = c2.[2]
2 Denk aan de stelling van Pythagoras. De stelling van Pythagoras vertelt ons dat voor elke rechthoekige driehoek met zijden van lengte a en b en hypotenusa van lengte c, een2 + b2 = c2.[2]  3 Kijk naar je driehoek en label de zijkanten "a", "b" en "c". Vergeet niet dat de langste zijde van de driehoek de hypotenusa wordt genoemd. Het staat tegenover de juiste hoek en moet worden geëtiketteerd c. Label de twee korte zijden een en b. Het maakt niet echt uit wat is wat, de wiskunde zal hetzelfde blijken!
3 Kijk naar je driehoek en label de zijkanten "a", "b" en "c". Vergeet niet dat de langste zijde van de driehoek de hypotenusa wordt genoemd. Het staat tegenover de juiste hoek en moet worden geëtiketteerd c. Label de twee korte zijden een en b. Het maakt niet echt uit wat is wat, de wiskunde zal hetzelfde blijken!  4 Voer de lengtes in die je kent in de stelling van Pythagoras. Onthoudt dat een2 + b2 = c2. Vervang de lengtes langs de zijkant voor de corresponderende letters in de vergelijking.
4 Voer de lengtes in die je kent in de stelling van Pythagoras. Onthoudt dat een2 + b2 = c2. Vervang de lengtes langs de zijkant voor de corresponderende letters in de vergelijking. 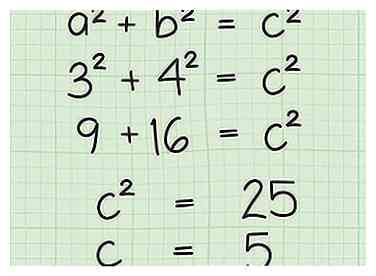 5 Los de vergelijking op om de lengte van de ontbrekende zijde te vinden. U zult eerst de bekende lengtes van de zijden moeten verdelen, wat betekent dat elke waarde afzonderlijk moet worden vermenigvuldigd (bijvoorbeeld 32 = 3 * 3 = 9). Als u op zoek bent naar de hypotenusa, voegt u eenvoudig de twee waarden bij elkaar en vindt u de vierkantswortel van dit getal om de lengte te vinden. Als het een lengte van de zijkant is die u mist, moet u een beetje gemakkelijk aftrekken doen en vervolgens de vierkantswortel nemen om uw zijde te vergroten.
5 Los de vergelijking op om de lengte van de ontbrekende zijde te vinden. U zult eerst de bekende lengtes van de zijden moeten verdelen, wat betekent dat elke waarde afzonderlijk moet worden vermenigvuldigd (bijvoorbeeld 32 = 3 * 3 = 9). Als u op zoek bent naar de hypotenusa, voegt u eenvoudig de twee waarden bij elkaar en vindt u de vierkantswortel van dit getal om de lengte te vinden. Als het een lengte van de zijkant is die u mist, moet u een beetje gemakkelijk aftrekken doen en vervolgens de vierkantswortel nemen om uw zijde te vergroten. 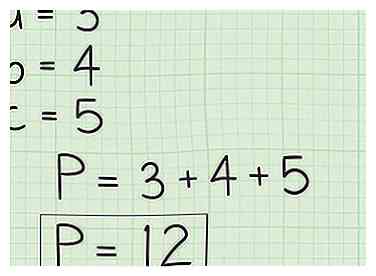 6 Tel de lengten van de drie zijlengten bij elkaar op om de omtrek te vinden. Bedenk dat de omtrek P = a + b + c. Nu dat je de lengte van zijden kent een, b en c, u hoeft alleen de lengtes bij elkaar op te tellen om de omtrek te vinden.
6 Tel de lengten van de drie zijlengten bij elkaar op om de omtrek te vinden. Bedenk dat de omtrek P = a + b + c. Nu dat je de lengte van zijden kent een, b en c, u hoeft alleen de lengtes bij elkaar op te tellen om de omtrek te vinden. 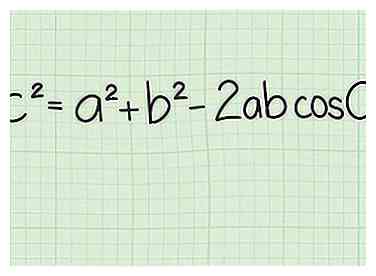 1 Leer de wet van Cosinus. De Law of Cosines stelt je in staat elke driehoek op te lossen als je twee lengtes opzij kent en de hoek ertussen meet. Het werkt op elke driehoek en is een zeer nuttige formule. De wet van Cosinus stelt dat voor elke driehoek met zijden een, b, en c, met tegenovergestelde hoeken EEN, B, en C: c2 = a2 + b2 - 2ab cos(C).[3][4]
1 Leer de wet van Cosinus. De Law of Cosines stelt je in staat elke driehoek op te lossen als je twee lengtes opzij kent en de hoek ertussen meet. Het werkt op elke driehoek en is een zeer nuttige formule. De wet van Cosinus stelt dat voor elke driehoek met zijden een, b, en c, met tegenovergestelde hoeken EEN, B, en C: c2 = a2 + b2 - 2ab cos(C).[3][4]  2 Kijk naar je driehoek en wijs variabele letters toe aan zijn componenten. De eerste zijde waarvan u weet dat deze moet worden geëtiketteerd eenen de tegenoverliggende hoek is EEN. De tweede zijde waarvan u weet dat deze moet worden geëtiketteerd b; de hoek tegenovergesteld is B. De hoek die u kent, moet worden gemarkeerd Cen de derde kant, degene die je moet oplossen om de omtrek van de driehoek te vinden, is kant c.
2 Kijk naar je driehoek en wijs variabele letters toe aan zijn componenten. De eerste zijde waarvan u weet dat deze moet worden geëtiketteerd eenen de tegenoverliggende hoek is EEN. De tweede zijde waarvan u weet dat deze moet worden geëtiketteerd b; de hoek tegenovergesteld is B. De hoek die u kent, moet worden gemarkeerd Cen de derde kant, degene die je moet oplossen om de omtrek van de driehoek te vinden, is kant c. 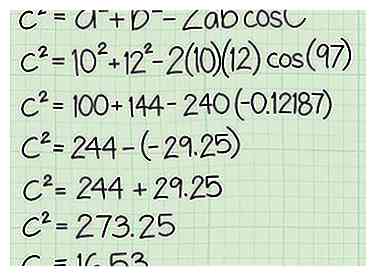 3 Steek uw gegevens in de vergelijking en los op voor c. U moet eerst de vierkanten van a en b vinden en ze samenvoegen. Zoek dan de cosinus van C met behulp van de cos functie op uw rekenmachine, of een online cosinuscalculator.[5] Vermenigvuldigen cos(C) door 2ab en trek het product af van de som van een2 + b2. Het resultaat is c2. Zoek de vierkantswortel van deze waarde en je hebt de lengte van de zijde c. Onze voorbeelddriehoek gebruiken:
3 Steek uw gegevens in de vergelijking en los op voor c. U moet eerst de vierkanten van a en b vinden en ze samenvoegen. Zoek dan de cosinus van C met behulp van de cos functie op uw rekenmachine, of een online cosinuscalculator.[5] Vermenigvuldigen cos(C) door 2ab en trek het product af van de som van een2 + b2. Het resultaat is c2. Zoek de vierkantswortel van deze waarde en je hebt de lengte van de zijde c. Onze voorbeelddriehoek gebruiken: 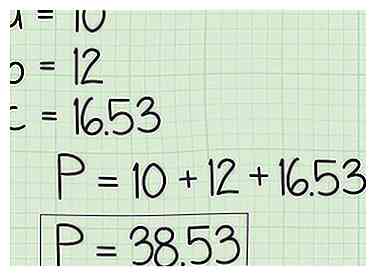 4 Gebruik kantlengte c om de omtrek van de driehoek te vinden. Denk aan die perimeter P = a + b + c, dus alles wat je hoeft te doen is de lengte toevoegen die je net hebt berekend voor de zijkant c naar de waarden waar je al voor had een en b.
4 Gebruik kantlengte c om de omtrek van de driehoek te vinden. Denk aan die perimeter P = a + b + c, dus alles wat je hoeft te doen is de lengte toevoegen die je net hebt berekend voor de zijkant c naar de waarden waar je al voor had een en b.