Het oppervlak van een vorm is de som van het oppervlak van alle vlakken. Om het gebied van een cilinder te vinden, moet je het gebied van de basissen vinden en dat toevoegen aan het gedeelte van de buitenmuur. De formule voor het vinden van het oppervlak van een cilinder is A = 2πr2 + 2πrh.
Deel een van de drie:
Het oppervlak van de cirkels berekenen (2 x (π x r2))
-
 1 Visualiseer de boven- en onderkant van een cilinder. Een blik soep is de vorm van een cilinder. Als je erover nadenkt, heeft het blik een boven- en onderkant die hetzelfde zijn. Beide uiteinden hebben de vorm van een cirkel. De eerste stap om het oppervlak van uw cilinder te vinden, is om het oppervlak van deze ronde uiteinden te vinden.[1]
1 Visualiseer de boven- en onderkant van een cilinder. Een blik soep is de vorm van een cilinder. Als je erover nadenkt, heeft het blik een boven- en onderkant die hetzelfde zijn. Beide uiteinden hebben de vorm van een cirkel. De eerste stap om het oppervlak van uw cilinder te vinden, is om het oppervlak van deze ronde uiteinden te vinden.[1] -
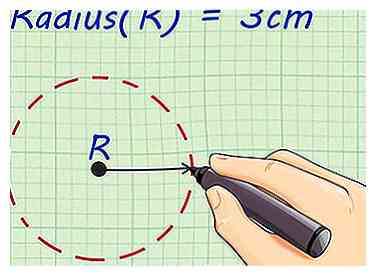 2 Zoek de straal van je cilinder. De straal is de afstand van het middelpunt van een cirkel tot de buitenrand van de cirkel. Straal wordt afgekort als "r." De straal van uw cilinder is gelijk aan de straal van de bovenste en onderste cirkels. In dit voorbeeld is de straal van de basis 3 centimeter (1,2 in).[2]
2 Zoek de straal van je cilinder. De straal is de afstand van het middelpunt van een cirkel tot de buitenrand van de cirkel. Straal wordt afgekort als "r." De straal van uw cilinder is gelijk aan de straal van de bovenste en onderste cirkels. In dit voorbeeld is de straal van de basis 3 centimeter (1,2 in).[2] - Als u een woordprobleem oplost, kan de straal worden opgegeven. De diameter kan ook worden gegeven, dat is de afstand van de ene kant van de cirkel naar de andere, die door het middelpunt gaat. De straal is precies de helft van de diameter.
- U kunt de straal meten met een liniaal als u op zoek bent naar het oppervlak van een echte cilinder.
-
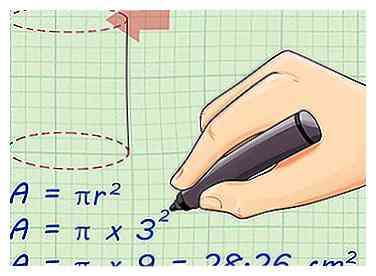 3 Bereken het oppervlak van de bovenste cirkel. Het oppervlak van een cirkel is gelijk aan het aantal pi (~ 3,14) maal de straal van de cirkel in het kwadraat. De vergelijking is geschreven als π x r2. Dit is hetzelfde als zeggen π x r x r.
3 Bereken het oppervlak van de bovenste cirkel. Het oppervlak van een cirkel is gelijk aan het aantal pi (~ 3,14) maal de straal van de cirkel in het kwadraat. De vergelijking is geschreven als π x r2. Dit is hetzelfde als zeggen π x r x r. - Om het gebied van de basis te vinden, steekt u gewoon de straal van 3 centimeter (1.2 in) in de vergelijking om het gebied van een cirkel te vinden: A = πr2. Hier is hoe je het doet:[3]
- A = πr2
- A = π x 32
- A = π x 9 = 28,26 cm2
-
 4 Doe het nog een keer voor de cirkel aan de andere kant. Nu dat je hebt opgelost voor het gebied van één basis, moet je rekening houden met het gebied van het tweede honk. Je kunt dezelfde stappen volgen als bij het eerste honk, of je kunt herkennen dat de honken identiek zijn. Je kunt overslaan met de gebiedsvergelijking een tweede keer gebruiken voor het tweede honk als je dit begrijpt.[4]
4 Doe het nog een keer voor de cirkel aan de andere kant. Nu dat je hebt opgelost voor het gebied van één basis, moet je rekening houden met het gebied van het tweede honk. Je kunt dezelfde stappen volgen als bij het eerste honk, of je kunt herkennen dat de honken identiek zijn. Je kunt overslaan met de gebiedsvergelijking een tweede keer gebruiken voor het tweede honk als je dit begrijpt.[4]
Tweede deel van de drie:
Het oppervlak van de rand berekenen (2π x r x h)
-
 1 Visualiseer de buitenrand van een cilinder. Wanneer u een cilindrisch soepblik visualiseert, ziet u een boven- en onderbodem. De bases zijn met elkaar verbonden door een "muur" van blik. De straal van de muur is hetzelfde als de straal van de basis, maar in tegenstelling tot de basis heeft de muur een hoogte.[5]
1 Visualiseer de buitenrand van een cilinder. Wanneer u een cilindrisch soepblik visualiseert, ziet u een boven- en onderbodem. De bases zijn met elkaar verbonden door een "muur" van blik. De straal van de muur is hetzelfde als de straal van de basis, maar in tegenstelling tot de basis heeft de muur een hoogte.[5] -
 2 Zoek de omtrek van een van de cirkels. U moet de omtrek vinden om het oppervlak van de buitenrand te vinden (ook bekend als lateraal oppervlak). Om de omtrek te krijgen, vermenigvuldigt u eenvoudig de straal met 2π. De omtrek is dus te vinden door 3 centimeter (1.2 in) te vermenigvuldigen met 2π. 3 centimeter (1,2 in) x 2π = 18,84 centimeter (7,4 inch).[6]
2 Zoek de omtrek van een van de cirkels. U moet de omtrek vinden om het oppervlak van de buitenrand te vinden (ook bekend als lateraal oppervlak). Om de omtrek te krijgen, vermenigvuldigt u eenvoudig de straal met 2π. De omtrek is dus te vinden door 3 centimeter (1.2 in) te vermenigvuldigen met 2π. 3 centimeter (1,2 in) x 2π = 18,84 centimeter (7,4 inch).[6] -
 3 Vermenigvuldig de omtrek van de cirkel met de hoogte van de cilinder. Dit geeft je het buitenste oppervlak van de rand. Vermenigvuldig de omtrek, 18,84 centimeter (7,4 in), bij de hoogte, 5 centimeter (2,0 in). 18,84 centimeter (7,4 inch) x 5 centimeter (2,0 inch) = 94,2 cm2.[7]
3 Vermenigvuldig de omtrek van de cirkel met de hoogte van de cilinder. Dit geeft je het buitenste oppervlak van de rand. Vermenigvuldig de omtrek, 18,84 centimeter (7,4 in), bij de hoogte, 5 centimeter (2,0 in). 18,84 centimeter (7,4 inch) x 5 centimeter (2,0 inch) = 94,2 cm2.[7]
Derde deel van de drie:
Het samenvoegen ((2) x (π x r2)) + (2π x r x h)
-
 1 Visualiseer de hele cilinder. Eerst visualiseerde je hoe de boven- en onderkant van de basis en opgelost voor het gebied op die oppervlakken. Vervolgens dacht je aan de muur die zich uitstrekt tussen die basissen en die is opgelost voor die ruimte. Denk deze keer aan het blik als geheel, en je lost het hele oppervlak op.[8]
1 Visualiseer de hele cilinder. Eerst visualiseerde je hoe de boven- en onderkant van de basis en opgelost voor het gebied op die oppervlakken. Vervolgens dacht je aan de muur die zich uitstrekt tussen die basissen en die is opgelost voor die ruimte. Denk deze keer aan het blik als geheel, en je lost het hele oppervlak op.[8] -
 2 Verdubbel het gebied van één basis. Simpelweg het vorige resultaat vermenigvuldigen, 28,26 cm2, door 2 om het gebied van beide bases te krijgen. 28,26 x 2 = 56,52 cm2. Dit geeft je het gebied van beide bases.[9]
2 Verdubbel het gebied van één basis. Simpelweg het vorige resultaat vermenigvuldigen, 28,26 cm2, door 2 om het gebied van beide bases te krijgen. 28,26 x 2 = 56,52 cm2. Dit geeft je het gebied van beide bases.[9] -
 3 Voeg het gebied van de muur en het basisgebied toe. Nadat u het gebied van de twee bases en het buitenoppervlak hebt toegevoegd, zult u het oppervlak van de cilinder hebben gevonden. Het enige wat je hoeft te doen is 56,52 cm toevoegen2het gebied van beide bases en de buitenoppervlakte, 94,2 cm2. 56,52 cm2 + 94,2 cm2 = 150.72 cm2. Het oppervlak met een cilinder met een hoogte van 5 centimeter (2.0 in) en een cirkelvormige basis met een straal van 3 centimeter (1.2 in) is 150.72 cm2.[10]
3 Voeg het gebied van de muur en het basisgebied toe. Nadat u het gebied van de twee bases en het buitenoppervlak hebt toegevoegd, zult u het oppervlak van de cilinder hebben gevonden. Het enige wat je hoeft te doen is 56,52 cm toevoegen2het gebied van beide bases en de buitenoppervlakte, 94,2 cm2. 56,52 cm2 + 94,2 cm2 = 150.72 cm2. Het oppervlak met een cilinder met een hoogte van 5 centimeter (2.0 in) en een cirkelvormige basis met een straal van 3 centimeter (1.2 in) is 150.72 cm2.[10]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Visualiseer de boven- en onderkant van een cilinder. Een blik soep is de vorm van een cilinder. Als je erover nadenkt, heeft het blik een boven- en onderkant die hetzelfde zijn. Beide uiteinden hebben de vorm van een cirkel. De eerste stap om het oppervlak van uw cilinder te vinden, is om het oppervlak van deze ronde uiteinden te vinden.[1]
1 Visualiseer de boven- en onderkant van een cilinder. Een blik soep is de vorm van een cilinder. Als je erover nadenkt, heeft het blik een boven- en onderkant die hetzelfde zijn. Beide uiteinden hebben de vorm van een cirkel. De eerste stap om het oppervlak van uw cilinder te vinden, is om het oppervlak van deze ronde uiteinden te vinden.[1]  2 Zoek de straal van je cilinder. De straal is de afstand van het middelpunt van een cirkel tot de buitenrand van de cirkel. Straal wordt afgekort als "r." De straal van uw cilinder is gelijk aan de straal van de bovenste en onderste cirkels. In dit voorbeeld is de straal van de basis 3 centimeter (1,2 in).[2]
2 Zoek de straal van je cilinder. De straal is de afstand van het middelpunt van een cirkel tot de buitenrand van de cirkel. Straal wordt afgekort als "r." De straal van uw cilinder is gelijk aan de straal van de bovenste en onderste cirkels. In dit voorbeeld is de straal van de basis 3 centimeter (1,2 in).[2]  3 Bereken het oppervlak van de bovenste cirkel. Het oppervlak van een cirkel is gelijk aan het aantal pi (~ 3,14) maal de straal van de cirkel in het kwadraat. De vergelijking is geschreven als π x r2. Dit is hetzelfde als zeggen π x r x r.
3 Bereken het oppervlak van de bovenste cirkel. Het oppervlak van een cirkel is gelijk aan het aantal pi (~ 3,14) maal de straal van de cirkel in het kwadraat. De vergelijking is geschreven als π x r2. Dit is hetzelfde als zeggen π x r x r.  4 Doe het nog een keer voor de cirkel aan de andere kant. Nu dat je hebt opgelost voor het gebied van één basis, moet je rekening houden met het gebied van het tweede honk. Je kunt dezelfde stappen volgen als bij het eerste honk, of je kunt herkennen dat de honken identiek zijn. Je kunt overslaan met de gebiedsvergelijking een tweede keer gebruiken voor het tweede honk als je dit begrijpt.[4]
4 Doe het nog een keer voor de cirkel aan de andere kant. Nu dat je hebt opgelost voor het gebied van één basis, moet je rekening houden met het gebied van het tweede honk. Je kunt dezelfde stappen volgen als bij het eerste honk, of je kunt herkennen dat de honken identiek zijn. Je kunt overslaan met de gebiedsvergelijking een tweede keer gebruiken voor het tweede honk als je dit begrijpt.[4]  1 Visualiseer de buitenrand van een cilinder. Wanneer u een cilindrisch soepblik visualiseert, ziet u een boven- en onderbodem. De bases zijn met elkaar verbonden door een "muur" van blik. De straal van de muur is hetzelfde als de straal van de basis, maar in tegenstelling tot de basis heeft de muur een hoogte.[5]
1 Visualiseer de buitenrand van een cilinder. Wanneer u een cilindrisch soepblik visualiseert, ziet u een boven- en onderbodem. De bases zijn met elkaar verbonden door een "muur" van blik. De straal van de muur is hetzelfde als de straal van de basis, maar in tegenstelling tot de basis heeft de muur een hoogte.[5]  2 Zoek de omtrek van een van de cirkels. U moet de omtrek vinden om het oppervlak van de buitenrand te vinden (ook bekend als lateraal oppervlak). Om de omtrek te krijgen, vermenigvuldigt u eenvoudig de straal met 2π. De omtrek is dus te vinden door 3 centimeter (1.2 in) te vermenigvuldigen met 2π. 3 centimeter (1,2 in) x 2π = 18,84 centimeter (7,4 inch).[6]
2 Zoek de omtrek van een van de cirkels. U moet de omtrek vinden om het oppervlak van de buitenrand te vinden (ook bekend als lateraal oppervlak). Om de omtrek te krijgen, vermenigvuldigt u eenvoudig de straal met 2π. De omtrek is dus te vinden door 3 centimeter (1.2 in) te vermenigvuldigen met 2π. 3 centimeter (1,2 in) x 2π = 18,84 centimeter (7,4 inch).[6]  3 Vermenigvuldig de omtrek van de cirkel met de hoogte van de cilinder. Dit geeft je het buitenste oppervlak van de rand. Vermenigvuldig de omtrek, 18,84 centimeter (7,4 in), bij de hoogte, 5 centimeter (2,0 in). 18,84 centimeter (7,4 inch) x 5 centimeter (2,0 inch) = 94,2 cm2.[7]
3 Vermenigvuldig de omtrek van de cirkel met de hoogte van de cilinder. Dit geeft je het buitenste oppervlak van de rand. Vermenigvuldig de omtrek, 18,84 centimeter (7,4 in), bij de hoogte, 5 centimeter (2,0 in). 18,84 centimeter (7,4 inch) x 5 centimeter (2,0 inch) = 94,2 cm2.[7]  1 Visualiseer de hele cilinder. Eerst visualiseerde je hoe de boven- en onderkant van de basis en opgelost voor het gebied op die oppervlakken. Vervolgens dacht je aan de muur die zich uitstrekt tussen die basissen en die is opgelost voor die ruimte. Denk deze keer aan het blik als geheel, en je lost het hele oppervlak op.[8]
1 Visualiseer de hele cilinder. Eerst visualiseerde je hoe de boven- en onderkant van de basis en opgelost voor het gebied op die oppervlakken. Vervolgens dacht je aan de muur die zich uitstrekt tussen die basissen en die is opgelost voor die ruimte. Denk deze keer aan het blik als geheel, en je lost het hele oppervlak op.[8]  2 Verdubbel het gebied van één basis. Simpelweg het vorige resultaat vermenigvuldigen, 28,26 cm2, door 2 om het gebied van beide bases te krijgen. 28,26 x 2 = 56,52 cm2. Dit geeft je het gebied van beide bases.[9]
2 Verdubbel het gebied van één basis. Simpelweg het vorige resultaat vermenigvuldigen, 28,26 cm2, door 2 om het gebied van beide bases te krijgen. 28,26 x 2 = 56,52 cm2. Dit geeft je het gebied van beide bases.[9]  3 Voeg het gebied van de muur en het basisgebied toe. Nadat u het gebied van de twee bases en het buitenoppervlak hebt toegevoegd, zult u het oppervlak van de cilinder hebben gevonden. Het enige wat je hoeft te doen is 56,52 cm toevoegen2het gebied van beide bases en de buitenoppervlakte, 94,2 cm2. 56,52 cm2 + 94,2 cm2 = 150.72 cm2. Het oppervlak met een cilinder met een hoogte van 5 centimeter (2.0 in) en een cirkelvormige basis met een straal van 3 centimeter (1.2 in) is 150.72 cm2.[10]
3 Voeg het gebied van de muur en het basisgebied toe. Nadat u het gebied van de twee bases en het buitenoppervlak hebt toegevoegd, zult u het oppervlak van de cilinder hebben gevonden. Het enige wat je hoeft te doen is 56,52 cm toevoegen2het gebied van beide bases en de buitenoppervlakte, 94,2 cm2. 56,52 cm2 + 94,2 cm2 = 150.72 cm2. Het oppervlak met een cilinder met een hoogte van 5 centimeter (2.0 in) en een cirkelvormige basis met een straal van 3 centimeter (1.2 in) is 150.72 cm2.[10]