Hoe het oppervlaktegebied te vinden

Oppervlakte is de totale hoeveelheid ruimte die alle oppervlakken van een object innemen. Het is de som van het oppervlak van alle oppervlakken van dat object.^[1] Het vinden van het oppervlak van een driedimensionale vorm is redelijk eenvoudig, zolang u de juiste formule kent. Elke vorm heeft zijn eigen afzonderlijke formule, dus u moet eerst de vorm identificeren waarmee u werkt. Het onthouden van de oppervlakteformule voor verschillende objecten kan het maken van berekeningen in de toekomst eenvoudiger maken. Hier zijn enkele van de meest voorkomende vormen die u kunt tegenkomen.

Methode één van de zeven:
Kubus

1. 1 Definieer de formule voor het oppervlak van een kubus. Een kubus heeft zes identieke vierkante zijden. Omdat zowel de lengte als de breedte van een vierkant gelijk zijn, is het gebied van een vierkant een², waar een is de lengte van een zijde. Omdat er 6 identieke zijden van een kubus zijn, kunt u het oppervlak eenvoudigweg vermenigvuldigen met het gebied van één zijde. 6. De formule voor oppervlakte (SA) van een kubus is SA = 6a², waar een is de lengte van één kant.^[2]
   • De oppervlakte-eenheden hebben een lengte-eenheid in het kwadraat: in², cm², m², enz.
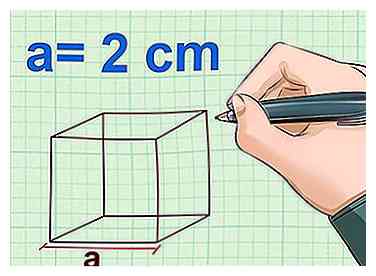2. 2 Meet de lengte van één zijde. Elke zijde of rand van een kubus moet per definitie in lengte gelijk zijn aan de andere, dus u hoeft slechts één kant te meten. Gebruik een liniaal om de lengte van de zijkant te meten. Besteed aandacht aan de eenheden die u gebruikt.
   • Markeer deze meting als een.
   • Voorbeeld: a = 2 cm
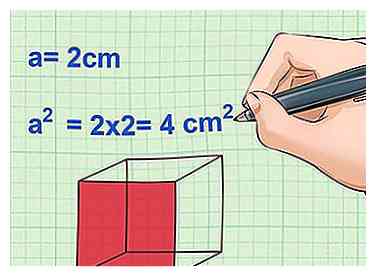3. 3 Vier je maat voor een. Vier de gemeten afmeting voor de lengte van de rand. Een meting in het vierkant plaatsen betekent het alleen vermenigvuldigen. Wanneer u deze formules voor het eerst leert, kan het handig zijn om deze te schrijven SA = 6 * a * a.
   • Merk op dat deze stap het gebied van één kant van de kubus berekent.
   • Voorbeeld: a = 2 cm
   • een² = 2 x 2 = 4 cm²
4. 4 Vermenigvuldig dit product met zes. Vergeet niet dat een kubus zes identieke zijden heeft. Nu dat u het gebied van één kant hebt, moet u het met zes vermenigvuldigen om rekening te houden met alle zes zijden.
   • Met deze stap wordt de berekening voor het oppervlak van de kubus voltooid.
   • Voorbeeld: een² = 4 cm²
   • Oppervlakte = 6 x a² = 6 x 4 = 24 cm²

Methode twee van zeven:
Rechthoekig prisma

1. 1 Definieer de formule voor het oppervlak van een rechthoekig prisma. Net als een kubus heeft een rechthoekig prisma zes zijden, maar in tegenstelling tot een kubus zijn de zijkanten niet identiek. In een rechthoekig prisma zijn alleen tegenoverliggende zijden gelijk.^[3] Daarom moet het oppervlak van een rechthoekig prisma rekening houden met de verschillende lengtes die de formule vormen SA = 2ab + 2bc + 2ac.
   • Voor deze formule, een is gelijk aan de breedte van het prisma, b is gelijk aan de hoogte, en c is gelijk aan de lengte.
   • Als u de formule doorbreekt, kunt u zien dat u eenvoudig alle gebieden van elk vlak van het object optelt.
   • De oppervlakte-eenheden hebben een lengte-eenheid in het kwadraat: in², cm², m², enz.
2. 2 Meet de lengte, hoogte en breedte van elke zijde. Alle drie de metingen kunnen variëren, dus alle drie moeten afzonderlijk worden genomen. Gebruik een liniaal om elke zijde te meten en op te schrijven. Gebruik dezelfde eenheden voor elke meting.
   • Meet de lengte van de basis om de lengte van het prisma te bepalen en wijs dit toe aan c.
   • Voorbeeld: c = 5 cm
   • Meet de breedte van de basis om de breedte van het prisma te bepalen en wijs dit toe aan een.
   • Voorbeeld: a = 2 cm
   • Meet de hoogte van de zijkant om de hoogte van het prisma te bepalen en wijs dit toe aan b.
   • Voorbeeld: b = 3 cm
3. 3 Bereken het gebied van een van de zijden van het prisma en vermenigvuldig het vervolgens met twee. Denk eraan, er zijn 6 vlakken van een rechthoekig prisma, maar tegenoverliggende zijden zijn identiek. Vermenigvuldig de lengte en hoogte, of c en een om het gebied van één gezicht te vinden. Neem deze meting en vermenigvuldig deze met twee om rekening te houden met de tegenovergestelde identieke zijde.^[4]
   • Voorbeeld: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 cm²
4. 4 Zoek het gebied van de andere kant van het prisma en vermenigvuldig dit met twee. Net als bij het eerste paar vlakken, vermenigvuldig de breedte en hoogte, of een en b om het gebied van een ander gezicht van het prisma te vinden. Vermenigvuldig deze meting met twee om rekening te houden met de tegenovergestelde identieke zijden.^[5]
   • Voorbeeld: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 cm²
5. 5 Bereken het gebied van de uiteinden van het prisma en vermenigvuldig dit met twee. De laatste twee gezichten van het prisma zijn de uiteinden. Vermenigvuldig de lengte en breedte, of c en b om hun gebied te vinden. Vermenigvuldig deze meting met twee om rekening te houden met beide zijden.^[6]
   • Voorbeeld: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 cm²
6. 6 Voeg de drie afzonderlijke metingen samen toe. Omdat het oppervlak het totale oppervlak van alle vlakken van een object is, is de laatste stap om alle afzonderlijk berekende gebieden bij elkaar te voegen. Voeg de oppervlaktematen voor alle zijden samen toe om het totale oppervlak te vinden.^[7]
   • Voorbeeld: Oppervlakte = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 cm².

Methode Three of Seven:
Driehoekig Prisma

1. 1 Definieer de oppervlakte-formule voor een driehoekig prisma. Een driehoekig prisma heeft twee identieke driehoekige zijden en drie rechthoekige vlakken. Om het oppervlak te vinden, moet u het gebied van alle zijden berekenen en ze samen optellen. Het oppervlak van een driehoekig prisma is SA = 2A + PH, waarbij A het gebied van de driehoekige basis is, P de omtrek van de driehoekige basis en h de hoogte van het prisma.^[8]
   • Voor deze formule, EEN is het gebied van een driehoek dat is A = 1 / 2bh waar b is de basis van de driehoek en h is de hoogte.
   • P is gewoon de omtrek van de driehoek die wordt berekend door alle drie zijden van de driehoek bij elkaar te voegen.
   • De oppervlakte-eenheden hebben een lengte-eenheid in het kwadraat: in², cm², m², enz.
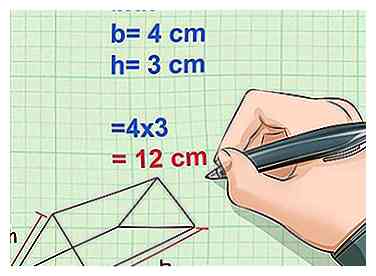2. 2 Bereken het gebied van het driehoekige vlak en vermenigvuldig dit met twee. Het gebied van een driehoek is ¹/₂b * h waar b de basis van de driehoek is en h de hoogte. Omdat er twee identieke driehoeken zijn, kunnen we de formule vermenigvuldigen met twee. Dit maakt de berekening voor beide gezichten eenvoudig, b * h.^[9]
   • De basis, b, is gelijk aan de lengte van de onderkant van de driehoek.
   • Voorbeeld: b = 4 cm
   • De hoogte, h, van de driehoekige basis is de afstand tussen de onderkant en de top.
   • Voorbeeld: h = 3 cm
   • Oppervlakte van de ene driehoek vermenigvuldigd met 2 = 2 (1/2) b * h = b * h = 4 * 3 = 12 cm
3. 3 Meet elke kant van de driehoek en de hoogte van het prisma. Om de oppervlakteberekening te voltooien, moet u de lengte van elke zijde van de driehoek en de hoogte van het prisma kennen. De hoogte is de afstand tussen de twee driehoekige vlakken.
   • Voorbeeld: H = 5 cm
   • De drie zijden verwijzen naar de drie zijden van de driehoekige basis.
   • Voorbeeld: S1 = 2 cm, S2 = 4 cm, S3 = 6 cm
4. 4 Bepaal de omtrek van de driehoek. De omtrek van de driehoek kan eenvoudig worden berekend door alle gemeten zijden bij elkaar op te tellen: S1 + S2 + S3.
   • Voorbeeld: P = S1 + S2 + S3 = 2 + 4 + 6 = 12 cm
5. 5 Vermenigvuldig de omtrek van de basis met de hoogte van het prisma. Denk eraan, de hoogte van het prisma is de afstand tussen de twee driehoekige basissen. Met andere woorden, vermenigvuldig P door H.
   • Voorbeeld: P x H = 12 x 5 = 60 cm²
6. 6 Voeg de twee afzonderlijke metingen samen toe. U moet de twee metingen van de vorige twee stappen samen toevoegen om het oppervlak van de driehoekige prisma te berekenen.^[10]
   • Voorbeeld: 2A + PH = 12 + 60 = 72 cm².

Methode vier van zeven:
Gebied

1. 1 Definieer de oppervlaktegebiedformule voor een bol. Een bol heeft een gebogen oppervlak en daarom moet het oppervlak de wiskundige constante, pi, gebruiken. Het oppervlak van een bol wordt gegeven door de vergelijking SA = 4π * r².^[11]
   • Voor deze formule, r is gelijk aan de straal van de bol. Pi, of π, moet worden geschat op 3,14.
   • De oppervlakte-eenheden hebben een lengte-eenheid in het kwadraat: in², cm², m², enz.
2. 2 Meet de straal van de bol. De straal van de bol is de helft van de diameter, of de helft van de afstand van de ene kant van het middelpunt van de bol tot de andere.^[12]
   • Voorbeeld: r = 3 cm
3. 3 Plein de straal. Om een ​​getal vierkant te maken, vermenigvuldigt u het eenvoudig zelf. Vermenigvuldig de meting voor r alleen. Onthoud dat deze formule kan worden herschreven als SA = 4π * r * r.^[13]
   • Voorbeeld: r² = r x r = 3 x 3 = 9 cm²
4. 4 Vermenigvuldig de gekwadrateerde straal met een benadering van pi. Pi is een constante die de verhouding van de omtrek van een cirkel tot zijn diameter weergeeft.^[14] Het is een irrationeel getal met veel decimalen. Het wordt vaak benaderd als 3,14. Vermenigvuldig de gekwadrateerde straal met π of 3.14 om het gebied van één cirkelvormig gedeelte van de bol te vinden.^[15]
   • Voorbeeld: π * r² = 3,14 x 9 = 28,26 cm²
5. 5 Vermenigvuldig dit product met vier. Om de berekening te voltooien, vermenigvuldigt u met 4. Zoek het oppervlak van de bol door het platte ronde gebied te vermenigvuldigen met vier.^[16]
   • Voorbeeld: 4π r *² = 4 x 28,26 = 113,04 cm²

Methode Five of Seven:
Cilinder

1. 1 Definieer de oppervlakte-formule voor een cilinder. Een cilinder heeft twee cirkelvormige uiteinden die een afgerond oppervlak omsluiten. De formule voor het oppervlak van een cilinder is SA = 2π * r² + 2π * rh, waar r is gelijk aan de straal van de cirkelvormige basis en h is gelijk aan de hoogte van de cilinder. Ronde pi of π uit tot 3.14.^[17]
   • 2π r *² vertegenwoordigt het oppervlaktegebied van de twee cirkelvormige uiteinden terwijl 2πrh het oppervlaktegebied is van de kolom die de twee uiteinden verbindt.
   • De oppervlakte-eenheden hebben een lengte-eenheid in het kwadraat: in², cm², m², enz.
2. 2 Meet de straal en hoogte van de cilinder. De straal van een cirkel is de helft van de diameter, of de helft van de afstand van de ene kant van het midden van de cirkel naar de andere.^[18] De hoogte is de totale afstand van de cilinder van begin tot eind. Gebruik een liniaal om deze metingen uit te voeren en op te schrijven.
   • Voorbeeld: r = 3 cm
   • Voorbeeld: h = 5 cm
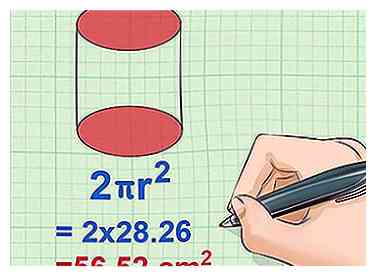3. 3 Zoek het gebied van de basis en vermenigvuldig dit met twee. Om het gebied van de basis te vinden, gebruikt u eenvoudig de formule voor het gebied van de cirkel of π * r². Om de berekening te voltooien, moet u de straal vierkant maken en vermenigvuldigen met pi. Vermenigvuldig met twee om rekening te houden met de tweede identieke cirkel aan het andere uiteinde van de cilinder.^[19]
   • Voorbeeld: basisgebied = π * r² = 3,14 x 3 x 3 = 28,26 cm²
   • Voorbeeld: 2π r *² = 2 x 28,26 = 56,52 cm²
4. 4 Bereken het oppervlak van de cilinder zelf met behulp van 2π * rh. Dit is de formule om het oppervlak van een buis te berekenen. De buis is de ruimte tussen de twee cirkelvormige uiteinden van de cilinder. Vermenigvuldig de straal met twee, pien de hoogte.^[20]
   • Voorbeeld: 2π * rh = 2 x 3,14 x 3 x 5 = 94,2 cm²
5. 5 Voeg de twee afzonderlijke metingen samen toe. Voeg het oppervlak van de twee cirkels toe aan het oppervlak van de ruimte tussen de twee cirkels om het totale oppervlak van de cilinder te berekenen.Merk op dat als je deze twee stukken bij elkaar optelt, je de originele formule kunt herkennen: SA = 2π * r² + 2π * rh.^[21]
   • Voorbeeld: 2π r *² + 2π * rh = 56,52 + 94,2 = 150,72 cm²

Methode Six of Seven:
Vierkante piramide

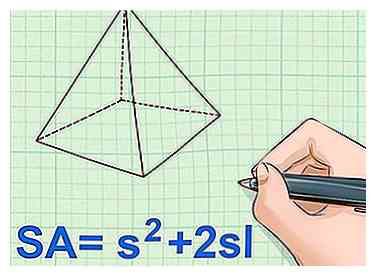1. 1 Definieer de oppervlakte-formule voor een vierkante piramide. Een vierkante piramide heeft een vierkante basis en vier driehoekige zijden. Denk eraan, het vierkant is de lengte van een vierkantje. Het gebied van een driehoek is 1 / 2sl (kant van de driehoek maal de lengte of hoogte van de driehoek). Omdat er vier driehoeken zijn, moet je om de totale oppervlakte te vinden, met vier vermenigvuldigen. Als al deze vlakken bij elkaar worden opgeteld, krijg je de vergelijking van het oppervlak voor een vierkante piramide: SA = s² + 2sl.^[22]
   • Voor deze vergelijking, s verwijst naar de lengte van elke zijde van de vierkante basis en l verwijst naar de schuine hoogte van elke driehoekige zijde.
   • De oppervlakte-eenheden hebben een lengte-eenheid in het kwadraat: in², cm², m², enz.
2. 2 Meet de schuine hoogte en de basiszijde. De schuine hoogte, l, is de hoogte van een van de driehoekige zijden. Het is de afstand tussen de basis tot de top van de piramide gemeten langs een vlakke zijde. De basiskant, s, is de lengte van één zijde van de vierkante basis. Omdat de basis vierkant is, is deze meting voor alle kanten gelijk. Gebruik een liniaal om elke meting uit te voeren.^[23]
   • Voorbeeld: l = 3 cm
   • Voorbeeld: s = 1 cm
3. 3 Zoek het gebied van de vierkante basis. Het gebied van een vierkante basis kan worden berekend door de lengte van een zijde te verkanten of te vermenigvuldigen s alleen.^[24]
   • Voorbeeld: s² = s x s = 1 x 1 = 1 cm²
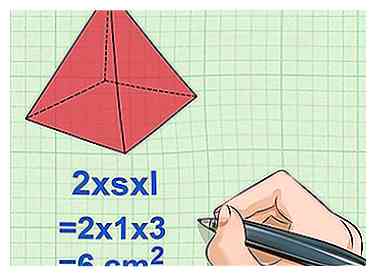4. 4 Bereken het totale gebied van de vier driehoekige vlakken. Het tweede deel van de vergelijking betreft het oppervlak van de resterende vier driehoekige zijden. Gebruik de formule 2ls om te vermenigvuldigen s door l en twee. Als je dat doet, kun je het gebied van elke kant vinden.^[25]
   • Voorbeeld: 2 x s x l = 2 x 1 x 3 = 6 cm²
5. 5 Voeg de twee afzonderlijke gebieden samen toe. Voeg het totale gebied van de zijden toe aan het gebied van de basis om het totale oppervlak te berekenen.^[26]
   • Voorbeeld: s² + 2sl = 1 + 6 = 7 cm²

Methode Seven of Seven:
Kegel

1. 1 Definieer de oppervlakte-formule voor een kegel. Een kegel heeft een ronde basis en een afgerond oppervlak dat uitloopt in een punt. Om het oppervlak te vinden, moet je het gebied van de cirkelvormige basis en het oppervlak van de kegel berekenen en deze twee samenvoegen. De formule voor het oppervlak van een kegel is: SA = π * r² + π * rl, waar r is de straal van de cirkelvormige basis, l is de schuine hoogte van de kegel en π is de wiskundige constante pi (3.14).^[27]
   • De oppervlakte-eenheden hebben een lengte-eenheid in het kwadraat: in², cm², m², enz.
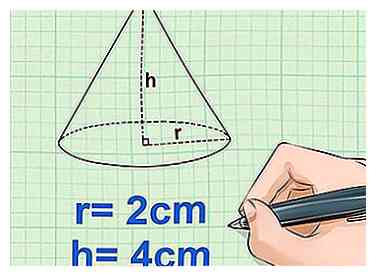2. 2 Meet de straal en hoogte van de kegel. De straal is de afstand van het midden van de cirkelvormige basis tot de zijkant van de basis. De hoogte is de afstand van het midden van de basis tot de hoogste top van de kegel, gemeten door het midden van de kegel.^[28]
   • Voorbeeld: r = 2 cm
   • Voorbeeld: h = 4 cm
3. 3 Bereken de schuine hoogte (l) van de kegel. Omdat de schuine hoogte eigenlijk de hypotenusa van een driehoek is, moet je de stelling van Pythagoras gebruiken om het te berekenen. Gebruik het herschikte formulier, l = √ (r² + h²), waar r is de straal en h is de hoogte van de kegel. ^[29]
   • Voorbeeld: l = √ (r² + h²) = √ (2 x 2 + 4 x 4) = √ (4 + 16) = √ (20) = 4,47 cm
4. 4 Bepaal het gebied van de cirkelvormige basis. Het gebied van de basis wordt berekend met de formule π * r². Na het meten van de straal, haak het vierkant (vermenigvuldig het zelf) en vermenigvuldig dat product met pi.^[30]
   • Voorbeeld: π * r² = 3,14 x 2 x 2 = 12,56 cm²
5. 5 Bereken het oppervlak van de bovenkant van de kegel. Met behulp van de formule π * rl, waar r is de straal van de cirkel en l is de eerder berekende schuine hoogte, u kunt het oppervlak van het bovenste gedeelte van de kegel vinden.^[31]
   • Voorbeeld: π * rl = 3,14 x 2 x 4,47 = 28,07 cm
6. 6 Voeg twee gebieden bij elkaar om het totale oppervlak te vinden. Bereken het uiteindelijke oppervlak van je kegel door het gebied van de cirkelvormige basis toe te voegen aan de berekening uit de vorige stap.^[32]
   • Voorbeeld: π * r² + π * rl = 12.56 + 28.07 = 40.63 cm²