Het oppervlak van een kegel is de som van het zijoppervlak en het basisoppervlak. Als u de straal van de basis en de schuine hoogte van de kegel kent, kunt u het totale oppervlak gemakkelijk vinden met behulp van een standaardformule. Soms hebt u echter de straal en een andere maat, zoals de hoogte of het volume van de kegel. In deze gevallen kunt u de stelling van Pythagoras en de volumeformule gebruiken om de schuine hoogte en daarmee het oppervlak van de kegel af te leiden.
Methode één van de drie:
Als u de straal en de schuine hoogte kent
-
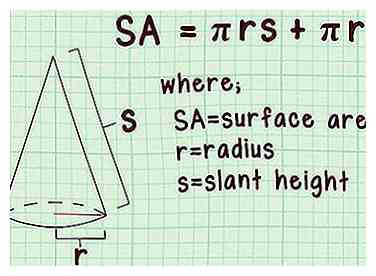 1 Stel de formule in voor het oppervlak van de kegel. De formule is , waar is gelijk aan het oppervlak van de kegel, is gelijk aan de lengte van de straal van de basis van de kegel, en is gelijk aan de schuine hoogte van de kegel.[1]
1 Stel de formule in voor het oppervlak van de kegel. De formule is , waar is gelijk aan het oppervlak van de kegel, is gelijk aan de lengte van de straal van de basis van de kegel, en is gelijk aan de schuine hoogte van de kegel.[1] - Het totale oppervlak van een kegel is gelijk aan de som van het zijoppervlak () en het basisgebied (), omdat de basis van een kegel een cirkel is.
- De schuine hoogte is de diagonale afstand van de topvertex van de kegel tot de rand van de basis.[2]
- Zorg ervoor dat je de "hoogte" niet verwart met de "hoogte", die de loodrechte afstand is tussen de topvertex en de basis.[3]
-
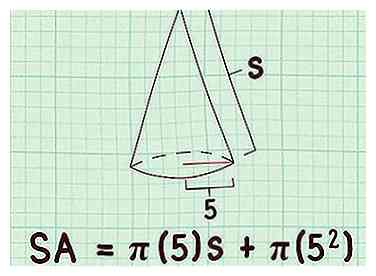 2 Steek de waarde van de straal in de formule. Deze lengte zou moeten worden gegeven, of je zou in staat moeten zijn om het te meten. Zorg ervoor dat je beide vervangt variabelen in de formule.
2 Steek de waarde van de straal in de formule. Deze lengte zou moeten worden gegeven, of je zou in staat moeten zijn om het te meten. Zorg ervoor dat je beide vervangt variabelen in de formule. - Als de straal van de basis van een kegel bijvoorbeeld 5 cm is, ziet uw formule er als volgt uit: .
-
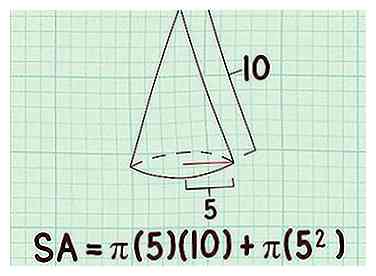 3 Steek de waarde van de schuine hoogte in de formule. Deze lengte zou moeten worden gegeven, of je zou in staat moeten zijn om het te meten.
3 Steek de waarde van de schuine hoogte in de formule. Deze lengte zou moeten worden gegeven, of je zou in staat moeten zijn om het te meten. - Als de schuine hoogte van een kegel bijvoorbeeld 10 cm is, ziet uw formule er als volgt uit: .
-
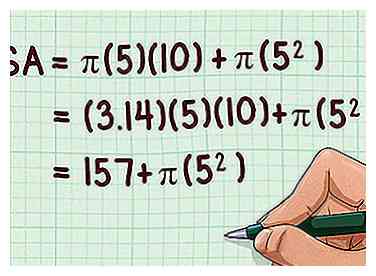 4 Bereken het zijoppervlak van de kegel (). Om dit te doen, vermenigvuldigt u de straal, de schuine hoogte en . Als u geen rekenmachine gebruikt, gebruik dan 3.14 als de waarde van .
4 Bereken het zijoppervlak van de kegel (). Om dit te doen, vermenigvuldigt u de straal, de schuine hoogte en . Als u geen rekenmachine gebruikt, gebruik dan 3.14 als de waarde van . - Bijvoorbeeld:
- Bijvoorbeeld:
-
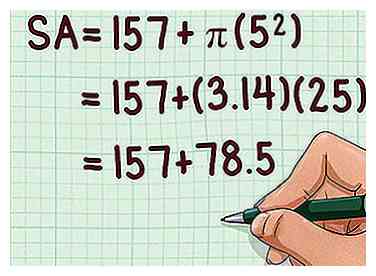 5 Bereken het oppervlak van de basis van de kegel (). Om dit te doen, vierkant de straal van de basis, dan vermenigvuldigen met . Als u geen rekenmachine gebruikt, gebruik dan 3.14 als de waarde van .
5 Bereken het oppervlak van de basis van de kegel (). Om dit te doen, vierkant de straal van de basis, dan vermenigvuldigen met . Als u geen rekenmachine gebruikt, gebruik dan 3.14 als de waarde van . - Bijvoorbeeld:
- Bijvoorbeeld:
-
 6 Voeg de laterale oppervlakte en het basisgebied van de kegel toe. Dit geeft je het totale oppervlak van de kegel, in vierkante eenheden.
6 Voeg de laterale oppervlakte en het basisgebied van de kegel toe. Dit geeft je het totale oppervlak van de kegel, in vierkante eenheden. - Bijvoorbeeld:
Het oppervlak van een kegel met een straal van 5 cm en een schuine hoogte van 10 cm is dus 235,5 vierkante centimeter.
- Bijvoorbeeld:
Methode twee van drie:
Als u de straal en de verticale hoogte kent
-
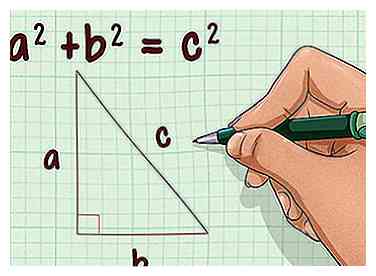
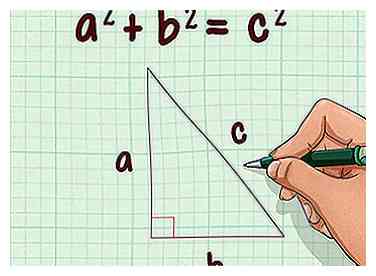 1 Stel de formule voor de stelling van Pythagoras op. De formule is , waar en gelijk aan de lengte van de zijkant van een rechthoekige driehoek, en is gelijk aan de lengte van de hypotenusa (de zijde tegenover de rechte hoek).[4]
1 Stel de formule voor de stelling van Pythagoras op. De formule is , waar en gelijk aan de lengte van de zijkant van een rechthoekige driehoek, en is gelijk aan de lengte van de hypotenusa (de zijde tegenover de rechte hoek).[4] - Zorg ervoor dat u de hoogte van de kegel niet verwart met de schuine hoogte, die de diagonale afstand is van de tophoek van de kegel tot de rand van de basis.[5]
- De hoogte is de loodrechte afstand tussen de topvertex en de basis.[6]
-
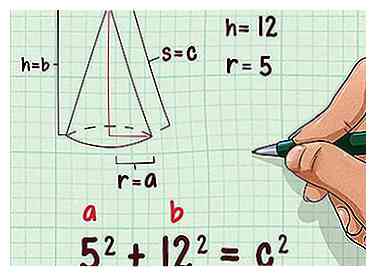 2 Steek de lengte van de straal en hoogte in de formule. Je gebruikt de straal en hoogte van de kegel als de twee zijden van een rechthoekige driehoek. Vervang de straal voor de variabele en de hoogte voor de variabele .
2 Steek de lengte van de straal en hoogte in de formule. Je gebruikt de straal en hoogte van de kegel als de twee zijden van een rechthoekige driehoek. Vervang de straal voor de variabele en de hoogte voor de variabele . - Als de straal van een kegel bijvoorbeeld 5 cm is en de hoogte 12 cm, ziet uw formule er als volgt uit: .
-
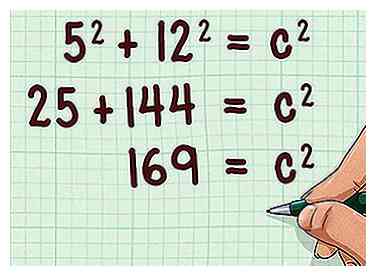 3 Vier de lengten van de straal en hoogte en voeg vervolgens toe. Onthoud dat het kwadrateren van een getal betekent het alleen vermenigvuldigen.
3 Vier de lengten van de straal en hoogte en voeg vervolgens toe. Onthoud dat het kwadrateren van een getal betekent het alleen vermenigvuldigen. - Bijvoorbeeld:
- Bijvoorbeeld:
-
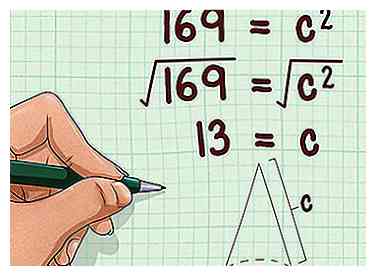 4 Neem de vierkantswortel van elke kant van de vergelijking. Dit geeft je de lengte van de schuine zijde van de rechthoekige driehoek, die gelijk is aan de schuine hoogte van de kegel.[7]
4 Neem de vierkantswortel van elke kant van de vergelijking. Dit geeft je de lengte van de schuine zijde van de rechthoekige driehoek, die gelijk is aan de schuine hoogte van de kegel.[7] - Bijvoorbeeld:
Dus de schuine hoogte van de kegel is 13 cm.
- Bijvoorbeeld:
-
 5 Stel de formule in voor het oppervlak van de kegel. De formule is , waar is gelijk aan het oppervlak van de kegel, is gelijk aan de lengte van de straal van de basis van de kegel, en is gelijk aan de schuine hoogte van de kegel.[8]
5 Stel de formule in voor het oppervlak van de kegel. De formule is , waar is gelijk aan het oppervlak van de kegel, is gelijk aan de lengte van de straal van de basis van de kegel, en is gelijk aan de schuine hoogte van de kegel.[8] - Het totale oppervlak van een kegel is gelijk aan de som van het zijoppervlak () en het basisgebied (, omdat de basis van een kegel een cirkel is).
-
 6 Sluit alle bekende waarden in de formule in. De straal moet worden gegeven en u hebt de schuine hoogte al berekend. Zorg ervoor dat u de schuine hoogte gebruikt in de formule voor het oppervlak, niet de (loodrechte) hoogte. Als u geen rekenmachine gebruikt, gebruik dan 3,14 voor
6 Sluit alle bekende waarden in de formule in. De straal moet worden gegeven en u hebt de schuine hoogte al berekend. Zorg ervoor dat u de schuine hoogte gebruikt in de formule voor het oppervlak, niet de (loodrechte) hoogte. Als u geen rekenmachine gebruikt, gebruik dan 3,14 voor - Voor een kegel met een straal van 5 cm en een schuine hoogte van 13 cm ziet uw formule er bijvoorbeeld als volgt uit: .
-
 7 Vermenigvuldigen om het laterale gebied en het basisgebied te vinden. Voeg deze producten vervolgens samen toe. De som geeft u het totale oppervlak van de kegel in vierkante eenheden.
7 Vermenigvuldigen om het laterale gebied en het basisgebied te vinden. Voeg deze producten vervolgens samen toe. De som geeft u het totale oppervlak van de kegel in vierkante eenheden. - Bijvoorbeeld:
Het oppervlak van een kegel met een straal van 5 cm en een hoogte van 12 cm is dus 282,6 vierkante centimeter.
- Bijvoorbeeld:
Methode drie van drie:
Als u de straal en het volume kent
-
 1 Stel de formule in voor het volume van een kegel. De formule is , waar is gelijk aan het volume van de kegel, is gelijk aan de straal van de basis van de kegel, en is gelijk aan de loodrechte hoogte van de kegel.[9]
1 Stel de formule in voor het volume van een kegel. De formule is , waar is gelijk aan het volume van de kegel, is gelijk aan de straal van de basis van de kegel, en is gelijk aan de loodrechte hoogte van de kegel.[9] - Zorg ervoor dat u de hoogte van de kegel niet verwart met de schuine hoogte, die de diagonale afstand is van de tophoek van de kegel tot de rand van de basis.[10]
- De hoogte is de loodrechte afstand tussen de topvertex en de basis.[11]
-
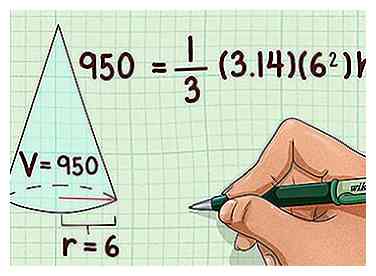 2 Sluit de bekende waarden aan in de formule. U moet het volume en de lengte van de straal weten. Zo niet, dan kunt u deze methode niet gebruiken. Als u geen rekenmachine gebruikt, gebruik dan 3,14 voor .
2 Sluit de bekende waarden aan in de formule. U moet het volume en de lengte van de straal weten. Zo niet, dan kunt u deze methode niet gebruiken. Als u geen rekenmachine gebruikt, gebruik dan 3,14 voor . - Als u bijvoorbeeld weet dat een kegel een volume van 950 kubieke centimeter en een straal van 6 centimeter heeft, ziet uw formule er als volgt uit: .
-
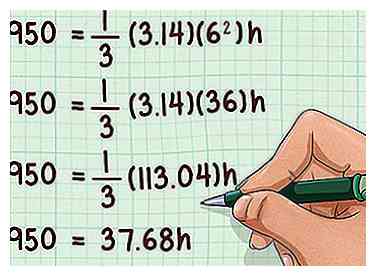 3 Voltooi de vermenigvuldiging. Maak eerst de straal vierkant en vermenigvuldig die waarde met . Vermenigvuldig dat product vervolgens met . Dit geeft je de coëfficiënt voor de variabel.
3 Voltooi de vermenigvuldiging. Maak eerst de straal vierkant en vermenigvuldig die waarde met . Vermenigvuldig dat product vervolgens met . Dit geeft je de coëfficiënt voor de variabel. - Bijvoorbeeld:
- Bijvoorbeeld:
-
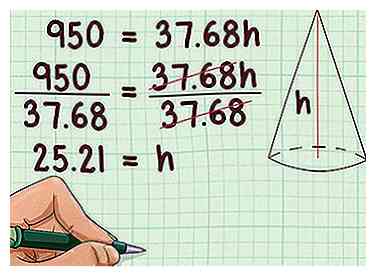 4 Verdeel elke zijde door de coëfficiënt. Dit geeft je de waarde van , dat is de loodrechte hoogte van de kegel. U hebt deze informatie nodig om de schuine hoogte van de kegel te vinden, wat nodig is om te weten wanneer u oplost voor het oppervlak.
4 Verdeel elke zijde door de coëfficiënt. Dit geeft je de waarde van , dat is de loodrechte hoogte van de kegel. U hebt deze informatie nodig om de schuine hoogte van de kegel te vinden, wat nodig is om te weten wanneer u oplost voor het oppervlak. - Bijvoorbeeld:
Dus de hoogte van de kegel is 25,21 cm.
- Bijvoorbeeld:
-
 5 Stel de formule voor de stelling van Pythagoras op. De formule is , waar en gelijk aan de lengte van de zijkant van een rechthoekige driehoek, en is gelijk aan de lengte van de hypotenusa (de zijde tegenover de rechte hoek).[12]
5 Stel de formule voor de stelling van Pythagoras op. De formule is , waar en gelijk aan de lengte van de zijkant van een rechthoekige driehoek, en is gelijk aan de lengte van de hypotenusa (de zijde tegenover de rechte hoek).[12] -
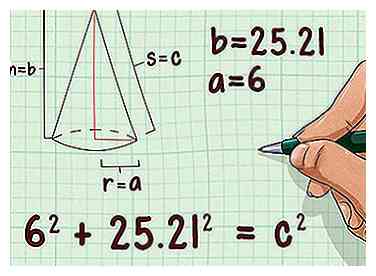 6 Steek de lengte van de straal en hoogte in de formule. Je gebruikt de straal en hoogte van de kegel als de twee zijden van een rechthoekige driehoek. Vervang de straal voor de variabele en de hoogte voor de variabele
6 Steek de lengte van de straal en hoogte in de formule. Je gebruikt de straal en hoogte van de kegel als de twee zijden van een rechthoekige driehoek. Vervang de straal voor de variabele en de hoogte voor de variabele - Als de straal van een kegel bijvoorbeeld 6 cm is en de hoogte 25,21 cm, ziet uw formule er als volgt uit: .
-
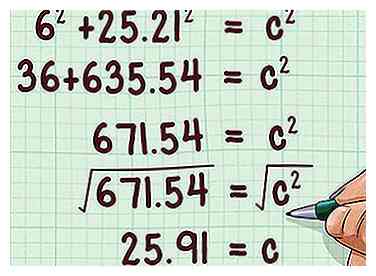 7 Oplossen voor . Dit geeft je de lengte van de schuine zijde van de rechthoekige driehoek, wat ook de schuine hoogte van de kegel is.
7 Oplossen voor . Dit geeft je de lengte van de schuine zijde van de rechthoekige driehoek, wat ook de schuine hoogte van de kegel is. - Bijvoorbeeld:
Dus de schuine hoogte van de kegel is 25,91 cm.
- Bijvoorbeeld:
-
 8 Stel de formule in voor het oppervlak van de kegel. De formule is , waar is gelijk aan het oppervlak van de kegel, is gelijk aan de lengte van de straal van de basis van de kegel, en is gelijk aan de schuine hoogte van de kegel.[13]
8 Stel de formule in voor het oppervlak van de kegel. De formule is , waar is gelijk aan het oppervlak van de kegel, is gelijk aan de lengte van de straal van de basis van de kegel, en is gelijk aan de schuine hoogte van de kegel.[13] - Het totale oppervlak van een kegel is gelijk aan de som van het zijoppervlak () en het basisgebied (, omdat de basis van een kegel een cirkel is).
-
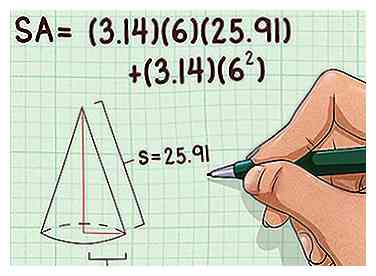 9 Sluit alle bekende waarden in de formule in. Zorg ervoor dat u de schuine hoogte gebruikt in de formule voor het oppervlak, niet de (loodrechte) hoogte. Als u geen rekenmachine gebruikt, gebruik dan 3,14 voor
9 Sluit alle bekende waarden in de formule in. Zorg ervoor dat u de schuine hoogte gebruikt in de formule voor het oppervlak, niet de (loodrechte) hoogte. Als u geen rekenmachine gebruikt, gebruik dan 3,14 voor - Voor een kegel met een straal van 6 cm en een schuine hoogte van 25,91 cm ziet uw formule er bijvoorbeeld als volgt uit: .
-
 10 Vermenigvuldigen om het laterale gebied en het basisgebied te vinden. Voeg deze producten vervolgens samen toe. De som geeft u het totale oppervlak van de kegel in vierkante eenheden.
10 Vermenigvuldigen om het laterale gebied en het basisgebied te vinden. Voeg deze producten vervolgens samen toe. De som geeft u het totale oppervlak van de kegel in vierkante eenheden. - Bijvoorbeeld:
Het oppervlak van een kegel met een straal van 6 centimeter en een volume van 950 kubieke centimeter is dus 601,18 vierkante centimeter.
- Bijvoorbeeld:
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Stel de formule in voor het oppervlak van de kegel. De formule is
1 Stel de formule in voor het oppervlak van de kegel. De formule is  2 Steek de waarde van de straal in de formule. Deze lengte zou moeten worden gegeven, of je zou in staat moeten zijn om het te meten. Zorg ervoor dat je beide vervangt
2 Steek de waarde van de straal in de formule. Deze lengte zou moeten worden gegeven, of je zou in staat moeten zijn om het te meten. Zorg ervoor dat je beide vervangt  3 Steek de waarde van de schuine hoogte in de formule. Deze lengte zou moeten worden gegeven, of je zou in staat moeten zijn om het te meten.
3 Steek de waarde van de schuine hoogte in de formule. Deze lengte zou moeten worden gegeven, of je zou in staat moeten zijn om het te meten. 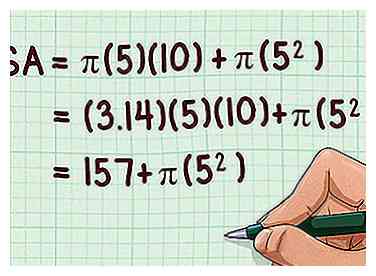 4 Bereken het zijoppervlak van de kegel (
4 Bereken het zijoppervlak van de kegel (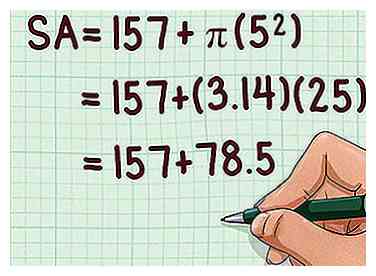 5 Bereken het oppervlak van de basis van de kegel (
5 Bereken het oppervlak van de basis van de kegel ( 6 Voeg de laterale oppervlakte en het basisgebied van de kegel toe. Dit geeft je het totale oppervlak van de kegel, in vierkante eenheden.
6 Voeg de laterale oppervlakte en het basisgebied van de kegel toe. Dit geeft je het totale oppervlak van de kegel, in vierkante eenheden. 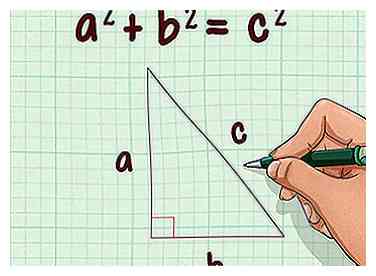 1 Stel de formule voor de stelling van Pythagoras op. De formule is
1 Stel de formule voor de stelling van Pythagoras op. De formule is 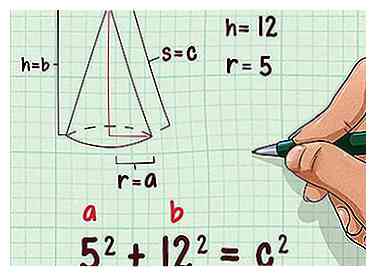 2 Steek de lengte van de straal en hoogte in de formule. Je gebruikt de straal en hoogte van de kegel als de twee zijden van een rechthoekige driehoek. Vervang de straal voor de variabele
2 Steek de lengte van de straal en hoogte in de formule. Je gebruikt de straal en hoogte van de kegel als de twee zijden van een rechthoekige driehoek. Vervang de straal voor de variabele 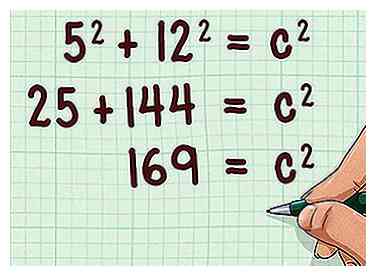 3 Vier de lengten van de straal en hoogte en voeg vervolgens toe. Onthoud dat het kwadrateren van een getal betekent het alleen vermenigvuldigen.
3 Vier de lengten van de straal en hoogte en voeg vervolgens toe. Onthoud dat het kwadrateren van een getal betekent het alleen vermenigvuldigen. 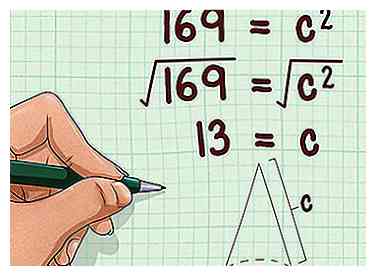 4 Neem de vierkantswortel van elke kant van de vergelijking. Dit geeft je de lengte van de schuine zijde van de rechthoekige driehoek, die gelijk is aan de schuine hoogte van de kegel.[7]
4 Neem de vierkantswortel van elke kant van de vergelijking. Dit geeft je de lengte van de schuine zijde van de rechthoekige driehoek, die gelijk is aan de schuine hoogte van de kegel.[7]  5 Stel de formule in voor het oppervlak van de kegel. De formule is
5 Stel de formule in voor het oppervlak van de kegel. De formule is  6 Sluit alle bekende waarden in de formule in. De straal moet worden gegeven en u hebt de schuine hoogte al berekend. Zorg ervoor dat u de schuine hoogte gebruikt in de formule voor het oppervlak, niet de (loodrechte) hoogte. Als u geen rekenmachine gebruikt, gebruik dan 3,14 voor
6 Sluit alle bekende waarden in de formule in. De straal moet worden gegeven en u hebt de schuine hoogte al berekend. Zorg ervoor dat u de schuine hoogte gebruikt in de formule voor het oppervlak, niet de (loodrechte) hoogte. Als u geen rekenmachine gebruikt, gebruik dan 3,14 voor  7 Vermenigvuldigen om het laterale gebied en het basisgebied te vinden. Voeg deze producten vervolgens samen toe. De som geeft u het totale oppervlak van de kegel in vierkante eenheden.
7 Vermenigvuldigen om het laterale gebied en het basisgebied te vinden. Voeg deze producten vervolgens samen toe. De som geeft u het totale oppervlak van de kegel in vierkante eenheden.  1 Stel de formule in voor het volume van een kegel. De formule is
1 Stel de formule in voor het volume van een kegel. De formule is 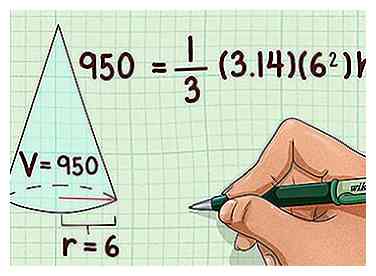 2 Sluit de bekende waarden aan in de formule. U moet het volume en de lengte van de straal weten. Zo niet, dan kunt u deze methode niet gebruiken. Als u geen rekenmachine gebruikt, gebruik dan 3,14 voor
2 Sluit de bekende waarden aan in de formule. U moet het volume en de lengte van de straal weten. Zo niet, dan kunt u deze methode niet gebruiken. Als u geen rekenmachine gebruikt, gebruik dan 3,14 voor 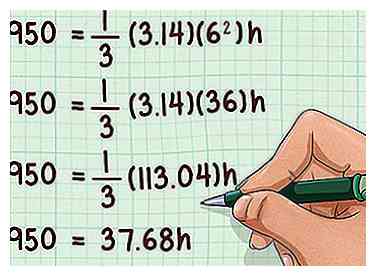 3 Voltooi de vermenigvuldiging. Maak eerst de straal vierkant en vermenigvuldig die waarde met
3 Voltooi de vermenigvuldiging. Maak eerst de straal vierkant en vermenigvuldig die waarde met 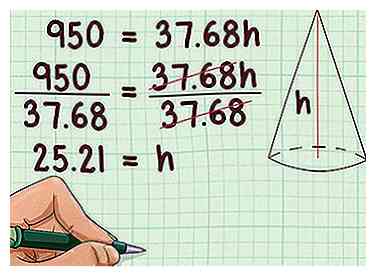 4 Verdeel elke zijde door de
4 Verdeel elke zijde door de  5 Stel de formule voor de stelling van Pythagoras op. De formule is
5 Stel de formule voor de stelling van Pythagoras op. De formule is 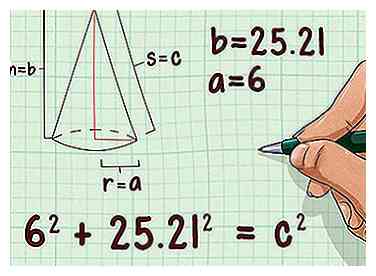 6 Steek de lengte van de straal en hoogte in de formule. Je gebruikt de straal en hoogte van de kegel als de twee zijden van een rechthoekige driehoek. Vervang de straal voor de variabele
6 Steek de lengte van de straal en hoogte in de formule. Je gebruikt de straal en hoogte van de kegel als de twee zijden van een rechthoekige driehoek. Vervang de straal voor de variabele 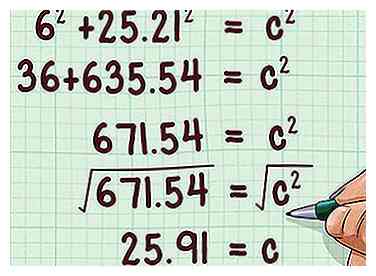 7 Oplossen voor
7 Oplossen voor  8 Stel de formule in voor het oppervlak van de kegel. De formule is
8 Stel de formule in voor het oppervlak van de kegel. De formule is 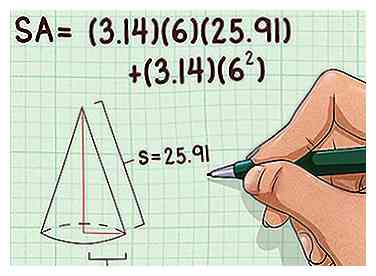 9 Sluit alle bekende waarden in de formule in. Zorg ervoor dat u de schuine hoogte gebruikt in de formule voor het oppervlak, niet de (loodrechte) hoogte. Als u geen rekenmachine gebruikt, gebruik dan 3,14 voor
9 Sluit alle bekende waarden in de formule in. Zorg ervoor dat u de schuine hoogte gebruikt in de formule voor het oppervlak, niet de (loodrechte) hoogte. Als u geen rekenmachine gebruikt, gebruik dan 3,14 voor  10 Vermenigvuldigen om het laterale gebied en het basisgebied te vinden. Voeg deze producten vervolgens samen toe. De som geeft u het totale oppervlak van de kegel in vierkante eenheden.
10 Vermenigvuldigen om het laterale gebied en het basisgebied te vinden. Voeg deze producten vervolgens samen toe. De som geeft u het totale oppervlak van de kegel in vierkante eenheden.