Het oppervlak van een object is het gecombineerde gebied van alle zijden op het oppervlak. Alle zes zijden van een kubus zijn congruent, dus om het oppervlak van een kubus te vinden, hoef je alleen maar het oppervlak van één kant van de kubus te vinden en het vervolgens met zes te vermenigvuldigen. Als u wilt weten hoe u het oppervlak van een kubus kunt vinden, volgt u deze stappen.

Methode één van de twee:
Het berekenen van het oppervlak dat de lengte van één kant kent

  1. 1 Begrijp dat het oppervlak van een kubus bestaat uit de gebieden van de zes vlakken. Omdat alle vlakken van een kubus congruent zijn, kunnen we gewoon het gebied van één vlak vinden en het met 6 vermenigvuldigen om de totale oppervlakte te krijgen. Het oppervlak kan worden gevonden door een eenvoudige formule te gebruiken: 6 x s2, waar "s" een kant van de kubus vertegenwoordigt.[1]
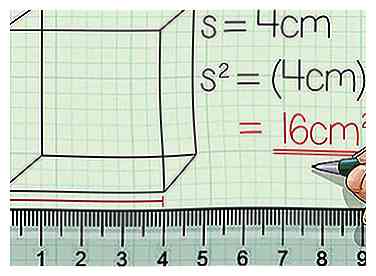  2. 2 Zoek het gebied van één kant van de kubus. Als u wilt zoeken naar de zijkant van de kubus, moet u 's' vinden, die de lengte van de zijkant van een kubus weergeeft en vervolgens zoeken naar2. Dit betekent echt dat je de lengte van de zijkant van de kubus vermenigvuldigd tot de breedte om het gebied te vinden - de lengte en breedte van de kant van een kubus zijn toevallig hetzelfde. Als een kant van de kubus of "s" gelijk is aan 4 centimeter (1,6 in), dan is het oppervlak van de zijkant van de kubus (4 cm)2of 16 cm2. Vergeet niet om uw antwoord in vierkante eenheden te vermelden.
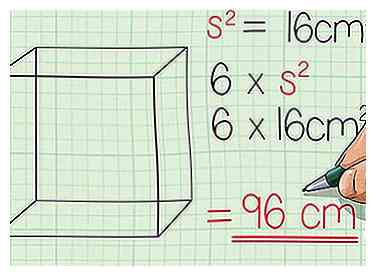  3. 3 Vermenigvuldig het gebied van de zijkant van de kubus met 6. Nu dat je het gebied van één kant van de kubus hebt gevonden, hoef je dit aantal alleen met 6 te vermenigvuldigen om het oppervlak te vinden. 16 cm2 x 6 = 96 cm2. Het oppervlak van de kubus is 96 cm2.

Methode twee van twee:
Het oppervlak berekenen Het volume kennen

  1. 1 Zoek het volume van de kubus. Laten we zeggen dat het volume van de kubus 125 cm is3.
  2. 2 Zoek de kubuswortel van het volume. Zoek naar de kubuswortel van het volume en zoek naar een getal dat kan worden gekubeerd om het volume te worden of gebruik uw rekenmachine. Het nummer zal niet altijd een geheel getal zijn. In dit geval is het getal 125 een perfecte kubus en is de wortel van de kubus 5, omdat 5 x 5 x 5 = 125. Dus "s" of een kant van de kubus is 5.
  3. 3 Steek dit antwoord in de formule om het oppervlak van een kubus te vinden. Nu je de lengte van één kant van een kubus kent, plug je hem gewoon in de formule om het oppervlak van een kubus te vinden: 6 x s2. Aangezien de lengte van één zijde 5 centimeter is, hoeft u deze maar zo in de formule te steken: 6 x (5 cm)2.
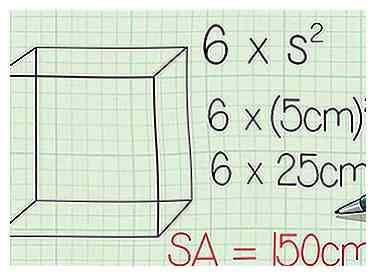  4. 4 Oplossen. Doe gewoon de wiskunde. 6 x (5 cm)2 = 6 x 25 cm2 = 150 centimeter (59.1 in) 2.