Het testen van hypothesen wordt gestuurd door statistische analyse. Statistische significantie wordt berekend met behulp van een p-waarde, die u de waarschijnlijkheid vertelt dat uw resultaat wordt waargenomen, aangezien een bepaalde verklaring (de nulhypothese) waar is.[1] Als deze p-waarde kleiner is dan het ingestelde significantieniveau (meestal 0,05), kan de onderzoeker aannemen dat de nulhypothese vals is en de alternatieve hypothese accepteren. Met behulp van een eenvoudige t-toets kunt u een p-waarde berekenen en de significantie bepalen tussen twee verschillende groepen van een gegevensset.
Deel een van de drie:
Uw experiment opzetten
-
 1 Definieer uw hypotheses. De eerste stap bij het beoordelen van statistische significantie is het definiëren van de vraag die u wilt beantwoorden en het aangeven van uw hypothese. De hypothese is een uitspraak over uw experimentele gegevens en de verschillen die zich in de populatie kunnen voordoen. Voor elk experiment is er zowel een nul als een alternatieve hypothese.[2] Over het algemeen zul je twee groepen vergelijken om te zien of ze hetzelfde of verschillend zijn.
1 Definieer uw hypotheses. De eerste stap bij het beoordelen van statistische significantie is het definiëren van de vraag die u wilt beantwoorden en het aangeven van uw hypothese. De hypothese is een uitspraak over uw experimentele gegevens en de verschillen die zich in de populatie kunnen voordoen. Voor elk experiment is er zowel een nul als een alternatieve hypothese.[2] Over het algemeen zul je twee groepen vergelijken om te zien of ze hetzelfde of verschillend zijn. - De nulhypothese (H.0) geeft in het algemeen aan dat er geen verschil is tussen uw twee gegevenssets. Bijvoorbeeld: studenten die het materiaal vóór de les lezen, krijgen geen betere eindcijfers.
- De alternatieve hypothese (H.een) is het tegenovergestelde van de nulhypothese en is de uitspraak die u probeert te ondersteunen met uw experimentele gegevens. Bijvoorbeeld: studenten die het materiaal vóór de les lezen, krijgen betere eindcijfers.
-
 2 Stel het significantieniveau in om te bepalen hoe ongewoon uw gegevens moeten zijn voordat deze als significant kan worden beschouwd. Het significantieniveau (ook wel alfa genoemd) is de drempel die u instelt om de significantie te bepalen. Als uw p-waarde kleiner is dan of gelijk is aan het ingestelde significantieniveau, worden de gegevens als statistisch significant beschouwd.[3]
2 Stel het significantieniveau in om te bepalen hoe ongewoon uw gegevens moeten zijn voordat deze als significant kan worden beschouwd. Het significantieniveau (ook wel alfa genoemd) is de drempel die u instelt om de significantie te bepalen. Als uw p-waarde kleiner is dan of gelijk is aan het ingestelde significantieniveau, worden de gegevens als statistisch significant beschouwd.[3] - Als algemene regel geldt dat het significantieniveau (of alpha) gewoonlijk wordt ingesteld op 0,05, wat betekent dat de kans om de verschillen waargenomen in uw gegevens per toeval te observeren slechts 5% is.
- Een hoger betrouwbaarheidsniveau (en dus een lagere p-waarde) betekent dat de resultaten significanter zijn.
- Als u meer vertrouwen in uw gegevens wilt, stelt u de p-waarde lager in op 0,01. Lagere p-waarden worden over het algemeen gebruikt bij de productie bij het detecteren van fouten in producten. Het is erg belangrijk om er zeker van te zijn dat elk onderdeel precies zal werken zoals het hoort.
- Voor de meeste hypothesegedreven experimenten is een significantieniveau van 0,05 acceptabel.
-
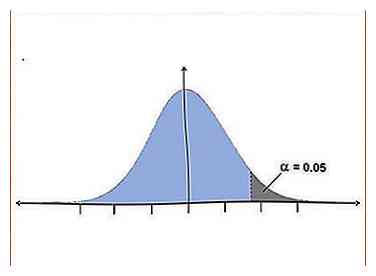 3 Besluit om een eenzijdige of tweezijdige toets te gebruiken. Een van de aannamen die een t-toets maakt, is dat uw gegevens normaal worden verspreid. Een normale gegevensverdeling vormt een belcurve waarbij het grootste deel van de monsters in het midden valt.[4] De t-toets is een wiskundige test om te zien of uw gegevens buiten de normale verdeling vallen, hetzij boven of onder, in de "uiteinden" van de curve.
3 Besluit om een eenzijdige of tweezijdige toets te gebruiken. Een van de aannamen die een t-toets maakt, is dat uw gegevens normaal worden verspreid. Een normale gegevensverdeling vormt een belcurve waarbij het grootste deel van de monsters in het midden valt.[4] De t-toets is een wiskundige test om te zien of uw gegevens buiten de normale verdeling vallen, hetzij boven of onder, in de "uiteinden" van de curve. - Een eenzijdige toets is krachtiger dan een tweezijdige toets, aangezien deze het potentieel van een relatie in één richting onderzoekt (zoals boven de controlegroep), terwijl een tweezijdige toets het potentieel van een relatie in beide onderzoekt. richtingen (zoals boven of onder de controlegroep).[5]
- Als u niet zeker weet of uw gegevens zich boven of onder de controlegroep bevinden, gebruikt u een tweezijdige toets. Hiermee kunt u de significantie in beide richtingen testen.
- Als u weet in welke richting u verwacht dat uw gegevens zullen evolueren, gebruikt u een eenzijdige toets. In het gegeven voorbeeld verwacht je dat de cijfers van de student verbeteren; daarom gebruik je een eenzijdige toets.
-
 4 Bepaal de steekproefomvang met een vermogensanalyse. De kracht van een test is de waarschijnlijkheid van het waarnemen van het verwachte resultaat, gegeven een specifieke steekproefomvang.[6] De gemeenschappelijke drempel voor vermogen (of β) is 80%. Een vermogensanalyse kan een beetje lastig zijn zonder enige voorlopige gegevens, omdat u enige informatie nodig heeft over uw verwachte gemiddelden tussen elke groep en hun standaardafwijkingen. Gebruik online een rekenmachine voor vermogensanalyse om de optimale steekproefgrootte voor uw gegevens te bepalen.[7]
4 Bepaal de steekproefomvang met een vermogensanalyse. De kracht van een test is de waarschijnlijkheid van het waarnemen van het verwachte resultaat, gegeven een specifieke steekproefomvang.[6] De gemeenschappelijke drempel voor vermogen (of β) is 80%. Een vermogensanalyse kan een beetje lastig zijn zonder enige voorlopige gegevens, omdat u enige informatie nodig heeft over uw verwachte gemiddelden tussen elke groep en hun standaardafwijkingen. Gebruik online een rekenmachine voor vermogensanalyse om de optimale steekproefgrootte voor uw gegevens te bepalen.[7] - Onderzoekers doen meestal een kleine pilotstudie om hun power-analyse te informeren en de steekproefomvang te bepalen die nodig is voor een grotere, uitgebreide studie.
- Als u niet beschikt over de middelen om een complexe pilotstudie te doen, maak dan enkele schattingen over mogelijke middelen op basis van het lezen van de literatuur en studies die andere personen mogelijk hebben uitgevoerd. Dit geeft je een goede plek om te starten voor de steekproefomvang.
Tweede deel van de drie:
Berekening van de standaarddeviatie
-
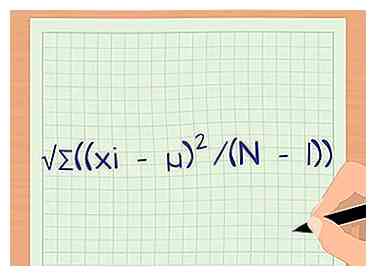 1 Definieer de formule voor standaarddeviatie. De standaarddeviatie is een maatstaf voor de spreiding van uw gegevens. Het geeft u informatie over hoe vergelijkbaar elk gegevenspunt in uw steekproef is, wat u helpt te bepalen of de gegevens significant zijn. Op het eerste gezicht lijkt de vergelijking misschien wat ingewikkeld, maar met deze stappen doorloopt u het berekeningsproces. De formule is s = √Σ ((xik - µ)2/ (N - 1)).
1 Definieer de formule voor standaarddeviatie. De standaarddeviatie is een maatstaf voor de spreiding van uw gegevens. Het geeft u informatie over hoe vergelijkbaar elk gegevenspunt in uw steekproef is, wat u helpt te bepalen of de gegevens significant zijn. Op het eerste gezicht lijkt de vergelijking misschien wat ingewikkeld, maar met deze stappen doorloopt u het berekeningsproces. De formule is s = √Σ ((xik - µ)2/ (N - 1)). - s is de standaarddeviatie.
- Σ geeft aan dat u alle verzamelde monsterwaarden wilt optellen.
- Xik vertegenwoordigt elke individuele waarde van uw gegevens.
- μ is het gemiddelde (of gemiddelde) van uw gegevens voor elke groep.
- N is het totale aantal monsters.
-
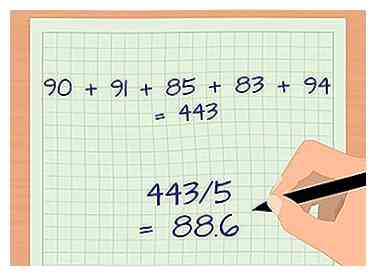 2 Gemiddeld de steekproeven in elke groep. Om de standaardafwijking te berekenen, moet u eerst het gemiddelde van de steekproeven in de afzonderlijke groepen nemen. Het gemiddelde wordt aangeduid met de Griekse letter mu of μ. Om dit te doen, voegt u eenvoudig elk monster bij elkaar en deelt u vervolgens het totale aantal monsters.[8]
2 Gemiddeld de steekproeven in elke groep. Om de standaardafwijking te berekenen, moet u eerst het gemiddelde van de steekproeven in de afzonderlijke groepen nemen. Het gemiddelde wordt aangeduid met de Griekse letter mu of μ. Om dit te doen, voegt u eenvoudig elk monster bij elkaar en deelt u vervolgens het totale aantal monsters.[8] - Als u bijvoorbeeld de gemiddelde beoordeling wilt vinden van de groep die het materiaal vóór de les heeft gelezen, laten we enkele gegevens bekijken. Voor de eenvoud gebruiken we een dataset van 5 punten: 90, 91, 85, 83 en 94.
- Voeg alle monsters samen toe: 90 + 91 + 85 + 83 + 94 = 443.
- Deel de som door het steekproefnummer, N = 5: 443/5 = 88.6.
- Het gemiddelde cijfer voor deze groep is 88.6.
-
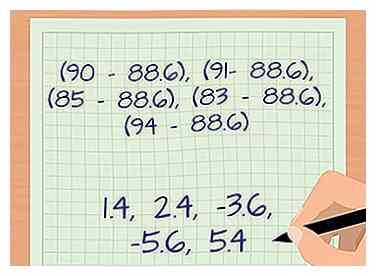 3 Trek elk monster van het gemiddelde af. Het volgende deel van de berekening betreft de (xik - μ) deel van de vergelijking. Je trekt elk monster af van het zojuist berekende gemiddelde. Voor ons voorbeeld krijg je vijf aftrekkingen.
3 Trek elk monster van het gemiddelde af. Het volgende deel van de berekening betreft de (xik - μ) deel van de vergelijking. Je trekt elk monster af van het zojuist berekende gemiddelde. Voor ons voorbeeld krijg je vijf aftrekkingen. - (90 - 88,6), (91 - 88,6), (85 - 88,6), (83 - 88,6) en (94 - 88,6).
- De berekende getallen zijn nu 1,4, 2,4, -3,6, -5,6 en 5,4.
-
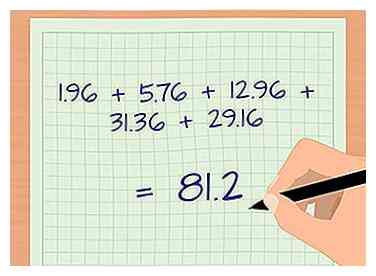 4 Zet elk van deze nummers vierkant en tel ze bij elkaar. Elk van de nieuwe nummers die u zojuist hebt berekend, krijgt nu een vierkant. Deze stap zorgt ook voor eventuele negatieve signalen. Als u na deze stap of aan het einde van uw berekening een negatief teken heeft, bent u deze stap mogelijk vergeten.
4 Zet elk van deze nummers vierkant en tel ze bij elkaar. Elk van de nieuwe nummers die u zojuist hebt berekend, krijgt nu een vierkant. Deze stap zorgt ook voor eventuele negatieve signalen. Als u na deze stap of aan het einde van uw berekening een negatief teken heeft, bent u deze stap mogelijk vergeten. - In ons voorbeeld werken we nu met 1.96, 5.76, 12.96, 31.36 en 29.16.
- Het optellen van deze vierkanten samen levert op: 1,96 + 5,76 + 12,96 + 31,36 + 29,16 = 81,2.
-
 5 Deel door het totale aantal monsters minus 1. De formule wordt gedeeld door N - 1 omdat het corrigeert voor het feit dat u geen volledige populatie hebt geteld; je neemt een steekproef van de populatie van alle studenten om een schatting te maken.[9]
5 Deel door het totale aantal monsters minus 1. De formule wordt gedeeld door N - 1 omdat het corrigeert voor het feit dat u geen volledige populatie hebt geteld; je neemt een steekproef van de populatie van alle studenten om een schatting te maken.[9] - Trek af: N - 1 = 5 - 1 = 4
- Verdelen: 81.2 / 4 = 20.3
-
 6 Neem de vierkantswortel. Heb je eenmaal gedeeld door het voorbeeldnummer min één, neem dan de vierkantswortel van dit laatste getal. Dit is de laatste stap in het berekenen van de standaardafwijking. Er zijn statistische programma's die deze berekening voor u uitvoeren na het invoeren van de onbewerkte gegevens.
6 Neem de vierkantswortel. Heb je eenmaal gedeeld door het voorbeeldnummer min één, neem dan de vierkantswortel van dit laatste getal. Dit is de laatste stap in het berekenen van de standaardafwijking. Er zijn statistische programma's die deze berekening voor u uitvoeren na het invoeren van de onbewerkte gegevens. - Voor ons voorbeeld is de standaardafwijking van de eindcijfers van studenten die vóór de les lezen: s = √20.3 = 4.51.
Derde deel van de drie:
Bepalend belang
-
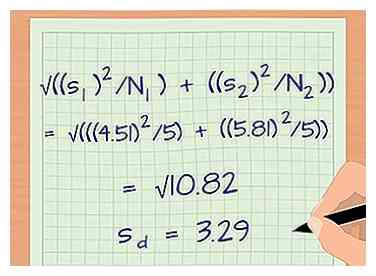 1 Bereken de variantie tussen uw 2 voorbeeldgroepen. Tot nu toe behandelde het voorbeeld slechts 1 van de voorbeeldgroepen. Als u 2 groepen probeert te vergelijken, zult u uiteraard gegevens van beide hebben. Bereken de standaarddeviatie van de tweede groep monsters en gebruik die om de variantie tussen de 2 experimentele groepen te berekenen. De formule voor variantie is sd = √ ((s1/ N1) + (s2/ N2)).[10]
1 Bereken de variantie tussen uw 2 voorbeeldgroepen. Tot nu toe behandelde het voorbeeld slechts 1 van de voorbeeldgroepen. Als u 2 groepen probeert te vergelijken, zult u uiteraard gegevens van beide hebben. Bereken de standaarddeviatie van de tweede groep monsters en gebruik die om de variantie tussen de 2 experimentele groepen te berekenen. De formule voor variantie is sd = √ ((s1/ N1) + (s2/ N2)).[10] - sd is de variantie tussen jouw groepen.
- s1 is de standaarddeviatie van groep 1 en N1 is de steekproefomvang van groep 1.
- s2 is de standaarddeviatie van groep 2 en N2 is de steekproefomvang van groep 2.
- Laten we voor ons voorbeeld zeggen dat de gegevens uit groep 2 (studenten die niet voor de les hebben gelezen) een steekproefomvang van 5 en een standaardafwijking van 5,81 hadden. De variantie is:
- sd = √ ((s1)2/ N1) + ((s2)2/ N2))
- sd = √(((4.51)2/5) + ((5.81)2/5)) = √((20.34/5) + (33.76/5)) = √(4.07 + 6.75) = √10.82 = 3.29.
-
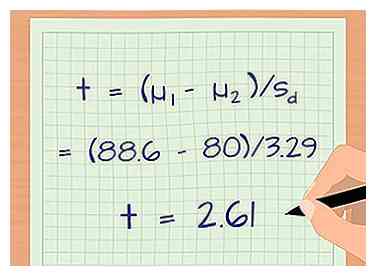 2 Bereken de t-score van uw gegevens. Met een t-score kunt u uw gegevens converteren naar een formulier waarmee u het met andere gegevens kunt vergelijken. Met T-scores kunt u een t-toets uitvoeren waarmee u de kans kunt berekenen dat twee groepen significant van elkaar verschillen. De formule voor een t-score is: t = (μ1 - µ2) / Sd.[11]
2 Bereken de t-score van uw gegevens. Met een t-score kunt u uw gegevens converteren naar een formulier waarmee u het met andere gegevens kunt vergelijken. Met T-scores kunt u een t-toets uitvoeren waarmee u de kans kunt berekenen dat twee groepen significant van elkaar verschillen. De formule voor een t-score is: t = (μ1 - µ2) / Sd.[11] - µ1 is het gemiddelde van de eerste groep.
- µ2 is het gemiddelde van de tweede groep.
- sd is de variantie tussen uw voorbeelden.
- Gebruik het grotere gemiddelde als μ1 dus je hebt geen negatieve t-waarde.
- Laten we voor ons voorbeeld zeggen dat het steekproefgemiddelde voor groep 2 (degenen die niet hebben gelezen) 80 was. De t-score is: t = (μ1 - µ2) / Sd = (88.6 - 80)/3.29 = 2.61.
-
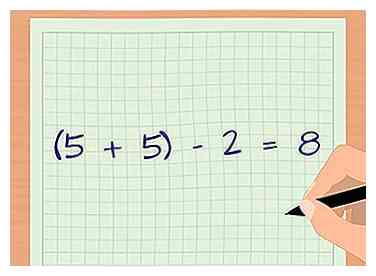 3 Bepaal de vrijheidsgraden van uw steekproef. Bij gebruik van de t-score wordt het aantal vrijheidsgraden bepaald met behulp van de steekproefomvang. Tel het aantal monsters uit elke groep bij elkaar op en trek er twee af. Voor ons voorbeeld zijn de vrijheidsgraden (d.f.) 8, omdat er vijf monsters in de eerste groep zijn en vijf monsters in de tweede groep ((5 + 5) - 2 = 8).[12]
3 Bepaal de vrijheidsgraden van uw steekproef. Bij gebruik van de t-score wordt het aantal vrijheidsgraden bepaald met behulp van de steekproefomvang. Tel het aantal monsters uit elke groep bij elkaar op en trek er twee af. Voor ons voorbeeld zijn de vrijheidsgraden (d.f.) 8, omdat er vijf monsters in de eerste groep zijn en vijf monsters in de tweede groep ((5 + 5) - 2 = 8).[12] -
 4 Gebruik een t-tabel om de significantie te evalueren. Een tabel met t-scores[13] en vrijheidsgraden zijn te vinden in een standaard statistiekenboek of online. Kijk naar de rij met de vrijheidsgraden voor uw gegevens en zoek de p-waarde die overeenkomt met uw t-score.
4 Gebruik een t-tabel om de significantie te evalueren. Een tabel met t-scores[13] en vrijheidsgraden zijn te vinden in een standaard statistiekenboek of online. Kijk naar de rij met de vrijheidsgraden voor uw gegevens en zoek de p-waarde die overeenkomt met uw t-score. - Met 8 d.f. en een t-score van 2,61, de p-waarde voor een eenzijdige toets valt tussen 0,01 en 0,025. Omdat we ons significantieniveau lager dan of gelijk aan 0,05 stellen, zijn onze gegevens statistisch significant. Met deze gegevens verwerpen we de nulhypothese en accepteren we de alternatieve hypothese:[14] studenten die het materiaal vóór de les lezen krijgen betere eindcijfers.
-
 5 Overweeg een vervolgstudie. Veel onderzoekers doen een kleine pilotstudie met enkele metingen om hen te helpen begrijpen hoe ze een grotere studie kunnen ontwerpen. Een andere studie doen, met meer metingen, zal helpen om je zelfvertrouwen over je conclusie te vergroten.
5 Overweeg een vervolgstudie. Veel onderzoekers doen een kleine pilotstudie met enkele metingen om hen te helpen begrijpen hoe ze een grotere studie kunnen ontwerpen. Een andere studie doen, met meer metingen, zal helpen om je zelfvertrouwen over je conclusie te vergroten. - Een vervolgstudie kan u helpen te bepalen of een van uw conclusies type I-fout bevat (een verschil waarnemen als er geen sprake is van een onjuiste afwijzing van de nulhypothese) of type II-fout (het niet waarnemen van een verschil als er sprake is van één, of valse acceptatie van de nulhypothese).[15]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Definieer uw hypotheses. De eerste stap bij het beoordelen van statistische significantie is het definiëren van de vraag die u wilt beantwoorden en het aangeven van uw hypothese. De hypothese is een uitspraak over uw experimentele gegevens en de verschillen die zich in de populatie kunnen voordoen. Voor elk experiment is er zowel een nul als een alternatieve hypothese.[2] Over het algemeen zul je twee groepen vergelijken om te zien of ze hetzelfde of verschillend zijn.
1 Definieer uw hypotheses. De eerste stap bij het beoordelen van statistische significantie is het definiëren van de vraag die u wilt beantwoorden en het aangeven van uw hypothese. De hypothese is een uitspraak over uw experimentele gegevens en de verschillen die zich in de populatie kunnen voordoen. Voor elk experiment is er zowel een nul als een alternatieve hypothese.[2] Over het algemeen zul je twee groepen vergelijken om te zien of ze hetzelfde of verschillend zijn.  2 Stel het significantieniveau in om te bepalen hoe ongewoon uw gegevens moeten zijn voordat deze als significant kan worden beschouwd. Het significantieniveau (ook wel alfa genoemd) is de drempel die u instelt om de significantie te bepalen. Als uw p-waarde kleiner is dan of gelijk is aan het ingestelde significantieniveau, worden de gegevens als statistisch significant beschouwd.[3]
2 Stel het significantieniveau in om te bepalen hoe ongewoon uw gegevens moeten zijn voordat deze als significant kan worden beschouwd. Het significantieniveau (ook wel alfa genoemd) is de drempel die u instelt om de significantie te bepalen. Als uw p-waarde kleiner is dan of gelijk is aan het ingestelde significantieniveau, worden de gegevens als statistisch significant beschouwd.[3]  3 Besluit om een eenzijdige of tweezijdige toets te gebruiken. Een van de aannamen die een t-toets maakt, is dat uw gegevens normaal worden verspreid. Een normale gegevensverdeling vormt een belcurve waarbij het grootste deel van de monsters in het midden valt.[4] De t-toets is een wiskundige test om te zien of uw gegevens buiten de normale verdeling vallen, hetzij boven of onder, in de "uiteinden" van de curve.
3 Besluit om een eenzijdige of tweezijdige toets te gebruiken. Een van de aannamen die een t-toets maakt, is dat uw gegevens normaal worden verspreid. Een normale gegevensverdeling vormt een belcurve waarbij het grootste deel van de monsters in het midden valt.[4] De t-toets is een wiskundige test om te zien of uw gegevens buiten de normale verdeling vallen, hetzij boven of onder, in de "uiteinden" van de curve.  4 Bepaal de steekproefomvang met een vermogensanalyse. De kracht van een test is de waarschijnlijkheid van het waarnemen van het verwachte resultaat, gegeven een specifieke steekproefomvang.[6] De gemeenschappelijke drempel voor vermogen (of β) is 80%. Een vermogensanalyse kan een beetje lastig zijn zonder enige voorlopige gegevens, omdat u enige informatie nodig heeft over uw verwachte gemiddelden tussen elke groep en hun standaardafwijkingen. Gebruik online een rekenmachine voor vermogensanalyse om de optimale steekproefgrootte voor uw gegevens te bepalen.[7]
4 Bepaal de steekproefomvang met een vermogensanalyse. De kracht van een test is de waarschijnlijkheid van het waarnemen van het verwachte resultaat, gegeven een specifieke steekproefomvang.[6] De gemeenschappelijke drempel voor vermogen (of β) is 80%. Een vermogensanalyse kan een beetje lastig zijn zonder enige voorlopige gegevens, omdat u enige informatie nodig heeft over uw verwachte gemiddelden tussen elke groep en hun standaardafwijkingen. Gebruik online een rekenmachine voor vermogensanalyse om de optimale steekproefgrootte voor uw gegevens te bepalen.[7] 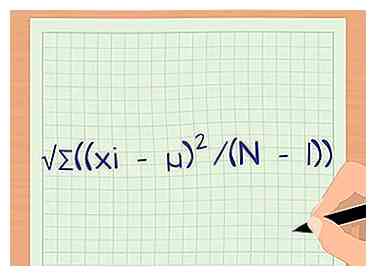 1 Definieer de formule voor standaarddeviatie. De standaarddeviatie is een maatstaf voor de spreiding van uw gegevens. Het geeft u informatie over hoe vergelijkbaar elk gegevenspunt in uw steekproef is, wat u helpt te bepalen of de gegevens significant zijn. Op het eerste gezicht lijkt de vergelijking misschien wat ingewikkeld, maar met deze stappen doorloopt u het berekeningsproces. De formule is s = √Σ ((xik - µ)2/ (N - 1)).
1 Definieer de formule voor standaarddeviatie. De standaarddeviatie is een maatstaf voor de spreiding van uw gegevens. Het geeft u informatie over hoe vergelijkbaar elk gegevenspunt in uw steekproef is, wat u helpt te bepalen of de gegevens significant zijn. Op het eerste gezicht lijkt de vergelijking misschien wat ingewikkeld, maar met deze stappen doorloopt u het berekeningsproces. De formule is s = √Σ ((xik - µ)2/ (N - 1)). 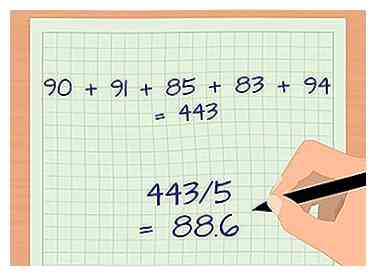 2 Gemiddeld de steekproeven in elke groep. Om de standaardafwijking te berekenen, moet u eerst het gemiddelde van de steekproeven in de afzonderlijke groepen nemen. Het gemiddelde wordt aangeduid met de Griekse letter mu of μ. Om dit te doen, voegt u eenvoudig elk monster bij elkaar en deelt u vervolgens het totale aantal monsters.[8]
2 Gemiddeld de steekproeven in elke groep. Om de standaardafwijking te berekenen, moet u eerst het gemiddelde van de steekproeven in de afzonderlijke groepen nemen. Het gemiddelde wordt aangeduid met de Griekse letter mu of μ. Om dit te doen, voegt u eenvoudig elk monster bij elkaar en deelt u vervolgens het totale aantal monsters.[8] 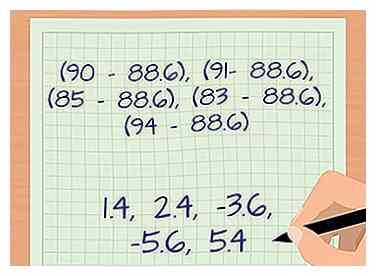 3 Trek elk monster van het gemiddelde af. Het volgende deel van de berekening betreft de (xik - μ) deel van de vergelijking. Je trekt elk monster af van het zojuist berekende gemiddelde. Voor ons voorbeeld krijg je vijf aftrekkingen.
3 Trek elk monster van het gemiddelde af. Het volgende deel van de berekening betreft de (xik - μ) deel van de vergelijking. Je trekt elk monster af van het zojuist berekende gemiddelde. Voor ons voorbeeld krijg je vijf aftrekkingen. 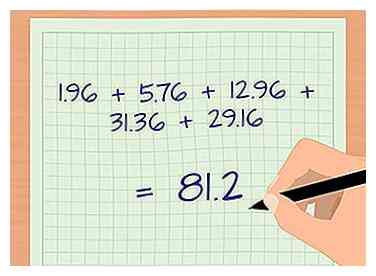 4 Zet elk van deze nummers vierkant en tel ze bij elkaar. Elk van de nieuwe nummers die u zojuist hebt berekend, krijgt nu een vierkant. Deze stap zorgt ook voor eventuele negatieve signalen. Als u na deze stap of aan het einde van uw berekening een negatief teken heeft, bent u deze stap mogelijk vergeten.
4 Zet elk van deze nummers vierkant en tel ze bij elkaar. Elk van de nieuwe nummers die u zojuist hebt berekend, krijgt nu een vierkant. Deze stap zorgt ook voor eventuele negatieve signalen. Als u na deze stap of aan het einde van uw berekening een negatief teken heeft, bent u deze stap mogelijk vergeten.  5 Deel door het totale aantal monsters minus 1. De formule wordt gedeeld door N - 1 omdat het corrigeert voor het feit dat u geen volledige populatie hebt geteld; je neemt een steekproef van de populatie van alle studenten om een schatting te maken.[9]
5 Deel door het totale aantal monsters minus 1. De formule wordt gedeeld door N - 1 omdat het corrigeert voor het feit dat u geen volledige populatie hebt geteld; je neemt een steekproef van de populatie van alle studenten om een schatting te maken.[9]  6 Neem de vierkantswortel. Heb je eenmaal gedeeld door het voorbeeldnummer min één, neem dan de vierkantswortel van dit laatste getal. Dit is de laatste stap in het berekenen van de standaardafwijking. Er zijn statistische programma's die deze berekening voor u uitvoeren na het invoeren van de onbewerkte gegevens.
6 Neem de vierkantswortel. Heb je eenmaal gedeeld door het voorbeeldnummer min één, neem dan de vierkantswortel van dit laatste getal. Dit is de laatste stap in het berekenen van de standaardafwijking. Er zijn statistische programma's die deze berekening voor u uitvoeren na het invoeren van de onbewerkte gegevens. 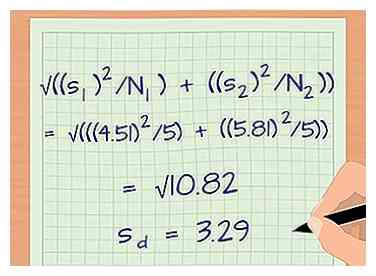 1 Bereken de variantie tussen uw 2 voorbeeldgroepen. Tot nu toe behandelde het voorbeeld slechts 1 van de voorbeeldgroepen. Als u 2 groepen probeert te vergelijken, zult u uiteraard gegevens van beide hebben. Bereken de standaarddeviatie van de tweede groep monsters en gebruik die om de variantie tussen de 2 experimentele groepen te berekenen. De formule voor variantie is sd = √ ((s1/ N1) + (s2/ N2)).[10]
1 Bereken de variantie tussen uw 2 voorbeeldgroepen. Tot nu toe behandelde het voorbeeld slechts 1 van de voorbeeldgroepen. Als u 2 groepen probeert te vergelijken, zult u uiteraard gegevens van beide hebben. Bereken de standaarddeviatie van de tweede groep monsters en gebruik die om de variantie tussen de 2 experimentele groepen te berekenen. De formule voor variantie is sd = √ ((s1/ N1) + (s2/ N2)).[10] 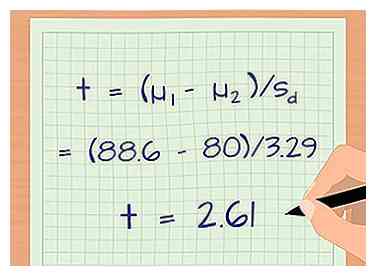 2 Bereken de t-score van uw gegevens. Met een t-score kunt u uw gegevens converteren naar een formulier waarmee u het met andere gegevens kunt vergelijken. Met T-scores kunt u een t-toets uitvoeren waarmee u de kans kunt berekenen dat twee groepen significant van elkaar verschillen. De formule voor een t-score is: t = (μ1 - µ2) / Sd.[11]
2 Bereken de t-score van uw gegevens. Met een t-score kunt u uw gegevens converteren naar een formulier waarmee u het met andere gegevens kunt vergelijken. Met T-scores kunt u een t-toets uitvoeren waarmee u de kans kunt berekenen dat twee groepen significant van elkaar verschillen. De formule voor een t-score is: t = (μ1 - µ2) / Sd.[11] 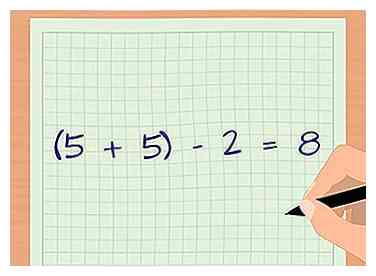 3 Bepaal de vrijheidsgraden van uw steekproef. Bij gebruik van de t-score wordt het aantal vrijheidsgraden bepaald met behulp van de steekproefomvang. Tel het aantal monsters uit elke groep bij elkaar op en trek er twee af. Voor ons voorbeeld zijn de vrijheidsgraden (d.f.) 8, omdat er vijf monsters in de eerste groep zijn en vijf monsters in de tweede groep ((5 + 5) - 2 = 8).[12]
3 Bepaal de vrijheidsgraden van uw steekproef. Bij gebruik van de t-score wordt het aantal vrijheidsgraden bepaald met behulp van de steekproefomvang. Tel het aantal monsters uit elke groep bij elkaar op en trek er twee af. Voor ons voorbeeld zijn de vrijheidsgraden (d.f.) 8, omdat er vijf monsters in de eerste groep zijn en vijf monsters in de tweede groep ((5 + 5) - 2 = 8).[12]  4 Gebruik een t-tabel om de significantie te evalueren. Een tabel met t-scores[13] en vrijheidsgraden zijn te vinden in een standaard statistiekenboek of online. Kijk naar de rij met de vrijheidsgraden voor uw gegevens en zoek de p-waarde die overeenkomt met uw t-score.
4 Gebruik een t-tabel om de significantie te evalueren. Een tabel met t-scores[13] en vrijheidsgraden zijn te vinden in een standaard statistiekenboek of online. Kijk naar de rij met de vrijheidsgraden voor uw gegevens en zoek de p-waarde die overeenkomt met uw t-score.  5 Overweeg een vervolgstudie. Veel onderzoekers doen een kleine pilotstudie met enkele metingen om hen te helpen begrijpen hoe ze een grotere studie kunnen ontwerpen. Een andere studie doen, met meer metingen, zal helpen om je zelfvertrouwen over je conclusie te vergroten.
5 Overweeg een vervolgstudie. Veel onderzoekers doen een kleine pilotstudie met enkele metingen om hen te helpen begrijpen hoe ze een grotere studie kunnen ontwerpen. Een andere studie doen, met meer metingen, zal helpen om je zelfvertrouwen over je conclusie te vergroten.