Mastermind is een moeilijk puzzelspel, waarin een speler de code probeert te raden die zijn tegenstander bedacht. Oorspronkelijk was een bordspel, hoewel met wortels in eerdere pen-en-papier-games, Mastermind nu op grote schaal online beschikbaar en ook voor mobiele apparaten.

Je kunt Mastermind ook spelen met papier en pen als je het bordspel of de versie van het videospelletje niet hebt.

Deel een van de drie:
Mastermind spelen

  1. 1 Laat de codemaker een code selecteren. Mastermind-bordspellen hebben een rij gaatjes die aan één kant van het bord zijn uitgespaard en die onder een scharnierend schild aan het zicht worden onttrokken. De persoon die de codemaker speelt neemt stiekem een ​​paar gekleurde pinnen en plaatst ze in die rij gaten, in willekeurige volgorde. Dit is de code die de codebreker probeert te raden.
    • Als u een versie van een videogame speelt, zal de computer dit meestal doen in plaats van een speler.
    • De codemaker moet een peg in elk gat plaatsen. Hij heeft de mogelijkheid om meerdere pinnen van dezelfde kleur te gebruiken. Hij zou bijvoorbeeld kunnen neerleggen Groen Geel Geel Blauw.
  2. 2 Laat de codebreker haar eerste gok plaatsen. De andere speler, of de enige speler in versies van videogames, probeert te raden wat de verborgen code is. Zittend aan het andere uiteinde van het bord pakt ze de grote gekleurde pinnen op en plaatst ze in de dichtstbijzijnde rij grote gaten.
    • Ze zou bijvoorbeeld kunnen neerleggen Blauw Oranje Groen Purper. (Je Mastermind-game heeft mogelijk meer gaten of verschillende gekleurde pegs.)
  3. 3 Vraag de codemaker om feedback te geven. Naast elke "gokrij" is een vierkantje met voldoende gaten voor vier kleine pinnen. Deze pegs zijn alleen verkrijgbaar in twee kleuren: wit en rood (of in sommige versies wit en zwart). De codemaker gebruikt dit om aanwijzingen te geven over hoe goed de gok was. De codemaker moet eerlijk zijn en altijd pinnen plaatsen met behulp van deze instructies:
    • Elke witte pin betekent dat een van de geraden pinnen correct is, maar in het verkeerde gat zit.
    • Elke rode (of zwarte) pin betekent dat een van de geraden pinnen correct is en in het juiste gat zit.
    • De volgorde van de witte en zwarte pinnen doet er niet toe.
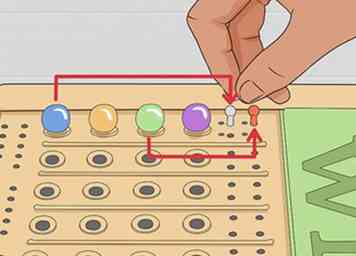  4. 4 Leer door voorbeelden. In ons voorbeeld hierboven koos de codemaker in het geheim Geel Geel Groen Blauw. De codebreker geraden Blauw Oranje Groen Paars. De codemaker bekijkt deze schatting om erachter te komen welke hintpegs moeten worden geplaatst:
    • Peg # 1 is Blauw. Er staat een blauw in de code, maar deze bevindt zich niet in positie # 1. Dit levert een witte hintpeg op.
    • Peg # 2 is Oranje. Er zit geen oranje in de code, dus geen hintpeg wordt neergezet.
    • Peg # 3 is Groen. Er staat een groen in de code en deze staat in positie # 3. Dit levert een rode (of zwarte) hintpeg op.
    • Peg # 4 is Purper. Er staat geen paarse code in de code, dus er wordt geen hintpeg neergezet.
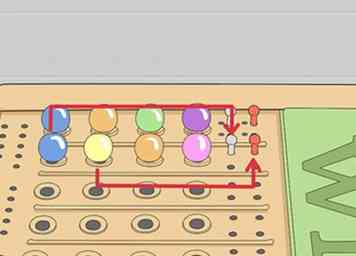  5. 5 Herhaal met de volgende rij. De codebreker heeft nu een beetje informatie. In ons voorbeeld kreeg ze een witte hint, een rode hint en twee lege gaten. Dat betekent dat van de vier pinnen die ze neerlegt, een van hen hoort, maar verplaatst moet worden naar een ander gat, een van hen is al op de juiste plaats en twee van hen horen niet thuis in de code. Ze denkt een tijdje na en maakt een tweede gok in de volgende rij:
    • De codebreker raadt Blauw Geeloranje roze deze keer.
    • De codemaker controleert deze schatting: Blauw behoort maar is op de verkeerde plaats; Geel hoort en is op de juiste plaats; Oranje hoort niet; Roze hoort niet thuis.
    • De codemaker zet een witte hintpeg en een rode hintpeg neer.
  6. 6 Ga door totdat de code is geraden of er geen schattingen meer over zijn. De codebreker blijft gissen en gebruikt informatie uit alle eerdere hints die ze heeft verdiend. Als ze de volledige code in de juiste volgorde weet te raden, wint ze de game. Als ze niet raad weet en elke rij met pinnen vult, wint de codemaker in plaats daarvan.
  7. 7 Wissel van plaats en speel opnieuw. Als je een spel voor twee personen speelt, draai je het bord zodat een andere persoon de code uitvindt en de andere persoon raadt. Op deze manier krijgt iedereen de kans om het hoofdgedeelte van het spel te spelen: de code raden.

Tweede deel van de drie:
Een methodische aanpak gebruiken

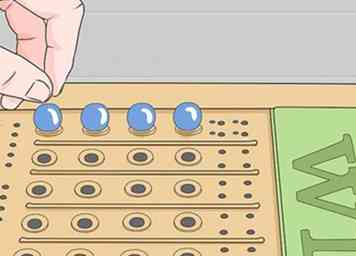  1. 1 Begin met het raden van four of a kind. Een nieuwe Mastermind-speler leert snel dat zelfs een gok die meerdere hints oplevert niet altijd tot een snelle overwinning leidt, omdat er zoveel manieren zijn om de hints te interpreteren. Beginnend met four of a kind (zoals Blauw Blauw Blauw Blauw) geeft u goede informatie om meteen mee te werken.[1]
    • Dit is niet de enige strategie om in Mastermind te gebruiken, maar het is een makkelijke manier om het op te pakken. Het zal niet erg goed werken als je versie meer dan zes kleuren heeft om uit te kiezen.
  2. 2 Gebruik 2-2 patronen om de kleuren te detecteren. De volgende paar zetten zullen twee paar kleuren zijn, altijd beginnend met twee voorbeelden van de kleur die je eerder geraden had. Volgend voorbeeld Blauw Blauw Blauw Blauw, maak schattingen die beginnen met Blauw Blauw en eindig met een andere kleur, totdat je alle beschikbare kleuren kent. Hier is een voorbeeld:
    • Blauw Blauw Blauw Blauw - Geen hintpinnen. Dat is prima, we zullen Blue toch blijven gebruiken.
    • Blauw Blauw Groen Groen - een witte pen. We houden er rekening mee dat de code één groen heeft en dat deze zich in de linker helft moet bevinden.
    • Blauw Blauw Roze roze - een zwarte peg. We weten nu dat er een roze in de code staat, rechts.
    • Blauw Blauw Geel Geel - een witte pen en een zwarte pen. Er moeten minstens twee gele tekens in de code staan, één aan de linkerkant en één aan de rechterkant.
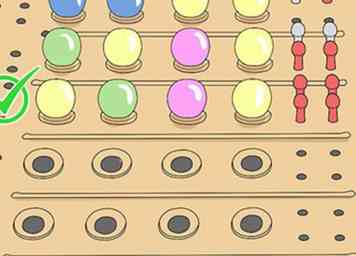  3. 3 Gebruik logica om de bekende pegs opnieuw te ordenen. Als je in totaal vier hintpegs hebt verdiend, weet je precies welke kleuren zijn betrokken, maar niet in welke volgorde. In ons voorbeeld moet de code groen, roze, geel en geel bevatten. Het systeem om het bord in twee paren te verdelen, heeft ons ook informatie gegeven over de volgorde waarin ze moeten worden geplaatst, dus we moeten dit in één of drie keer kunnen raden:
    • We weten dat Groen Geel Roze Geel heb een linkerhelft en rechterhelft die de juiste pegs bevatten, maar het blijkt dat we twee witte pinnen en twee zwarte pegs in onze resultaten krijgen. Dit betekent een van de helften (ofwel # 1 en # 2 moeten van plaats wisselen, of anders # 3 en # 4 doen).
    • We proberen Geel Groen Roze Geel en krijg vier zwarte pegs - de code is opgelost.

Derde deel van de drie:
Voorbeeld van een krachtige methodische aanpak (2)

  1. 1 Elimineer tegelijkertijd twee kleuren (met 4 onbekende pinnen). Bijvoorbeeld rood en blauw:
    • Rood Rood Blauw Blauw
    • Resultaat 1: geen pegs: rood en blauw staan ​​niet in de code
    • Resultaat 2: een witte of zwarte peg (laat een witte peg veronderstellen). Rood of blauw is één keer in de code. Blauw Blauw Blauw Blauw geeft je een peg als deze blauw is, of geen pinnen als deze rood is (laten we aannemen dat er geen pinnen zijn). In het voorbeeld weten we nu dat er een rode pin is en dat deze op de 3e of 4e plek staat (omdat we een witte pin kregen op Rood Rood Blauw Blauw). Het vinden ervan zal worden besproken in de volgende strategie (in één stap: Rood Groen Groen Groen ).
    • Resultaat 3: meer pegs (laat twee witte pegs veronderstellen). Net als resultaat 2, kunnen we het proberen Blauw Blauw Blauw Blauw om te weten hoeveel pinnen blauw waren (laat opnieuw nul veronderstellen). Nu is het alleen maar een kwestie om de pinnen te vinden. In het voorbeeld weten we al dat de 3e en 4e rode pinnen zijn, omdat er 2 rode pinnen zijn en ze niet op de eerste of tweede plek staan ​​(omdat we 2 witte pinnen hebben gekregen)
  2. 2 Zoek de locatie van een rood, als je weet dat er ten minste één rode pin is, maar weet niet in wat van de gaten het zou moeten zijn. U kunt een pincode vinden door elk van de locaties te proberen. Als alternatieve kleur gebruiken we kleuren die we nog niet hebben getest. Op deze manier vinden we niet alleen de rode pin, maar ook aanvullende informatie over andere kleuren. Het volgende is een voorbeeld, als je weet dat er een rode pin is, maar niet weet in welke van de vier holes het is. Het geeft je ook de hoeveelheid groen, geel en roze.
    • Rood Groen Groen Groen
    • Geel Rood Geel Geel
    • Roze roze Rood Roze
    • Notitie: Als u het exacte aantal rode punten weet, hoeft u de laatste locatie niet te proberen: als er één rode pin is en deze zich niet op de eerste, tweede of derde locatie bevindt, moet deze in de vierde staan).
    • Resultaat 1: Als er geen witte pegs zijn, hebt u ten minste één zwarte peg. Die peg geeft aan dat de rode pin op de juiste locatie staat
    • Resultaat 2: Als er een witte koppeling is, weet u dat de rode pin op een onjuiste plaats staat en dat de alternatieve kleur niet in de code voorkomt
    • Resultaat 3: Als er een tweede witte koppeling is, weet je dat de tweede kleur op de locatie moet staan ​​waar de rode pin staat.
    • Resultaat 4: Als er een of meer zwarte pegs zijn, geeft dit aan dat de tweede kleur aanwezig is. Het geeft je ook het aantal pinnen van die kleur, en je weet dat het niet op de locatie is waar rood is (omdat dat een witte peg zou geven), of, natuurlijk, op de locatie waar rood uiteindelijk wordt
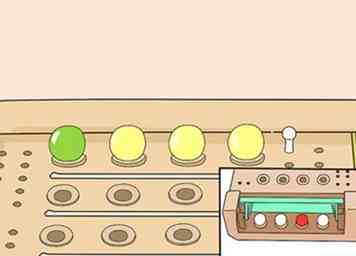  3. 3 Elimineer tegelijkertijd twee kleuren (met 3 onbekende pinnen). Zet een kleur in de plaats die je kent, en de andere kleur op de plaatsen die je niet kent. Bijvoorbeeld groen en geel, en we weten dat de eerste pin rood is:
    • Groen Geel Geel Geel
    • Resultaat 1: geen pinnen; groen en geel staan ​​niet in de code
    • Resultaat 2a: een witte peg geeft aan dat er groen in de code zit, maar we weten het bedrag niet (het kan er een zijn, maar ook twee of zelfs drie)
    • Resultaat 2b: het aantal zwarte pegs geeft de hoeveelheid geel in de code aan (zoals opgemerkt in Strategie 2: als u weet wat de exacte hoeveelheid is, kunt u een stap besparen bij het vinden van de kleur)
  4. 4 Elimineer tegelijkertijd twee kleuren (met slechts 1 of 2 onbekende pinnen). Deze strategie lijkt veel op de vorige strategie, maar nu geeft de hoeveelheid witte pinnen ons ook de hoeveelheid van die kleur, bijvoorbeeld groen en geel, en we weten dat de eerste twee pinnen rood zijn:
    • Groen Groen Geel Geel
    • Resultaat 1: geen pinnen: groen en geel staan ​​niet in de code
    • Resultaat 2a: een witte peg geeft aan dat er één groen in de code zit, terwijl 2 pinnen aangeven dat er groen in de code staat (aangezien er slechts 2 onbekenden zijn, is het onmogelijk dat er drie greens zijn)
    • Resultaat 2b: net als bij de vorige strategie, geeft het aantal zwarte pegs de hoeveelheid geel in de code aan. (zoals opgemerkt in Strategie 2: als u weet wat de precieze hoeveelheid is, kunt u een stap besparen bij het vinden van de kleur)
  5. 5 Leer van een voorbeeld. In dit voorbeeld beginnen we zoals altijd met strategie 1 ...
    • (strategie 1) Blauw Blauw Rood Rood geeft 2 witte pinnen. Dus we weten dat er rood en / of blauw aanwezig is. We willen weten welke blauw is en welke rood is, dus we controleren:
    • (strategie 1 bis) Blauw Blauw Blauw Blauw geeft een zwarte peg. Dit betekent dat we in het vorige antwoord weten dat er één blauw is (en op de verkeerde plek - dus zal het 3de of 4de zijn), en dus ook een rood (en ook op de verkeerde plek, dus 1ste of 2de)
    • (strategie 2 (vind blauw)) Groen groen Blauw Groen geeft witte en zwarte pinnen. We hebben een van de locaties van blauw getest en omdat er een witte koppeling is, weten we dat dit niet de derde peg is. Zoals we weten was het de derde of vierde pin, we weten dat de vierde pin blauw is. De zwarte peg geeft ook aan dat er een groene koppeling is, maar het is niet de derde plek (omdat het een zwarte koppeling is, geen witte koppeling).
    • (strategie 2 (vind rood)) Rood Geel Geel Geel geeft een enkele witte peg, dus terwijl we weten dat rood op de eerste of tweede plek staat, weten we nu dat het niet op de eerste plek staat. Dus het is op de tweede locatie. We weten ook dat er geen gele kleur is
    • De volgende kleur waarover we informatie hadden was groen - maar zoals we weten is het niet de derde plek, en de tweede en vierde plek zijn gevuld met blauw en rood, we weten dat het op de eerste plek staat.
    • (strategie 4) Oranje Oranje Roze Oranje Geeft een witte koppeling. Dus we weten dat de enige onbekende plek - de 3e plek - een oranje kleur heeft
    • (antwoord) Groen Rood Oranje Blauw