De tweetample t-test is een van de meest gebruikte statistische tests. Het wordt toegepast om te vergelijken of de gemiddelden van twee gegevenssets significant verschillend zijn, of dat het verschil te wijten is aan willekeurig toeval alleen. Het kan worden gebruikt om te bepalen of een nieuwe lesmethode echt heeft geholpen een groep kinderen beter te leren, of dat die groep gewoon intelligenter is. Of, zoals in het onderstaande voorbeeld, zou het kunnen worden gebruikt om te bepalen of de nieuwe snellere auto's die worden gebruikt voor het bezorgen van pizza's echt hebben geholpen om de levertijden te versnellen!
Stappen
-
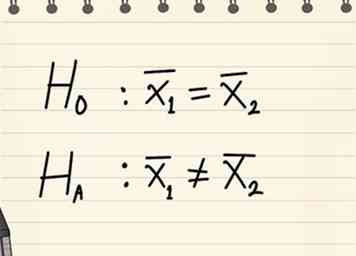 1 Bepaal een nul en alternatieve hypothese.
1 Bepaal een nul en alternatieve hypothese. - Over het algemeen zal de nulhypothese stellen dat de twee bevolkingsgroepen die worden getest geen statistisch significant verschil hebben.
- De alternatieve hypothese zal stellen dat er een aanwezig is.
-
 2 Bepaal een betrouwbaarheidsinterval.
2 Bepaal een betrouwbaarheidsinterval. - We zullen dit het alpha (α) -niveau noemen. De typische waarde is 0,05. Dit betekent dat er 95% vertrouwen is dat de conclusie van deze test geldig zal zijn.
-
 3 Wijs elke populatie toe aan een van de twee datasets.
3 Wijs elke populatie toe aan een van de twee datasets. - Deze waarden moeten duidelijk zijn bij het gebruik van de vergelijking.
-
 4 Bepaal de n1- en n2-waarden.
4 Bepaal de n1- en n2-waarden. - Deze zijn gelijk aan de twee steekproefgrootten, of het aantal gegevenspunten in elke populatie.
-
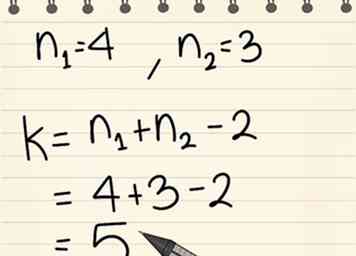 5 Bepaal de vrijheidsgraden.
5 Bepaal de vrijheidsgraden. - We zullen dit de k-waarde noemen. Op de t-distributietabel hieronder wordt deze waarde df genoemd.
- Om deze waarde te berekenen, voegt u beide n-waarden samen toe en trekt u 2 af.
-
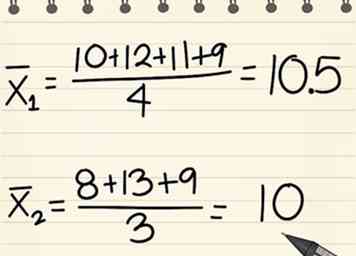 6 Bepaal de gemiddelden van de twee sample sets.
6 Bepaal de gemiddelden van de twee sample sets. - We zullen deze x̄1 en x̄2 noemen.
- Dit wordt berekend door alle gegevenspunten in elke steekproefset samen toe te voegen en vervolgens te delen door het aantal gegevenspunten in de set (de bijbehorende n-waarde).
-
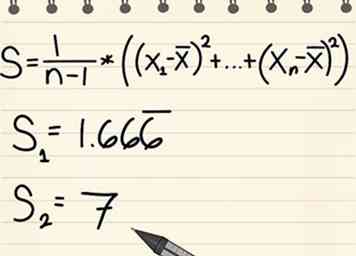 7 Bepaal de varianties van elke dataset.
7 Bepaal de varianties van elke dataset. - We noemen dit de S-waarden.
- Dit is een getal dat beschrijft hoeveel de gegevens binnen de eigen sampleset verschillen. Gebruik de volgende formule.
-
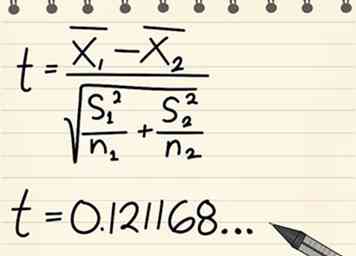 8 Bereken de t-statistiek met behulp van de volgende formule.
8 Bereken de t-statistiek met behulp van de volgende formule. -
 9 Gebruik de alpha- en k-waarden om de kritieke t-waarde op de t-distributietabel te vinden.
9 Gebruik de alpha- en k-waarden om de kritieke t-waarde op de t-distributietabel te vinden. -
 10 Vergelijk de kritische t-waarde en de berekende t-statistiek.
10 Vergelijk de kritische t-waarde en de berekende t-statistiek. - Als de berekende t-statistiek groter is dan de kritische t-waarde, concludeert de test dat er een statistisch significant verschil is tussen de twee populaties.
- Daarom verwerpt u de nulhypothese dat er geen statistisch significant verschil is tussen de twee populaties.
- In alle andere gevallen is er geen statistisch significant verschil tussen de twee populaties.
- De test faalt in het verwerpen van de nulhypothese.
- Als de berekende t-statistiek groter is dan de kritische t-waarde, concludeert de test dat er een statistisch significant verschil is tussen de twee populaties.
-
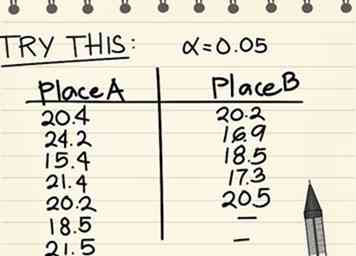 11 Gebruik het volgende voorbeeldprobleem om de hierboven gegeven vergelijkingen te oefenen.
11 Gebruik het volgende voorbeeldprobleem om de hierboven gegeven vergelijkingen te oefenen.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
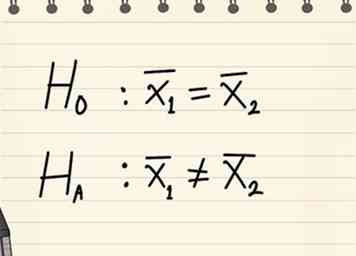 1 Bepaal een nul en alternatieve hypothese.
1 Bepaal een nul en alternatieve hypothese.  2 Bepaal een betrouwbaarheidsinterval.
2 Bepaal een betrouwbaarheidsinterval.  3 Wijs elke populatie toe aan een van de twee datasets.
3 Wijs elke populatie toe aan een van de twee datasets.  4 Bepaal de n1- en n2-waarden.
4 Bepaal de n1- en n2-waarden. 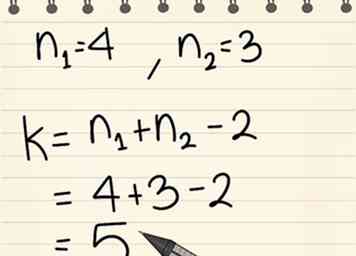 5 Bepaal de vrijheidsgraden.
5 Bepaal de vrijheidsgraden. 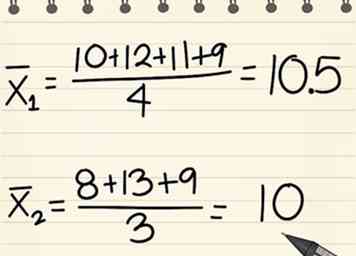 6 Bepaal de gemiddelden van de twee sample sets.
6 Bepaal de gemiddelden van de twee sample sets. 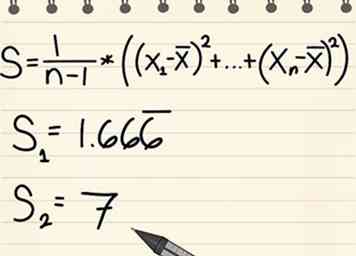 7 Bepaal de varianties van elke dataset.
7 Bepaal de varianties van elke dataset. 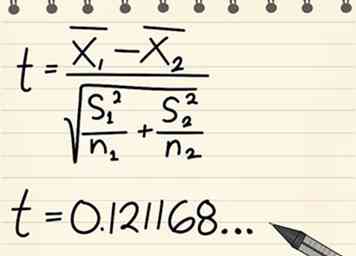 8 Bereken de t-statistiek met behulp van de volgende formule.
8 Bereken de t-statistiek met behulp van de volgende formule.  9 Gebruik de alpha- en k-waarden om de kritieke t-waarde op de t-distributietabel te vinden.
9 Gebruik de alpha- en k-waarden om de kritieke t-waarde op de t-distributietabel te vinden.  10 Vergelijk de kritische t-waarde en de berekende t-statistiek.
10 Vergelijk de kritische t-waarde en de berekende t-statistiek.  11 Gebruik het volgende voorbeeldprobleem om de hierboven gegeven vergelijkingen te oefenen.
11 Gebruik het volgende voorbeeldprobleem om de hierboven gegeven vergelijkingen te oefenen.