Een box- en whiskerplot is een diagram dat de statistische verdeling van een set gegevens toont. Dit maakt het gemakkelijk om te zien hoe gegevens worden gedistribueerd langs een getallenlijn en het is gemakkelijk om er zelf een te maken!
Stappen
-
 1 Verzamel uw gegevens. Laten we zeggen dat we de nummers 1, 3, 2, 4 en 5 beginnen. Deze worden gebruikt voor rekenvoorbeelden.
1 Verzamel uw gegevens. Laten we zeggen dat we de nummers 1, 3, 2, 4 en 5 beginnen. Deze worden gebruikt voor rekenvoorbeelden. -
 2 Organiseer de gegevens van minst naar beste. Neem al je nummers en rangschik ze op volgorde, zodat de kleinste cijfers aan de linkerkant en de grootste nummers aan je rechterkant zijn. In ons geval is de volgorde van de nummers 1, 2, 3, 4 en 5.
2 Organiseer de gegevens van minst naar beste. Neem al je nummers en rangschik ze op volgorde, zodat de kleinste cijfers aan de linkerkant en de grootste nummers aan je rechterkant zijn. In ons geval is de volgorde van de nummers 1, 2, 3, 4 en 5. -
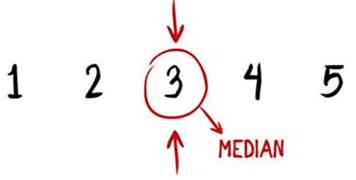 3 Zoek de mediaan van de dataset. De mediaan is het middelste cijfer in een geordende gegevensset. (Daarom hebben we alle getallen in stap 2 opgesteld.) Voor de gegevensset in ons voorbeeld is 3 het getal dat precies in het midden ligt en daarom onze mediaan is. De mediaan wordt ook wel de tweede kwartiel.
3 Zoek de mediaan van de dataset. De mediaan is het middelste cijfer in een geordende gegevensset. (Daarom hebben we alle getallen in stap 2 opgesteld.) Voor de gegevensset in ons voorbeeld is 3 het getal dat precies in het midden ligt en daarom onze mediaan is. De mediaan wordt ook wel de tweede kwartiel. - In een gegevensset met een oneven aantal getallen, heeft de mediaan aan beide zijden altijd hetzelfde aantal getallen. Voor de gegevensverzameling 1, 2, 3, 4, 5 heeft het mediaannummer, 3, 2 getallen ervoor en 2 getallen erachter. Dat is hoe we er zeker van kunnen zijn dat het onze mediaan is.
- Wat als de gegevensset waarmee u werkt een even aantal heeft? Wat als u de mediaan van 2, 4, 4, 7, 9, 10, 14, 15 zou moeten vinden? Je vindt de mediaan hier door de twee middelste cijfers te nemen en hun gemiddelde te vinden. In ons voorbeeld zou je 7 en 9 - de twee middelste getallen - optellen en ze verdelen met 2. 7 + 9 is gelijk aan 16 en 16 gedeeld door 2 gelijk aan 8. De mediaan van deze dataset zou 8 zijn.
-
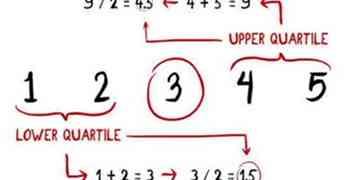 4 Zoek het eerste en derde kwartiel. We hebben het tweede kwartiel van de dataset al gevonden, onze mediaan. Nu moeten we de mediaan van de onderste helft van de dataset vinden; in ons voorbeeld zou het de mediaan zijn van de twee nummers naar de links van 3. De mediaan van 1 en 2 is (1 + 2) / 2 = 1,5. Doe hetzelfde om de mediaan van de twee nummers te vinden in de rechts van 3. (4 + 5) / 2 = 4.5.
4 Zoek het eerste en derde kwartiel. We hebben het tweede kwartiel van de dataset al gevonden, onze mediaan. Nu moeten we de mediaan van de onderste helft van de dataset vinden; in ons voorbeeld zou het de mediaan zijn van de twee nummers naar de links van 3. De mediaan van 1 en 2 is (1 + 2) / 2 = 1,5. Doe hetzelfde om de mediaan van de twee nummers te vinden in de rechts van 3. (4 + 5) / 2 = 4.5. -
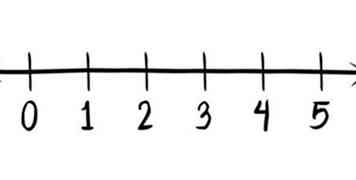 5 Teken een plotlijn. Dit moet lang genoeg zijn om al uw gegevens te bevatten, plus een beetje extra aan elke kant. Zorg ervoor dat de nummers met gelijke intervallen worden geplaatst. Als u decimalen gebruikt, zoals 4.5 en 1.5, moet u deze ook labelen.
5 Teken een plotlijn. Dit moet lang genoeg zijn om al uw gegevens te bevatten, plus een beetje extra aan elke kant. Zorg ervoor dat de nummers met gelijke intervallen worden geplaatst. Als u decimalen gebruikt, zoals 4.5 en 1.5, moet u deze ook labelen. - 6 Markeer uw eerste, tweede en derde kwartielen op de plotlijn. Neem de waarden van uw eerste, tweede en derde kwartielen en markeer die getallen op de plotlijn. Het teken moet een verticale lijn zijn bij elk kwartiel, iets boven de tekenlijn.
-
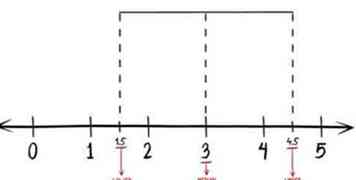 7 Maak een doos door horizontale lijnen te tekenen die de kwartielen verbinden. Verbind het bovenste of het eerste kwartiel met de bovenkant van het derde kwartiel en doorloop het tweede kwartiel. Verbind de onderkant van het eerste kwartiel met de onderkant van het derde kwartiel en zorg ervoor dat je door het tweede kwartiel gaat.
7 Maak een doos door horizontale lijnen te tekenen die de kwartielen verbinden. Verbind het bovenste of het eerste kwartiel met de bovenkant van het derde kwartiel en doorloop het tweede kwartiel. Verbind de onderkant van het eerste kwartiel met de onderkant van het derde kwartiel en zorg ervoor dat je door het tweede kwartiel gaat. -
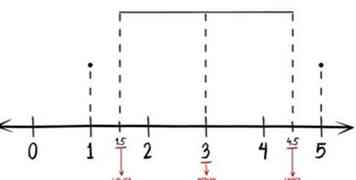 8 Markeer uw uitschieters. Zoek de kleinste en vervolgens de grootste cijfers in uw gegevensset en markeer deze op de plotlijn. Markeer deze punten met een kleine stip. In het geval van ons voorbeeld is de onderste uitbijter 1 en de bovenste uitbijter 5.
8 Markeer uw uitschieters. Zoek de kleinste en vervolgens de grootste cijfers in uw gegevensset en markeer deze op de plotlijn. Markeer deze punten met een kleine stip. In het geval van ons voorbeeld is de onderste uitbijter 1 en de bovenste uitbijter 5. -
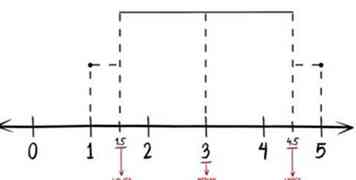 9 Verbind uw uitbijters met de doos met een horizontale lijn. De rechte lijn die de uitbijters verbindt, wordt informeel de "snorharen" van de doos en de snorharenplot genoemd.
9 Verbind uw uitbijters met de doos met een horizontale lijn. De rechte lijn die de uitbijters verbindt, wordt informeel de "snorharen" van de doos en de snorharenplot genoemd. - 10 Afgewerkt. Bekijk een kader en snorharen om de verdeling van getallen in elke gegevensset te visualiseren. U kunt bijvoorbeeld gemakkelijk zien of de getallen in de gegevensverzameling meer in het bovenste kwartiel samenkomen door te kijken naar de grootte van het bovenste vak en de grootte van de bovenste snaar. Box- en whiskerplots zijn geweldige alternatieven voor staafdiagrammen en histogrammen.[1]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Verzamel uw gegevens. Laten we zeggen dat we de nummers 1, 3, 2, 4 en 5 beginnen. Deze worden gebruikt voor rekenvoorbeelden.
1 Verzamel uw gegevens. Laten we zeggen dat we de nummers 1, 3, 2, 4 en 5 beginnen. Deze worden gebruikt voor rekenvoorbeelden.  2 Organiseer de gegevens van minst naar beste. Neem al je nummers en rangschik ze op volgorde, zodat de kleinste cijfers aan de linkerkant en de grootste nummers aan je rechterkant zijn. In ons geval is de volgorde van de nummers 1, 2, 3, 4 en 5.
2 Organiseer de gegevens van minst naar beste. Neem al je nummers en rangschik ze op volgorde, zodat de kleinste cijfers aan de linkerkant en de grootste nummers aan je rechterkant zijn. In ons geval is de volgorde van de nummers 1, 2, 3, 4 en 5.  3 Zoek de mediaan van de dataset. De mediaan is het middelste cijfer in een geordende gegevensset. (Daarom hebben we alle getallen in stap 2 opgesteld.) Voor de gegevensset in ons voorbeeld is 3 het getal dat precies in het midden ligt en daarom onze mediaan is. De mediaan wordt ook wel de tweede kwartiel.
3 Zoek de mediaan van de dataset. De mediaan is het middelste cijfer in een geordende gegevensset. (Daarom hebben we alle getallen in stap 2 opgesteld.) Voor de gegevensset in ons voorbeeld is 3 het getal dat precies in het midden ligt en daarom onze mediaan is. De mediaan wordt ook wel de tweede kwartiel.  4 Zoek het eerste en derde kwartiel. We hebben het tweede kwartiel van de dataset al gevonden, onze mediaan. Nu moeten we de mediaan van de onderste helft van de dataset vinden; in ons voorbeeld zou het de mediaan zijn van de twee nummers naar de links van 3. De mediaan van 1 en 2 is (1 + 2) / 2 = 1,5. Doe hetzelfde om de mediaan van de twee nummers te vinden in de rechts van 3. (4 + 5) / 2 = 4.5.
4 Zoek het eerste en derde kwartiel. We hebben het tweede kwartiel van de dataset al gevonden, onze mediaan. Nu moeten we de mediaan van de onderste helft van de dataset vinden; in ons voorbeeld zou het de mediaan zijn van de twee nummers naar de links van 3. De mediaan van 1 en 2 is (1 + 2) / 2 = 1,5. Doe hetzelfde om de mediaan van de twee nummers te vinden in de rechts van 3. (4 + 5) / 2 = 4.5.  5 Teken een plotlijn. Dit moet lang genoeg zijn om al uw gegevens te bevatten, plus een beetje extra aan elke kant. Zorg ervoor dat de nummers met gelijke intervallen worden geplaatst. Als u decimalen gebruikt, zoals 4.5 en 1.5, moet u deze ook labelen.
5 Teken een plotlijn. Dit moet lang genoeg zijn om al uw gegevens te bevatten, plus een beetje extra aan elke kant. Zorg ervoor dat de nummers met gelijke intervallen worden geplaatst. Als u decimalen gebruikt, zoals 4.5 en 1.5, moet u deze ook labelen.  7 Maak een doos door horizontale lijnen te tekenen die de kwartielen verbinden. Verbind het bovenste of het eerste kwartiel met de bovenkant van het derde kwartiel en doorloop het tweede kwartiel. Verbind de onderkant van het eerste kwartiel met de onderkant van het derde kwartiel en zorg ervoor dat je door het tweede kwartiel gaat.
7 Maak een doos door horizontale lijnen te tekenen die de kwartielen verbinden. Verbind het bovenste of het eerste kwartiel met de bovenkant van het derde kwartiel en doorloop het tweede kwartiel. Verbind de onderkant van het eerste kwartiel met de onderkant van het derde kwartiel en zorg ervoor dat je door het tweede kwartiel gaat.  8 Markeer uw uitschieters. Zoek de kleinste en vervolgens de grootste cijfers in uw gegevensset en markeer deze op de plotlijn. Markeer deze punten met een kleine stip. In het geval van ons voorbeeld is de onderste uitbijter 1 en de bovenste uitbijter 5.
8 Markeer uw uitschieters. Zoek de kleinste en vervolgens de grootste cijfers in uw gegevensset en markeer deze op de plotlijn. Markeer deze punten met een kleine stip. In het geval van ons voorbeeld is de onderste uitbijter 1 en de bovenste uitbijter 5.  9 Verbind uw uitbijters met de doos met een horizontale lijn. De rechte lijn die de uitbijters verbindt, wordt informeel de "snorharen" van de doos en de snorharenplot genoemd.
9 Verbind uw uitbijters met de doos met een horizontale lijn. De rechte lijn die de uitbijters verbindt, wordt informeel de "snorharen" van de doos en de snorharenplot genoemd.