De IQR is het "interkwartielbereik" van een gegevensverzameling. Het wordt gebruikt in statistische analyse om conclusies te trekken over een reeks cijfers. De IQR heeft vaak de voorkeur boven het bereik omdat de meeste uitschieters worden uitgesloten. Lees verder om te leren hoe u de IQR kunt vinden!
Methode één van de drie:
De IQR begrijpen
-
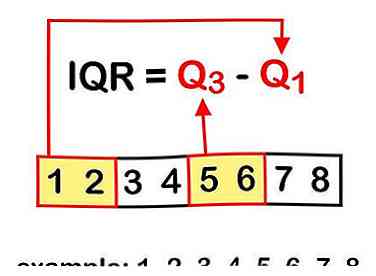 1 Weet hoe de IQR wordt gebruikt. In wezen is het een manier om de verspreiding of "verspreiding" van een reeks getallen te begrijpen.[1] Het interkwartielbereik wordt gedefinieerd als het verschil tussen het bovenste kwartiel (de hoogste 25%) en het onderste kwartiel (de laagste 25%) van een gegevensverzameling. Het onderste kwartiel wordt meestal geschreven als Q1 en het bovenste kwartiel is Q3 - wat technisch gezien het halverwege punt van de gegevensset Q2 zou zijn, en het hoogste punt Q4.[2]
1 Weet hoe de IQR wordt gebruikt. In wezen is het een manier om de verspreiding of "verspreiding" van een reeks getallen te begrijpen.[1] Het interkwartielbereik wordt gedefinieerd als het verschil tussen het bovenste kwartiel (de hoogste 25%) en het onderste kwartiel (de laagste 25%) van een gegevensverzameling. Het onderste kwartiel wordt meestal geschreven als Q1 en het bovenste kwartiel is Q3 - wat technisch gezien het halverwege punt van de gegevensset Q2 zou zijn, en het hoogste punt Q4.[2] -
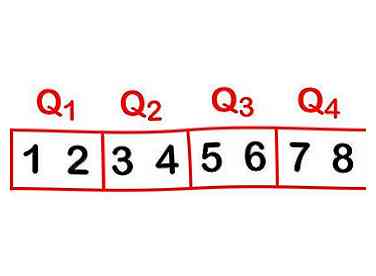 2 Kwartielen begrijpen. Visualiseer een kwartiel en snijd een lijst met getallen in vier gelijke delen. Elk van deze delen is een 'kwartiel'.[3] Overweeg de set: 1, 2, 3, 4, 5, 6, 7, 8.
2 Kwartielen begrijpen. Visualiseer een kwartiel en snijd een lijst met getallen in vier gelijke delen. Elk van deze delen is een 'kwartiel'.[3] Overweeg de set: 1, 2, 3, 4, 5, 6, 7, 8. - 1 en 2 zijn het eerste kwartiel, of Q1
- 3 en 4 zijn het tweede kwartiel, of Q2
- 5 en 6 zijn het derde kwartiel, of Q3
- 7 en 8 zijn het vierde kwartiel of Q4
-
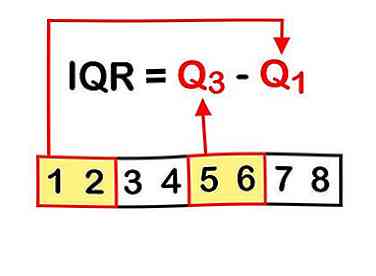 3 Leer de formule. Om het verschil tussen het bovenste en onderste kwartiel te vinden, moet u het 25e percentiel van het 75e percentiel aftrekken. De formule is geschreven als: Q3 - Q1 = IQR.[4]
3 Leer de formule. Om het verschil tussen het bovenste en onderste kwartiel te vinden, moet u het 25e percentiel van het 75e percentiel aftrekken. De formule is geschreven als: Q3 - Q1 = IQR.[4]
Methode twee van drie:
De dataset ordenen
-
 1 Verzamel uw gegevens. Als u dit voor een klas leert en een toets aflegt, krijgt u mogelijk een kant-en-klare reeks cijfers, bijvoorbeeld 1, 4, 5, 7, 10. Dit is uw dataset - de nummers waarmee u gaat werken. Het is echter mogelijk dat u de nummers zelf moet rangschikken in een soort tabel- of woordenprobleem. Zorg ervoor dat elk nummer naar hetzelfde soort dingen verwijst: bijvoorbeeld het aantal eieren in elk nest van een bepaalde vogelpopulatie of het aantal parkeerplaatsen dat aan elk huis op een bepaald blok is bevestigd.[5]
1 Verzamel uw gegevens. Als u dit voor een klas leert en een toets aflegt, krijgt u mogelijk een kant-en-klare reeks cijfers, bijvoorbeeld 1, 4, 5, 7, 10. Dit is uw dataset - de nummers waarmee u gaat werken. Het is echter mogelijk dat u de nummers zelf moet rangschikken in een soort tabel- of woordenprobleem. Zorg ervoor dat elk nummer naar hetzelfde soort dingen verwijst: bijvoorbeeld het aantal eieren in elk nest van een bepaalde vogelpopulatie of het aantal parkeerplaatsen dat aan elk huis op een bepaald blok is bevestigd.[5] -
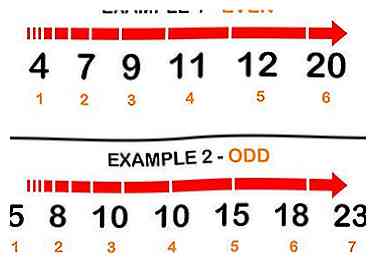 2 Organiseer uw dataset in oplopende volgorde. Met andere woorden: rangschik de getallen van laag naar hoog. Houd rekening met de volgende voorbeelden.
2 Organiseer uw dataset in oplopende volgorde. Met andere woorden: rangschik de getallen van laag naar hoog. Houd rekening met de volgende voorbeelden. - Even aantal gegevensvoorbeeld (set A): 4 7 9 11 12 20
- Oneven aantal gegevensvoorbeeld (set B): 5 8 10 10 15 18 23
-
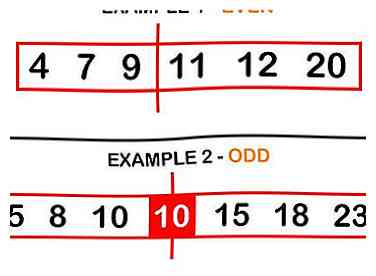 3 Deel de gegevens in twee. Zoek hiervoor het middelpunt van uw gegevens: het aantal of de cijfers in het midden van de set. Als u een oneven aantal nummers hebt, kiest u het exacte middelste nummer. Als u een even aantal getallen hebt, zal het middelpunt rusten tussen de twee middelste cijfers.
3 Deel de gegevens in twee. Zoek hiervoor het middelpunt van uw gegevens: het aantal of de cijfers in het midden van de set. Als u een oneven aantal nummers hebt, kiest u het exacte middelste nummer. Als u een even aantal getallen hebt, zal het middelpunt rusten tussen de twee middelste cijfers. - Zelfs een voorbeeld (Set A), waarbij het middelpunt tussen 9 en 11 ligt: 4 7 9 | 11 12 20
- Oneven voorbeeld (Set B), waarin (10) het middelpunt is: 5 8 10 (10) 15 18 23
Methode drie van drie:
De IQR berekenen
-
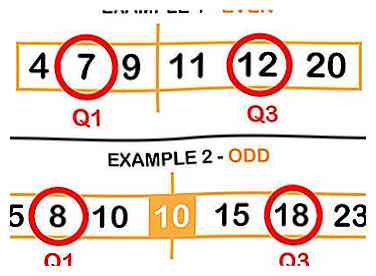 1 Zoek de mediaan van de onderste en bovenste helft van uw gegevens. De mediaan is het 'middelpunt' of het getal dat halverwege een reeks is.[6] In dit geval zoekt u niet naar het middelpunt van de gehele set, maar naar de relatieve middelpunten van de bovenste en onderste subsets. Als u een oneven aantal gegevens hebt, neemt u het middelste getal niet op. In Set B zou u bijvoorbeeld niet in een van de tienen voorkomen.[7]
1 Zoek de mediaan van de onderste en bovenste helft van uw gegevens. De mediaan is het 'middelpunt' of het getal dat halverwege een reeks is.[6] In dit geval zoekt u niet naar het middelpunt van de gehele set, maar naar de relatieve middelpunten van de bovenste en onderste subsets. Als u een oneven aantal gegevens hebt, neemt u het middelste getal niet op. In Set B zou u bijvoorbeeld niet in een van de tienen voorkomen.[7] - Zelfs een voorbeeld (set A):
- Mediaan van lagere helft = 7 (Q1)
- Mediaan van bovenhelft = 12 (Q3)
- Vreemd voorbeeld (set B):
- Mediaan van de onderste helft = 8 (Q1)
- Mediaan van bovenhelft = 18 (Q3)
- Zelfs een voorbeeld (set A):
-
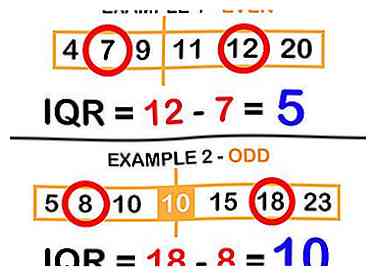 2 Trek Q3 - Q1 af om de IQR te bepalen. Nu weet je hoeveel getallen er liggen tussen het 25e percentiel en het 75e percentiel. U kunt dit gebruiken om te begrijpen hoe wijdverspreid de gegevens zijn. Als een toets bijvoorbeeld wordt gescoord uit 100 en de IQR van de scores 5 is, kunt u ervan uitgaan dat de meeste mensen die het hadden een vergelijkbaar begrip van het materiaal hadden, omdat het hoog-laag bereik niet erg groot is. Als de IQR van de testscores echter 30 is, vraag je je misschien af waarom sommige mensen zo hoog scoorden en anderen zo laag scoorden.
2 Trek Q3 - Q1 af om de IQR te bepalen. Nu weet je hoeveel getallen er liggen tussen het 25e percentiel en het 75e percentiel. U kunt dit gebruiken om te begrijpen hoe wijdverspreid de gegevens zijn. Als een toets bijvoorbeeld wordt gescoord uit 100 en de IQR van de scores 5 is, kunt u ervan uitgaan dat de meeste mensen die het hadden een vergelijkbaar begrip van het materiaal hadden, omdat het hoog-laag bereik niet erg groot is. Als de IQR van de testscores echter 30 is, vraag je je misschien af waarom sommige mensen zo hoog scoorden en anderen zo laag scoorden. - Zelfs een voorbeeld (set A): 12 - 7 = 5
- Oneven voorbeeld (Set B): 18 - 8 = 10
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Weet hoe de IQR wordt gebruikt. In wezen is het een manier om de verspreiding of "verspreiding" van een reeks getallen te begrijpen.[1] Het interkwartielbereik wordt gedefinieerd als het verschil tussen het bovenste kwartiel (de hoogste 25%) en het onderste kwartiel (de laagste 25%) van een gegevensverzameling. Het onderste kwartiel wordt meestal geschreven als Q1 en het bovenste kwartiel is Q3 - wat technisch gezien het halverwege punt van de gegevensset Q2 zou zijn, en het hoogste punt Q4.[2]
1 Weet hoe de IQR wordt gebruikt. In wezen is het een manier om de verspreiding of "verspreiding" van een reeks getallen te begrijpen.[1] Het interkwartielbereik wordt gedefinieerd als het verschil tussen het bovenste kwartiel (de hoogste 25%) en het onderste kwartiel (de laagste 25%) van een gegevensverzameling. Het onderste kwartiel wordt meestal geschreven als Q1 en het bovenste kwartiel is Q3 - wat technisch gezien het halverwege punt van de gegevensset Q2 zou zijn, en het hoogste punt Q4.[2] 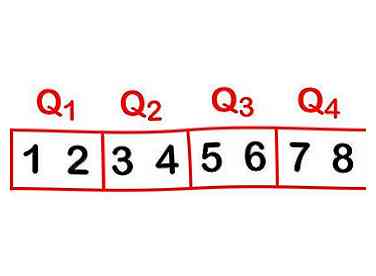 2 Kwartielen begrijpen. Visualiseer een kwartiel en snijd een lijst met getallen in vier gelijke delen. Elk van deze delen is een 'kwartiel'.[3] Overweeg de set: 1, 2, 3, 4, 5, 6, 7, 8.
2 Kwartielen begrijpen. Visualiseer een kwartiel en snijd een lijst met getallen in vier gelijke delen. Elk van deze delen is een 'kwartiel'.[3] Overweeg de set: 1, 2, 3, 4, 5, 6, 7, 8.  3 Leer de formule. Om het verschil tussen het bovenste en onderste kwartiel te vinden, moet u het 25e percentiel van het 75e percentiel aftrekken. De formule is geschreven als: Q3 - Q1 = IQR.[4]
3 Leer de formule. Om het verschil tussen het bovenste en onderste kwartiel te vinden, moet u het 25e percentiel van het 75e percentiel aftrekken. De formule is geschreven als: Q3 - Q1 = IQR.[4]  1 Verzamel uw gegevens. Als u dit voor een klas leert en een toets aflegt, krijgt u mogelijk een kant-en-klare reeks cijfers, bijvoorbeeld 1, 4, 5, 7, 10. Dit is uw dataset - de nummers waarmee u gaat werken. Het is echter mogelijk dat u de nummers zelf moet rangschikken in een soort tabel- of woordenprobleem. Zorg ervoor dat elk nummer naar hetzelfde soort dingen verwijst: bijvoorbeeld het aantal eieren in elk nest van een bepaalde vogelpopulatie of het aantal parkeerplaatsen dat aan elk huis op een bepaald blok is bevestigd.[5]
1 Verzamel uw gegevens. Als u dit voor een klas leert en een toets aflegt, krijgt u mogelijk een kant-en-klare reeks cijfers, bijvoorbeeld 1, 4, 5, 7, 10. Dit is uw dataset - de nummers waarmee u gaat werken. Het is echter mogelijk dat u de nummers zelf moet rangschikken in een soort tabel- of woordenprobleem. Zorg ervoor dat elk nummer naar hetzelfde soort dingen verwijst: bijvoorbeeld het aantal eieren in elk nest van een bepaalde vogelpopulatie of het aantal parkeerplaatsen dat aan elk huis op een bepaald blok is bevestigd.[5]  2 Organiseer uw dataset in oplopende volgorde. Met andere woorden: rangschik de getallen van laag naar hoog. Houd rekening met de volgende voorbeelden.
2 Organiseer uw dataset in oplopende volgorde. Met andere woorden: rangschik de getallen van laag naar hoog. Houd rekening met de volgende voorbeelden.  3 Deel de gegevens in twee. Zoek hiervoor het middelpunt van uw gegevens: het aantal of de cijfers in het midden van de set. Als u een oneven aantal nummers hebt, kiest u het exacte middelste nummer. Als u een even aantal getallen hebt, zal het middelpunt rusten tussen de twee middelste cijfers.
3 Deel de gegevens in twee. Zoek hiervoor het middelpunt van uw gegevens: het aantal of de cijfers in het midden van de set. Als u een oneven aantal nummers hebt, kiest u het exacte middelste nummer. Als u een even aantal getallen hebt, zal het middelpunt rusten tussen de twee middelste cijfers.  1 Zoek de mediaan van de onderste en bovenste helft van uw gegevens. De mediaan is het 'middelpunt' of het getal dat halverwege een reeks is.[6] In dit geval zoekt u niet naar het middelpunt van de gehele set, maar naar de relatieve middelpunten van de bovenste en onderste subsets. Als u een oneven aantal gegevens hebt, neemt u het middelste getal niet op. In Set B zou u bijvoorbeeld niet in een van de tienen voorkomen.[7]
1 Zoek de mediaan van de onderste en bovenste helft van uw gegevens. De mediaan is het 'middelpunt' of het getal dat halverwege een reeks is.[6] In dit geval zoekt u niet naar het middelpunt van de gehele set, maar naar de relatieve middelpunten van de bovenste en onderste subsets. Als u een oneven aantal gegevens hebt, neemt u het middelste getal niet op. In Set B zou u bijvoorbeeld niet in een van de tienen voorkomen.[7]  2 Trek Q3 - Q1 af om de IQR te bepalen. Nu weet je hoeveel getallen er liggen tussen het 25e percentiel en het 75e percentiel. U kunt dit gebruiken om te begrijpen hoe wijdverspreid de gegevens zijn. Als een toets bijvoorbeeld wordt gescoord uit 100 en de IQR van de scores 5 is, kunt u ervan uitgaan dat de meeste mensen die het hadden een vergelijkbaar begrip van het materiaal hadden, omdat het hoog-laag bereik niet erg groot is. Als de IQR van de testscores echter 30 is, vraag je je misschien af waarom sommige mensen zo hoog scoorden en anderen zo laag scoorden.
2 Trek Q3 - Q1 af om de IQR te bepalen. Nu weet je hoeveel getallen er liggen tussen het 25e percentiel en het 75e percentiel. U kunt dit gebruiken om te begrijpen hoe wijdverspreid de gegevens zijn. Als een toets bijvoorbeeld wordt gescoord uit 100 en de IQR van de scores 5 is, kunt u ervan uitgaan dat de meeste mensen die het hadden een vergelijkbaar begrip van het materiaal hadden, omdat het hoog-laag bereik niet erg groot is. Als de IQR van de testscores echter 30 is, vraag je je misschien af waarom sommige mensen zo hoog scoorden en anderen zo laag scoorden.