Factorieën worden vaak gebruikt bij het berekenen van de waarschijnlijkheid en permutaties, of mogelijke orden van gebeurtenissen.[1] Een faculteit wordt aangeduid met a teken, en het betekent het vermenigvuldigen van alle getallen die aflopen van het faculteitnummer. Als je eenmaal begrijpt wat een faculteit is, is het eenvoudig te berekenen, vooral met behulp van een wetenschappelijke rekenmachine.
Methode één van de drie:
Een factorie berekenen
-
 1 Bepaal het aantal waarvoor u de factorie berekent. Een faculteit wordt aangeduid met een positief geheel getal en een uitroepteken.
1 Bepaal het aantal waarvoor u de factorie berekent. Een faculteit wordt aangeduid met een positief geheel getal en een uitroepteken. - Als u bijvoorbeeld de faculteit voor 5 moet berekenen, ziet u .
-
 2 Schrijf de reeks getallen die moet worden vermenigvuldigd. Een faculteit is eenvoudigweg het vermenigvuldigen van de natuurlijke getallen die opeenvolgend van het faculteitgetal aflopen, naar beneden naar 1.[2] Formeel gesproken, , waar is gelijk aan een positief geheel getal.[3]
2 Schrijf de reeks getallen die moet worden vermenigvuldigd. Een faculteit is eenvoudigweg het vermenigvuldigen van de natuurlijke getallen die opeenvolgend van het faculteitgetal aflopen, naar beneden naar 1.[2] Formeel gesproken, , waar is gelijk aan een positief geheel getal.[3] - Bijvoorbeeld als u aan het rekenen bent , zou je berekenen of, eenvoudiger gezegd: .
-
 3 Vermenigvuldig de getallen samen. Je kunt snel een faculteit berekenen met een wetenschappelijke rekenmachine, die een a zou moeten hebben teken. Als u met de hand wilt berekenen, om het gemakkelijker te maken, moet u eerst zoeken naar factoren die zich vermenigvuldigen tot gelijk aan 10.[4] Natuurlijk kunt u ook de 1 negeren, omdat elk getal vermenigvuldigd met 1 gelijk is aan dat aantal.
3 Vermenigvuldig de getallen samen. Je kunt snel een faculteit berekenen met een wetenschappelijke rekenmachine, die een a zou moeten hebben teken. Als u met de hand wilt berekenen, om het gemakkelijker te maken, moet u eerst zoeken naar factoren die zich vermenigvuldigen tot gelijk aan 10.[4] Natuurlijk kunt u ook de 1 negeren, omdat elk getal vermenigvuldigd met 1 gelijk is aan dat aantal. - Bijvoorbeeld voor computergebruik , negeer de 1 en bereken eerst . Nu rest je alleen nog . Sinds , dat weet je .
Methode twee van drie:
Een factorie vereenvoudigen
-
 1 Bepaal de uitdrukking die u vereenvoudigt. Vaak wordt dit als een breuk vermeld.
1 Bepaal de uitdrukking die u vereenvoudigt. Vaak wordt dit als een breuk vermeld. - U moet bijvoorbeeld mogelijk vereenvoudigen .
-
 2 Schrijf de factoren van elke faculteit op. Sinds de faculteit is een factor van elke faculteit groter dan het, om te vereenvoudigen, moet je op zoek naar factoren die je kunt annuleren.[5] Dit is eenvoudig te doen als je elke term opschrijft.[6]
2 Schrijf de factoren van elke faculteit op. Sinds de faculteit is een factor van elke faculteit groter dan het, om te vereenvoudigen, moet je op zoek naar factoren die je kunt annuleren.[5] Dit is eenvoudig te doen als je elke term opschrijft.[6] - Bijvoorbeeld als vereenvoudiging , herschrijf als
-
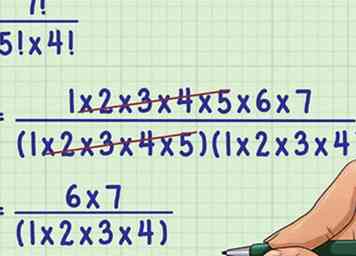 3 Annuleer alle termen die horen bij de teller en de noemer.[7] Dit vereenvoudigt het aantal overgebleven nummers dat u moet vermenigvuldigen.
3 Annuleer alle termen die horen bij de teller en de noemer.[7] Dit vereenvoudigt het aantal overgebleven nummers dat u moet vermenigvuldigen. - Bijvoorbeeld sinds is een factor van , je kunt annuleren van de teller en noemer:
- Bijvoorbeeld sinds is een factor van , je kunt annuleren van de teller en noemer:
-
 4 Voer de berekeningen uit. Vereenvoudig indien mogelijk. Dit geeft je de laatste, vereenvoudigde expressie.
4 Voer de berekeningen uit. Vereenvoudig indien mogelijk. Dit geeft je de laatste, vereenvoudigde expressie. - Bijvoorbeeld:
Zo, vereenvoudigd is .
- Bijvoorbeeld:
Methode drie van drie:
Factorfacturale problemen doen
-
 1 Evalueer de uitdrukking 8!.
1 Evalueer de uitdrukking 8!. - Als u een wetenschappelijke rekenmachine gebruikt, drukt u op sleutel, gevolgd door de sleutel.
- Als u met de hand schrijft, noteer dan de factoren die vermenigvuldigd moeten worden:
- Negeer de 1:
- Uittrekken :
- Groepeer eerst alle andere gemakkelijk vermenigvuldigde getallen en vermenigvuldig vervolgens alle producten samen:
Zo, .
-
 2 Vereenvoudig de uitdrukking: .
2 Vereenvoudig de uitdrukking: . - Schrijf de factoren van elke faculteit op:
- Algemene voorwaarden voor de teller en noemer annuleren:
- Maak de berekeningen:
Dus de uitdrukking vereenvoudigt tot .
- Schrijf de factoren van elke faculteit op:
-
 3 Probeer het volgende probleem. Je hebt 6 schilderijen die je op een rij aan je muur wilt laten zien. Hoeveel verschillende manieren kun je de schilderijen bestellen?
3 Probeer het volgende probleem. Je hebt 6 schilderijen die je op een rij aan je muur wilt laten zien. Hoeveel verschillende manieren kun je de schilderijen bestellen? - Omdat u op zoek bent naar verschillende manieren om objecten te bestellen, kunt u eenvoudigweg oplossen door de faculteit te vinden voor het aantal objecten.
- Het aantal mogelijke arrangementen voor 6 schilderijen die op een rij zijn opgehangen, kan worden opgelost door te vinden .
- Als u een wetenschappelijke rekenmachine gebruikt, drukt u op sleutel, gevolgd door de sleutel.
- Als u met de hand schrijft, noteer dan de factoren die vermenigvuldigd moeten worden:
- Negeer de 1:
- Uittrekken :
- Groepeer eerst alle andere gemakkelijk vermenigvuldigde getallen en vermenigvuldig vervolgens alle producten samen:
Dus 6 schilderijen op een rij kunnen 720 verschillende manieren worden besteld.
-
 4 Probeer het volgende probleem. Je hebt 6 schilderijen. U wilt 3 van hen op een rij aan uw muur weergeven. Hoeveel verschillende manieren kun je 3 van de schilderijen bestellen?
4 Probeer het volgende probleem. Je hebt 6 schilderijen. U wilt 3 van hen op een rij aan uw muur weergeven. Hoeveel verschillende manieren kun je 3 van de schilderijen bestellen? - Omdat je 6 verschillende schilderijen hebt, maar je kiest er maar 3, hoef je alleen de eerste 3 getallen in de reeks te vermenigvuldigen met de faculteit van 6. Je kunt ook de formule gebruiken , waar is gelijk aan het aantal objecten waaruit u kiest, en is gelijk aan het aantal objecten dat u gebruikt. Deze formule werkt alleen als je geen herhalingen hebt (een object kan niet meer dan één keer worden gekozen) en de volgorde is van belang (dat wil zeggen, je wilt weten op hoeveel verschillende manieren dingen kunnen worden besteld).[8]
- Het aantal mogelijke arrangementen voor 3 schilderijen gekozen uit 6 en achter elkaar opgehangen kan worden opgelost door te vinden .
- Trek de getallen in de noemer af:
- Schrijf de factoren van elke faculteit:
- Algemene voorwaarden voor de teller en noemer annuleren:
- Maak de berekeningen:
Dus, 3 schilderijen gekozen uit 6 kunnen op 120 verschillende manieren worden besteld als ze op een rij worden gehangen.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Bepaal het aantal waarvoor u de factorie berekent. Een faculteit wordt aangeduid met een positief geheel getal en een uitroepteken.
1 Bepaal het aantal waarvoor u de factorie berekent. Een faculteit wordt aangeduid met een positief geheel getal en een uitroepteken.  2 Schrijf de reeks getallen die moet worden vermenigvuldigd. Een faculteit is eenvoudigweg het vermenigvuldigen van de natuurlijke getallen die opeenvolgend van het faculteitgetal aflopen, naar beneden naar 1.[2] Formeel gesproken,
2 Schrijf de reeks getallen die moet worden vermenigvuldigd. Een faculteit is eenvoudigweg het vermenigvuldigen van de natuurlijke getallen die opeenvolgend van het faculteitgetal aflopen, naar beneden naar 1.[2] Formeel gesproken,  3 Vermenigvuldig de getallen samen. Je kunt snel een faculteit berekenen met een wetenschappelijke rekenmachine, die een a zou moeten hebben
3 Vermenigvuldig de getallen samen. Je kunt snel een faculteit berekenen met een wetenschappelijke rekenmachine, die een a zou moeten hebben  1 Bepaal de uitdrukking die u vereenvoudigt. Vaak wordt dit als een breuk vermeld.
1 Bepaal de uitdrukking die u vereenvoudigt. Vaak wordt dit als een breuk vermeld.  2 Schrijf de factoren van elke faculteit op. Sinds de faculteit
2 Schrijf de factoren van elke faculteit op. Sinds de faculteit 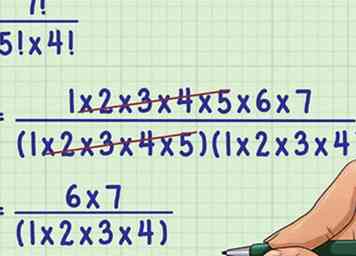 3 Annuleer alle termen die horen bij de teller en de noemer.[7] Dit vereenvoudigt het aantal overgebleven nummers dat u moet vermenigvuldigen.
3 Annuleer alle termen die horen bij de teller en de noemer.[7] Dit vereenvoudigt het aantal overgebleven nummers dat u moet vermenigvuldigen.  4 Voer de berekeningen uit. Vereenvoudig indien mogelijk. Dit geeft je de laatste, vereenvoudigde expressie.
4 Voer de berekeningen uit. Vereenvoudig indien mogelijk. Dit geeft je de laatste, vereenvoudigde expressie.  1 Evalueer de uitdrukking 8!.
1 Evalueer de uitdrukking 8!.  2 Vereenvoudig de uitdrukking:
2 Vereenvoudig de uitdrukking:  3 Probeer het volgende probleem. Je hebt 6 schilderijen die je op een rij aan je muur wilt laten zien. Hoeveel verschillende manieren kun je de schilderijen bestellen?
3 Probeer het volgende probleem. Je hebt 6 schilderijen die je op een rij aan je muur wilt laten zien. Hoeveel verschillende manieren kun je de schilderijen bestellen?  4 Probeer het volgende probleem. Je hebt 6 schilderijen. U wilt 3 van hen op een rij aan uw muur weergeven. Hoeveel verschillende manieren kun je 3 van de schilderijen bestellen?
4 Probeer het volgende probleem. Je hebt 6 schilderijen. U wilt 3 van hen op een rij aan uw muur weergeven. Hoeveel verschillende manieren kun je 3 van de schilderijen bestellen?