In statistieken, de mode van een reeks getallen is de nummer dat het vaakst in de set voorkomt. Een dataset hoeft niet per se maar één modus te hebben - als twee of meer waarden 'gebonden' zijn om de meest voorkomende te zijn, kan worden gezegd dat de set bimodale of multimodale, met andere woorden, alle van de meest voorkomende waarden zijn de modi van de set. Zie Stap 1 hieronder om aan de slag te gaan voor een gedetailleerd overzicht van het proces van het bepalen van de modus (en) van een dataset.
Methode één van de twee:
De modus van een dataset zoeken
-
 1 Schrijf de cijfers in uw dataset. Modi worden meestal ontleend aan verzamelingen statistische gegevenspunten of lijsten met numerieke waarden. Om een modus te vinden, hebt u dus een dataset nodig om deze te vinden. Het is moeilijk om modusberekeningen mentaal uit te voeren voor alle, behalve de kleinste datasets, dus in de meeste gevallen is het verstandig om te beginnen met het schrijven (of typen) van je gegevens. Als u met papier en een potlood werkt, volstaat het om de waarden van uw dataset achter elkaar te schrijven, terwijl u, als u een computer gebruikt, een spreadsheetprogramma wilt gebruiken om het proces te stroomlijnen.
1 Schrijf de cijfers in uw dataset. Modi worden meestal ontleend aan verzamelingen statistische gegevenspunten of lijsten met numerieke waarden. Om een modus te vinden, hebt u dus een dataset nodig om deze te vinden. Het is moeilijk om modusberekeningen mentaal uit te voeren voor alle, behalve de kleinste datasets, dus in de meeste gevallen is het verstandig om te beginnen met het schrijven (of typen) van je gegevens. Als u met papier en een potlood werkt, volstaat het om de waarden van uw dataset achter elkaar te schrijven, terwijl u, als u een computer gebruikt, een spreadsheetprogramma wilt gebruiken om het proces te stroomlijnen. - Het proces van het vinden van de modus van een gegevensset is gemakkelijker te begrijpen door het volgen van een voorbeeldprobleem. Laten we in deze sectie deze reeks waarden gebruiken voor de doeleinden van ons voorbeeld: 18, 21, 11, 21, 15, 19, 17, 21, 17. In de volgende paar stappen zullen we de modus van deze set vinden.
-
 2 Bestel de nummers van klein naar groot. Vervolgens is het vaak een verstandig idee om de waarden van uw gegevensset zo te sorteren dat ze in stijgende volgorde staan. Hoewel dit niet strikt vereist is, maakt het het proces van het vinden van de modus gemakkelijker omdat het identieke waarden naast elkaar groepeert. Voor grote gegevenssets kan het praktisch een noodzaak zijn, omdat het sorteren van lange lijsten met waarden en het bijhouden van mentale overeenkomsten van hoe vaak elk getal in de lijst voorkomt, moeilijk is en tot fouten kan leiden.
2 Bestel de nummers van klein naar groot. Vervolgens is het vaak een verstandig idee om de waarden van uw gegevensset zo te sorteren dat ze in stijgende volgorde staan. Hoewel dit niet strikt vereist is, maakt het het proces van het vinden van de modus gemakkelijker omdat het identieke waarden naast elkaar groepeert. Voor grote gegevenssets kan het praktisch een noodzaak zijn, omdat het sorteren van lange lijsten met waarden en het bijhouden van mentale overeenkomsten van hoe vaak elk getal in de lijst voorkomt, moeilijk is en tot fouten kan leiden. - Als u met papier en een potlood werkt, kan het herschrijven op de lange termijn tijd besparen. Scan de set met getallen voor het laagste nummer en kruis deze af in de eerste dataset en schrijf deze opnieuw op in uw nieuwe dataset. Herhaal dit voor het op een na laagste getal, de derde laagste, enzovoort, en zorg ervoor dat elk nummer net zo vaak wordt geschreven als het voorkomt in de oorspronkelijke gegevensset.
- Met een computer zijn uw opties uitgebreider - bijvoorbeeld, de meeste spreadsheetprogramma's hebben de optie om lijsten met waarden opnieuw te rangschikken van minst naar beste met slechts een paar klikken.
- In ons voorbeeld moet na het opnieuw ordenen de nieuwe lijst met waarden luiden: 11, 15, 17, 17, 18, 19, 21, 21, 21.
-
 3 Tel het aantal keren dat elk nummer wordt herhaald. Tel hierna het aantal keren dat elk nummer in de set wordt weergegeven. Zoek naar de waarde die het meest voorkomt in de dataset. Voor relatief kleine gegevenssets met punten die in oplopende volgorde zijn gerangschikt, is dit meestal een kwestie van het vinden van de grootste "cluster" van identieke waarden en het tellen van het aantal keren.
3 Tel het aantal keren dat elk nummer wordt herhaald. Tel hierna het aantal keren dat elk nummer in de set wordt weergegeven. Zoek naar de waarde die het meest voorkomt in de dataset. Voor relatief kleine gegevenssets met punten die in oplopende volgorde zijn gerangschikt, is dit meestal een kwestie van het vinden van de grootste "cluster" van identieke waarden en het tellen van het aantal keren. - Als u met een potlood en papier werkt, probeer dan het aantal keren dat elke waarde boven elke cluster van identieke nummers voorkomt, bij te houden om uw tellingen bij te houden. Als u een spreadsheetprogramma op een computer gebruikt, kunt u hetzelfde doen door uw totalen in aangrenzende cellen te schrijven of door een van de programma-opties voor het tellen van gegevenspunten te gebruiken.
- In ons voorbeeld (11, 15, 17, 17, 18, 19, 21, 21, 21), komt 11 één keer voor, 15 één keer, 17 twee keer, 18 één keer, 19 één keer, en 21 komt drie keer voor. 21 is de meest voorkomende waarde in deze dataset.
-
 4 Identificeer de waarde (of waarden) die het meest voorkomen. Als u weet hoeveel keer elke waarde voorkomt in uw gegevensset, zoekt u de waarde die het grootste aantal keren voorkomt. Dit is de modus van uw dataset. Let daar op er kan meer dan één modus in een dataset zijn. Als de twee waarden gelijk zijn aan de meest voorkomende waarden in de set, kan worden gesteld dat de gegevensset dat is bimodale, terwijl als drie waarden zijn gekoppeld, de set is trimodale, enzovoort.
4 Identificeer de waarde (of waarden) die het meest voorkomen. Als u weet hoeveel keer elke waarde voorkomt in uw gegevensset, zoekt u de waarde die het grootste aantal keren voorkomt. Dit is de modus van uw dataset. Let daar op er kan meer dan één modus in een dataset zijn. Als de twee waarden gelijk zijn aan de meest voorkomende waarden in de set, kan worden gesteld dat de gegevensset dat is bimodale, terwijl als drie waarden zijn gekoppeld, de set is trimodale, enzovoort. - In onze voorbeeldset (11, 15, 17, 17, 18, 19, 21, 21, 21), omdat 21 vaker voorkomt dan enige andere waarde, 21 is de modus.
- Als een waarde naast 21 had ook kwam drie keer voor (bijvoorbeeld als er nog 17 in de dataset waren), 21 en dit andere nummer wel beide de modus zijn.
-
 5 Verwar de modus van een gegevensset niet met het gemiddelde of de mediaan. Drie statistische concepten die vaak samen worden besproken, zijn middelen, medianen en modi. Omdat deze concepten allemaal hetzelfde klinkende namen hebben en omdat voor een enkele gegevensset soms een enkele waarde kan zijn meer dan een van deze dingen is het gemakkelijk om ze te verwarren. Ongeacht of de modus van de dataset ook mediaan of gemiddeld is, het is belangrijk om te begrijpen dat deze drie concepten volledig onafhankelijk van elkaar zijn. Zie hieronder:
5 Verwar de modus van een gegevensset niet met het gemiddelde of de mediaan. Drie statistische concepten die vaak samen worden besproken, zijn middelen, medianen en modi. Omdat deze concepten allemaal hetzelfde klinkende namen hebben en omdat voor een enkele gegevensset soms een enkele waarde kan zijn meer dan een van deze dingen is het gemakkelijk om ze te verwarren. Ongeacht of de modus van de dataset ook mediaan of gemiddeld is, het is belangrijk om te begrijpen dat deze drie concepten volledig onafhankelijk van elkaar zijn. Zie hieronder: - Een dataset is gemiddelde is het gemiddelde. Om het gemiddelde te vinden, optelt u alle waarden in de gegevensset en deelt u vervolgens het aantal waarden in de set. Voor onze voorbeeldgegevensverzameling (11, 15, 17, 17, 18, 19, 21, 21, 21) zou het gemiddelde bijvoorbeeld 11 + 15 + 17 + 17 + 18 + 19 + 21 + 21 + zijn 21 = 160/9 = 17.78. Merk op dat we de som van de waarden met 9 hebben verdeeld omdat er in de dataset in totaal 9 waarden zijn.

- Een dataset is mediaan- is het "middelste getal" dat de lagere en hogere waarden van een gegevensset scheidt in twee gelijke helften. Bijvoorbeeld in onze voorbeeldgegevensverzameling (11, 15, 17, 17, 18, 19, 21, 21, 21) 18 is de mediaan omdat het het middelste getal is - er zijn precies vier getallen hoger dan het getal en vier getallen lager dan het getal.Merk op dat als er een even aantal waarden in de gegevensverzameling zit, er geen enkele mediaan is. In deze gevallen wordt de mediaan meestal als het gemiddelde van de twee middelste getallen beschouwd.

- Een dataset is gemiddelde is het gemiddelde. Om het gemiddelde te vinden, optelt u alle waarden in de gegevensset en deelt u vervolgens het aantal waarden in de set. Voor onze voorbeeldgegevensverzameling (11, 15, 17, 17, 18, 19, 21, 21, 21) zou het gemiddelde bijvoorbeeld 11 + 15 + 17 + 17 + 18 + 19 + 21 + 21 + zijn 21 = 160/9 = 17.78. Merk op dat we de som van de waarden met 9 hebben verdeeld omdat er in de dataset in totaal 9 waarden zijn.
Methode twee van twee:
De modus vinden in speciale gevallen
-
 1 Erken dat er geen modus bestaat voor gegevenssets waarin elke waarde hetzelfde aantal keren voorkomt. Als de waarden in een bepaalde set allemaal hetzelfde aantal keren voorkomen, heeft de dataset geen modus omdat geen nummer vaker voorkomt dan andere. Gegevenssets waarin elke waarde één keer voorkomt, hebben bijvoorbeeld geen modus. Hetzelfde geldt voor datasets waarin elke waarde tweemaal, driemaal, enzovoort voorkomt.
1 Erken dat er geen modus bestaat voor gegevenssets waarin elke waarde hetzelfde aantal keren voorkomt. Als de waarden in een bepaalde set allemaal hetzelfde aantal keren voorkomen, heeft de dataset geen modus omdat geen nummer vaker voorkomt dan andere. Gegevenssets waarin elke waarde één keer voorkomt, hebben bijvoorbeeld geen modus. Hetzelfde geldt voor datasets waarin elke waarde tweemaal, driemaal, enzovoort voorkomt. - Als we onze voorbeeldgegevens instellen op 11, 15, 17, 18, 19, 21, zodat elke waarde maar één keer voorkomt, heeft de gegevensset nu geen modus. Hetzelfde is waar als we de gegevensverzameling zodanig wijzigen dat elke waarde twee keer voorkomt: 11, 11, 15, 15, 17, 17, 18, 18, 19, 19, 21, 21.
-
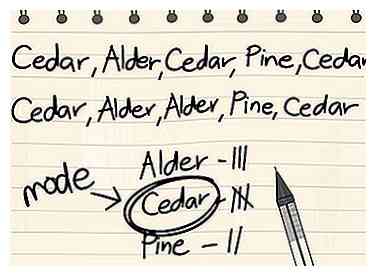 2 Erken dat modi voor niet-numerieke gegevenssets op dezelfde manier kunnen worden gevonden als voor numerieke gegevenssets. Over het algemeen zijn de meeste datasets kwantitatief - ze omgaan met gegevens in de vorm van getallen. Bepaalde gegevenssets hebben echter te maken met gegevens die niet in de vorm van getallen worden uitgedrukt. In deze gevallen kan worden gezegd dat de "modus" de enige waarde is die het meest voorkomt in de gegevensverzameling, net zoals bij numerieke gegevenssets.[1] In deze gevallen is het mogelijk om de modus te vinden terwijl het onmogelijk is om een zinvolle mediaan of gemiddelde waarde voor de gegevensset te vinden.
2 Erken dat modi voor niet-numerieke gegevenssets op dezelfde manier kunnen worden gevonden als voor numerieke gegevenssets. Over het algemeen zijn de meeste datasets kwantitatief - ze omgaan met gegevens in de vorm van getallen. Bepaalde gegevenssets hebben echter te maken met gegevens die niet in de vorm van getallen worden uitgedrukt. In deze gevallen kan worden gezegd dat de "modus" de enige waarde is die het meest voorkomt in de gegevensverzameling, net zoals bij numerieke gegevenssets.[1] In deze gevallen is het mogelijk om de modus te vinden terwijl het onmogelijk is om een zinvolle mediaan of gemiddelde waarde voor de gegevensset te vinden. - Laten we bijvoorbeeld zeggen dat een biologisch onderzoek de soort van elke boom in een klein lokaal deel bepaalt. De dataset voor de soorten bomen in het park is Cedar, Alder, Cedar, Pine, Cedar, Cedar, Alder, Alder, Pine, Cedar. Dit type gegevensset wordt a genoemd nominaal gegevensset omdat de gegevenspunten alleen door hun naam worden onderscheiden. In dit geval is de modus van de dataset Ceder omdat het het vaakst voorkomt (vijf keer in plaats van drie voor Alder en twee voor Pine).
- Merk op dat het voor de voorbeeldgegevensset hierboven onmogelijk is om een gemiddelde of mediaan te berekenen omdat de gegevenspunten geen numerieke waarde hebben.
-
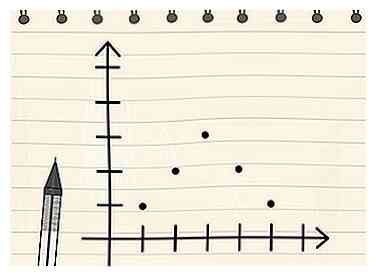 3 Erken dat voor unimodale symmetrische verdelingen de modus, het gemiddelde en de mediaan samenvallen. Zoals hierboven vermeld, is het mogelijk dat de modus, mediaan en / of gemiddelde in bepaalde gevallen overlappen. Selecteer in speciale gevallen waarin de dichtheidsfunctie van de gegevensverzameling een perfect symmetrische curve vormt met één modus (bijvoorbeeld de Gausse of "Bel-vormige" curve), de modus, het gemiddelde en de mediaan hebben allemaal dezelfde waarde. Omdat een distributiefunctie het relatieve voorkomen van gegevenspunten weergeeft, bevindt de modus zich uiteraard precies in het midden van een symmetrische verdelingskromme, omdat dit het hoogste punt in de grafiek is en overeenkomt met de meest gebruikelijke waarde. Omdat de dataset symmetrisch is, komt dit punt op de grafiek overeen met de mediaan - de middelste waarde in de gegevensset - en het gemiddelde - het gemiddelde van de gegevensverzameling.
3 Erken dat voor unimodale symmetrische verdelingen de modus, het gemiddelde en de mediaan samenvallen. Zoals hierboven vermeld, is het mogelijk dat de modus, mediaan en / of gemiddelde in bepaalde gevallen overlappen. Selecteer in speciale gevallen waarin de dichtheidsfunctie van de gegevensverzameling een perfect symmetrische curve vormt met één modus (bijvoorbeeld de Gausse of "Bel-vormige" curve), de modus, het gemiddelde en de mediaan hebben allemaal dezelfde waarde. Omdat een distributiefunctie het relatieve voorkomen van gegevenspunten weergeeft, bevindt de modus zich uiteraard precies in het midden van een symmetrische verdelingskromme, omdat dit het hoogste punt in de grafiek is en overeenkomt met de meest gebruikelijke waarde. Omdat de dataset symmetrisch is, komt dit punt op de grafiek overeen met de mediaan - de middelste waarde in de gegevensset - en het gemiddelde - het gemiddelde van de gegevensverzameling. - Laten we bijvoorbeeld de gegevensverzameling 1, 2, 2, 3, 3, 4, 4, 5 bekijken. Als we de verdeling van deze gegevensset zouden plotten, zouden we een symmetrische curve krijgen die een hoogte van 3 bereikt bij x = 3 en taps toelopen naar een hoogte van 1 bij x = 1 en x = 5. Omdat 3 de meest voorkomende waarde, het is de modus. Omdat de centrale 3 in de gegevensverzameling aan elke kant 4 waarden heeft, is er 3 ook de mediaan. Ten slotte werkt het gemiddelde van de gegevensverzameling uit op 1 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 = 27/9 = 3, wat betekent dat 3 is ook het gemiddelde.
- De uitzondering op deze regel is voor symmetrische gegevenssets met meer dan één modus - in dit geval omdat er slechts één mediaan en gemiddelde voor de gegevensverzameling kan zijn, zullen beide modi niet samenvallen met deze andere punten.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Schrijf de cijfers in uw dataset. Modi worden meestal ontleend aan verzamelingen statistische gegevenspunten of lijsten met numerieke waarden. Om een modus te vinden, hebt u dus een dataset nodig om deze te vinden. Het is moeilijk om modusberekeningen mentaal uit te voeren voor alle, behalve de kleinste datasets, dus in de meeste gevallen is het verstandig om te beginnen met het schrijven (of typen) van je gegevens. Als u met papier en een potlood werkt, volstaat het om de waarden van uw dataset achter elkaar te schrijven, terwijl u, als u een computer gebruikt, een spreadsheetprogramma wilt gebruiken om het proces te stroomlijnen.
1 Schrijf de cijfers in uw dataset. Modi worden meestal ontleend aan verzamelingen statistische gegevenspunten of lijsten met numerieke waarden. Om een modus te vinden, hebt u dus een dataset nodig om deze te vinden. Het is moeilijk om modusberekeningen mentaal uit te voeren voor alle, behalve de kleinste datasets, dus in de meeste gevallen is het verstandig om te beginnen met het schrijven (of typen) van je gegevens. Als u met papier en een potlood werkt, volstaat het om de waarden van uw dataset achter elkaar te schrijven, terwijl u, als u een computer gebruikt, een spreadsheetprogramma wilt gebruiken om het proces te stroomlijnen.  2 Bestel de nummers van klein naar groot. Vervolgens is het vaak een verstandig idee om de waarden van uw gegevensset zo te sorteren dat ze in stijgende volgorde staan. Hoewel dit niet strikt vereist is, maakt het het proces van het vinden van de modus gemakkelijker omdat het identieke waarden naast elkaar groepeert. Voor grote gegevenssets kan het praktisch een noodzaak zijn, omdat het sorteren van lange lijsten met waarden en het bijhouden van mentale overeenkomsten van hoe vaak elk getal in de lijst voorkomt, moeilijk is en tot fouten kan leiden.
2 Bestel de nummers van klein naar groot. Vervolgens is het vaak een verstandig idee om de waarden van uw gegevensset zo te sorteren dat ze in stijgende volgorde staan. Hoewel dit niet strikt vereist is, maakt het het proces van het vinden van de modus gemakkelijker omdat het identieke waarden naast elkaar groepeert. Voor grote gegevenssets kan het praktisch een noodzaak zijn, omdat het sorteren van lange lijsten met waarden en het bijhouden van mentale overeenkomsten van hoe vaak elk getal in de lijst voorkomt, moeilijk is en tot fouten kan leiden.  3 Tel het aantal keren dat elk nummer wordt herhaald. Tel hierna het aantal keren dat elk nummer in de set wordt weergegeven. Zoek naar de waarde die het meest voorkomt in de dataset. Voor relatief kleine gegevenssets met punten die in oplopende volgorde zijn gerangschikt, is dit meestal een kwestie van het vinden van de grootste "cluster" van identieke waarden en het tellen van het aantal keren.
3 Tel het aantal keren dat elk nummer wordt herhaald. Tel hierna het aantal keren dat elk nummer in de set wordt weergegeven. Zoek naar de waarde die het meest voorkomt in de dataset. Voor relatief kleine gegevenssets met punten die in oplopende volgorde zijn gerangschikt, is dit meestal een kwestie van het vinden van de grootste "cluster" van identieke waarden en het tellen van het aantal keren.  4 Identificeer de waarde (of waarden) die het meest voorkomen. Als u weet hoeveel keer elke waarde voorkomt in uw gegevensset, zoekt u de waarde die het grootste aantal keren voorkomt. Dit is de modus van uw dataset. Let daar op er kan meer dan één modus in een dataset zijn. Als de twee waarden gelijk zijn aan de meest voorkomende waarden in de set, kan worden gesteld dat de gegevensset dat is bimodale, terwijl als drie waarden zijn gekoppeld, de set is trimodale, enzovoort.
4 Identificeer de waarde (of waarden) die het meest voorkomen. Als u weet hoeveel keer elke waarde voorkomt in uw gegevensset, zoekt u de waarde die het grootste aantal keren voorkomt. Dit is de modus van uw dataset. Let daar op er kan meer dan één modus in een dataset zijn. Als de twee waarden gelijk zijn aan de meest voorkomende waarden in de set, kan worden gesteld dat de gegevensset dat is bimodale, terwijl als drie waarden zijn gekoppeld, de set is trimodale, enzovoort.  5 Verwar de modus van een gegevensset niet met het gemiddelde of de mediaan. Drie statistische concepten die vaak samen worden besproken, zijn middelen, medianen en modi. Omdat deze concepten allemaal hetzelfde klinkende namen hebben en omdat voor een enkele gegevensset soms een enkele waarde kan zijn meer dan een van deze dingen is het gemakkelijk om ze te verwarren. Ongeacht of de modus van de dataset ook mediaan of gemiddeld is, het is belangrijk om te begrijpen dat deze drie concepten volledig onafhankelijk van elkaar zijn. Zie hieronder:
5 Verwar de modus van een gegevensset niet met het gemiddelde of de mediaan. Drie statistische concepten die vaak samen worden besproken, zijn middelen, medianen en modi. Omdat deze concepten allemaal hetzelfde klinkende namen hebben en omdat voor een enkele gegevensset soms een enkele waarde kan zijn meer dan een van deze dingen is het gemakkelijk om ze te verwarren. Ongeacht of de modus van de dataset ook mediaan of gemiddeld is, het is belangrijk om te begrijpen dat deze drie concepten volledig onafhankelijk van elkaar zijn. Zie hieronder: 

 1 Erken dat er geen modus bestaat voor gegevenssets waarin elke waarde hetzelfde aantal keren voorkomt. Als de waarden in een bepaalde set allemaal hetzelfde aantal keren voorkomen, heeft de dataset geen modus omdat geen nummer vaker voorkomt dan andere. Gegevenssets waarin elke waarde één keer voorkomt, hebben bijvoorbeeld geen modus. Hetzelfde geldt voor datasets waarin elke waarde tweemaal, driemaal, enzovoort voorkomt.
1 Erken dat er geen modus bestaat voor gegevenssets waarin elke waarde hetzelfde aantal keren voorkomt. Als de waarden in een bepaalde set allemaal hetzelfde aantal keren voorkomen, heeft de dataset geen modus omdat geen nummer vaker voorkomt dan andere. Gegevenssets waarin elke waarde één keer voorkomt, hebben bijvoorbeeld geen modus. Hetzelfde geldt voor datasets waarin elke waarde tweemaal, driemaal, enzovoort voorkomt.  2 Erken dat modi voor niet-numerieke gegevenssets op dezelfde manier kunnen worden gevonden als voor numerieke gegevenssets. Over het algemeen zijn de meeste datasets kwantitatief - ze omgaan met gegevens in de vorm van getallen. Bepaalde gegevenssets hebben echter te maken met gegevens die niet in de vorm van getallen worden uitgedrukt. In deze gevallen kan worden gezegd dat de "modus" de enige waarde is die het meest voorkomt in de gegevensverzameling, net zoals bij numerieke gegevenssets.[1] In deze gevallen is het mogelijk om de modus te vinden terwijl het onmogelijk is om een zinvolle mediaan of gemiddelde waarde voor de gegevensset te vinden.
2 Erken dat modi voor niet-numerieke gegevenssets op dezelfde manier kunnen worden gevonden als voor numerieke gegevenssets. Over het algemeen zijn de meeste datasets kwantitatief - ze omgaan met gegevens in de vorm van getallen. Bepaalde gegevenssets hebben echter te maken met gegevens die niet in de vorm van getallen worden uitgedrukt. In deze gevallen kan worden gezegd dat de "modus" de enige waarde is die het meest voorkomt in de gegevensverzameling, net zoals bij numerieke gegevenssets.[1] In deze gevallen is het mogelijk om de modus te vinden terwijl het onmogelijk is om een zinvolle mediaan of gemiddelde waarde voor de gegevensset te vinden.  3 Erken dat voor unimodale symmetrische verdelingen de modus, het gemiddelde en de mediaan samenvallen. Zoals hierboven vermeld, is het mogelijk dat de modus, mediaan en / of gemiddelde in bepaalde gevallen overlappen. Selecteer in speciale gevallen waarin de dichtheidsfunctie van de gegevensverzameling een perfect symmetrische curve vormt met één modus (bijvoorbeeld de Gausse of "Bel-vormige" curve), de modus, het gemiddelde en de mediaan hebben allemaal dezelfde waarde. Omdat een distributiefunctie het relatieve voorkomen van gegevenspunten weergeeft, bevindt de modus zich uiteraard precies in het midden van een symmetrische verdelingskromme, omdat dit het hoogste punt in de grafiek is en overeenkomt met de meest gebruikelijke waarde. Omdat de dataset symmetrisch is, komt dit punt op de grafiek overeen met de mediaan - de middelste waarde in de gegevensset - en het gemiddelde - het gemiddelde van de gegevensverzameling.
3 Erken dat voor unimodale symmetrische verdelingen de modus, het gemiddelde en de mediaan samenvallen. Zoals hierboven vermeld, is het mogelijk dat de modus, mediaan en / of gemiddelde in bepaalde gevallen overlappen. Selecteer in speciale gevallen waarin de dichtheidsfunctie van de gegevensverzameling een perfect symmetrische curve vormt met één modus (bijvoorbeeld de Gausse of "Bel-vormige" curve), de modus, het gemiddelde en de mediaan hebben allemaal dezelfde waarde. Omdat een distributiefunctie het relatieve voorkomen van gegevenspunten weergeeft, bevindt de modus zich uiteraard precies in het midden van een symmetrische verdelingskromme, omdat dit het hoogste punt in de grafiek is en overeenkomt met de meest gebruikelijke waarde. Omdat de dataset symmetrisch is, komt dit punt op de grafiek overeen met de mediaan - de middelste waarde in de gegevensset - en het gemiddelde - het gemiddelde van de gegevensverzameling.