Lijnvermenigvuldiging wordt soms stick-vermenigvuldiging genoemd en de oorsprong is onduidelijk, met een bron waarvan wordt beweerd dat deze van de Japanners afkomstig is,[1] Chinese,[2] of Vedische culturen.[3] Het is in principe hetzelfde proces als het standaard vermenigvuldigingsalgoritme dat u op school hebt geleerd, behalve dat het op een meer visuele manier wordt weergegeven. Door gebruik te maken van de kruising van lijnen of stokjes om aan te geven waar u verschillende plaatswaarden vermenigvuldigt, kan deze methode nuttig zijn voor die studenten die meer visueel georiënteerd zijn.
Deel een van de twee:
Het probleem oplossen
-
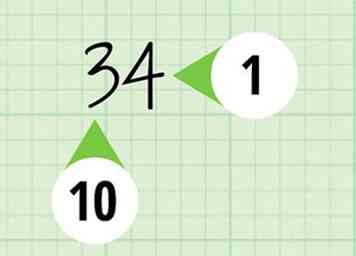 1 Bepaal de plaatswaarden van uw eerste nummer. U moet weten hoeveel plaatsen in uw nummer zijn en welk cijfer in elke plaats staat.
1 Bepaal de plaatswaarden van uw eerste nummer. U moet weten hoeveel plaatsen in uw nummer zijn en welk cijfer in elke plaats staat. - Bijvoorbeeld, als u vermenigvuldigt , je zou bepalen dat het eerste getal, 34, een 4 heeft op de plaats, en een 3 op de tiende plaats.
-
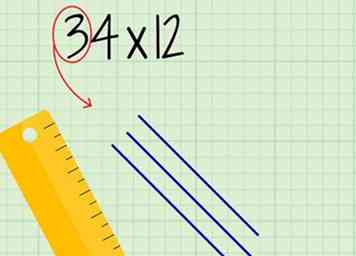 2 Trek evenwijdige lijnen om de tienste plaats van uw eerste nummer te vertegenwoordigen. Het aantal lijnen dat u tekent komt overeen met het cijfer op de tiende plaats.
2 Trek evenwijdige lijnen om de tienste plaats van uw eerste nummer te vertegenwoordigen. Het aantal lijnen dat u tekent komt overeen met het cijfer op de tiende plaats. - Teken de lijnen in een hoek van ongeveer 45 graden, schuin naar rechts.
- Als u bijvoorbeeld 34 vertegenwoordigt, tekent u 3 parallelle lijnen.
-
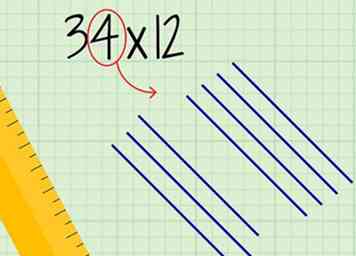 3 Trek parallelle lijnen om de plaatsen van uw eerste nummer weer te geven. Het aantal regels komt overeen met het cijfer op de plaats. Teken deze lijnen boven en rechts van de tientallen lijnen.
3 Trek parallelle lijnen om de plaatsen van uw eerste nummer weer te geven. Het aantal regels komt overeen met het cijfer op de plaats. Teken deze lijnen boven en rechts van de tientallen lijnen. - Laat wat ruimte tussen de lijnen en de tientallen lijnen, zodat je ze uit elkaar kunt houden.
- Als u bijvoorbeeld 34 vertegenwoordigt, tekent u 4 parallelle lijnen.
-
 4 Bepaal de plaatswaarden van uw tweede nummer. U moet weten hoeveel plaatsen in uw nummer zijn en welk cijfer in elke plaats staat.
4 Bepaal de plaatswaarden van uw tweede nummer. U moet weten hoeveel plaatsen in uw nummer zijn en welk cijfer in elke plaats staat. - Als je tweede getal bijvoorbeeld 12 is, zou je bepalen dat je een 2 hebt op de plaats en een 1 op de tiende plaats.
-
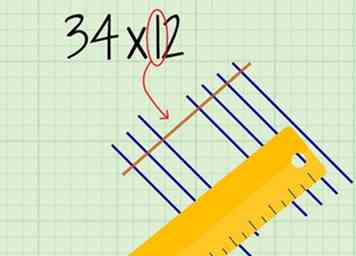 5 Trek evenwijdige lijnen om de tienden van uw tweede getal te vertegenwoordigen. Het aantal regels correspondeert met het cijfer op de tiende plaats. Teken de lijnen aan de bovenkant van het diagram. Ze moeten alle lijnen van het eerste getal overschrijden, schuin in de tegenovergestelde richting.
5 Trek evenwijdige lijnen om de tienden van uw tweede getal te vertegenwoordigen. Het aantal regels correspondeert met het cijfer op de tiende plaats. Teken de lijnen aan de bovenkant van het diagram. Ze moeten alle lijnen van het eerste getal overschrijden, schuin in de tegenovergestelde richting. - Het kan handig zijn om de lijnen van elk cijfer in een andere kleur te tekenen.
- Als u bijvoorbeeld het getal 12 vertegenwoordigt, tekent u 1 parallelle lijnkruising over de regelsets van het eerste cijfer.
-
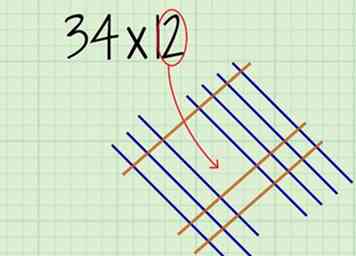 6 Teken parallelle lijnen om de plaatsen van uw tweede nummer weer te geven. Het aantal regels komt overeen met het cijfer op de plaats. Trek de lijnen onder die lijnen, zodat ze alle lijnen van het eerste getal oversteken, schuin in de tegenovergestelde richting.
6 Teken parallelle lijnen om de plaatsen van uw tweede nummer weer te geven. Het aantal regels komt overeen met het cijfer op de plaats. Trek de lijnen onder die lijnen, zodat ze alle lijnen van het eerste getal oversteken, schuin in de tegenovergestelde richting. - Laat wat ruimte tussen de lijnen en de tientallen lijnen, zodat je ze uit elkaar kunt houden.
- Als u bijvoorbeeld 12 vertegenwoordigt, tekent u 2 parallelle lijnen onder de 1 lijn die u tekende voor de tientallen.
-
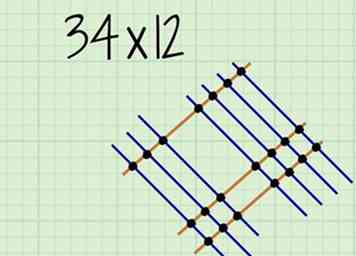 7 Teken stippen op elk punt waar de lijnen elkaar kruisen. In de lijnvermenigvuldigingsmethode, zal je deze lijnen optellen in plaats van het werkelijk vermenigvuldigen.
7 Teken stippen op elk punt waar de lijnen elkaar kruisen. In de lijnvermenigvuldigingsmethode, zal je deze lijnen optellen in plaats van het werkelijk vermenigvuldigen.
Deel twee van twee:
Het probleem oplossen
-
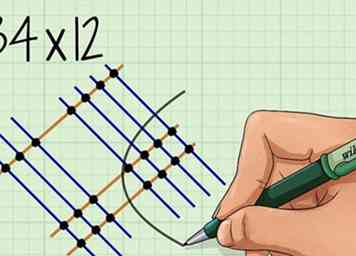 1 Omcirkel de set stippen die de plaatsen vertegenwoordigen. Dit zijn de stippen gevormd op de kruising waar de lijnen voor elk getal elkaar snijden.
1 Omcirkel de set stippen die de plaatsen vertegenwoordigen. Dit zijn de stippen gevormd op de kruising waar de lijnen voor elk getal elkaar snijden. - Denk aan: "Een één keer één is gelijk aan één."
- Bijvoorbeeld voor , je zou de gevormde punten omcirkelen waar de 4 lijnen elkaar snijden met de 2 lijnen, die in de set aan de rechterkant van het diagram staan.
-
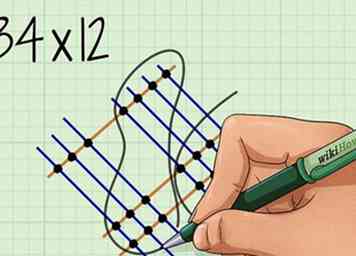 2 Omcirkel de twee sets stippen die de tientallen vertegenwoordigen. Dit zijn de punten die worden gevormd wanneer het cijfer van een van beide cijfers de tientallen van het andere getal doorkruist.
2 Omcirkel de twee sets stippen die de tientallen vertegenwoordigen. Dit zijn de punten die worden gevormd wanneer het cijfer van een van beide cijfers de tientallen van het andere getal doorkruist. - Denk aan: "Een één keer een tien is gelijk aan een tien."
- Bijvoorbeeld voor , je zou de gevormde punten omcirkelen waar de 1 lijn de 4 lijnen snijdt, en waar de 2 lijnen elkaar kruisen met de 3 lijnen, die zich in het midden van het diagram bevinden.
-
 3 Omcirkel de reeks stippen die de plaats van de honderden vertegenwoordigen. Dit zijn de stippen gevormd op de kruising waar de tientallen lijnen voor elk getal elkaar kruisen.
3 Omcirkel de reeks stippen die de plaats van de honderden vertegenwoordigen. Dit zijn de stippen gevormd op de kruising waar de tientallen lijnen voor elk getal elkaar kruisen. - Denk aan: "Een tien keer een tien is honderd."
- Bijvoorbeeld voor , je zou de gevormde punten omcirkelen waar de 3 lijnen elkaar kruisen met de 1 lijn, die zich aan de linkerkant van het diagram bevindt.
-
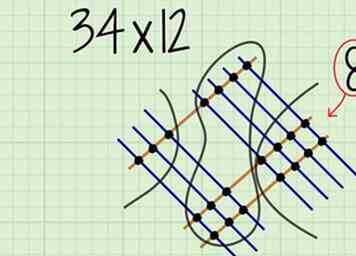 4 Tel de punten bij elkaar op. Dit zijn de stippen die je aan de rechterkant van het diagram hebt omcirkeld. Dit nummer staat op de plaats van je antwoord.
4 Tel de punten bij elkaar op. Dit zijn de stippen die je aan de rechterkant van het diagram hebt omcirkeld. Dit nummer staat op de plaats van je antwoord. - Voor , je zou 8 stippen moeten tellen. Zo zal het cijfer zijn in de plaats van je laatste antwoord.
-
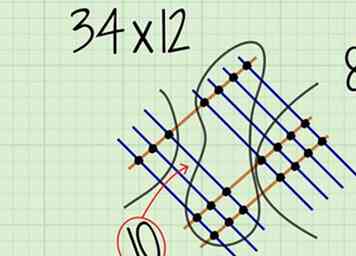 5 Tel de punten op in de tientallen. Dit zijn de twee sets stippen in het midden van het diagram. Dit nummer staat op de tiende plaats van je antwoord.
5 Tel de punten op in de tientallen. Dit zijn de twee sets stippen in het midden van het diagram. Dit nummer staat op de tiende plaats van je antwoord. - Voor , je zou 10 punten moeten tellen.
- Net zoals elke keer dat u een waarde toevoegt of vermenigvuldigt, moet u de waarde dragen zodra een cijfer op elke willekeurige plaats de waarde 10 heeft bereikt.[4] Dus als je 10 voor de tientallen meetelt, plaats je een in de tientallen plaats, en draag de 1 naar de honderdste plaats.
-
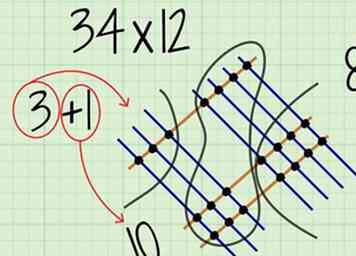 6 Tel de punten bij elkaar op de honderden plaatsen. Dit zijn de stippen die je aan de linkerkant van het diagram hebt omcirkeld. Dit nummer is de plaats van uw antwoord op honderden plaatsen.
6 Tel de punten bij elkaar op de honderden plaatsen. Dit zijn de stippen die je aan de linkerkant van het diagram hebt omcirkeld. Dit nummer is de plaats van uw antwoord op honderden plaatsen. - Voor , je zou 3 punten moeten tellen.
- Vergeet niet om een bedrag toe te voegen dat je hebt overgedragen. Voor , je droeg een 1 over van de tientallen, dus bereken . Zo wordt het cijfer op de honderdste plaats van je laatste antwoord.
-
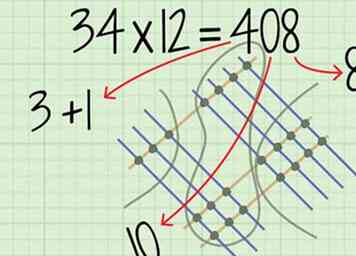 7 Bepaal uw definitieve antwoord. Stel alle cijfers samen die u hebt gevonden voor elke plaatswaarde.
7 Bepaal uw definitieve antwoord. Stel alle cijfers samen die u hebt gevonden voor elke plaatswaarde. - Bijvoorbeeld voor , u bepaalt een gaat op de plaats, a gaat in de tientallen plaats, en een gaat op de honderden plaatsen. Dus je laatste antwoord is .
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Bepaal de plaatswaarden van uw eerste nummer. U moet weten hoeveel plaatsen in uw nummer zijn en welk cijfer in elke plaats staat.
1 Bepaal de plaatswaarden van uw eerste nummer. U moet weten hoeveel plaatsen in uw nummer zijn en welk cijfer in elke plaats staat.  2 Trek evenwijdige lijnen om de tienste plaats van uw eerste nummer te vertegenwoordigen. Het aantal lijnen dat u tekent komt overeen met het cijfer op de tiende plaats.
2 Trek evenwijdige lijnen om de tienste plaats van uw eerste nummer te vertegenwoordigen. Het aantal lijnen dat u tekent komt overeen met het cijfer op de tiende plaats.  3 Trek parallelle lijnen om de plaatsen van uw eerste nummer weer te geven. Het aantal regels komt overeen met het cijfer op de plaats. Teken deze lijnen boven en rechts van de tientallen lijnen.
3 Trek parallelle lijnen om de plaatsen van uw eerste nummer weer te geven. Het aantal regels komt overeen met het cijfer op de plaats. Teken deze lijnen boven en rechts van de tientallen lijnen.  4 Bepaal de plaatswaarden van uw tweede nummer. U moet weten hoeveel plaatsen in uw nummer zijn en welk cijfer in elke plaats staat.
4 Bepaal de plaatswaarden van uw tweede nummer. U moet weten hoeveel plaatsen in uw nummer zijn en welk cijfer in elke plaats staat.  5 Trek evenwijdige lijnen om de tienden van uw tweede getal te vertegenwoordigen. Het aantal regels correspondeert met het cijfer op de tiende plaats. Teken de lijnen aan de bovenkant van het diagram. Ze moeten alle lijnen van het eerste getal overschrijden, schuin in de tegenovergestelde richting.
5 Trek evenwijdige lijnen om de tienden van uw tweede getal te vertegenwoordigen. Het aantal regels correspondeert met het cijfer op de tiende plaats. Teken de lijnen aan de bovenkant van het diagram. Ze moeten alle lijnen van het eerste getal overschrijden, schuin in de tegenovergestelde richting.  6 Teken parallelle lijnen om de plaatsen van uw tweede nummer weer te geven. Het aantal regels komt overeen met het cijfer op de plaats. Trek de lijnen onder die lijnen, zodat ze alle lijnen van het eerste getal oversteken, schuin in de tegenovergestelde richting.
6 Teken parallelle lijnen om de plaatsen van uw tweede nummer weer te geven. Het aantal regels komt overeen met het cijfer op de plaats. Trek de lijnen onder die lijnen, zodat ze alle lijnen van het eerste getal oversteken, schuin in de tegenovergestelde richting.  7 Teken stippen op elk punt waar de lijnen elkaar kruisen. In de lijnvermenigvuldigingsmethode, zal je deze lijnen optellen in plaats van het werkelijk vermenigvuldigen.
7 Teken stippen op elk punt waar de lijnen elkaar kruisen. In de lijnvermenigvuldigingsmethode, zal je deze lijnen optellen in plaats van het werkelijk vermenigvuldigen. 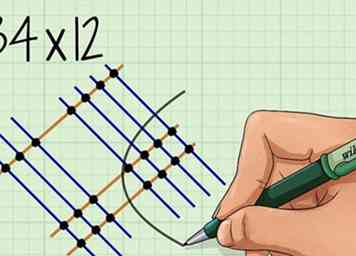 1 Omcirkel de set stippen die de plaatsen vertegenwoordigen. Dit zijn de stippen gevormd op de kruising waar de lijnen voor elk getal elkaar snijden.
1 Omcirkel de set stippen die de plaatsen vertegenwoordigen. Dit zijn de stippen gevormd op de kruising waar de lijnen voor elk getal elkaar snijden.  2 Omcirkel de twee sets stippen die de tientallen vertegenwoordigen. Dit zijn de punten die worden gevormd wanneer het cijfer van een van beide cijfers de tientallen van het andere getal doorkruist.
2 Omcirkel de twee sets stippen die de tientallen vertegenwoordigen. Dit zijn de punten die worden gevormd wanneer het cijfer van een van beide cijfers de tientallen van het andere getal doorkruist.  3 Omcirkel de reeks stippen die de plaats van de honderden vertegenwoordigen. Dit zijn de stippen gevormd op de kruising waar de tientallen lijnen voor elk getal elkaar kruisen.
3 Omcirkel de reeks stippen die de plaats van de honderden vertegenwoordigen. Dit zijn de stippen gevormd op de kruising waar de tientallen lijnen voor elk getal elkaar kruisen.  4 Tel de punten bij elkaar op. Dit zijn de stippen die je aan de rechterkant van het diagram hebt omcirkeld. Dit nummer staat op de plaats van je antwoord.
4 Tel de punten bij elkaar op. Dit zijn de stippen die je aan de rechterkant van het diagram hebt omcirkeld. Dit nummer staat op de plaats van je antwoord.  5 Tel de punten op in de tientallen. Dit zijn de twee sets stippen in het midden van het diagram. Dit nummer staat op de tiende plaats van je antwoord.
5 Tel de punten op in de tientallen. Dit zijn de twee sets stippen in het midden van het diagram. Dit nummer staat op de tiende plaats van je antwoord.  6 Tel de punten bij elkaar op de honderden plaatsen. Dit zijn de stippen die je aan de linkerkant van het diagram hebt omcirkeld. Dit nummer is de plaats van uw antwoord op honderden plaatsen.
6 Tel de punten bij elkaar op de honderden plaatsen. Dit zijn de stippen die je aan de linkerkant van het diagram hebt omcirkeld. Dit nummer is de plaats van uw antwoord op honderden plaatsen.  7 Bepaal uw definitieve antwoord. Stel alle cijfers samen die u hebt gevonden voor elke plaatswaarde.
7 Bepaal uw definitieve antwoord. Stel alle cijfers samen die u hebt gevonden voor elke plaatswaarde.