Gehele getallen zijn positieve of negatieve hele getallen zonder een decimaal of fractioneel component. Het vermenigvuldigen en delen van twee of meer gehele getallen verschilt niet veel van het vermenigvuldigen en delen van elementaire gehele getallen. Het belangrijkste verschil is dat, omdat sommige gehele getallen negatief zijn, u hun tekens moet volgen. Rekening houdend met de tekens van uw gehele getallen, kunt u doorgaan met vermenigvuldigen zoals normaal.
Stappen
Algemene informatie
-
 1 Ken uw gehele getallen. Een geheel getal is een geheel getal dat kan worden weergegeven zonder een breuk of decimaal te gebruiken. Gehele getallen kunnen positief, negatief of nul zijn. De volgende getallen zijn bijvoorbeeld gehele getallen: 1, 99, -217 en 0. Deze getallen zijn echter niet: -10,4, 6 ¾, 2,12.
1 Ken uw gehele getallen. Een geheel getal is een geheel getal dat kan worden weergegeven zonder een breuk of decimaal te gebruiken. Gehele getallen kunnen positief, negatief of nul zijn. De volgende getallen zijn bijvoorbeeld gehele getallen: 1, 99, -217 en 0. Deze getallen zijn echter niet: -10,4, 6 ¾, 2,12. - Absolute waarden kunnen gehele getallen zijn, maar ze zijn niet noodzakelijkerwijs. Een absolute waarde van elk getal is de "grootte" of "hoeveelheid" van het nummer, ongeacht het teken. Een andere manier om dit te zeggen is dat de absolute waarde van een gegeven getal de afstand van dat aantal tot nul is. De absolute waarde van een geheel getal is dus altijd een geheel getal. De absolute waarde van -12 is bijvoorbeeld 12. De absolute waarde van 3 is 3. De absolute waarde van 0 is 0.
- De absolute waarden van getallen die geen gehele getallen zijn, zullen echter nooit gehele getallen zijn. De absolute waarde van 1/11 is bijvoorbeeld 1/11 - een breuk en dus geen geheel getal.
- Absolute waarden kunnen gehele getallen zijn, maar ze zijn niet noodzakelijkerwijs. Een absolute waarde van elk getal is de "grootte" of "hoeveelheid" van het nummer, ongeacht het teken. Een andere manier om dit te zeggen is dat de absolute waarde van een gegeven getal de afstand van dat aantal tot nul is. De absolute waarde van een geheel getal is dus altijd een geheel getal. De absolute waarde van -12 is bijvoorbeeld 12. De absolute waarde van 3 is 3. De absolute waarde van 0 is 0.
- 2 Ken uw basistijdenlijsten. Het proces van het vermenigvuldigen of delen van gehele getallen, of ze nu groot of klein zijn, is veel, veel sneller en gemakkelijker als je de producten van elk paar getallen uit het hoofd leert van 1 tot 10. Deze informatie wordt meestal in school als "tijden" aangeduid tafels". Als opfriscursus hieronder is een standaard 10X10 keer tafel. De nummers aan de bovenkant en linkerkant van de tabel bevatten de getallen van 1 tot 10. Om het product van twee van deze nummers te vinden, zoekt u de cel op waar de rij en kolom van uw twee gewenste nummers elkaar kruisen:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |

Methode één van de twee:
Integers vermenigvuldigen
-
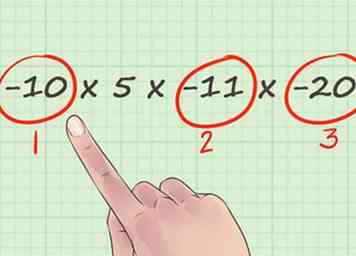 1 Tel het aantal negatieve tekens in uw vermenigvuldigingsprobleem. Een eenvoudig vermenigvuldigingsprobleem tussen twee of meer positieve getallen zal altijd resulteren in een positief antwoord. Elk negatief teken dat aan een vermenigvuldigingsprobleem is toegevoegd, schakelt het teken echter van positief naar negatief of vice versa. Om een probleem van vermenigvuldiging met gehele getallen te beginnen, telt u het aantal negatieve tekens in het probleem.
1 Tel het aantal negatieve tekens in uw vermenigvuldigingsprobleem. Een eenvoudig vermenigvuldigingsprobleem tussen twee of meer positieve getallen zal altijd resulteren in een positief antwoord. Elk negatief teken dat aan een vermenigvuldigingsprobleem is toegevoegd, schakelt het teken echter van positief naar negatief of vice versa. Om een probleem van vermenigvuldiging met gehele getallen te beginnen, telt u het aantal negatieve tekens in het probleem. - Laten we het voorbeeldprobleem -10 × 5 × -11 × -20 gebruiken. In dit probleem kunnen we duidelijk zien drie negatieve tekens. We zullen deze informatie in de volgende stap gebruiken.
-
 2 Bepaal het teken van uw antwoord op basis van het aantal negatieve signalen in het probleem. Zoals hierboven opgemerkt, zal het antwoord op een vermenigvuldigingsprobleem met alleen positieve gehele getallen positief zijn. Voor elk negatief negatief teken in uw probleem draait u het teken van uw antwoord om. Met andere woorden, als uw probleem één negatief teken heeft, is uw antwoord negatief; als het er twee heeft, zal je antwoord positief zijn, enzovoort. Een goede vuistregel is dat oneven aantal negatieve tekens geef negatieve antwoorden en zelfs aantallen negatieve tekens geef positieve antwoorden.
2 Bepaal het teken van uw antwoord op basis van het aantal negatieve signalen in het probleem. Zoals hierboven opgemerkt, zal het antwoord op een vermenigvuldigingsprobleem met alleen positieve gehele getallen positief zijn. Voor elk negatief negatief teken in uw probleem draait u het teken van uw antwoord om. Met andere woorden, als uw probleem één negatief teken heeft, is uw antwoord negatief; als het er twee heeft, zal je antwoord positief zijn, enzovoort. Een goede vuistregel is dat oneven aantal negatieve tekens geef negatieve antwoorden en zelfs aantallen negatieve tekens geef positieve antwoorden. - In ons voorbeeld hebben we drie negatieve signalen. Drie is een oneven getal, dus we weten dat ons antwoord is negatief. We kunnen een negatief teken plaatsen in de ruimte voor ons antwoord, zoals dit: -10 × 5 × -11 × -20 = -__
-
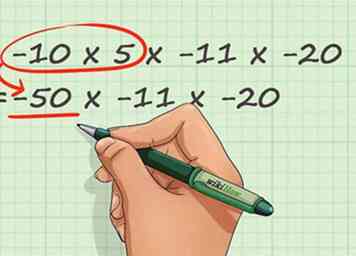 3 Vermenigvuldig getallen van 1 - 10 met behulp van elementaire tijden tabelkennis. Het product van twee getallen kleiner dan of gelijk aan 10 is gedekt in tabellen met basistijden (zie hierboven). Schrijf voor deze eenvoudige gevallen het antwoord. Onthoud dat bij problemen die alleen vermenigvuldigingstekens gebruiken, u de gehele getallen kunt verplaatsen zodat u eenvoudige getallen met elkaar kunt vermenigvuldigen.
3 Vermenigvuldig getallen van 1 - 10 met behulp van elementaire tijden tabelkennis. Het product van twee getallen kleiner dan of gelijk aan 10 is gedekt in tabellen met basistijden (zie hierboven). Schrijf voor deze eenvoudige gevallen het antwoord. Onthoud dat bij problemen die alleen vermenigvuldigingstekens gebruiken, u de gehele getallen kunt verplaatsen zodat u eenvoudige getallen met elkaar kunt vermenigvuldigen. - In ons voorbeeld is 10 × 5 opgenomen in de tabel met basistijden. We hoeven geen rekening te houden met het negatieve teken van de tien omdat we het teken van ons antwoord al hebben gevonden. 10 × 5 = 50. We kunnen dit als volgt in ons probleem invoegen: (50) × -11 × -20 = -__
- Als u problemen ondervindt bij het visualiseren van eenvoudige vermenigvuldigingsproblemen, moet u ze beschouwen in termen van toevoegingsproblemen. 5 × 10 is bijvoorbeeld als "vijf, tien keer". Met andere woorden, 5 × 10 = 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5.
- In ons voorbeeld is 10 × 5 opgenomen in de tabel met basistijden. We hoeven geen rekening te houden met het negatieve teken van de tien omdat we het teken van ons antwoord al hebben gevonden. 10 × 5 = 50. We kunnen dit als volgt in ons probleem invoegen: (50) × -11 × -20 = -__
-
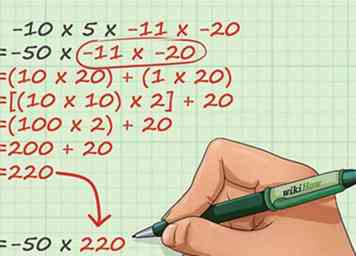 4 Breid indien nodig grotere aantallen uit in beheersbare brokken. Als uw vermenigvuldigingsprobleem bestaat uit getallen groter dan tien, hoeft u niet per se lange vermenigvuldiging te gebruiken. Kijk eerst of je een of meer van je nummers kunt opsplitsen in kleinere, meer bruikbare stukjes. Omdat, met elementaire tijden tafelkennis, je eenvoudige vermenigvuldigingsproblemen vrijwel onmiddellijk kunt oplossen, is het breken van een moeilijk probleem in een aantal van deze eenvoudige problemen meestal eenvoudiger dan het oplossen van het enkele lastige probleem.
4 Breid indien nodig grotere aantallen uit in beheersbare brokken. Als uw vermenigvuldigingsprobleem bestaat uit getallen groter dan tien, hoeft u niet per se lange vermenigvuldiging te gebruiken. Kijk eerst of je een of meer van je nummers kunt opsplitsen in kleinere, meer bruikbare stukjes. Omdat, met elementaire tijden tafelkennis, je eenvoudige vermenigvuldigingsproblemen vrijwel onmiddellijk kunt oplossen, is het breken van een moeilijk probleem in een aantal van deze eenvoudige problemen meestal eenvoudiger dan het oplossen van het enkele lastige probleem. - Laten we naar de tweede helft van ons voorbeeldprobleem kijken, -11 × -20. We kunnen de tekens weglaten omdat we het teken van ons antwoord al hebben gevonden. 11 × 20 ziet er intimiderend uit, maar als we het probleem herschrijven als 10 × 20 + 1 × 20, is het plotseling veel beter hanteerbaar. 10 × 20 is slechts 2 keer 10 × 10 of 200. 1 × 20 is slechts 20. Bij het optellen van onze antwoorden krijgen we 200 + 20 = 220. We kunnen dit als volgt opnieuw invoegen in ons probleem: (50) × (220) = -__
-
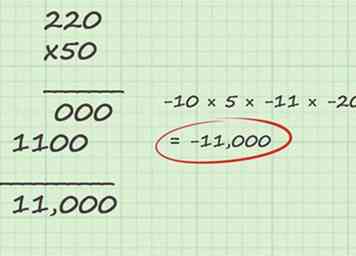 5 Gebruik voor moeilijke cijfers lange vermenigvuldigingen. Als uw vermenigvuldigingsprobleem twee of meer getallen groter dan 10 bevat en u het antwoord niet kunt vinden door uw probleem te verdelen in bruikbare brokken, kunt u dit nog steeds oplossen via een lange vermenigvuldiging.Bij lange vermenigvuldiging lijn je je antwoorden net zoals bij een optelprobleem en vermenigvuldig elk cijfer in het onderste getal met elk cijfer in het bovenste cijfer. Als het onderste getal uit meer dan één cijfer bestaat, moet u cijfers in de tientallen, honderden, enzovoort registreren in uw account door nullen toe te voegen aan de rechterkant van uw gedeeltelijke antwoord. Tot slot, om uw laatste antwoord te krijgen, telt u alle gedeeltelijke antwoorden bij elkaar op.
5 Gebruik voor moeilijke cijfers lange vermenigvuldigingen. Als uw vermenigvuldigingsprobleem twee of meer getallen groter dan 10 bevat en u het antwoord niet kunt vinden door uw probleem te verdelen in bruikbare brokken, kunt u dit nog steeds oplossen via een lange vermenigvuldiging.Bij lange vermenigvuldiging lijn je je antwoorden net zoals bij een optelprobleem en vermenigvuldig elk cijfer in het onderste getal met elk cijfer in het bovenste cijfer. Als het onderste getal uit meer dan één cijfer bestaat, moet u cijfers in de tientallen, honderden, enzovoort registreren in uw account door nullen toe te voegen aan de rechterkant van uw gedeeltelijke antwoord. Tot slot, om uw laatste antwoord te krijgen, telt u alle gedeeltelijke antwoorden bij elkaar op. - Laten we teruggaan naar ons voorbeeldprobleem. Nu moeten we 50 vermenigvuldigen met 220. Dit zal moeilijk zijn om in te breken in gemakkelijkere stukjes, dus laten we lange vermenigvuldiging gebruiken. Lange vermenigvuldigingsproblemen zijn gemakkelijker te volgen als het kleinere getal onderaan staat, dus laten we ons probleem beschrijven met 220 bovenop en 50 met onderaan.
- Vermenigvuldig eerst het cijfer op de plaats van het onderste cijfer met elk cijfer van het bovenste cijfer. Aangezien 50 onderaan staat, is 0 het cijfer op de plaats. 0 × 0 is 0, 0 × 2 is 0 en 0 × 2 is nul. Met andere woorden, 0 × 220 is nul. Schrijf dit hieronder uw lange vermenigvuldigingsprobleem op die plaats. Dit is ons eerste gedeeltelijke antwoord.
- Vervolgens vermenigvuldigen we het cijfer tienden van ons onderste getal met elk cijfer van het hoogste cijfer. 5 is het cijfer op de tiende plaats van 50. Aangezien deze 5 in de tientallen plaats is, in plaats van de plaatsen, schrijven we een nul onder ons eerste gedeeltelijke antwoord in de plaats voordat we verder gaan. Vervolgens vermenigvuldigen we ons. 5 × 0 is 0. 5 × 2 is 10, dus schrijf 0 en voeg er een toe aan het product van 5 en het volgende cijfer. 5 × 2 is 10. Normaal gesproken zouden we 0 schrijven en de 1 dragen, maar in dit geval voegen we ook de 1 van het vorige probleem toe, en geven we 11. Noteer "1". Als we de 1 vanaf de tiende plaats van 11 dragen, zien we dat we geen cijfers meer hebben, dus we schrijven het tot nu toe links van ons gedeeltelijke antwoord. Door dit alles op te nemen, blijven we achter met 11.000.
- Vervolgens voegen we gewoon toe. 0 + 11.000 is 11.000. Omdat we weten dat het antwoord op ons oorspronkelijke probleem negatief is, kunnen we gerust zeggen dat -10 × 5 × -11 × -20 = -11,000.
- Laten we teruggaan naar ons voorbeeldprobleem. Nu moeten we 50 vermenigvuldigen met 220. Dit zal moeilijk zijn om in te breken in gemakkelijkere stukjes, dus laten we lange vermenigvuldiging gebruiken. Lange vermenigvuldigingsproblemen zijn gemakkelijker te volgen als het kleinere getal onderaan staat, dus laten we ons probleem beschrijven met 220 bovenop en 50 met onderaan.
Methode twee van twee:
Integers verdelen
-
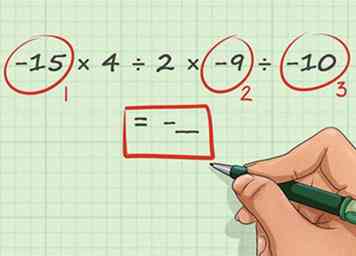 1 Bepaal als eerder het teken van uw antwoord op basis van het aantal negatieve signalen in het probleem. Een divisie introduceren in een wiskundeprobleem verandert niets aan de regels met betrekking tot negatieve signalen. Als er een oneven aantal negatieve tekens is, is het antwoord negatief, terwijl als er een even aantal negatieve tekens (of helemaal geen) is, het antwoord positief zal zijn.
1 Bepaal als eerder het teken van uw antwoord op basis van het aantal negatieve signalen in het probleem. Een divisie introduceren in een wiskundeprobleem verandert niets aan de regels met betrekking tot negatieve signalen. Als er een oneven aantal negatieve tekens is, is het antwoord negatief, terwijl als er een even aantal negatieve tekens (of helemaal geen) is, het antwoord positief zal zijn. - Laten we een voorbeeldprobleem gebruiken met zowel vermenigvuldiging als deling. In het probleem -15 × 4 ÷ 2 × -9 ÷ -10 zijn er drie negatieve tekens, dus het antwoord zal zijn negatief. Net als eerder kunnen we een negatief teken plaatsen in de ruimte voor ons antwoord, zoals dit: -15 × 4 ÷ 2 × -9 ÷ -10 = -__
-
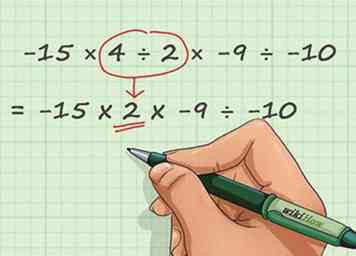 2 Maak eenvoudige onderverdelingen met behulp van uw vermenigvuldigingskennis. Een verdeling kan worden gezien als een achterwaartse vermenigvuldiging. Wanneer je het ene getal door het andere deelt, vraag je op een rotonde: "hoe vaak past het tweede getal in het eerste nummer?" of, met andere woorden, "wat heb ik nodig om het tweede getal te vermenigvuldigen met de eerste?" Raadpleeg de standaard tabel van 10 x 10 keer als referentie - als u wordt gevraagd om een van de twee te delen antwoorden in de tijdenlijst door om het even welk aantal n van 1 - 10, je weet dat het antwoord alleen het andere nummer van 1 - 10 is dat je nodig hebt om te vermenigvuldigen n het begrijpen.
2 Maak eenvoudige onderverdelingen met behulp van uw vermenigvuldigingskennis. Een verdeling kan worden gezien als een achterwaartse vermenigvuldiging. Wanneer je het ene getal door het andere deelt, vraag je op een rotonde: "hoe vaak past het tweede getal in het eerste nummer?" of, met andere woorden, "wat heb ik nodig om het tweede getal te vermenigvuldigen met de eerste?" Raadpleeg de standaard tabel van 10 x 10 keer als referentie - als u wordt gevraagd om een van de twee te delen antwoorden in de tijdenlijst door om het even welk aantal n van 1 - 10, je weet dat het antwoord alleen het andere nummer van 1 - 10 is dat je nodig hebt om te vermenigvuldigen n het begrijpen. - Laten we naar ons voorbeeldprobleem kijken. In -15 × 4 ÷ 2 × -9 ÷ -10 zien we 4 ÷ 2. 4 is een antwoord in de maaltafel - zowel 4 × 1 als 2 × 2 geven 4 als antwoord. Omdat we gevraagd worden om 4 te delen door 2, weten we dat we in principe het probleem oplossen 2 × __ = 4. In de lege ruimte zouden we natuurlijk 2 schrijven, dus 4 ÷ 2 = 2. Laten we ons probleem herschrijven als -15 × (2) × -9 ÷ -10.
-
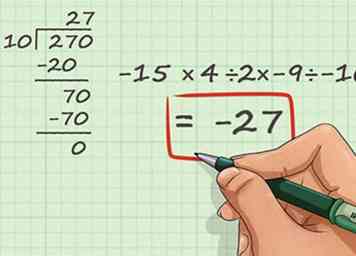 3 Gebruik long division indien nodig. Net als bij vermenigvuldiging, als je een afdelingsprobleem tegenkomt dat te moeilijk is om mentaal of met een tijdstabel uit te werken, heb je de mogelijkheid om een langetermijnaanpak op te lossen. In een probleem met de lange divisie, schrijf je je twee nummers in een speciale zijdelingse L-vormige haak, deel je vervolgens cijfer voor cijfer, verander je gedeeltelijke antwoorden naar rechts als je gaat om rekening te houden met de afnemende waarde van de cijfers die je bent delen - honderden, dan tientallen, dan degenen, enzovoort.
3 Gebruik long division indien nodig. Net als bij vermenigvuldiging, als je een afdelingsprobleem tegenkomt dat te moeilijk is om mentaal of met een tijdstabel uit te werken, heb je de mogelijkheid om een langetermijnaanpak op te lossen. In een probleem met de lange divisie, schrijf je je twee nummers in een speciale zijdelingse L-vormige haak, deel je vervolgens cijfer voor cijfer, verander je gedeeltelijke antwoorden naar rechts als je gaat om rekening te houden met de afnemende waarde van de cijfers die je bent delen - honderden, dan tientallen, dan degenen, enzovoort. - Laten we de tweedeling gebruiken in ons voorbeeldprobleem. We kunnen -15 × (2) × -9 ÷ -10 tot 270 ÷ -10 vereenvoudigen. We zullen de tekens zoals gewoonlijk negeren omdat we het teken van ons definitieve antwoord kennen. Schrijf 10 links van de L-vormige beugel en schrijf 270 eronder.
- We beginnen met het eerste cijfer van het nummer onder de haakjes te delen door het cijfer aan de zijkant. Het eerste cijfer is 2 en ons nummer aan de zijkant is 10. Aangezien 10 niet in twee past, gebruiken we in plaats daarvan de eerste twee cijfers. 10 doet passen in 27 - hij past er twee keer in. Schrijf "2" boven de 7 onder de beugel. 2 is het eerste cijfer in uw antwoord.
- Vervolgens vermenigvuldigt u het aantal links van de haakjes met het cijfer dat u zojuist hebt gevonden. 2 × 10 is 20. Schrijf dit onder de eerste twee cijfers van het nummer onder de haak - in dit geval 2 en 7.
- Trek de getallen af die u zojuist hebt geschreven. 27 minus 20 is 7. Schrijf dit onderaan je groeiprobleem.
- Laat het volgende cijfer van het nummer onder de haak vallen. Dit volgende cijfer van 270 is 0. Zet dit naast de 7 neer om 70 te maken.
- Deel je nieuwe nummer. Verdeel vervolgens 10 in 70. 10 past precies 7 keer in 70, dus schrijf aan de bovenkant naast de 2. Dit is het tweede cijfer van je antwoord. Je laatste antwoord is 27.
- Merk op dat, in het geval dat 10 niet Gelijkmatig verdelen in ons definitieve aantal, moeten we rekening houden met het bedrag van 10 dat overblijft - de rest. Bijvoorbeeld, als onze laatste daad was te verdelen 71in plaats van 70 op 10, zouden we opmerken dat 10 niet precies in 71 past. Het past 7 keer, maar er is er nog 1 over. Met andere woorden, we kunnen zeven 10en en een extra 1 in 71 passen. We zouden ons antwoord dan als volgt schrijven "27 rest 1" of "27 r1".
- Laten we de tweedeling gebruiken in ons voorbeeldprobleem. We kunnen -15 × (2) × -9 ÷ -10 tot 270 ÷ -10 vereenvoudigen. We zullen de tekens zoals gewoonlijk negeren omdat we het teken van ons definitieve antwoord kennen. Schrijf 10 links van de L-vormige beugel en schrijf 270 eronder.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Ken uw gehele getallen. Een geheel getal is een geheel getal dat kan worden weergegeven zonder een breuk of decimaal te gebruiken. Gehele getallen kunnen positief, negatief of nul zijn. De volgende getallen zijn bijvoorbeeld gehele getallen: 1, 99, -217 en 0. Deze getallen zijn echter niet: -10,4, 6 ¾, 2,12.
1 Ken uw gehele getallen. Een geheel getal is een geheel getal dat kan worden weergegeven zonder een breuk of decimaal te gebruiken. Gehele getallen kunnen positief, negatief of nul zijn. De volgende getallen zijn bijvoorbeeld gehele getallen: 1, 99, -217 en 0. Deze getallen zijn echter niet: -10,4, 6 ¾, 2,12. 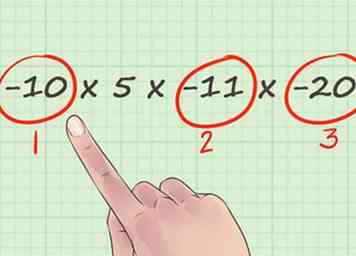 1 Tel het aantal negatieve tekens in uw vermenigvuldigingsprobleem. Een eenvoudig vermenigvuldigingsprobleem tussen twee of meer positieve getallen zal altijd resulteren in een positief antwoord. Elk negatief teken dat aan een vermenigvuldigingsprobleem is toegevoegd, schakelt het teken echter van positief naar negatief of vice versa. Om een probleem van vermenigvuldiging met gehele getallen te beginnen, telt u het aantal negatieve tekens in het probleem.
1 Tel het aantal negatieve tekens in uw vermenigvuldigingsprobleem. Een eenvoudig vermenigvuldigingsprobleem tussen twee of meer positieve getallen zal altijd resulteren in een positief antwoord. Elk negatief teken dat aan een vermenigvuldigingsprobleem is toegevoegd, schakelt het teken echter van positief naar negatief of vice versa. Om een probleem van vermenigvuldiging met gehele getallen te beginnen, telt u het aantal negatieve tekens in het probleem.  2 Bepaal het teken van uw antwoord op basis van het aantal negatieve signalen in het probleem. Zoals hierboven opgemerkt, zal het antwoord op een vermenigvuldigingsprobleem met alleen positieve gehele getallen positief zijn. Voor elk negatief negatief teken in uw probleem draait u het teken van uw antwoord om. Met andere woorden, als uw probleem één negatief teken heeft, is uw antwoord negatief; als het er twee heeft, zal je antwoord positief zijn, enzovoort. Een goede vuistregel is dat oneven aantal negatieve tekens geef negatieve antwoorden en zelfs aantallen negatieve tekens geef positieve antwoorden.
2 Bepaal het teken van uw antwoord op basis van het aantal negatieve signalen in het probleem. Zoals hierboven opgemerkt, zal het antwoord op een vermenigvuldigingsprobleem met alleen positieve gehele getallen positief zijn. Voor elk negatief negatief teken in uw probleem draait u het teken van uw antwoord om. Met andere woorden, als uw probleem één negatief teken heeft, is uw antwoord negatief; als het er twee heeft, zal je antwoord positief zijn, enzovoort. Een goede vuistregel is dat oneven aantal negatieve tekens geef negatieve antwoorden en zelfs aantallen negatieve tekens geef positieve antwoorden. 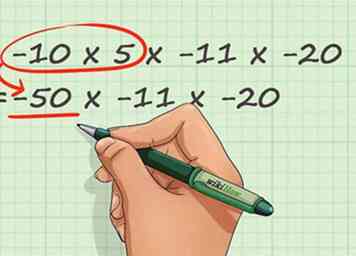 3 Vermenigvuldig getallen van 1 - 10 met behulp van elementaire tijden tabelkennis. Het product van twee getallen kleiner dan of gelijk aan 10 is gedekt in tabellen met basistijden (zie hierboven). Schrijf voor deze eenvoudige gevallen het antwoord. Onthoud dat bij problemen die alleen vermenigvuldigingstekens gebruiken, u de gehele getallen kunt verplaatsen zodat u eenvoudige getallen met elkaar kunt vermenigvuldigen.
3 Vermenigvuldig getallen van 1 - 10 met behulp van elementaire tijden tabelkennis. Het product van twee getallen kleiner dan of gelijk aan 10 is gedekt in tabellen met basistijden (zie hierboven). Schrijf voor deze eenvoudige gevallen het antwoord. Onthoud dat bij problemen die alleen vermenigvuldigingstekens gebruiken, u de gehele getallen kunt verplaatsen zodat u eenvoudige getallen met elkaar kunt vermenigvuldigen. 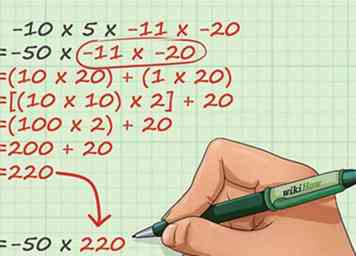 4 Breid indien nodig grotere aantallen uit in beheersbare brokken. Als uw vermenigvuldigingsprobleem bestaat uit getallen groter dan tien, hoeft u niet per se lange vermenigvuldiging te gebruiken. Kijk eerst of je een of meer van je nummers kunt opsplitsen in kleinere, meer bruikbare stukjes. Omdat, met elementaire tijden tafelkennis, je eenvoudige vermenigvuldigingsproblemen vrijwel onmiddellijk kunt oplossen, is het breken van een moeilijk probleem in een aantal van deze eenvoudige problemen meestal eenvoudiger dan het oplossen van het enkele lastige probleem.
4 Breid indien nodig grotere aantallen uit in beheersbare brokken. Als uw vermenigvuldigingsprobleem bestaat uit getallen groter dan tien, hoeft u niet per se lange vermenigvuldiging te gebruiken. Kijk eerst of je een of meer van je nummers kunt opsplitsen in kleinere, meer bruikbare stukjes. Omdat, met elementaire tijden tafelkennis, je eenvoudige vermenigvuldigingsproblemen vrijwel onmiddellijk kunt oplossen, is het breken van een moeilijk probleem in een aantal van deze eenvoudige problemen meestal eenvoudiger dan het oplossen van het enkele lastige probleem. 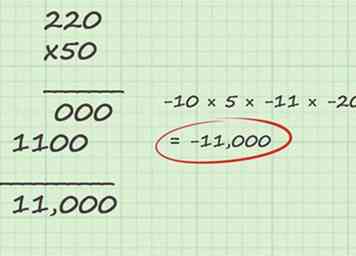 5 Gebruik voor moeilijke cijfers lange vermenigvuldigingen. Als uw vermenigvuldigingsprobleem twee of meer getallen groter dan 10 bevat en u het antwoord niet kunt vinden door uw probleem te verdelen in bruikbare brokken, kunt u dit nog steeds oplossen via een lange vermenigvuldiging.Bij lange vermenigvuldiging lijn je je antwoorden net zoals bij een optelprobleem en vermenigvuldig elk cijfer in het onderste getal met elk cijfer in het bovenste cijfer. Als het onderste getal uit meer dan één cijfer bestaat, moet u cijfers in de tientallen, honderden, enzovoort registreren in uw account door nullen toe te voegen aan de rechterkant van uw gedeeltelijke antwoord. Tot slot, om uw laatste antwoord te krijgen, telt u alle gedeeltelijke antwoorden bij elkaar op.
5 Gebruik voor moeilijke cijfers lange vermenigvuldigingen. Als uw vermenigvuldigingsprobleem twee of meer getallen groter dan 10 bevat en u het antwoord niet kunt vinden door uw probleem te verdelen in bruikbare brokken, kunt u dit nog steeds oplossen via een lange vermenigvuldiging.Bij lange vermenigvuldiging lijn je je antwoorden net zoals bij een optelprobleem en vermenigvuldig elk cijfer in het onderste getal met elk cijfer in het bovenste cijfer. Als het onderste getal uit meer dan één cijfer bestaat, moet u cijfers in de tientallen, honderden, enzovoort registreren in uw account door nullen toe te voegen aan de rechterkant van uw gedeeltelijke antwoord. Tot slot, om uw laatste antwoord te krijgen, telt u alle gedeeltelijke antwoorden bij elkaar op. 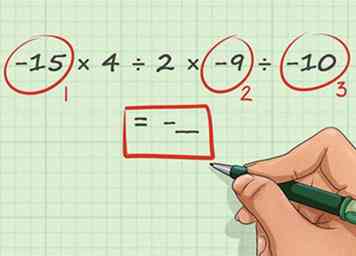 1 Bepaal als eerder het teken van uw antwoord op basis van het aantal negatieve signalen in het probleem. Een divisie introduceren in een wiskundeprobleem verandert niets aan de regels met betrekking tot negatieve signalen. Als er een oneven aantal negatieve tekens is, is het antwoord negatief, terwijl als er een even aantal negatieve tekens (of helemaal geen) is, het antwoord positief zal zijn.
1 Bepaal als eerder het teken van uw antwoord op basis van het aantal negatieve signalen in het probleem. Een divisie introduceren in een wiskundeprobleem verandert niets aan de regels met betrekking tot negatieve signalen. Als er een oneven aantal negatieve tekens is, is het antwoord negatief, terwijl als er een even aantal negatieve tekens (of helemaal geen) is, het antwoord positief zal zijn. 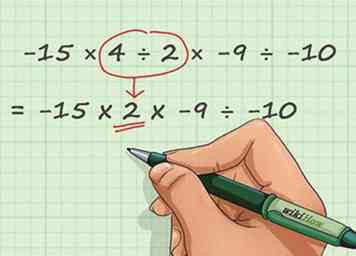 2 Maak eenvoudige onderverdelingen met behulp van uw vermenigvuldigingskennis. Een verdeling kan worden gezien als een achterwaartse vermenigvuldiging. Wanneer je het ene getal door het andere deelt, vraag je op een rotonde: "hoe vaak past het tweede getal in het eerste nummer?" of, met andere woorden, "wat heb ik nodig om het tweede getal te vermenigvuldigen met de eerste?" Raadpleeg de standaard tabel van 10 x 10 keer als referentie - als u wordt gevraagd om een van de twee te delen antwoorden in de tijdenlijst door om het even welk aantal n van 1 - 10, je weet dat het antwoord alleen het andere nummer van 1 - 10 is dat je nodig hebt om te vermenigvuldigen n het begrijpen.
2 Maak eenvoudige onderverdelingen met behulp van uw vermenigvuldigingskennis. Een verdeling kan worden gezien als een achterwaartse vermenigvuldiging. Wanneer je het ene getal door het andere deelt, vraag je op een rotonde: "hoe vaak past het tweede getal in het eerste nummer?" of, met andere woorden, "wat heb ik nodig om het tweede getal te vermenigvuldigen met de eerste?" Raadpleeg de standaard tabel van 10 x 10 keer als referentie - als u wordt gevraagd om een van de twee te delen antwoorden in de tijdenlijst door om het even welk aantal n van 1 - 10, je weet dat het antwoord alleen het andere nummer van 1 - 10 is dat je nodig hebt om te vermenigvuldigen n het begrijpen. 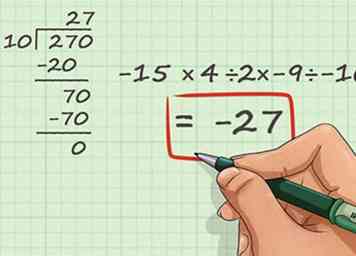 3 Gebruik long division indien nodig. Net als bij vermenigvuldiging, als je een afdelingsprobleem tegenkomt dat te moeilijk is om mentaal of met een tijdstabel uit te werken, heb je de mogelijkheid om een langetermijnaanpak op te lossen. In een probleem met de lange divisie, schrijf je je twee nummers in een speciale zijdelingse L-vormige haak, deel je vervolgens cijfer voor cijfer, verander je gedeeltelijke antwoorden naar rechts als je gaat om rekening te houden met de afnemende waarde van de cijfers die je bent delen - honderden, dan tientallen, dan degenen, enzovoort.
3 Gebruik long division indien nodig. Net als bij vermenigvuldiging, als je een afdelingsprobleem tegenkomt dat te moeilijk is om mentaal of met een tijdstabel uit te werken, heb je de mogelijkheid om een langetermijnaanpak op te lossen. In een probleem met de lange divisie, schrijf je je twee nummers in een speciale zijdelingse L-vormige haak, deel je vervolgens cijfer voor cijfer, verander je gedeeltelijke antwoorden naar rechts als je gaat om rekening te houden met de afnemende waarde van de cijfers die je bent delen - honderden, dan tientallen, dan degenen, enzovoort.