De grootste gemene deler (GCD) van twee hele getallen, ook wel de grootste gemeenschappelijke factor (GCF) en de hoogste gemeenschappelijke factor (HCF) genoemd, is het grootste gehele getal dat een deler (factor) van beide is. Het grootste getal dat in zowel 20 als 16 wordt gedeeld, is bijvoorbeeld 4. (Zowel 16 als 20 hebben grotere factoren, maar niet groter gemeenschappelijk factoren - bijvoorbeeld 8 is een factor 16, maar het is geen factor 20.) Op de basisschool wordt aan de meeste mensen een "guess-and-check" -methode voor het vinden van de GCD geleerd. In plaats daarvan is er een eenvoudige en systematische manier om dit te doen, wat altijd leidt tot het juiste antwoord. De methode wordt "Euclides algoritme" genoemd. Als u wilt weten hoe u de grootste gemene deler van twee gehele getallen kunt vinden, gaat u naar stap 1 om aan de slag te gaan.
Methode één van de twee:
Het Divisor-algoritme gebruiken
-
 1 Laat eventuele negatieve signalen vallen.
1 Laat eventuele negatieve signalen vallen. -
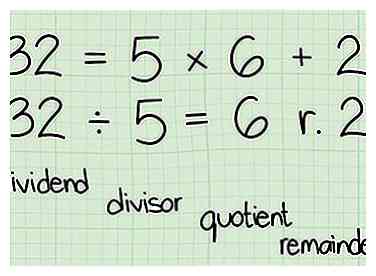 2 Ken je vocabulaire: wanneer je 32 bij 5 deelt,
2 Ken je vocabulaire: wanneer je 32 bij 5 deelt, -
- 32 is het dividend
- 5 is de deler
- 6 is het quotiënt
- 2 is de rest (of modulo).
-
-
 3 Identificeer de grootste van de twee nummers. Dat is het dividend, en hoe kleiner de deler.
3 Identificeer de grootste van de twee nummers. Dat is het dividend, en hoe kleiner de deler. -
 4 Schrijf dit algoritme op: (dividend) = (deler) * (quotiënt) + (rest)
4 Schrijf dit algoritme op: (dividend) = (deler) * (quotiënt) + (rest) -
 5 Zet het grotere aantal op de plaats voor dividend, en het kleinere aantal als de deler.
5 Zet het grotere aantal op de plaats voor dividend, en het kleinere aantal als de deler. -
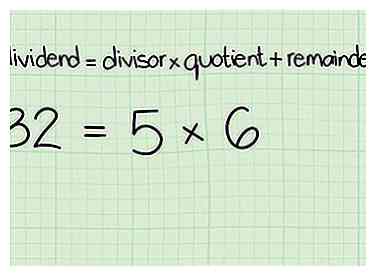 6 Bepaal hoe vaak het kleinere getal zich zal splitsen in het grotere aantal en laat dit in het algoritme vallen als het quotiënt.
6 Bepaal hoe vaak het kleinere getal zich zal splitsen in het grotere aantal en laat dit in het algoritme vallen als het quotiënt. -
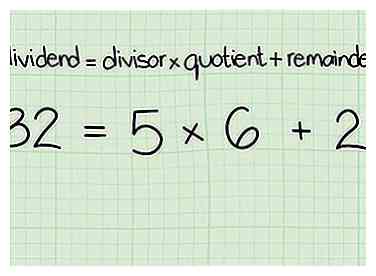 7 Bereken de rest en vervang deze op de juiste plaats in het algoritme.
7 Bereken de rest en vervang deze op de juiste plaats in het algoritme. -
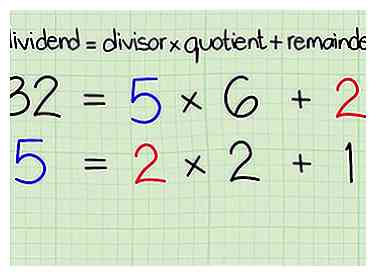 8 Schrijf het algoritme opnieuw uit, maar gebruik deze keer de oude deler als het nieuwe dividend en B) gebruik de rest als de nieuwe deler.
8 Schrijf het algoritme opnieuw uit, maar gebruik deze keer de oude deler als het nieuwe dividend en B) gebruik de rest als de nieuwe deler. -
 9 Herhaal de vorige stap totdat de rest nul is.
9 Herhaal de vorige stap totdat de rest nul is. -
 10 De laatste deler is de grootste gemene deler.
10 De laatste deler is de grootste gemene deler. -
 11 Hier is een voorbeeld, waarin we de GCD van 108 en 30 proberen te vinden:
11 Hier is een voorbeeld, waarin we de GCD van 108 en 30 proberen te vinden: -
 12 Let op hoe de 30 en de 18 in de eerste regel van positie wisselen om de tweede regel te maken. Vervolgens verschuiven de 18 en 12 om de derde lijn te maken, en de 12 en 6 shift om de vierde lijn te creëren. De 3, 1, 1 en 2 die het vermenigvuldigingssymbool volgen, verschijnen niet opnieuw. Ze geven aan hoe vaak de deler in het dividend past, dus ze zijn uniek voor elke regel.
12 Let op hoe de 30 en de 18 in de eerste regel van positie wisselen om de tweede regel te maken. Vervolgens verschuiven de 18 en 12 om de derde lijn te maken, en de 12 en 6 shift om de vierde lijn te creëren. De 3, 1, 1 en 2 die het vermenigvuldigingssymbool volgen, verschijnen niet opnieuw. Ze geven aan hoe vaak de deler in het dividend past, dus ze zijn uniek voor elke regel.
Methode twee van twee:
Prime Factors gebruiken
-
 1 Laat eventuele negatieve signalen vallen.
1 Laat eventuele negatieve signalen vallen. -
 2 Zoek de priemfactorisatie van de getallen en noteer ze zoals getoond.
2 Zoek de priemfactorisatie van de getallen en noteer ze zoals getoond. - Gebruik 24 en 18 als voorbeeldnummers:
- 24 - 2 x 2 x 2 x 3
- 18 - 2 x 3 x 3
- Gebruik 50 en 35 als voorbeeldnummers:
- 50 - 2 x 5 x 5
- 35 - 5 x 7
- Gebruik 24 en 18 als voorbeeldnummers:
-
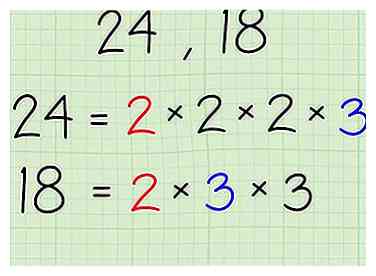 3 Identificeer alle gangbare priemgetallen.
3 Identificeer alle gangbare priemgetallen. - Gebruik 24 en 18 als voorbeeldnummers:
- 24- 2 x 2 x 2 x 3
- 18- 2 X 3 x 3
- Gebruik 50 en 35 als voorbeeldnummers:
- 50 - 2 x 5 x 5
- 35- 5 x 7
- Gebruik 24 en 18 als voorbeeldnummers:
-
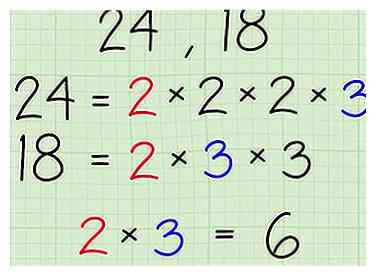 4 Vermenigvuldig de gemeenschappelijke factoren samen.
4 Vermenigvuldig de gemeenschappelijke factoren samen. - In het geval van 24 en 18, vermenigvuldig 2 en 3 samen te krijgen 6. Zes is de grootste gemene deler van 24 en 18.
- In het geval van 50 en 35 is er niets om te vermenigvuldigen. 5 is de enige gemeenschappelijke factor, en daarom de grootste.
-
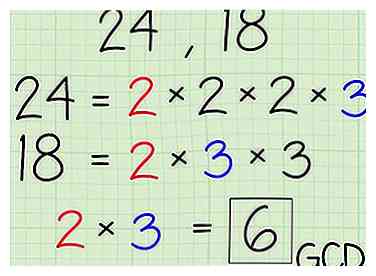 5 Afgewerkt.
5 Afgewerkt.
 Minotauromaquia
Minotauromaquia
 1 Laat eventuele negatieve signalen vallen.
1 Laat eventuele negatieve signalen vallen. 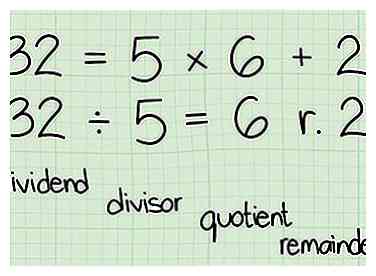 2 Ken je vocabulaire: wanneer je 32 bij 5 deelt,
2 Ken je vocabulaire: wanneer je 32 bij 5 deelt,  3 Identificeer de grootste van de twee nummers. Dat is het dividend, en hoe kleiner de deler.
3 Identificeer de grootste van de twee nummers. Dat is het dividend, en hoe kleiner de deler.  4 Schrijf dit algoritme op: (dividend) = (deler) * (quotiënt) + (rest)
4 Schrijf dit algoritme op: (dividend) = (deler) * (quotiënt) + (rest)  5 Zet het grotere aantal op de plaats voor dividend, en het kleinere aantal als de deler.
5 Zet het grotere aantal op de plaats voor dividend, en het kleinere aantal als de deler. 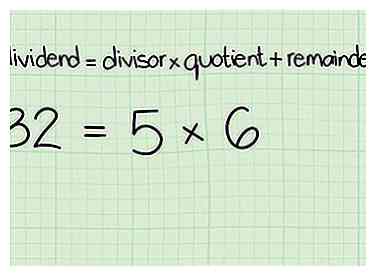 6 Bepaal hoe vaak het kleinere getal zich zal splitsen in het grotere aantal en laat dit in het algoritme vallen als het quotiënt.
6 Bepaal hoe vaak het kleinere getal zich zal splitsen in het grotere aantal en laat dit in het algoritme vallen als het quotiënt. 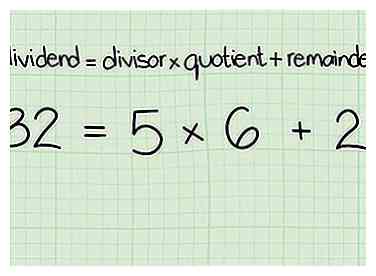 7 Bereken de rest en vervang deze op de juiste plaats in het algoritme.
7 Bereken de rest en vervang deze op de juiste plaats in het algoritme. 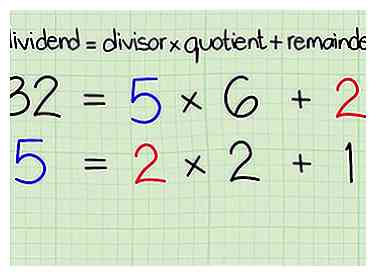 8 Schrijf het algoritme opnieuw uit, maar gebruik deze keer de oude deler als het nieuwe dividend en B) gebruik de rest als de nieuwe deler.
8 Schrijf het algoritme opnieuw uit, maar gebruik deze keer de oude deler als het nieuwe dividend en B) gebruik de rest als de nieuwe deler.  9 Herhaal de vorige stap totdat de rest nul is.
9 Herhaal de vorige stap totdat de rest nul is.  10 De laatste deler is de grootste gemene deler.
10 De laatste deler is de grootste gemene deler.  11 Hier is een voorbeeld, waarin we de GCD van 108 en 30 proberen te vinden:
11 Hier is een voorbeeld, waarin we de GCD van 108 en 30 proberen te vinden:  12 Let op hoe de 30 en de 18 in de eerste regel van positie wisselen om de tweede regel te maken. Vervolgens verschuiven de 18 en 12 om de derde lijn te maken, en de 12 en 6 shift om de vierde lijn te creëren. De 3, 1, 1 en 2 die het vermenigvuldigingssymbool volgen, verschijnen niet opnieuw. Ze geven aan hoe vaak de deler in het dividend past, dus ze zijn uniek voor elke regel.
12 Let op hoe de 30 en de 18 in de eerste regel van positie wisselen om de tweede regel te maken. Vervolgens verschuiven de 18 en 12 om de derde lijn te maken, en de 12 en 6 shift om de vierde lijn te creëren. De 3, 1, 1 en 2 die het vermenigvuldigingssymbool volgen, verschijnen niet opnieuw. Ze geven aan hoe vaak de deler in het dividend past, dus ze zijn uniek voor elke regel.  1 Laat eventuele negatieve signalen vallen.
1 Laat eventuele negatieve signalen vallen.  2 Zoek de priemfactorisatie van de getallen en noteer ze zoals getoond.
2 Zoek de priemfactorisatie van de getallen en noteer ze zoals getoond. 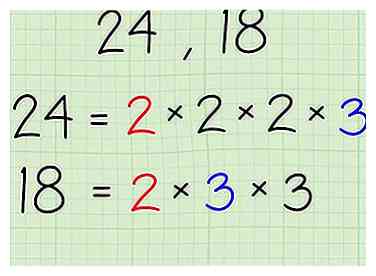 3 Identificeer alle gangbare priemgetallen.
3 Identificeer alle gangbare priemgetallen. 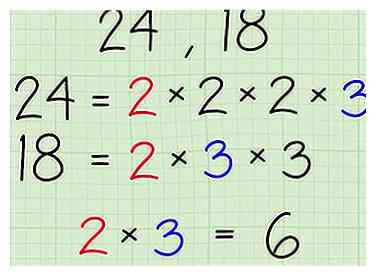 4 Vermenigvuldig de gemeenschappelijke factoren samen.
4 Vermenigvuldig de gemeenschappelijke factoren samen. 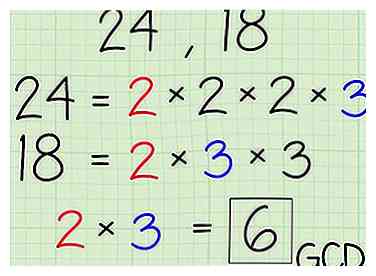 5 Afgewerkt.
5 Afgewerkt.