Prime-factorisatie breekt een aantal uit tot de eenvoudigste bouwstenen. Als je een hekel hebt aan werken met grote getallen zoals 5.733, leer dan hoe je het in plaats daarvan kunt veranderen in 3 x 3 x 7 x 7 x 13. Dit type probleem is van vitaal belang voor cryptografie, of de technieken die worden gebruikt om informatie veilig te houden. Als je nog niet klaar bent om je eigen veilige e-mailsysteem te maken, probeer dan eerst de factor factor te gebruiken om breuken eenvoudiger te maken.
Deel een van de twee:
Het vinden van Prime Factorization
-
 1 Begrijp factorisatie. Factorisatie is het proces waarbij een getal wordt "afgebroken" in kleinere delen. Deze delen of factoren vermenigvuldigen zich met elkaar om het oorspronkelijke aantal te evenaren.
1 Begrijp factorisatie. Factorisatie is het proces waarbij een getal wordt "afgebroken" in kleinere delen. Deze delen of factoren vermenigvuldigen zich met elkaar om het oorspronkelijke aantal te evenaren. - Als u bijvoorbeeld het getal 18 wilt factor, splitst u het in 1 x 18, of in 2 x 9, of in 3 x 6.
-
 2 Recensie van priemgetallen. Een priemgetal heeft slechts twee factoren: zichzelf en 1. Het getal 5 is bijvoorbeeld het product van 5 en 1. U kunt het niet opdelen in andere getallen. Het doel van priemactivatie is om een cijfer te breken totdat er alleen nog priemgetallen over zijn. Dit is vooral handig bij het verwerken van breuken, waardoor ze eenvoudiger te vergelijken en te gebruiken zijn in vergelijkingen.[1]
2 Recensie van priemgetallen. Een priemgetal heeft slechts twee factoren: zichzelf en 1. Het getal 5 is bijvoorbeeld het product van 5 en 1. U kunt het niet opdelen in andere getallen. Het doel van priemactivatie is om een cijfer te breken totdat er alleen nog priemgetallen over zijn. Dit is vooral handig bij het verwerken van breuken, waardoor ze eenvoudiger te vergelijken en te gebruiken zijn in vergelijkingen.[1] -
 3 Begin met een nummer. Kies een niet-priemgetal groter dan 3. Het heeft geen zin om met een priemgetal te beginnen, omdat er geen manier is om dit te factoriseren.
3 Begin met een nummer. Kies een niet-priemgetal groter dan 3. Het heeft geen zin om met een priemgetal te beginnen, omdat er geen manier is om dit te factoriseren. - Voorbeeld: In deze gids vinden we de priemfactorisatie van 24.
-
 4 Factor in twee willekeurige getallen. Zoek naar twee nummers die samen vermenigvuldigen om het nummer te maken waarmee je bent begonnen. U kunt elke twee gebruiken die u maar kunt bedenken, maar een priemgetal zal uw werk gemakkelijker maken. Een goede strategie is om te proberen het getal te delen door 2, dan 3, dan 5, werkend omhoog door de priemgetallen tot je er een vindt die gelijk verdeeld is.
4 Factor in twee willekeurige getallen. Zoek naar twee nummers die samen vermenigvuldigen om het nummer te maken waarmee je bent begonnen. U kunt elke twee gebruiken die u maar kunt bedenken, maar een priemgetal zal uw werk gemakkelijker maken. Een goede strategie is om te proberen het getal te delen door 2, dan 3, dan 5, werkend omhoog door de priemgetallen tot je er een vindt die gelijk verdeeld is. - Voorbeeld: Als je geen factoren van 24 weet, probeer het dan te delen door kleine priemgetallen. Laten we delen door 2 om 24 = te krijgen 2 x 12. We zijn nog niet klaar, maar dit is een goed begin.
- Omdat 2 priem is, is dit een gemakkelijke manier om te beginnen bij het berekenen van een even getal.
-
 5 Begin met het maken van een factorboom. Een factorenboom is een gemakkelijke manier om een factoriseringsprobleem bij te houden.[2] Om er een te beginnen, tekent u gewoon twee "takken" die zich splitsen van het oorspronkelijke nummer. Schrijf uw twee factoren op aan het einde van deze filialen.
5 Begin met het maken van een factorboom. Een factorenboom is een gemakkelijke manier om een factoriseringsprobleem bij te houden.[2] Om er een te beginnen, tekent u gewoon twee "takken" die zich splitsen van het oorspronkelijke nummer. Schrijf uw twee factoren op aan het einde van deze filialen. - Voorbeeld:
- 24
- /\
- 2 12
-
 6 Factor de volgende rij cijfers. Kijk naar je twee nieuwe nummers (de tweede regel op je factorboom). Zijn ze beide prime-lenzen? Als een van hen geen priemgetal is, herhaal het dan op dezelfde manier. Teken meer takken in de boom en schrijf de nieuwe factoren op een derde regel.
6 Factor de volgende rij cijfers. Kijk naar je twee nieuwe nummers (de tweede regel op je factorboom). Zijn ze beide prime-lenzen? Als een van hen geen priemgetal is, herhaal het dan op dezelfde manier. Teken meer takken in de boom en schrijf de nieuwe factoren op een derde regel. - Voorbeeld: 12 is geen prime, dus we factor het opnieuw. Laten we 12 = 2 x 6 gebruiken en toevoegen aan de factorboom:
- 24
- /\
- 2 12
- /\
- 2 x 6
-
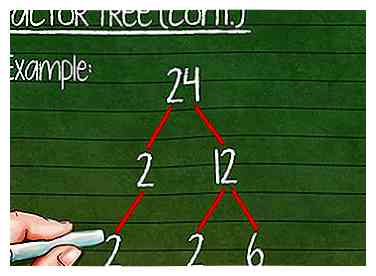 7 Primair neerhalen. Als een van de factoren priem is, breng deze dan naar de volgende regel met zijn eigen enkele 'filiaal'. Er is geen manier om het verder uit te splitsen, dus we houden het nu alleen maar in de gaten.
7 Primair neerhalen. Als een van de factoren priem is, breng deze dan naar de volgende regel met zijn eigen enkele 'filiaal'. Er is geen manier om het verder uit te splitsen, dus we houden het nu alleen maar in de gaten. - Voorbeeld: 2 is een priemgetal. Breng de 2 van de tweede regel naar de derde.
- 24
- /\
- 2 12
- / /\
- 2 2 6
-
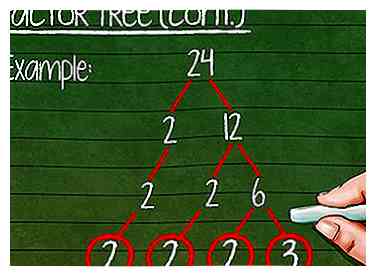 8 Houd rekening met factoring totdat je alleen nog maar priemgetallen overhoudt. Controleer elke nieuwe rij op de factorboom als je het eenmaal hebt geschreven. Als een van de nummers opnieuw kan worden verwerkt, maakt u een nieuwe rij. Je bent klaar als er alleen priemgetallen over zijn.
8 Houd rekening met factoring totdat je alleen nog maar priemgetallen overhoudt. Controleer elke nieuwe rij op de factorboom als je het eenmaal hebt geschreven. Als een van de nummers opnieuw kan worden verwerkt, maakt u een nieuwe rij. Je bent klaar als er alleen priemgetallen over zijn. - Voorbeeld: 6 is een niet-priemgetal en moet opnieuw worden verwerkt. 2 is een priemgetal, dus we brengen de 2s gewoon naar de volgende rij.
- 24
- /\
- 2 12
- / /\
- 2 2 6
- / / /\
- 2 2 2 3
-
 9 Schrijf de laatste regel als uw belangrijkste factoren. Uiteindelijk heb je alleen priemgetallen over. Wanneer dit gebeurt, bent u klaar met factoring. De belangrijkste factorisatie is de volledige, laatste regel getallen, geschreven als een vermenigvuldigingsprobleem.
9 Schrijf de laatste regel als uw belangrijkste factoren. Uiteindelijk heb je alleen priemgetallen over. Wanneer dit gebeurt, bent u klaar met factoring. De belangrijkste factorisatie is de volledige, laatste regel getallen, geschreven als een vermenigvuldigingsprobleem. - Controleer uw werk door de laatste regel samen te vermenigvuldigen. Het moet gelijk zijn aan het originele nummer.
- Voorbeeld: De laatste regel van onze factorboom heeft niets anders dan 2s en 3s. Dit zijn beide prime-lenzen, dus we zijn klaar. We kunnen de primaire ontbinding van 24 als schrijven 24 = 2 x 2 x 2 x 3.
- De volgorde van de factoren doet er niet toe. 2 x 3 x 2 x 2 is ook een goed antwoord.
-
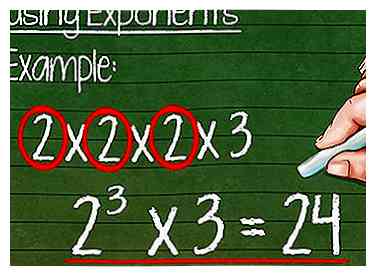 10 Vereenvoudig het gebruik van exponenten (optioneel). Als je weet hoe je exponenten moet schrijven, kun je de prime-factorisatie gemakkelijker te lezen maken. Onthoud dat een exponent een basegetal is, gevolgd door een verheven getal dat aangeeft hoe vaak de basis wordt vermenigvuldigd.
10 Vereenvoudig het gebruik van exponenten (optioneel). Als je weet hoe je exponenten moet schrijven, kun je de prime-factorisatie gemakkelijker te lezen maken. Onthoud dat een exponent een basegetal is, gevolgd door een verheven getal dat aangeeft hoe vaak de basis wordt vermenigvuldigd. - Voorbeeld: In de ontbinding 2 x 2 x 2 x 3, hoe vaak verschijnt 2? Aangezien het antwoord "drie" is, kunnen we 2 x 2 x 2 met 2 vereenvoudigen3. De vereenvoudigde prime-ontbinding is 23 x 3.
Deel twee van twee:
Prime-factorisatie gebruiken
-
 1 Zoek de grootste gemeenschappelijke factor van twee getallen. De grootste gemeenschappelijke factor (GCF) van twee getallen is het grootste getal dat een factor is van beide getallen. U kunt als volgt de GCF van 30 en 36 vinden met behulp van priemfactorisatie:
1 Zoek de grootste gemeenschappelijke factor van twee getallen. De grootste gemeenschappelijke factor (GCF) van twee getallen is het grootste getal dat een factor is van beide getallen. U kunt als volgt de GCF van 30 en 36 vinden met behulp van priemfactorisatie: - Zoek de prime-factorisaties van de twee nummers. De priemfactorisatie van 30 is 2 x 3 x 5. De priemfactorisatie van 36 is 2 x 2 x 3 x 3.
- Zoek een getal dat verschijnt op beide prime-factoren. Doorloop het op elke lijst en schrijf het op een nieuwe regel. Bijvoorbeeld, 2 staat op beide lijsten, dus we schrijven 2 op een nieuwe regel. We blijven over met 30 =
2x 3 x 5 en 36 =2x 2 x 3 x 3. - Herhaal totdat er geen gemeenschappelijke factoren meer zijn. Er staat ook een 3 op beide lijsten, dus schrijf het op je nieuwe regel om te maken 2 en 3. Vergelijk 30 =
2 x 3x 5 en 36 =2x 2 x3x 3. Er zijn geen cijfers meer over. - Om de GCF te vinden, vermenigvuldigt u alle gemeenschappelijke factoren samen. We hebben net 2 en 3 in ons voorbeeld, dus de GCF is 2 x 3 = 6. Dit is het grootste getal dat zowel een factor 30 als een factor 36 is.
-
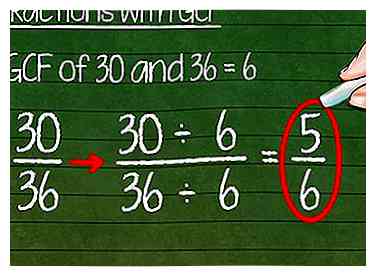 2 Vereenvoudig breuken met de GCF. Gebruik de grootste gemeenschappelijke factor wanneer u vermoedt dat een breuk niet in de eenvoudigste vorm is. Zoek de GCF van de teller en noemer, met behulp van het bovenstaande proces.Zodra u het hebt gevonden, deelt u beide delen van de breuk door de GCF.[3] Het antwoord is dezelfde fractie in eenvoudigste vorm.
2 Vereenvoudig breuken met de GCF. Gebruik de grootste gemeenschappelijke factor wanneer u vermoedt dat een breuk niet in de eenvoudigste vorm is. Zoek de GCF van de teller en noemer, met behulp van het bovenstaande proces.Zodra u het hebt gevonden, deelt u beide delen van de breuk door de GCF.[3] Het antwoord is dezelfde fractie in eenvoudigste vorm. - Vereenvoudig bijvoorbeeld de breuk 30/36. We ontdekten al dat de GCF 6 is, dus deel zowel de teller als de noemer door 6:
- 30 ÷ 6 = 5
- 36 ÷ 6 = 6
- 30/36 = 5/6
-
 3 Zoek het minst veel voorkomende meerdere van twee getallen. Het Least Common Multiple (LCM) van twee getallen is het kleinste getal dat beide van de eerste twee getallen als factoren heeft. De LCM van 2 en 3 is bijvoorbeeld 6, omdat deze zowel 2 als 3 als factoren heeft. Hier is een voorbeeld van het vinden van LCM uit prime-ontbinding:
3 Zoek het minst veel voorkomende meerdere van twee getallen. Het Least Common Multiple (LCM) van twee getallen is het kleinste getal dat beide van de eerste twee getallen als factoren heeft. De LCM van 2 en 3 is bijvoorbeeld 6, omdat deze zowel 2 als 3 als factoren heeft. Hier is een voorbeeld van het vinden van LCM uit prime-ontbinding: - Begin met twee prime-factoren. De priemfactorisatie van 126 is bijvoorbeeld 2 x 3 x 3 x 7. De priemfactorisatie van 84 is 2 x 2 x 3 x 7.
- Vergelijk voor elke unieke factor het aantal keren dat deze in elke lijst voorkomt. Kies een lijst waar deze het grootste aantal keer voorkomt en omcirkel elke instantie. Bijvoorbeeld, 2 verschijnt eenmaal in de factoren 126, maar twee keer in de lijst voor 84. Omcirkel de 2 x 2 in de tweede lijst.
- Herhaal voor elke unieke factor. 3 verschijnt bijvoorbeeld het vaakst in de eerste lijst, dus omcirkel de 3 x 3 er. 7 verschijnt slechts eenmaal op elke lijst, dus omcirkel een single 7. (Het maakt niet uit welke lijst je kiest als er een gelijkspel is.)
- Vermenigvuldig al uw omcirkelde nummers samen om de LCM te vinden. In ons voorbeeld is het kleinste gemene veelvoud van 126 en 84 2 x 2 x 3 x 3 x 7 = 252. Dit is het kleinste getal dat zowel 126 als 84 als factoren heeft.
-
 4 Gebruik de LCM bij het toevoegen van breuken. Voordat u twee breuken bij elkaar kunt optellen, moeten hun noemers hetzelfde zijn. Zoek het kleinste gemeenschappelijke veelvoud van de twee noemers. Vermenigvuldig elke fractie zodat de nieuwe noemer de LCM is. Zodra beide breuken in deze vorm zijn, kunt u ze samen toevoegen.
4 Gebruik de LCM bij het toevoegen van breuken. Voordat u twee breuken bij elkaar kunt optellen, moeten hun noemers hetzelfde zijn. Zoek het kleinste gemeenschappelijke veelvoud van de twee noemers. Vermenigvuldig elke fractie zodat de nieuwe noemer de LCM is. Zodra beide breuken in deze vorm zijn, kunt u ze samen toevoegen. - We willen bijvoorbeeld oplossen 1/6 + 4/21.
- Met behulp van de bovenstaande methode kunnen we de LCM van 6 en 21 vinden. Het antwoord is 42.
- Beurt 1/6 in een breuk met 42 als noemer. Om dit te doen, lost u 42 ÷ 6 = 7. Vermenigvuldigen op 1/6 X 7/7 = 7/42.
- Draaien 4/21 in een breuk met 42 als noemer, los 42 ÷ 21 = 2 op. Vermenigvuldigen 4/21 X 2/2 = 8/42.
- Nu we de breuken in vormen hebben met dezelfde noemer, kunnen we ze gemakkelijk aan elkaar toevoegen: 7/42 + 8/42 = 15/42.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Begrijp factorisatie. Factorisatie is het proces waarbij een getal wordt "afgebroken" in kleinere delen. Deze delen of factoren vermenigvuldigen zich met elkaar om het oorspronkelijke aantal te evenaren.
1 Begrijp factorisatie. Factorisatie is het proces waarbij een getal wordt "afgebroken" in kleinere delen. Deze delen of factoren vermenigvuldigen zich met elkaar om het oorspronkelijke aantal te evenaren.  2 Recensie van priemgetallen. Een priemgetal heeft slechts twee factoren: zichzelf en 1. Het getal 5 is bijvoorbeeld het product van 5 en 1. U kunt het niet opdelen in andere getallen. Het doel van priemactivatie is om een cijfer te breken totdat er alleen nog priemgetallen over zijn. Dit is vooral handig bij het verwerken van breuken, waardoor ze eenvoudiger te vergelijken en te gebruiken zijn in vergelijkingen.[1]
2 Recensie van priemgetallen. Een priemgetal heeft slechts twee factoren: zichzelf en 1. Het getal 5 is bijvoorbeeld het product van 5 en 1. U kunt het niet opdelen in andere getallen. Het doel van priemactivatie is om een cijfer te breken totdat er alleen nog priemgetallen over zijn. Dit is vooral handig bij het verwerken van breuken, waardoor ze eenvoudiger te vergelijken en te gebruiken zijn in vergelijkingen.[1]  3 Begin met een nummer. Kies een niet-priemgetal groter dan 3. Het heeft geen zin om met een priemgetal te beginnen, omdat er geen manier is om dit te factoriseren.
3 Begin met een nummer. Kies een niet-priemgetal groter dan 3. Het heeft geen zin om met een priemgetal te beginnen, omdat er geen manier is om dit te factoriseren.  4 Factor in twee willekeurige getallen. Zoek naar twee nummers die samen vermenigvuldigen om het nummer te maken waarmee je bent begonnen. U kunt elke twee gebruiken die u maar kunt bedenken, maar een priemgetal zal uw werk gemakkelijker maken. Een goede strategie is om te proberen het getal te delen door 2, dan 3, dan 5, werkend omhoog door de priemgetallen tot je er een vindt die gelijk verdeeld is.
4 Factor in twee willekeurige getallen. Zoek naar twee nummers die samen vermenigvuldigen om het nummer te maken waarmee je bent begonnen. U kunt elke twee gebruiken die u maar kunt bedenken, maar een priemgetal zal uw werk gemakkelijker maken. Een goede strategie is om te proberen het getal te delen door 2, dan 3, dan 5, werkend omhoog door de priemgetallen tot je er een vindt die gelijk verdeeld is.  5 Begin met het maken van een factorboom. Een factorenboom is een gemakkelijke manier om een factoriseringsprobleem bij te houden.[2] Om er een te beginnen, tekent u gewoon twee "takken" die zich splitsen van het oorspronkelijke nummer. Schrijf uw twee factoren op aan het einde van deze filialen.
5 Begin met het maken van een factorboom. Een factorenboom is een gemakkelijke manier om een factoriseringsprobleem bij te houden.[2] Om er een te beginnen, tekent u gewoon twee "takken" die zich splitsen van het oorspronkelijke nummer. Schrijf uw twee factoren op aan het einde van deze filialen.  6 Factor de volgende rij cijfers. Kijk naar je twee nieuwe nummers (de tweede regel op je factorboom). Zijn ze beide prime-lenzen? Als een van hen geen priemgetal is, herhaal het dan op dezelfde manier. Teken meer takken in de boom en schrijf de nieuwe factoren op een derde regel.
6 Factor de volgende rij cijfers. Kijk naar je twee nieuwe nummers (de tweede regel op je factorboom). Zijn ze beide prime-lenzen? Als een van hen geen priemgetal is, herhaal het dan op dezelfde manier. Teken meer takken in de boom en schrijf de nieuwe factoren op een derde regel.  7 Primair neerhalen. Als een van de factoren priem is, breng deze dan naar de volgende regel met zijn eigen enkele 'filiaal'. Er is geen manier om het verder uit te splitsen, dus we houden het nu alleen maar in de gaten.
7 Primair neerhalen. Als een van de factoren priem is, breng deze dan naar de volgende regel met zijn eigen enkele 'filiaal'. Er is geen manier om het verder uit te splitsen, dus we houden het nu alleen maar in de gaten.  8 Houd rekening met factoring totdat je alleen nog maar priemgetallen overhoudt. Controleer elke nieuwe rij op de factorboom als je het eenmaal hebt geschreven. Als een van de nummers opnieuw kan worden verwerkt, maakt u een nieuwe rij. Je bent klaar als er alleen priemgetallen over zijn.
8 Houd rekening met factoring totdat je alleen nog maar priemgetallen overhoudt. Controleer elke nieuwe rij op de factorboom als je het eenmaal hebt geschreven. Als een van de nummers opnieuw kan worden verwerkt, maakt u een nieuwe rij. Je bent klaar als er alleen priemgetallen over zijn.  9 Schrijf de laatste regel als uw belangrijkste factoren. Uiteindelijk heb je alleen priemgetallen over. Wanneer dit gebeurt, bent u klaar met factoring. De belangrijkste factorisatie is de volledige, laatste regel getallen, geschreven als een vermenigvuldigingsprobleem.
9 Schrijf de laatste regel als uw belangrijkste factoren. Uiteindelijk heb je alleen priemgetallen over. Wanneer dit gebeurt, bent u klaar met factoring. De belangrijkste factorisatie is de volledige, laatste regel getallen, geschreven als een vermenigvuldigingsprobleem. 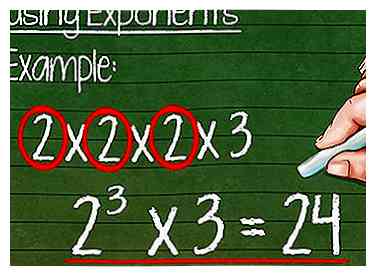 10 Vereenvoudig het gebruik van exponenten (optioneel). Als je weet hoe je exponenten moet schrijven, kun je de prime-factorisatie gemakkelijker te lezen maken. Onthoud dat een exponent een basegetal is, gevolgd door een verheven getal dat aangeeft hoe vaak de basis wordt vermenigvuldigd.
10 Vereenvoudig het gebruik van exponenten (optioneel). Als je weet hoe je exponenten moet schrijven, kun je de prime-factorisatie gemakkelijker te lezen maken. Onthoud dat een exponent een basegetal is, gevolgd door een verheven getal dat aangeeft hoe vaak de basis wordt vermenigvuldigd.  1 Zoek de grootste gemeenschappelijke factor van twee getallen. De grootste gemeenschappelijke factor (GCF) van twee getallen is het grootste getal dat een factor is van beide getallen. U kunt als volgt de GCF van 30 en 36 vinden met behulp van priemfactorisatie:
1 Zoek de grootste gemeenschappelijke factor van twee getallen. De grootste gemeenschappelijke factor (GCF) van twee getallen is het grootste getal dat een factor is van beide getallen. U kunt als volgt de GCF van 30 en 36 vinden met behulp van priemfactorisatie: 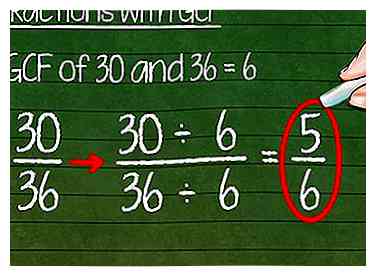 2 Vereenvoudig breuken met de GCF. Gebruik de grootste gemeenschappelijke factor wanneer u vermoedt dat een breuk niet in de eenvoudigste vorm is. Zoek de GCF van de teller en noemer, met behulp van het bovenstaande proces.Zodra u het hebt gevonden, deelt u beide delen van de breuk door de GCF.[3] Het antwoord is dezelfde fractie in eenvoudigste vorm.
2 Vereenvoudig breuken met de GCF. Gebruik de grootste gemeenschappelijke factor wanneer u vermoedt dat een breuk niet in de eenvoudigste vorm is. Zoek de GCF van de teller en noemer, met behulp van het bovenstaande proces.Zodra u het hebt gevonden, deelt u beide delen van de breuk door de GCF.[3] Het antwoord is dezelfde fractie in eenvoudigste vorm.  3 Zoek het minst veel voorkomende meerdere van twee getallen. Het Least Common Multiple (LCM) van twee getallen is het kleinste getal dat beide van de eerste twee getallen als factoren heeft. De LCM van 2 en 3 is bijvoorbeeld 6, omdat deze zowel 2 als 3 als factoren heeft. Hier is een voorbeeld van het vinden van LCM uit prime-ontbinding:
3 Zoek het minst veel voorkomende meerdere van twee getallen. Het Least Common Multiple (LCM) van twee getallen is het kleinste getal dat beide van de eerste twee getallen als factoren heeft. De LCM van 2 en 3 is bijvoorbeeld 6, omdat deze zowel 2 als 3 als factoren heeft. Hier is een voorbeeld van het vinden van LCM uit prime-ontbinding:  4 Gebruik de LCM bij het toevoegen van breuken. Voordat u twee breuken bij elkaar kunt optellen, moeten hun noemers hetzelfde zijn. Zoek het kleinste gemeenschappelijke veelvoud van de twee noemers. Vermenigvuldig elke fractie zodat de nieuwe noemer de LCM is. Zodra beide breuken in deze vorm zijn, kunt u ze samen toevoegen.
4 Gebruik de LCM bij het toevoegen van breuken. Voordat u twee breuken bij elkaar kunt optellen, moeten hun noemers hetzelfde zijn. Zoek het kleinste gemeenschappelijke veelvoud van de twee noemers. Vermenigvuldig elke fractie zodat de nieuwe noemer de LCM is. Zodra beide breuken in deze vorm zijn, kunt u ze samen toevoegen.