Een aantal is factoren zijn getallen die zich vermenigvuldigen om het als een product te vormen. Een andere manier om hieraan te denken is dat elk nummer het product is van meerdere factoren. Leren factor - dat wil zeggen, het opsplitsen van een aantal in zijn samenstellende factoren - is een belangrijke wiskundige vaardigheid die niet alleen wordt gebruikt in elementaire rekenkunde maar ook in algebra, calculus en daarbuiten. Zie stap 1 hieronder om te leren factor te leren!
Methode één van de twee:
Elementaire gehele getallen factoringen
-
 1 Schrijf je nummer op. Om te beginnen met factoring, is alles wat je nodig hebt een getal - elk nummer is voldoende, maar laten we voor onze doeleinden beginnen met een eenvoudig geheel getal. integers zijn getallen zonder breuken of decimale componenten (alle positieve en negatieve hele getallen zijn gehele getallen).
1 Schrijf je nummer op. Om te beginnen met factoring, is alles wat je nodig hebt een getal - elk nummer is voldoende, maar laten we voor onze doeleinden beginnen met een eenvoudig geheel getal. integers zijn getallen zonder breuken of decimale componenten (alle positieve en negatieve hele getallen zijn gehele getallen). - Laten we het nummer kiezen 12. Schrijf dit nummer op een kladpapier.
-
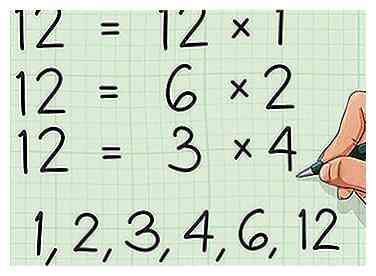 2 Zoek nog twee nummers die zich vermenigvuldigen om je eerste nummer te maken. Elk geheel getal kan worden geschreven als het product van twee andere gehele getallen. Zelfs priemgetallen kunnen worden geschreven als het product van 1 en het nummer zelf. Als je een getal als het product van twee factoren beschouwt, kan dit een 'achterwaarts' denken vereisen - je moet je eigenlijk afvragen: 'welk vermenigvuldigingsprobleem is gelijk aan dit aantal?'
2 Zoek nog twee nummers die zich vermenigvuldigen om je eerste nummer te maken. Elk geheel getal kan worden geschreven als het product van twee andere gehele getallen. Zelfs priemgetallen kunnen worden geschreven als het product van 1 en het nummer zelf. Als je een getal als het product van twee factoren beschouwt, kan dit een 'achterwaarts' denken vereisen - je moet je eigenlijk afvragen: 'welk vermenigvuldigingsprobleem is gelijk aan dit aantal?' - In ons voorbeeld heeft 12 meerdere factoren - 12 × 1, 6 × 2 en 3 × 4 allemaal gelijk 12. We kunnen dus stellen dat de factoren van 12 1, 2, 3, 4, 6 en 12. Laten we voor onze doeleinden werken met de factoren 6 en 2.
- Even getallen zijn vooral gemakkelijk te factoriseren, omdat elk even getal 2 als een factor heeft. 4 = 2 × 2, 26 = 13 × 2, etc.
-
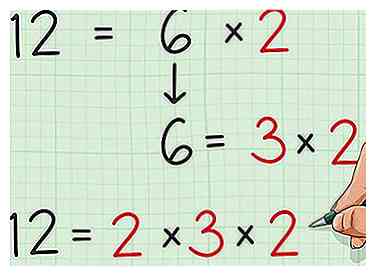 3 Bepaal of een van uw factoren opnieuw kan worden verwerkt. Veel cijfers - vooral grote - kunnen meerdere keren worden verwerkt. Wanneer u twee van de factoren van een getal hebt gevonden, kunt u deze verminderen als u een eigen reeks factoren heeft deze nummer ook voor zijn factoren. Afhankelijk van de situatie kan dit al dan niet gunstig zijn.
3 Bepaal of een van uw factoren opnieuw kan worden verwerkt. Veel cijfers - vooral grote - kunnen meerdere keren worden verwerkt. Wanneer u twee van de factoren van een getal hebt gevonden, kunt u deze verminderen als u een eigen reeks factoren heeft deze nummer ook voor zijn factoren. Afhankelijk van de situatie kan dit al dan niet gunstig zijn. - In ons voorbeeld hebben we bijvoorbeeld 12 tot 2 × 6 gereduceerd. Merk op dat 6 zijn eigen factoren heeft - 3 × 2 = 6. Dus we kunnen zeggen dat 12 = 2 × (3 × 2).
-
 4 Stop met factoring als u priemgetallen bereikt. Primaire getallen zijn getallen groter dan 1 die alleen zelf deelbaar zijn en 1. Bijvoorbeeld 2, 3, 5, 7, 11, 13 en 17 zijn allemaal priemgetallen. Wanneer u een getal hebt meegewogen zodat het het product is van uitsluitend priemgetallen, is verdere factoring overbodig. Het doet je niet goed om elke factor terug te brengen tot keer één keer, dus je kunt stoppen.
4 Stop met factoring als u priemgetallen bereikt. Primaire getallen zijn getallen groter dan 1 die alleen zelf deelbaar zijn en 1. Bijvoorbeeld 2, 3, 5, 7, 11, 13 en 17 zijn allemaal priemgetallen. Wanneer u een getal hebt meegewogen zodat het het product is van uitsluitend priemgetallen, is verdere factoring overbodig. Het doet je niet goed om elke factor terug te brengen tot keer één keer, dus je kunt stoppen. - In ons voorbeeld hebben we 12 tot 2 × (2 × 3) verlaagd. 2, 2 en 3 zijn allemaal priemgetallen. Als we verder zouden werken, zouden we factor (2 × 1) × ((2 × 1) (3 × 1)) moeten hebben, wat meestal niet handig is, dus wordt het meestal vermeden.
-
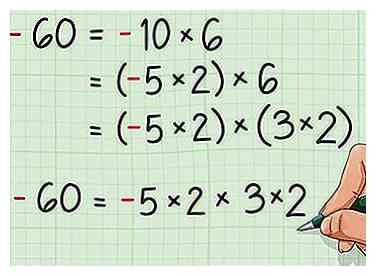 5 Factor negatieve getallen op dezelfde manier. Negatieve getallen kunnen bijna identiek worden verwerkt als hoe positieve getallen worden verwerkt. Het enige verschil is dat de factoren samen moeten vermenigvuldigen om een negatief getal als hun product te maken, dus een oneven aantal van de factoren moet negatief zijn.
5 Factor negatieve getallen op dezelfde manier. Negatieve getallen kunnen bijna identiek worden verwerkt als hoe positieve getallen worden verwerkt. Het enige verschil is dat de factoren samen moeten vermenigvuldigen om een negatief getal als hun product te maken, dus een oneven aantal van de factoren moet negatief zijn. - Laten we bijvoorbeeld factor -60 tellen. Zie hieronder:
- -60 = -10 × 6
- -60 = (-5 × 2) × 6
- -60 = (-5 × 2) × (3 × 2)
- -60 = -5 × 2 × 3 × 2. Merk op dat het hebben van een oneven aantal negatieve getallen naast één hetzelfde product zal geven. Bijvoorbeeld, -5 × 2 × -3 × -2 is ook gelijk aan 60.
- Laten we bijvoorbeeld factor -60 tellen. Zie hieronder:
Methode twee van twee:
Strategie voor het berekenen van grote aantallen
-
 1 Schrijf uw nummer boven een tabel met 2 kolommen. Hoewel het meestal vrij eenvoudig is om hele kleine getallen te factoreren, kunnen grotere aantallen ontmoedigend zijn. De meesten van ons zouden het moeilijk hebben om een 4 of 5-cijferig getal in haar belangrijkste factoren te breken met niets anders dan hoofdrekenen. Gelukkig wordt het proces met een tafel veel eenvoudiger. Schrijf uw nummer boven een t-vormige tafel met twee kolommen - u gebruikt deze tabel om uw groeiende lijst met factoren bij te houden.
1 Schrijf uw nummer boven een tabel met 2 kolommen. Hoewel het meestal vrij eenvoudig is om hele kleine getallen te factoreren, kunnen grotere aantallen ontmoedigend zijn. De meesten van ons zouden het moeilijk hebben om een 4 of 5-cijferig getal in haar belangrijkste factoren te breken met niets anders dan hoofdrekenen. Gelukkig wordt het proces met een tafel veel eenvoudiger. Schrijf uw nummer boven een t-vormige tafel met twee kolommen - u gebruikt deze tabel om uw groeiende lijst met factoren bij te houden. - Laten we voor het doel van ons voorbeeld een 4-cijferig getal kiezen om te factoreren - 6,552.
-
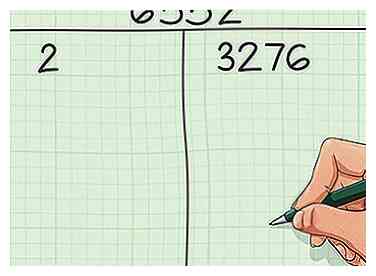 2 Deel uw nummer met de kleinst mogelijke prime-factor. Deel uw nummer met de kleinste prime-factor (naast 1) die gelijk verdeeld is zonder resten. Schrijf de primaire factor in de linkerkolom en schrijf uw antwoord tegenover in de rechterkolom. Zoals hierboven vermeld, zijn even getallen vooral eenvoudig om met factoring te beginnen, omdat hun kleinste prime-factor altijd 2 zal zijn. Oneven getallen zullen daarentegen de kleinste priemfactoren hebben die verschillen.
2 Deel uw nummer met de kleinst mogelijke prime-factor. Deel uw nummer met de kleinste prime-factor (naast 1) die gelijk verdeeld is zonder resten. Schrijf de primaire factor in de linkerkolom en schrijf uw antwoord tegenover in de rechterkolom. Zoals hierboven vermeld, zijn even getallen vooral eenvoudig om met factoring te beginnen, omdat hun kleinste prime-factor altijd 2 zal zijn. Oneven getallen zullen daarentegen de kleinste priemfactoren hebben die verschillen. - In ons voorbeeld, aangezien 6.552 zelfs is, weten we dat 2 de kleinste prime-factor is. 6.552 ÷ 2 = 3.276. In de linkerkolom zullen we schrijven 2, en in de rechterkolom, schrijf 3,276.
-
 3 Blijf op deze manier factor. Formuleer vervolgens het getal in de rechterkolom met de kleinste priemfactor in plaats van het getal bovenaan de tabel. Schrijf de primaire factor in de linkerkolom en het nieuwe nummer in de rechterkolom. Blijf dit proces herhalen - bij elke herhaling moet het aantal in de rechterkolom kleiner worden.
3 Blijf op deze manier factor. Formuleer vervolgens het getal in de rechterkolom met de kleinste priemfactor in plaats van het getal bovenaan de tabel. Schrijf de primaire factor in de linkerkolom en het nieuwe nummer in de rechterkolom. Blijf dit proces herhalen - bij elke herhaling moet het aantal in de rechterkolom kleiner worden. - Laten we doorgaan met ons proces. 3.276 ÷ 2 = 1.638, dus ga naar de onderkant van de linkerkolom, we zullen nog een schrijven 2en onderaan de rechterkolom zullen we schrijven 1,638. 1.638 ÷ 2 = 819, dus we zullen schrijven 2 en 819 onderaan de twee kolommen zoals eerder.
-
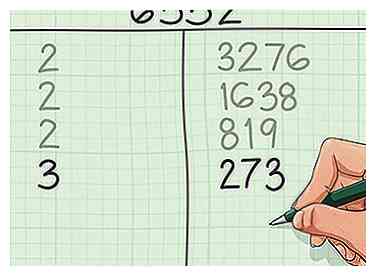 4 Omgaan met oneven nummers door kleine priemfactoren uit te proberen. Oneven getallen zijn moeilijker om de kleinste priemfactor te vinden dan even getallen omdat ze niet automatisch 2 als hun kleinste priemfactor hebben. Wanneer je een oneven getal hebt bereikt, probeer je te delen door kleine priemgetallen anders dan 2 - 3, 5, 7, 11, enzovoort, totdat je er een vindt die gelijk verdeeld is zonder rest. Dit is de kleinste priemfactor van het nummer.
4 Omgaan met oneven nummers door kleine priemfactoren uit te proberen. Oneven getallen zijn moeilijker om de kleinste priemfactor te vinden dan even getallen omdat ze niet automatisch 2 als hun kleinste priemfactor hebben. Wanneer je een oneven getal hebt bereikt, probeer je te delen door kleine priemgetallen anders dan 2 - 3, 5, 7, 11, enzovoort, totdat je er een vindt die gelijk verdeeld is zonder rest. Dit is de kleinste priemfactor van het nummer. - In ons voorbeeld hebben we 819 bereikt. 819 is raar, dus 2 is geen factor 819.In plaats van nog eens 2 op te schrijven, proberen we het volgende priemgetal: 3. 819 ÷ 3 = 273 zonder rest, dus we zullen opschrijven 3 en 273.
- Bij gokfactoren moet je alle priemgetallen proberen tot aan de wortel van de grootste tot nu toe gevonden factor. Als geen van de factoren die u tot nu toe probeert gelijkmatig verdeelt, probeert u waarschijnlijk een priemgetal te berekenen en bent u dus klaar met het factoringproces.
-
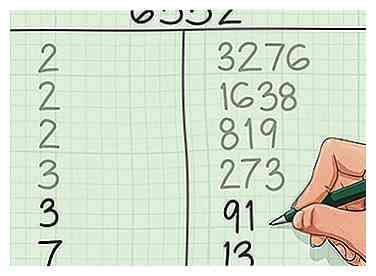 5 Ga verder tot je 1 bereikt. Ga verder met het splitsen van de cijfers in de rechterkolom met hun kleinste prime-factor totdat u een priemgetal in de rechterkolom verkrijgt. Verdeel dit getal zelf - dit plaatst het nummer in de linkerkolom en "1" in de rechterkolom.
5 Ga verder tot je 1 bereikt. Ga verder met het splitsen van de cijfers in de rechterkolom met hun kleinste prime-factor totdat u een priemgetal in de rechterkolom verkrijgt. Verdeel dit getal zelf - dit plaatst het nummer in de linkerkolom en "1" in de rechterkolom. - Laten we afrekenen met het tellen van ons nummer. Zie hieronder voor een gedetailleerde uitsplitsing:
- Deel opnieuw door 3: 273 ÷ 3 = 91, geen rest, dus we zullen opschrijven 3 en 91.
- Laten we opnieuw 3 proberen: 91 heeft geen 3 als een factor, noch heeft het de volgende laagste prime (5) als een factor, maar 91 ÷ 7 = 13, zonder rest, dus we zullen opschrijven 7 en 13.
- Laten we opnieuw 7 proberen: 13 heeft geen 7 als factor, of 11 (de volgende prime), maar het heeft zichzelf als een factor: 13 ÷ 13 = 1. Dus, om onze tafel af te maken, zullen we opschrijven 13 en 1. We kunnen eindelijk stoppen met factoring.
- Laten we afrekenen met het tellen van ons nummer. Zie hieronder voor een gedetailleerde uitsplitsing:
-
 6 Gebruik de cijfers in de linkerkolom als de factoren van uw oorspronkelijke nummer. Zodra je in de rechterkolom 1 hebt bereikt, ben je klaar. De cijfers aan de linkerkant van de tabel zijn uw factoren. Met andere woorden, het product wanneer u al deze getallen samen vermenigvuldigt, is het nummer bovenaan de tabel. Als dezelfde factor meerdere keren wordt weergegeven, kunt u de exponentotatie gebruiken om ruimte te besparen. Als uw lijst met factoren bijvoorbeeld vier 2-en is, kunt u er 2 noteren4 in plaats van 2 × 2 × 2 × 2.
6 Gebruik de cijfers in de linkerkolom als de factoren van uw oorspronkelijke nummer. Zodra je in de rechterkolom 1 hebt bereikt, ben je klaar. De cijfers aan de linkerkant van de tabel zijn uw factoren. Met andere woorden, het product wanneer u al deze getallen samen vermenigvuldigt, is het nummer bovenaan de tabel. Als dezelfde factor meerdere keren wordt weergegeven, kunt u de exponentotatie gebruiken om ruimte te besparen. Als uw lijst met factoren bijvoorbeeld vier 2-en is, kunt u er 2 noteren4 in plaats van 2 × 2 × 2 × 2. - In ons voorbeeld 6,552 = 23 × 32 × 7 × 13. Dit is de volledige ontbinding van 6.552 in priemgetallen. Ongeacht de volgorde waarin deze getallen worden vermenigvuldigd, zal het product 6.552 zijn.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Schrijf je nummer op. Om te beginnen met factoring, is alles wat je nodig hebt een getal - elk nummer is voldoende, maar laten we voor onze doeleinden beginnen met een eenvoudig geheel getal. integers zijn getallen zonder breuken of decimale componenten (alle positieve en negatieve hele getallen zijn gehele getallen).
1 Schrijf je nummer op. Om te beginnen met factoring, is alles wat je nodig hebt een getal - elk nummer is voldoende, maar laten we voor onze doeleinden beginnen met een eenvoudig geheel getal. integers zijn getallen zonder breuken of decimale componenten (alle positieve en negatieve hele getallen zijn gehele getallen). 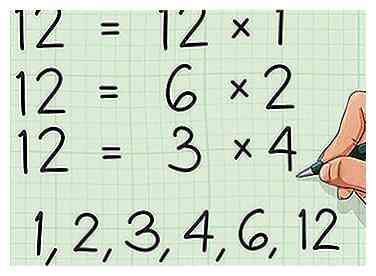 2 Zoek nog twee nummers die zich vermenigvuldigen om je eerste nummer te maken. Elk geheel getal kan worden geschreven als het product van twee andere gehele getallen. Zelfs priemgetallen kunnen worden geschreven als het product van 1 en het nummer zelf. Als je een getal als het product van twee factoren beschouwt, kan dit een 'achterwaarts' denken vereisen - je moet je eigenlijk afvragen: 'welk vermenigvuldigingsprobleem is gelijk aan dit aantal?'
2 Zoek nog twee nummers die zich vermenigvuldigen om je eerste nummer te maken. Elk geheel getal kan worden geschreven als het product van twee andere gehele getallen. Zelfs priemgetallen kunnen worden geschreven als het product van 1 en het nummer zelf. Als je een getal als het product van twee factoren beschouwt, kan dit een 'achterwaarts' denken vereisen - je moet je eigenlijk afvragen: 'welk vermenigvuldigingsprobleem is gelijk aan dit aantal?' 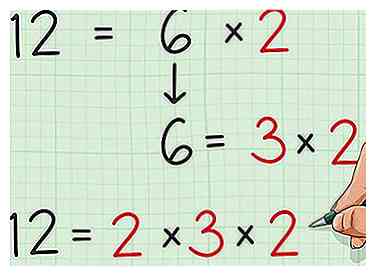 3 Bepaal of een van uw factoren opnieuw kan worden verwerkt. Veel cijfers - vooral grote - kunnen meerdere keren worden verwerkt. Wanneer u twee van de factoren van een getal hebt gevonden, kunt u deze verminderen als u een eigen reeks factoren heeft deze nummer ook voor zijn factoren. Afhankelijk van de situatie kan dit al dan niet gunstig zijn.
3 Bepaal of een van uw factoren opnieuw kan worden verwerkt. Veel cijfers - vooral grote - kunnen meerdere keren worden verwerkt. Wanneer u twee van de factoren van een getal hebt gevonden, kunt u deze verminderen als u een eigen reeks factoren heeft deze nummer ook voor zijn factoren. Afhankelijk van de situatie kan dit al dan niet gunstig zijn.  4 Stop met factoring als u priemgetallen bereikt. Primaire getallen zijn getallen groter dan 1 die alleen zelf deelbaar zijn en 1. Bijvoorbeeld 2, 3, 5, 7, 11, 13 en 17 zijn allemaal priemgetallen. Wanneer u een getal hebt meegewogen zodat het het product is van uitsluitend priemgetallen, is verdere factoring overbodig. Het doet je niet goed om elke factor terug te brengen tot keer één keer, dus je kunt stoppen.
4 Stop met factoring als u priemgetallen bereikt. Primaire getallen zijn getallen groter dan 1 die alleen zelf deelbaar zijn en 1. Bijvoorbeeld 2, 3, 5, 7, 11, 13 en 17 zijn allemaal priemgetallen. Wanneer u een getal hebt meegewogen zodat het het product is van uitsluitend priemgetallen, is verdere factoring overbodig. Het doet je niet goed om elke factor terug te brengen tot keer één keer, dus je kunt stoppen. 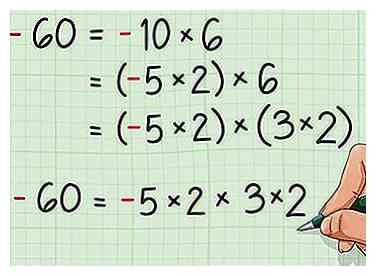 5 Factor negatieve getallen op dezelfde manier. Negatieve getallen kunnen bijna identiek worden verwerkt als hoe positieve getallen worden verwerkt. Het enige verschil is dat de factoren samen moeten vermenigvuldigen om een negatief getal als hun product te maken, dus een oneven aantal van de factoren moet negatief zijn.
5 Factor negatieve getallen op dezelfde manier. Negatieve getallen kunnen bijna identiek worden verwerkt als hoe positieve getallen worden verwerkt. Het enige verschil is dat de factoren samen moeten vermenigvuldigen om een negatief getal als hun product te maken, dus een oneven aantal van de factoren moet negatief zijn.  1 Schrijf uw nummer boven een tabel met 2 kolommen. Hoewel het meestal vrij eenvoudig is om hele kleine getallen te factoreren, kunnen grotere aantallen ontmoedigend zijn. De meesten van ons zouden het moeilijk hebben om een 4 of 5-cijferig getal in haar belangrijkste factoren te breken met niets anders dan hoofdrekenen. Gelukkig wordt het proces met een tafel veel eenvoudiger. Schrijf uw nummer boven een t-vormige tafel met twee kolommen - u gebruikt deze tabel om uw groeiende lijst met factoren bij te houden.
1 Schrijf uw nummer boven een tabel met 2 kolommen. Hoewel het meestal vrij eenvoudig is om hele kleine getallen te factoreren, kunnen grotere aantallen ontmoedigend zijn. De meesten van ons zouden het moeilijk hebben om een 4 of 5-cijferig getal in haar belangrijkste factoren te breken met niets anders dan hoofdrekenen. Gelukkig wordt het proces met een tafel veel eenvoudiger. Schrijf uw nummer boven een t-vormige tafel met twee kolommen - u gebruikt deze tabel om uw groeiende lijst met factoren bij te houden.  2 Deel uw nummer met de kleinst mogelijke prime-factor. Deel uw nummer met de kleinste prime-factor (naast 1) die gelijk verdeeld is zonder resten. Schrijf de primaire factor in de linkerkolom en schrijf uw antwoord tegenover in de rechterkolom. Zoals hierboven vermeld, zijn even getallen vooral eenvoudig om met factoring te beginnen, omdat hun kleinste prime-factor altijd 2 zal zijn. Oneven getallen zullen daarentegen de kleinste priemfactoren hebben die verschillen.
2 Deel uw nummer met de kleinst mogelijke prime-factor. Deel uw nummer met de kleinste prime-factor (naast 1) die gelijk verdeeld is zonder resten. Schrijf de primaire factor in de linkerkolom en schrijf uw antwoord tegenover in de rechterkolom. Zoals hierboven vermeld, zijn even getallen vooral eenvoudig om met factoring te beginnen, omdat hun kleinste prime-factor altijd 2 zal zijn. Oneven getallen zullen daarentegen de kleinste priemfactoren hebben die verschillen.  3 Blijf op deze manier factor. Formuleer vervolgens het getal in de rechterkolom met de kleinste priemfactor in plaats van het getal bovenaan de tabel. Schrijf de primaire factor in de linkerkolom en het nieuwe nummer in de rechterkolom. Blijf dit proces herhalen - bij elke herhaling moet het aantal in de rechterkolom kleiner worden.
3 Blijf op deze manier factor. Formuleer vervolgens het getal in de rechterkolom met de kleinste priemfactor in plaats van het getal bovenaan de tabel. Schrijf de primaire factor in de linkerkolom en het nieuwe nummer in de rechterkolom. Blijf dit proces herhalen - bij elke herhaling moet het aantal in de rechterkolom kleiner worden.  4 Omgaan met oneven nummers door kleine priemfactoren uit te proberen. Oneven getallen zijn moeilijker om de kleinste priemfactor te vinden dan even getallen omdat ze niet automatisch 2 als hun kleinste priemfactor hebben. Wanneer je een oneven getal hebt bereikt, probeer je te delen door kleine priemgetallen anders dan 2 - 3, 5, 7, 11, enzovoort, totdat je er een vindt die gelijk verdeeld is zonder rest. Dit is de kleinste priemfactor van het nummer.
4 Omgaan met oneven nummers door kleine priemfactoren uit te proberen. Oneven getallen zijn moeilijker om de kleinste priemfactor te vinden dan even getallen omdat ze niet automatisch 2 als hun kleinste priemfactor hebben. Wanneer je een oneven getal hebt bereikt, probeer je te delen door kleine priemgetallen anders dan 2 - 3, 5, 7, 11, enzovoort, totdat je er een vindt die gelijk verdeeld is zonder rest. Dit is de kleinste priemfactor van het nummer.  5 Ga verder tot je 1 bereikt. Ga verder met het splitsen van de cijfers in de rechterkolom met hun kleinste prime-factor totdat u een priemgetal in de rechterkolom verkrijgt. Verdeel dit getal zelf - dit plaatst het nummer in de linkerkolom en "1" in de rechterkolom.
5 Ga verder tot je 1 bereikt. Ga verder met het splitsen van de cijfers in de rechterkolom met hun kleinste prime-factor totdat u een priemgetal in de rechterkolom verkrijgt. Verdeel dit getal zelf - dit plaatst het nummer in de linkerkolom en "1" in de rechterkolom.  6 Gebruik de cijfers in de linkerkolom als de factoren van uw oorspronkelijke nummer. Zodra je in de rechterkolom 1 hebt bereikt, ben je klaar. De cijfers aan de linkerkant van de tabel zijn uw factoren. Met andere woorden, het product wanneer u al deze getallen samen vermenigvuldigt, is het nummer bovenaan de tabel. Als dezelfde factor meerdere keren wordt weergegeven, kunt u de exponentotatie gebruiken om ruimte te besparen. Als uw lijst met factoren bijvoorbeeld vier 2-en is, kunt u er 2 noteren4 in plaats van 2 × 2 × 2 × 2.
6 Gebruik de cijfers in de linkerkolom als de factoren van uw oorspronkelijke nummer. Zodra je in de rechterkolom 1 hebt bereikt, ben je klaar. De cijfers aan de linkerkant van de tabel zijn uw factoren. Met andere woorden, het product wanneer u al deze getallen samen vermenigvuldigt, is het nummer bovenaan de tabel. Als dezelfde factor meerdere keren wordt weergegeven, kunt u de exponentotatie gebruiken om ruimte te besparen. Als uw lijst met factoren bijvoorbeeld vier 2-en is, kunt u er 2 noteren4 in plaats van 2 × 2 × 2 × 2.