Problemen met binaire divisies kunnen worden opgelost met behulp van long division, wat een handige methode is om het proces voor jezelf te leren of om een eenvoudig computerprogramma te schrijven. Als alternatief biedt de complementatiemethode van herhaalde aftrekking een aanpak waarmee u misschien niet bekend bent, hoewel deze niet zo vaak wordt gebruikt bij het programmeren.[1] Machinetalen gebruiken over het algemeen een schattingsalgoritme voor meer efficiëntie, maar deze worden hier niet beschreven.[2]
Methode één van de twee:
Long Division gebruiken
-
 1 Review decimale lange divisie. Als het een tijdje geleden is dat je een lange deling met gewone decimale (basis tien) getallen hebt gedaan, bekijk dan de basisbegrippen met het probleem 172 ÷ 4. Anders ga je verder met de volgende stap om hetzelfde proces in binair bestand te leren.
1 Review decimale lange divisie. Als het een tijdje geleden is dat je een lange deling met gewone decimale (basis tien) getallen hebt gedaan, bekijk dan de basisbegrippen met het probleem 172 ÷ 4. Anders ga je verder met de volgende stap om hetzelfde proces in binair bestand te leren. - De dividend is gedeeld door de deler, en het antwoord is de quotiënt.
- Vergelijk de deler met het eerste cijfer in het dividend. Als de deler het grootste getal is, blijf dan cijfers toevoegen aan het dividend totdat de deler het kleinere getal is. (Als we bijvoorbeeld 172 ÷ 4 berekenen, vergelijken we 4 en 1, noteer dat 4> 1 en vergelijk 4 met 17 in plaats daarvan.)
- Schrijf het eerste cijfer van het quotiënt boven het laatste dividendcijfer dat u in de vergelijking gebruikte. Als we 4 en 17 vergelijken, zien we dat 4 vier keer in 17 gaat, dus we schrijven 4 als het eerste cijfer van ons quotiënt, boven de 7.
- Vermenigvuldigen en aftrekken om de rest te vinden. Vermenigvuldig het quotiëntcijfer met de deler, in dit geval 4 x 4 = 16. Schrijf de 16 onder de 17, trek vervolgens 17 - 16 af om de rest te vinden, 1.
- Herhaling. Nogmaals, we vergelijken de deler 4 met het volgende cijfer, 1, merk op dat 4> 1, en "breng" het volgende cijfer van het dividend naar beneden, om 4 te vergelijken met 12 in plaats daarvan. 4 gaat driemaal in 12 keer zonder rest, dus we schrijven 3 als het volgende cijfer van het quotiënt. Het antwoord is 43.
-
 2 Stel het binaire probleem met de langeafstandsverdeling in. Laten we het voorbeeld 10101 ÷ 11 gebruiken. Schrijf dit als een probleem met de lange duur, met de 10101 als het dividend en de 11 als de deler. Laat hierboven ruimte vrij om het quotiënt te schrijven en hieronder om uw berekeningen te schrijven.
2 Stel het binaire probleem met de langeafstandsverdeling in. Laten we het voorbeeld 10101 ÷ 11 gebruiken. Schrijf dit als een probleem met de lange duur, met de 10101 als het dividend en de 11 als de deler. Laat hierboven ruimte vrij om het quotiënt te schrijven en hieronder om uw berekeningen te schrijven. -
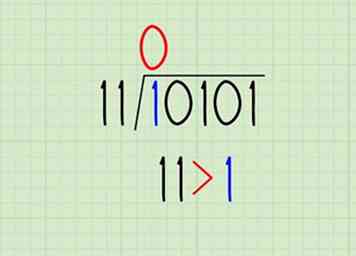 3 Vergelijk de deler met het eerste cijfer van het dividend. Dit werkt net als een decimaal langeafstandsprobleem, maar het is eigenlijk een stuk eenvoudiger in binair. Je kunt het getal niet delen door de deler (0) of de deler kan in één keer worden uitgevoerd (1):
3 Vergelijk de deler met het eerste cijfer van het dividend. Dit werkt net als een decimaal langeafstandsprobleem, maar het is eigenlijk een stuk eenvoudiger in binair. Je kunt het getal niet delen door de deler (0) of de deler kan in één keer worden uitgevoerd (1): - 11> 1, dus 11 kan niet "ingaan" 1. Schrijf een 0 als het eerste cijfer van het quotiënt (boven het eerste cijfer van het dividend).
-
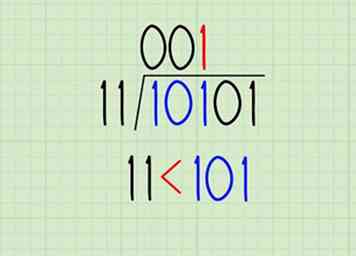 4 Tik op het volgende cijfer en herhaal totdat je een 1 krijgt. Dit zijn de volgende paar stappen naar ons voorbeeld:
4 Tik op het volgende cijfer en herhaal totdat je een 1 krijgt. Dit zijn de volgende paar stappen naar ons voorbeeld: - Breng het volgende cijfer van het dividend naar beneden. 11> 10. Schrijf een 0 in het quotiënt.
- Breng het volgende cijfer naar beneden. 11 <101. Schrijf een 1 in het quotiënt.
-
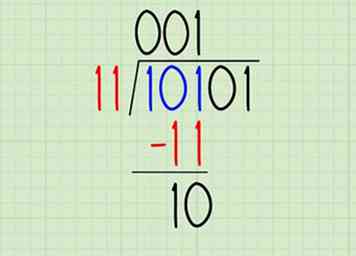 5 Vind de rest. Net als bij decimale lange divisies vermenigvuldigen we het cijfer dat we zojuist hebben gevonden (1) met de deler (11) en schrijven we het resultaat onder ons dividend in lijn met het cijfer dat we net hebben berekend. In het binaire bestand kunnen we dit korter maken, omdat 1 x de deler altijd gelijk is aan de deler:
5 Vind de rest. Net als bij decimale lange divisies vermenigvuldigen we het cijfer dat we zojuist hebben gevonden (1) met de deler (11) en schrijven we het resultaat onder ons dividend in lijn met het cijfer dat we net hebben berekend. In het binaire bestand kunnen we dit korter maken, omdat 1 x de deler altijd gelijk is aan de deler: - Schrijf de deler onder het dividend. Hier schrijven we 11 uitgelijnd onder de eerste drie cijfers (101) van het dividend.
- Bereken 101 - 11 om de rest te krijgen, 10. Kijk hoe u binaire getallen kunt aftrekken als u een beoordeling nodig hebt.
-
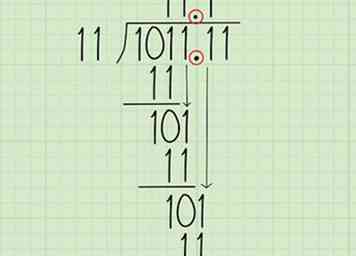
 6 Herhaal totdat het probleem is opgelost. Zet het volgende cijfer van de deler voor de rest omlaag om 100 te maken. Vermeld als 11 <100 een 1 als het volgende cijfer van het quotiënt. Vervolg het probleem als voorheen:
6 Herhaal totdat het probleem is opgelost. Zet het volgende cijfer van de deler voor de rest omlaag om 100 te maken. Vermeld als 11 <100 een 1 als het volgende cijfer van het quotiënt. Vervolg het probleem als voorheen: - Schrijf 11 onder de 100 en trek af om 1 te krijgen.
- Breng het laatste cijfer van het dividend terug tot 11.
- 11 = 11, dus schrijf een 1 als het laatste cijfer van het quotiënt (het antwoord).
- Er is geen rest, dus het probleem is voltooid. Het antwoord is 00111, of gewoon 111.
-
 7 Voeg zo nodig een radixpunt toe. Soms is het resultaat geen geheel getal. Als u nog een rest heeft na het gebruik van het laatste cijfer, voegt u een ".0" toe aan het dividend en een "." naar uw quotiënt, zodat u een ander cijfer kunt verlagen en doorgaan. Herhaal dit totdat je de gewenste specificiteit hebt bereikt en rond dan het antwoord af. Op papier kun je naar beneden afronden door de laatste 0 af te hakken, of als het laatste cijfer een 1 is, laat het vallen en voeg 1 toe aan het nieuwe laatste cijfer. Volg bij het programmeren een van de standaardalgoritmen voor afronding om fouten te voorkomen bij het converteren tussen binaire en decimale getallen.[3]
7 Voeg zo nodig een radixpunt toe. Soms is het resultaat geen geheel getal. Als u nog een rest heeft na het gebruik van het laatste cijfer, voegt u een ".0" toe aan het dividend en een "." naar uw quotiënt, zodat u een ander cijfer kunt verlagen en doorgaan. Herhaal dit totdat je de gewenste specificiteit hebt bereikt en rond dan het antwoord af. Op papier kun je naar beneden afronden door de laatste 0 af te hakken, of als het laatste cijfer een 1 is, laat het vallen en voeg 1 toe aan het nieuwe laatste cijfer. Volg bij het programmeren een van de standaardalgoritmen voor afronding om fouten te voorkomen bij het converteren tussen binaire en decimale getallen.[3] - Binaire deling problemen eindigen vaak met herhalende fractionele delen, vaker dan ze voorkomen in decimale notatie.[4]
- Dit wordt aangeduid met de meer algemene term "radixpunt", die van toepassing is op elke basis, aangezien de "komma" alleen wordt gebruikt in het decimale systeem.[5]
Methode twee van twee:
De complementatiemethode gebruiken
-
 1 Begrijp het basisconcept. Een manier om problemen met divisies op te lossen - op welke basis dan ook - is om de deler van het dividend en vervolgens het restant af te trekken, terwijl je het aantal keren dat je dit kunt doen opvoegt voordat je een negatief getal krijgt. Hier is een voorbeeld in basis tien, het oplossen van het probleem 26 ÷ 7:
1 Begrijp het basisconcept. Een manier om problemen met divisies op te lossen - op welke basis dan ook - is om de deler van het dividend en vervolgens het restant af te trekken, terwijl je het aantal keren dat je dit kunt doen opvoegt voordat je een negatief getal krijgt. Hier is een voorbeeld in basis tien, het oplossen van het probleem 26 ÷ 7: - 26 - 7 = 19 (afgetrokken 1 tijd)
- 19 - 7 = 12 (2)
- 12 - 7 = 5 (3)
- 5 - 7 = -2. Negatief nummer, dus een back-up maken. Het antwoord is 3 met een rest van 5. Merk op dat deze methode geen enkel niet-geheel deel van het antwoord berekent.
-
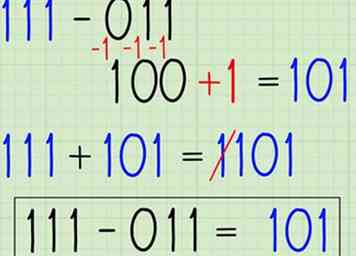 2 Leer aftrekken door complementen. Hoewel u de bovenstaande methode eenvoudig in binair kunt gebruiken, kunnen we ook een efficiëntere methode aftrekken, wat tijd bespaart bij het programmeren van computers om binaire getallen te verdelen. Dit is de aftrekking door de complementsmethode in binair. Hier zijn de basisprincipes, berekening 111 - 011 (zorg ervoor dat beide nummers even lang zijn):
2 Leer aftrekken door complementen. Hoewel u de bovenstaande methode eenvoudig in binair kunt gebruiken, kunnen we ook een efficiëntere methode aftrekken, wat tijd bespaart bij het programmeren van computers om binaire getallen te verdelen. Dit is de aftrekking door de complementsmethode in binair. Hier zijn de basisprincipes, berekening 111 - 011 (zorg ervoor dat beide nummers even lang zijn): - Zoek het complement van de tweede term, waarbij elk cijfer wordt afgetrokken van 1.Dit kan eenvoudig in binair gebeuren door elke 1 naar 0 en elke 0 naar 1 te schakelen.[6][7] In ons voorbeeld wordt 011 100.
- Voeg er een toe aan het resultaat: 100 + 1 = 101. Dit wordt het complement van de tweeën genoemd en laat ons aftrekken als een toevoegingsprobleem uitvoeren.[8] In wezen is het resultaat alsof we een negatief getal toevoegen in plaats van een positief getal af te trekken, zodra we het proces hebben voltooid.
- Voeg het resultaat toe aan de eerste term. Schrijf het probleem op en los het op: 111 + 101 = 1100.
- Gooi het carry-cijfer weg. Gooi het eerste cijfer van je antwoord weg om het eindresultaat te krijgen. 1100 → 100.
-
 3 Combineer de twee bovenstaande concepten. U kent nu de aftrekmethode voor het oplossen van divisieproblemen en de complementmethode van tweeën om aftrekkoppelingen op te lossen. U kunt dit combineren in één methode voor het oplossen van divisieproblemen, met behulp van de onderstaande stappen.[9] Als je wilt, kun je proberen het zelf te bepalen voordat je verder gaat.
3 Combineer de twee bovenstaande concepten. U kent nu de aftrekmethode voor het oplossen van divisieproblemen en de complementmethode van tweeën om aftrekkoppelingen op te lossen. U kunt dit combineren in één methode voor het oplossen van divisieproblemen, met behulp van de onderstaande stappen.[9] Als je wilt, kun je proberen het zelf te bepalen voordat je verder gaat. -
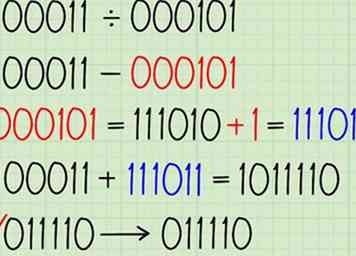 4 Trek de deler van het dividend af door het complement van twee toe te voegen. Laten we het probleem 100011 ÷ 000101 doornemen. De eerste stap is het oplossen van 100011 - 000101, met behulp van de twos 'complement-methode om er een additieprobleem van te maken:
4 Trek de deler van het dividend af door het complement van twee toe te voegen. Laten we het probleem 100011 ÷ 000101 doornemen. De eerste stap is het oplossen van 100011 - 000101, met behulp van de twos 'complement-methode om er een additieprobleem van te maken: - Twos 'complement van 000101 = 111010 + 1 = 111011
- 100011 + 111011 = 1011110
- Draagbit weggooien → 011110
-
 5 Voeg er een toe aan het quotiënt. In een computerprogramma is dit het punt waar je het quotiënt met één verhoogt. Zet op papier ergens in een hoek waar het niet verward zal raken met je andere werk. We hebben met succes een keer afgetrokken, dus het quotiënt tot nu toe is 1.
5 Voeg er een toe aan het quotiënt. In een computerprogramma is dit het punt waar je het quotiënt met één verhoogt. Zet op papier ergens in een hoek waar het niet verward zal raken met je andere werk. We hebben met succes een keer afgetrokken, dus het quotiënt tot nu toe is 1. -
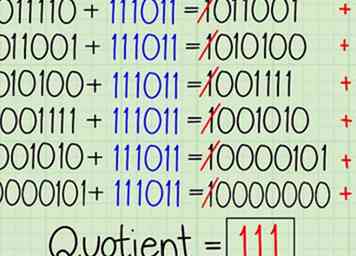 6 Herhaal dit door de deler van de rest af te trekken. Het resultaat van onze laatste berekening is de rest die overblijft nadat de deler eenmaal "in ging". Ga steeds door met het toevoegen van het complement van de deler van de tweeën en het weggooien van de carry-bit. Voeg elke keer een toe aan het quotiënt, herhaal totdat je een rest krijgt die gelijk is aan of kleiner is dan je deler:[10]
6 Herhaal dit door de deler van de rest af te trekken. Het resultaat van onze laatste berekening is de rest die overblijft nadat de deler eenmaal "in ging". Ga steeds door met het toevoegen van het complement van de deler van de tweeën en het weggooien van de carry-bit. Voeg elke keer een toe aan het quotiënt, herhaal totdat je een rest krijgt die gelijk is aan of kleiner is dan je deler:[10] - 011110 + 111011 = 1011001 → 011001 (quotiënt 1+1=10)
- 011001 + 111011 = 1010100 → 010100 (quotiënt 10+1=11)
- 010100 + 111011 = 1001111 → 001111 (11+1=100)
- 001111 + 111011 = 1001010 → 001010 (100+1=101)
- 001010 + 111011 = 10000101 → 0000101 (101+1=110)
- 0000101 + 111011 = 1000000 → 000000 (110+1=111)
- 0 is kleiner dan 101, dus we stoppen hier. Het quotiënt 111 is het antwoord op het afdelingsprobleem. De rest is het eindresultaat van ons aftrekprobleem, in dit geval 0 (geen rest).
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Review decimale lange divisie. Als het een tijdje geleden is dat je een lange deling met gewone decimale (basis tien) getallen hebt gedaan, bekijk dan de basisbegrippen met het probleem 172 ÷ 4. Anders ga je verder met de volgende stap om hetzelfde proces in binair bestand te leren.
1 Review decimale lange divisie. Als het een tijdje geleden is dat je een lange deling met gewone decimale (basis tien) getallen hebt gedaan, bekijk dan de basisbegrippen met het probleem 172 ÷ 4. Anders ga je verder met de volgende stap om hetzelfde proces in binair bestand te leren.  2 Stel het binaire probleem met de langeafstandsverdeling in. Laten we het voorbeeld 10101 ÷ 11 gebruiken. Schrijf dit als een probleem met de lange duur, met de 10101 als het dividend en de 11 als de deler. Laat hierboven ruimte vrij om het quotiënt te schrijven en hieronder om uw berekeningen te schrijven.
2 Stel het binaire probleem met de langeafstandsverdeling in. Laten we het voorbeeld 10101 ÷ 11 gebruiken. Schrijf dit als een probleem met de lange duur, met de 10101 als het dividend en de 11 als de deler. Laat hierboven ruimte vrij om het quotiënt te schrijven en hieronder om uw berekeningen te schrijven. 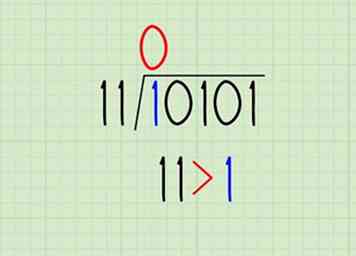 3 Vergelijk de deler met het eerste cijfer van het dividend. Dit werkt net als een decimaal langeafstandsprobleem, maar het is eigenlijk een stuk eenvoudiger in binair. Je kunt het getal niet delen door de deler (0) of de deler kan in één keer worden uitgevoerd (1):
3 Vergelijk de deler met het eerste cijfer van het dividend. Dit werkt net als een decimaal langeafstandsprobleem, maar het is eigenlijk een stuk eenvoudiger in binair. Je kunt het getal niet delen door de deler (0) of de deler kan in één keer worden uitgevoerd (1): 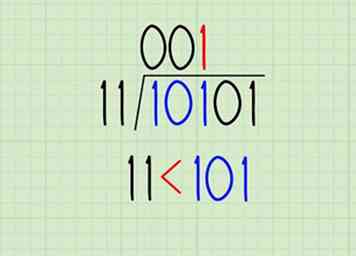 4 Tik op het volgende cijfer en herhaal totdat je een 1 krijgt. Dit zijn de volgende paar stappen naar ons voorbeeld:
4 Tik op het volgende cijfer en herhaal totdat je een 1 krijgt. Dit zijn de volgende paar stappen naar ons voorbeeld: 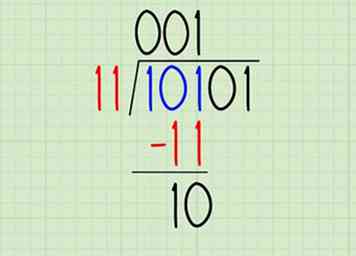 5 Vind de rest. Net als bij decimale lange divisies vermenigvuldigen we het cijfer dat we zojuist hebben gevonden (1) met de deler (11) en schrijven we het resultaat onder ons dividend in lijn met het cijfer dat we net hebben berekend. In het binaire bestand kunnen we dit korter maken, omdat 1 x de deler altijd gelijk is aan de deler:
5 Vind de rest. Net als bij decimale lange divisies vermenigvuldigen we het cijfer dat we zojuist hebben gevonden (1) met de deler (11) en schrijven we het resultaat onder ons dividend in lijn met het cijfer dat we net hebben berekend. In het binaire bestand kunnen we dit korter maken, omdat 1 x de deler altijd gelijk is aan de deler:  6 Herhaal totdat het probleem is opgelost. Zet het volgende cijfer van de deler voor de rest omlaag om 100 te maken. Vermeld als 11 <100 een 1 als het volgende cijfer van het quotiënt. Vervolg het probleem als voorheen:
6 Herhaal totdat het probleem is opgelost. Zet het volgende cijfer van de deler voor de rest omlaag om 100 te maken. Vermeld als 11 <100 een 1 als het volgende cijfer van het quotiënt. Vervolg het probleem als voorheen:  7 Voeg zo nodig een radixpunt toe. Soms is het resultaat geen geheel getal. Als u nog een rest heeft na het gebruik van het laatste cijfer, voegt u een ".0" toe aan het dividend en een "." naar uw quotiënt, zodat u een ander cijfer kunt verlagen en doorgaan. Herhaal dit totdat je de gewenste specificiteit hebt bereikt en rond dan het antwoord af. Op papier kun je naar beneden afronden door de laatste 0 af te hakken, of als het laatste cijfer een 1 is, laat het vallen en voeg 1 toe aan het nieuwe laatste cijfer. Volg bij het programmeren een van de standaardalgoritmen voor afronding om fouten te voorkomen bij het converteren tussen binaire en decimale getallen.[3]
7 Voeg zo nodig een radixpunt toe. Soms is het resultaat geen geheel getal. Als u nog een rest heeft na het gebruik van het laatste cijfer, voegt u een ".0" toe aan het dividend en een "." naar uw quotiënt, zodat u een ander cijfer kunt verlagen en doorgaan. Herhaal dit totdat je de gewenste specificiteit hebt bereikt en rond dan het antwoord af. Op papier kun je naar beneden afronden door de laatste 0 af te hakken, of als het laatste cijfer een 1 is, laat het vallen en voeg 1 toe aan het nieuwe laatste cijfer. Volg bij het programmeren een van de standaardalgoritmen voor afronding om fouten te voorkomen bij het converteren tussen binaire en decimale getallen.[3]  1 Begrijp het basisconcept. Een manier om problemen met divisies op te lossen - op welke basis dan ook - is om de deler van het dividend en vervolgens het restant af te trekken, terwijl je het aantal keren dat je dit kunt doen opvoegt voordat je een negatief getal krijgt. Hier is een voorbeeld in basis tien, het oplossen van het probleem 26 ÷ 7:
1 Begrijp het basisconcept. Een manier om problemen met divisies op te lossen - op welke basis dan ook - is om de deler van het dividend en vervolgens het restant af te trekken, terwijl je het aantal keren dat je dit kunt doen opvoegt voordat je een negatief getal krijgt. Hier is een voorbeeld in basis tien, het oplossen van het probleem 26 ÷ 7: 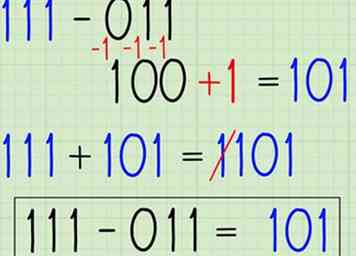 2 Leer aftrekken door complementen. Hoewel u de bovenstaande methode eenvoudig in binair kunt gebruiken, kunnen we ook een efficiëntere methode aftrekken, wat tijd bespaart bij het programmeren van computers om binaire getallen te verdelen. Dit is de aftrekking door de complementsmethode in binair. Hier zijn de basisprincipes, berekening 111 - 011 (zorg ervoor dat beide nummers even lang zijn):
2 Leer aftrekken door complementen. Hoewel u de bovenstaande methode eenvoudig in binair kunt gebruiken, kunnen we ook een efficiëntere methode aftrekken, wat tijd bespaart bij het programmeren van computers om binaire getallen te verdelen. Dit is de aftrekking door de complementsmethode in binair. Hier zijn de basisprincipes, berekening 111 - 011 (zorg ervoor dat beide nummers even lang zijn):  3 Combineer de twee bovenstaande concepten. U kent nu de aftrekmethode voor het oplossen van divisieproblemen en de complementmethode van tweeën om aftrekkoppelingen op te lossen. U kunt dit combineren in één methode voor het oplossen van divisieproblemen, met behulp van de onderstaande stappen.[9] Als je wilt, kun je proberen het zelf te bepalen voordat je verder gaat.
3 Combineer de twee bovenstaande concepten. U kent nu de aftrekmethode voor het oplossen van divisieproblemen en de complementmethode van tweeën om aftrekkoppelingen op te lossen. U kunt dit combineren in één methode voor het oplossen van divisieproblemen, met behulp van de onderstaande stappen.[9] Als je wilt, kun je proberen het zelf te bepalen voordat je verder gaat. 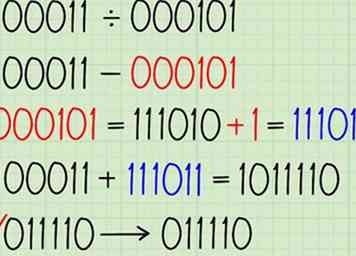 4 Trek de deler van het dividend af door het complement van twee toe te voegen. Laten we het probleem 100011 ÷ 000101 doornemen. De eerste stap is het oplossen van 100011 - 000101, met behulp van de twos 'complement-methode om er een additieprobleem van te maken:
4 Trek de deler van het dividend af door het complement van twee toe te voegen. Laten we het probleem 100011 ÷ 000101 doornemen. De eerste stap is het oplossen van 100011 - 000101, met behulp van de twos 'complement-methode om er een additieprobleem van te maken:  5 Voeg er een toe aan het quotiënt. In een computerprogramma is dit het punt waar je het quotiënt met één verhoogt. Zet op papier ergens in een hoek waar het niet verward zal raken met je andere werk. We hebben met succes een keer afgetrokken, dus het quotiënt tot nu toe is 1.
5 Voeg er een toe aan het quotiënt. In een computerprogramma is dit het punt waar je het quotiënt met één verhoogt. Zet op papier ergens in een hoek waar het niet verward zal raken met je andere werk. We hebben met succes een keer afgetrokken, dus het quotiënt tot nu toe is 1. 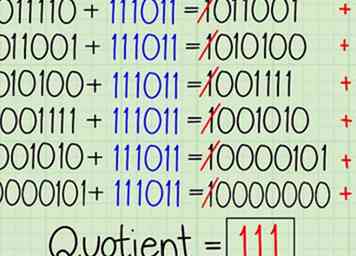 6 Herhaal dit door de deler van de rest af te trekken. Het resultaat van onze laatste berekening is de rest die overblijft nadat de deler eenmaal "in ging". Ga steeds door met het toevoegen van het complement van de deler van de tweeën en het weggooien van de carry-bit. Voeg elke keer een toe aan het quotiënt, herhaal totdat je een rest krijgt die gelijk is aan of kleiner is dan je deler:[10]
6 Herhaal dit door de deler van de rest af te trekken. Het resultaat van onze laatste berekening is de rest die overblijft nadat de deler eenmaal "in ging". Ga steeds door met het toevoegen van het complement van de deler van de tweeën en het weggooien van de carry-bit. Voeg elke keer een toe aan het quotiënt, herhaal totdat je een rest krijgt die gelijk is aan of kleiner is dan je deler:[10]