Cross-vermenigvuldiging is een manier om een vergelijking op te lossen waarbij een variabele betrokken is als onderdeel van twee fracties die aan elkaar gelijk zijn. De variabele is een tijdelijke aanduiding voor een onbekend getal of een onbekende hoeveelheid en cross-vermenigvuldigen vermindert de verhouding tot één eenvoudige vergelijking, waardoor u de variabele in kwestie kunt oplossen. Cross-vermenigvuldigen is vooral handig als u een ratio probeert op te lossen. Hier is hoe het te doen:
Methode één van de twee:
Cross vermenigvuldigen met een enkele variabele
-
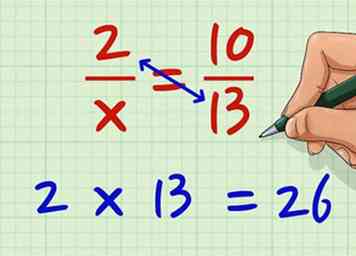 1 Vermenigvuldig de teller van de linkerfractie met de noemer van de rechterfractie. Laten we zeggen dat je aan het werken bent met de vergelijking 2 / x = 10/13. Vermenigvuldig nu 2 * 13. 2 * 13 = 26.
1 Vermenigvuldig de teller van de linkerfractie met de noemer van de rechterfractie. Laten we zeggen dat je aan het werken bent met de vergelijking 2 / x = 10/13. Vermenigvuldig nu 2 * 13. 2 * 13 = 26. -
 2 Vermenigvuldig de teller van de rechterfractie met de noemer van de linkerfractie. Verdeel nu x met 10. x * 10 = 10x. Je kunt eerst in deze richting vermenigvuldigen; het doet er echt niet toe zolang je beide tellers diagonaal van de noemers vermenigvuldigt.
2 Vermenigvuldig de teller van de rechterfractie met de noemer van de linkerfractie. Verdeel nu x met 10. x * 10 = 10x. Je kunt eerst in deze richting vermenigvuldigen; het doet er echt niet toe zolang je beide tellers diagonaal van de noemers vermenigvuldigt. -
 3 Stel de twee producten gelijk aan elkaar. Stel gewoon 26 gelijk aan 10x. 26 = 10x. Het maakt niet uit welk nummer u eerst opgeeft; omdat ze gelijk zijn, kun je ze ongestraft van de ene kant van de vergelijking naar de andere omwisselen, zolang je elke term als geheel behandelt.
3 Stel de twee producten gelijk aan elkaar. Stel gewoon 26 gelijk aan 10x. 26 = 10x. Het maakt niet uit welk nummer u eerst opgeeft; omdat ze gelijk zijn, kun je ze ongestraft van de ene kant van de vergelijking naar de andere omwisselen, zolang je elke term als geheel behandelt. - Dus als u 2 / x = 10/13 voor x probeert op te lossen, heeft u 2 * 13 = x * 10 of 26 = 10x.
-
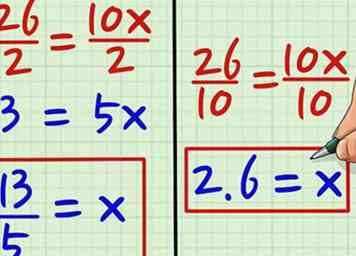 4 Los op voor de variabele. Nu je met 26 = 10x werkt, kun je beginnen met het vinden van een gemeenschappelijke noemer en zowel 26 als 10 delen door een getal dat gelijk verdeeld is in beide getallen. Omdat ze beide even zijn, kun je ze delen door 2; 26/2 = 13 en 10/2 = 5. Je blijft zitten met 13 = 5x. Nu, om x te isoleren, deel beide zijden van de vergelijking door 5. Dus, 13/5 = 5/5, of 13/5 = x. Als u het antwoord in decimale vorm wilt, kunt u beginnen door beide zijden van de vergelijking te delen door 10 om 26/10 = 10/10 of 2,6 = x te krijgen.
4 Los op voor de variabele. Nu je met 26 = 10x werkt, kun je beginnen met het vinden van een gemeenschappelijke noemer en zowel 26 als 10 delen door een getal dat gelijk verdeeld is in beide getallen. Omdat ze beide even zijn, kun je ze delen door 2; 26/2 = 13 en 10/2 = 5. Je blijft zitten met 13 = 5x. Nu, om x te isoleren, deel beide zijden van de vergelijking door 5. Dus, 13/5 = 5/5, of 13/5 = x. Als u het antwoord in decimale vorm wilt, kunt u beginnen door beide zijden van de vergelijking te delen door 10 om 26/10 = 10/10 of 2,6 = x te krijgen.
Methode twee van twee:
Cross vermenigvuldigen met twee van dezelfde variabele
-
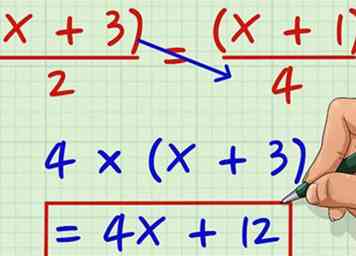 1 Vermenigvuldig de teller van de linkerfractie met de noemer van de rechterfractie. Laten we zeggen dat je met de volgende vergelijking werkt: (x + 3) / 2 = (x + 1) / 4. Vermenigvuldigen (x + 3) door 4 krijgen 4 (x +3). Verspreid de 4 krijgen 4x + 12.
1 Vermenigvuldig de teller van de linkerfractie met de noemer van de rechterfractie. Laten we zeggen dat je met de volgende vergelijking werkt: (x + 3) / 2 = (x + 1) / 4. Vermenigvuldigen (x + 3) door 4 krijgen 4 (x +3). Verspreid de 4 krijgen 4x + 12. -
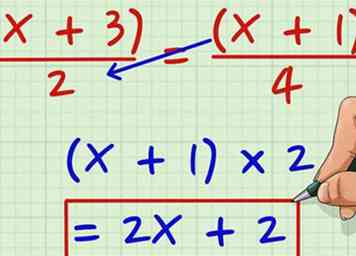 2 Vermenigvuldig de teller van de rechterfractie met de noemer van de linkerfractie. Herhaal het proces aan de andere kant. (x +1) x 2 = 2 (x +1). Verdeel de 2 en je krijgt 2x + 2.
2 Vermenigvuldig de teller van de rechterfractie met de noemer van de linkerfractie. Herhaal het proces aan de andere kant. (x +1) x 2 = 2 (x +1). Verdeel de 2 en je krijgt 2x + 2. -
 3 Stel de twee producten gelijk aan elkaar en combineer soortgelijke termen. Dat heb je nu 4x + 12 = 2x + 2. Combineer de X termen en de constante termen aan weerszijden van de vergelijking.
3 Stel de twee producten gelijk aan elkaar en combineer soortgelijke termen. Dat heb je nu 4x + 12 = 2x + 2. Combineer de X termen en de constante termen aan weerszijden van de vergelijking. - Dus, combineer 4x en 2x door af te trekken 2x van beide kanten. aftrekken 2x van 2x aan de rechterkant zal je 0 achterlaten. Aan de linkerkant, 4x - 2x = 2x, dus jij hebt 2x overgebleven.
- Nu, combineer 12 en 2 door af te trekken 12 van beide kanten van de vergelijking. Aftrekken 12 van 12 aan de linkerkant en je zult 0 hebben, en aftrekken 12 van 2 aan de rechterkant om te krijgen 2-12 = -10.
- Je blijft zitten met 2x = -10.
-
 4 Oplossen. Het enige wat je hoeft te doen is beide kanten van de vergelijking delen door 2. 2x / 2 = -10/2 = x = -5. Na cross-vermenigvuldiging, hebt u vastgesteld dat x = -5. Je kunt teruggaan en je werk controleren door in -5 in te voegen voor x om ervoor te zorgen dat beide zijden van de vergelijking gelijk zijn. Zij zijn. Als je -5 terug in de originele vergelijking plugt, krijg je -1 = -1.
4 Oplossen. Het enige wat je hoeft te doen is beide kanten van de vergelijking delen door 2. 2x / 2 = -10/2 = x = -5. Na cross-vermenigvuldiging, hebt u vastgesteld dat x = -5. Je kunt teruggaan en je werk controleren door in -5 in te voegen voor x om ervoor te zorgen dat beide zijden van de vergelijking gelijk zijn. Zij zijn. Als je -5 terug in de originele vergelijking plugt, krijg je -1 = -1.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
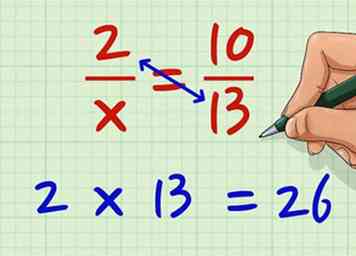 1 Vermenigvuldig de teller van de linkerfractie met de noemer van de rechterfractie. Laten we zeggen dat je aan het werken bent met de vergelijking 2 / x = 10/13. Vermenigvuldig nu 2 * 13. 2 * 13 = 26.
1 Vermenigvuldig de teller van de linkerfractie met de noemer van de rechterfractie. Laten we zeggen dat je aan het werken bent met de vergelijking 2 / x = 10/13. Vermenigvuldig nu 2 * 13. 2 * 13 = 26.  2 Vermenigvuldig de teller van de rechterfractie met de noemer van de linkerfractie. Verdeel nu x met 10. x * 10 = 10x. Je kunt eerst in deze richting vermenigvuldigen; het doet er echt niet toe zolang je beide tellers diagonaal van de noemers vermenigvuldigt.
2 Vermenigvuldig de teller van de rechterfractie met de noemer van de linkerfractie. Verdeel nu x met 10. x * 10 = 10x. Je kunt eerst in deze richting vermenigvuldigen; het doet er echt niet toe zolang je beide tellers diagonaal van de noemers vermenigvuldigt.  3 Stel de twee producten gelijk aan elkaar. Stel gewoon 26 gelijk aan 10x. 26 = 10x. Het maakt niet uit welk nummer u eerst opgeeft; omdat ze gelijk zijn, kun je ze ongestraft van de ene kant van de vergelijking naar de andere omwisselen, zolang je elke term als geheel behandelt.
3 Stel de twee producten gelijk aan elkaar. Stel gewoon 26 gelijk aan 10x. 26 = 10x. Het maakt niet uit welk nummer u eerst opgeeft; omdat ze gelijk zijn, kun je ze ongestraft van de ene kant van de vergelijking naar de andere omwisselen, zolang je elke term als geheel behandelt. 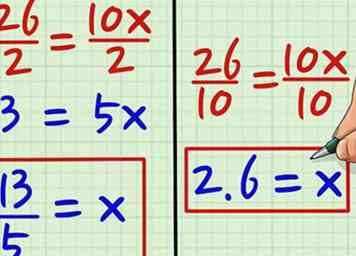 4 Los op voor de variabele. Nu je met 26 = 10x werkt, kun je beginnen met het vinden van een gemeenschappelijke noemer en zowel 26 als 10 delen door een getal dat gelijk verdeeld is in beide getallen. Omdat ze beide even zijn, kun je ze delen door 2; 26/2 = 13 en 10/2 = 5. Je blijft zitten met 13 = 5x. Nu, om x te isoleren, deel beide zijden van de vergelijking door 5. Dus, 13/5 = 5/5, of 13/5 = x. Als u het antwoord in decimale vorm wilt, kunt u beginnen door beide zijden van de vergelijking te delen door 10 om 26/10 = 10/10 of 2,6 = x te krijgen.
4 Los op voor de variabele. Nu je met 26 = 10x werkt, kun je beginnen met het vinden van een gemeenschappelijke noemer en zowel 26 als 10 delen door een getal dat gelijk verdeeld is in beide getallen. Omdat ze beide even zijn, kun je ze delen door 2; 26/2 = 13 en 10/2 = 5. Je blijft zitten met 13 = 5x. Nu, om x te isoleren, deel beide zijden van de vergelijking door 5. Dus, 13/5 = 5/5, of 13/5 = x. Als u het antwoord in decimale vorm wilt, kunt u beginnen door beide zijden van de vergelijking te delen door 10 om 26/10 = 10/10 of 2,6 = x te krijgen. 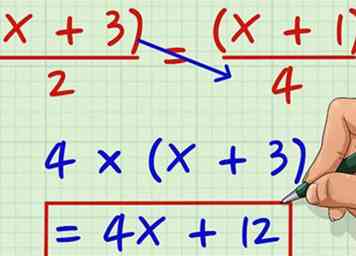 1 Vermenigvuldig de teller van de linkerfractie met de noemer van de rechterfractie. Laten we zeggen dat je met de volgende vergelijking werkt: (x + 3) / 2 = (x + 1) / 4. Vermenigvuldigen (x + 3) door 4 krijgen 4 (x +3). Verspreid de 4 krijgen 4x + 12.
1 Vermenigvuldig de teller van de linkerfractie met de noemer van de rechterfractie. Laten we zeggen dat je met de volgende vergelijking werkt: (x + 3) / 2 = (x + 1) / 4. Vermenigvuldigen (x + 3) door 4 krijgen 4 (x +3). Verspreid de 4 krijgen 4x + 12. 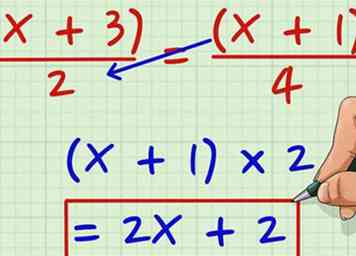 2 Vermenigvuldig de teller van de rechterfractie met de noemer van de linkerfractie. Herhaal het proces aan de andere kant. (x +1) x 2 = 2 (x +1). Verdeel de 2 en je krijgt 2x + 2.
2 Vermenigvuldig de teller van de rechterfractie met de noemer van de linkerfractie. Herhaal het proces aan de andere kant. (x +1) x 2 = 2 (x +1). Verdeel de 2 en je krijgt 2x + 2.  3 Stel de twee producten gelijk aan elkaar en combineer soortgelijke termen. Dat heb je nu 4x + 12 = 2x + 2. Combineer de X termen en de constante termen aan weerszijden van de vergelijking.
3 Stel de twee producten gelijk aan elkaar en combineer soortgelijke termen. Dat heb je nu 4x + 12 = 2x + 2. Combineer de X termen en de constante termen aan weerszijden van de vergelijking.  4 Oplossen. Het enige wat je hoeft te doen is beide kanten van de vergelijking delen door 2. 2x / 2 = -10/2 = x = -5. Na cross-vermenigvuldiging, hebt u vastgesteld dat x = -5. Je kunt teruggaan en je werk controleren door in -5 in te voegen voor x om ervoor te zorgen dat beide zijden van de vergelijking gelijk zijn. Zij zijn. Als je -5 terug in de originele vergelijking plugt, krijg je -1 = -1.
4 Oplossen. Het enige wat je hoeft te doen is beide kanten van de vergelijking delen door 2. 2x / 2 = -10/2 = x = -5. Na cross-vermenigvuldiging, hebt u vastgesteld dat x = -5. Je kunt teruggaan en je werk controleren door in -5 in te voegen voor x om ervoor te zorgen dat beide zijden van de vergelijking gelijk zijn. Zij zijn. Als je -5 terug in de originele vergelijking plugt, krijg je -1 = -1.