Het gebruik van het standaardalgoritme om twee tweecijferige getallen te vermenigvuldigen is voldoende voor de meeste doeleinden; Met de verschillende stappen kunt u echter snel en eenvoudig zoeken naar het product van dit soort nummers. Als u uw wiskundige basiskennis kent en een goede getalwaarneming hebt, kunt u een aantal technieken gebruiken om twee getallen van twee cijfers mentaal te vermenigvuldigen. Als u bekend bent met het verschil van twee vierkanten, kunt u uw twee factoren aanpassen zodat ze passen in deze algebraïsche formule. U kunt de factoren ook manipuleren door de distributieve eigenschap te gebruiken, of door te verdubbelen en te halveren, totdat u twee nieuwe nummers bedenkt waarmee u gemakkelijker kunt werken.
Methode één van de drie:
Het verschil van twee vierkanten vinden
-
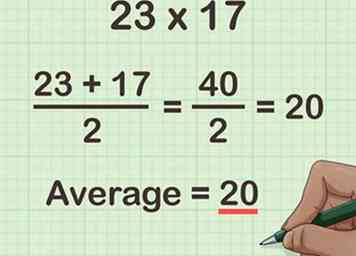 1 Zoek het gemiddelde van de twee factoren die u vermenigvuldigt. Om het gemiddelde te vinden, telt u beide getallen bij elkaar op en deelt u ze vervolgens met 2. U kunt dit ook zien als het getal waarop beide factoren op gelijke afstand liggen.[1]
1 Zoek het gemiddelde van de twee factoren die u vermenigvuldigt. Om het gemiddelde te vinden, telt u beide getallen bij elkaar op en deelt u ze vervolgens met 2. U kunt dit ook zien als het getal waarop beide factoren op gelijke afstand liggen.[1] - Merk op dat deze methode alleen werkt als het gemiddelde van de twee factoren een geheel getal is.
- Bijvoorbeeld als u aan het rekenen bent , vind het gemiddelde van 23 en 17:
Dus het gemiddelde is 20. Met andere woorden, 23 en 17 liggen op gelijke afstand van 20.
-
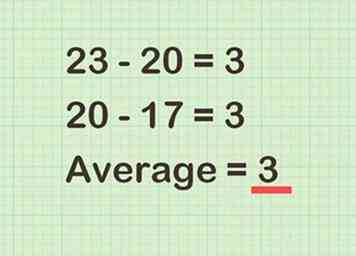 2 Zoek het verschil tussen elke factor en hun gemiddelde. Dit verschil zou voor beide nummers hetzelfde moeten zijn.
2 Zoek het verschil tussen elke factor en hun gemiddelde. Dit verschil zou voor beide nummers hetzelfde moeten zijn. - Omdat het gemiddelde van 23 en 17 bijvoorbeeld 20 is, zou je het berekenen en . Het verschil tussen elke factor en hun gemiddelde is dus 3.
-
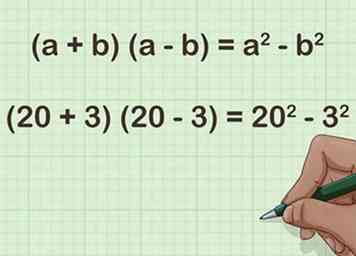 3 Herinner de formule voor het verschil van twee vierkanten. De formule is [2] Voor de vermenigvuldiging van twee getallen van twee cijfers samen, laat gelijk aan het gemiddelde van de twee producten, en gelijk aan het verschil tussen elke factor en hun gemiddelde.[3]
3 Herinner de formule voor het verschil van twee vierkanten. De formule is [2] Voor de vermenigvuldiging van twee getallen van twee cijfers samen, laat gelijk aan het gemiddelde van de twee producten, en gelijk aan het verschil tussen elke factor en hun gemiddelde.[3] - Bijvoorbeeld, .
-
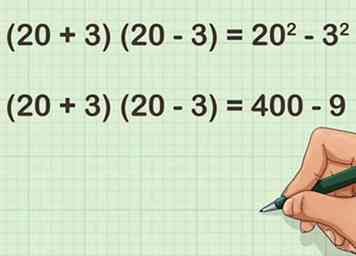 4 Plein en . Onthoud dat het kwadrateren van een getal betekent het alleen vermenigvuldigen. Hopelijk zijn deze getallen gemakkelijk om in je hoofd te zetten. Als dat niet het geval is, moet u mogelijk een andere methode voor mentale wiskunde gebruiken.
4 Plein en . Onthoud dat het kwadrateren van een getal betekent het alleen vermenigvuldigen. Hopelijk zijn deze getallen gemakkelijk om in je hoofd te zetten. Als dat niet het geval is, moet u mogelijk een andere methode voor mentale wiskunde gebruiken. - Bijvoorbeeld:
- Bijvoorbeeld:
-
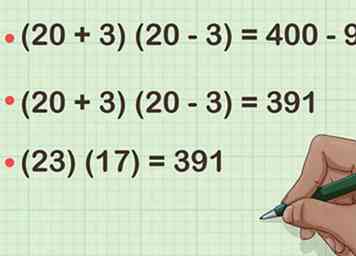 5 Bereken het verschil tussen de twee vierkanten. Het resultaat is het product van uw oorspronkelijke twee factoren.[4]
5 Bereken het verschil tussen de twee vierkanten. Het resultaat is het product van uw oorspronkelijke twee factoren.[4] - Bijvoorbeeld, . Zo, .
Methode twee van drie:
De distributieve eigenschap gebruiken
-
 1 Bepaal welke factor het dichtst bij 100 ligt. Deze methode werkt het beste wanneer een van de factoren bijna 100 is, vooral wanneer een van de factoren 99 is.[5]Maar deze methode kan ook voor andere factoren werken.
1 Bepaal welke factor het dichtst bij 100 ligt. Deze methode werkt het beste wanneer een van de factoren bijna 100 is, vooral wanneer een van de factoren 99 is.[5]Maar deze methode kan ook voor andere factoren werken. - U kunt bijvoorbeeld vermenigvuldigen . In dit geval komt 98 het dichtst bij 100.
-
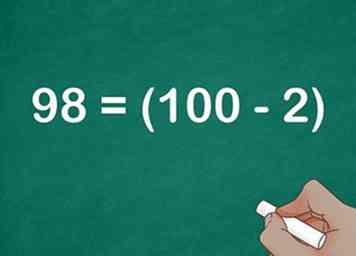 2 Breng de factor die het dichtst bij 100 is, opnieuw tot uitdrukking . De variabele vertegenwoordigt het verschil tussen de factor en 100.[6]
2 Breng de factor die het dichtst bij 100 is, opnieuw tot uitdrukking . De variabele vertegenwoordigt het verschil tussen de factor en 100.[6] - Bijvoorbeeld, .
-
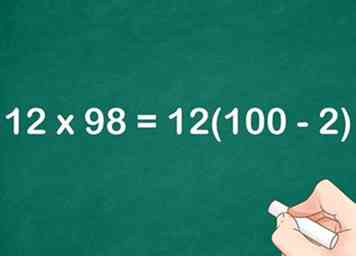 3 Vervang de opnieuw uitgedrukte factor in de oorspronkelijke vergelijking. Je moet nadenken over vermenigvuldigen door de kleinere factor.
3 Vervang de opnieuw uitgedrukte factor in de oorspronkelijke vergelijking. Je moet nadenken over vermenigvuldigen door de kleinere factor. - Bijvoorbeeld, .
-
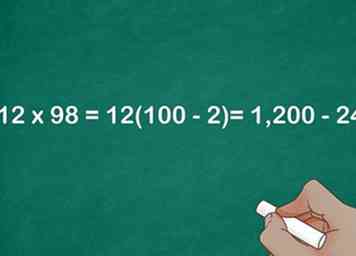 4 Vermenigvuldig het gebruik van de distributieve eigenschap. Omdat het eerste getal tussen haakjes 100 is, zou het gemakkelijk moeten zijn om de eerste factor te vinden. Het vinden van de tweede factor is eenvoudiger als het origineel het dichtst bij 100 komt.
4 Vermenigvuldig het gebruik van de distributieve eigenschap. Omdat het eerste getal tussen haakjes 100 is, zou het gemakkelijk moeten zijn om de eerste factor te vinden. Het vinden van de tweede factor is eenvoudiger als het origineel het dichtst bij 100 komt. - Bijvoorbeeld, .
-
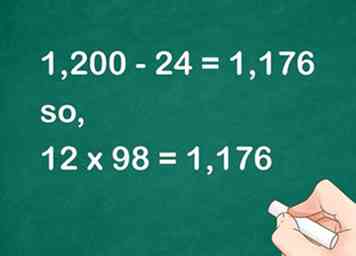 5 Zoek het verschil tussen de twee producten. Dit geeft je het product van je oorspronkelijke twee factoren.[7]
5 Zoek het verschil tussen de twee producten. Dit geeft je het product van je oorspronkelijke twee factoren.[7] - Bijvoorbeeld, , dus .
Methode drie van drie:
Verdubbelen en halveren
-
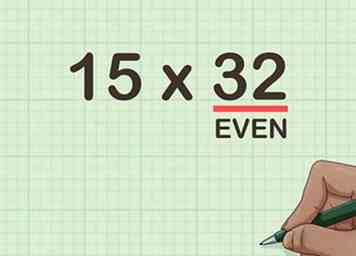 1 Bepaal of beide factoren gelijk zijn. Je halveert het even getal.[8] Onthoud dat een even getal een getal is dat deelbaar is door 2. Als beide factoren gelijk zijn, kies je het kleinere getal dat je wilt halveren.
1 Bepaal of beide factoren gelijk zijn. Je halveert het even getal.[8] Onthoud dat een even getal een getal is dat deelbaar is door 2. Als beide factoren gelijk zijn, kies je het kleinere getal dat je wilt halveren. - Bijvoorbeeld, als u vermenigvuldigt , je zou de 32 halveren omdat het een even getal is.
-
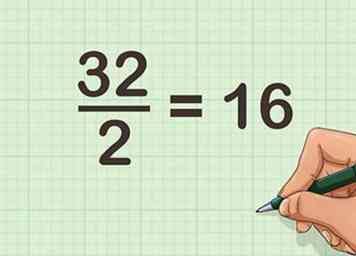 2 De helft van het even aantal. Om dit te doen, deel je door 2. Als je je wiskundige gegevens goed kent, zou je dit gemakkelijk moeten kunnen doen.
2 De helft van het even aantal. Om dit te doen, deel je door 2. Als je je wiskundige gegevens goed kent, zou je dit gemakkelijk moeten kunnen doen. - Bijvoorbeeld, .
-
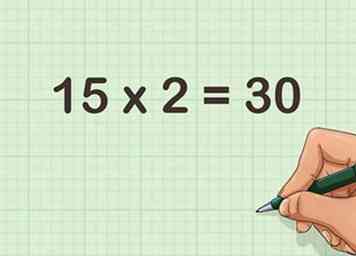 3 Verdubbel het andere nummer. Om een getal te verdubbelen, vermenigvuldigt u het met 2.
3 Verdubbel het andere nummer. Om een getal te verdubbelen, vermenigvuldigt u het met 2. - Bijvoorbeeld, .
-
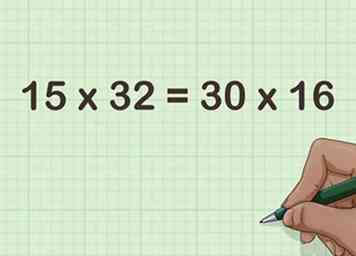 4 Overweeg het nieuwe vermenigvuldigingsprobleem. Het nieuwe probleem is het resultaat van het halveren van een van de factoren en het verdubbelen van de andere.
4 Overweeg het nieuwe vermenigvuldigingsprobleem. Het nieuwe probleem is het resultaat van het halveren van een van de factoren en het verdubbelen van de andere. - Bijvoorbeeld, .
-
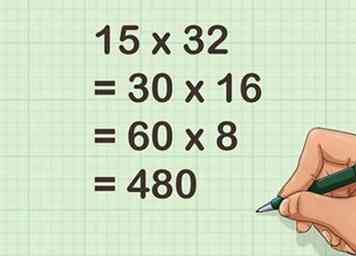 5 Ga door met het proces totdat je een probleem tegenkomt dat je mentaal kunt berekenen. Zorg ervoor dat je altijd hetzelfde aantal halveert en hetzelfde aantal verdubbelt. Het aantal keren dat u halveert en verdubbelt, moet voor beide factoren hetzelfde zijn.[9]
5 Ga door met het proces totdat je een probleem tegenkomt dat je mentaal kunt berekenen. Zorg ervoor dat je altijd hetzelfde aantal halveert en hetzelfde aantal verdubbelt. Het aantal keren dat u halveert en verdubbelt, moet voor beide factoren hetzelfde zijn.[9] - Bijvoorbeeld:
- Bijvoorbeeld:
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
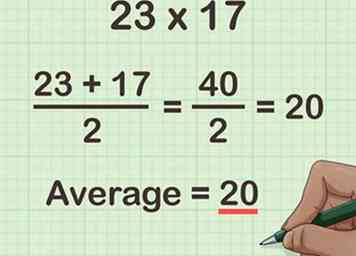 1 Zoek het gemiddelde van de twee factoren die u vermenigvuldigt. Om het gemiddelde te vinden, telt u beide getallen bij elkaar op en deelt u ze vervolgens met 2. U kunt dit ook zien als het getal waarop beide factoren op gelijke afstand liggen.[1]
1 Zoek het gemiddelde van de twee factoren die u vermenigvuldigt. Om het gemiddelde te vinden, telt u beide getallen bij elkaar op en deelt u ze vervolgens met 2. U kunt dit ook zien als het getal waarop beide factoren op gelijke afstand liggen.[1] 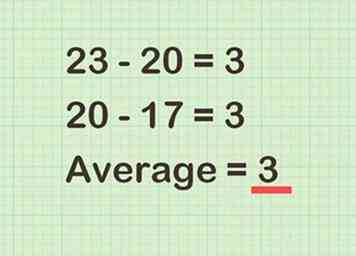 2 Zoek het verschil tussen elke factor en hun gemiddelde. Dit verschil zou voor beide nummers hetzelfde moeten zijn.
2 Zoek het verschil tussen elke factor en hun gemiddelde. Dit verschil zou voor beide nummers hetzelfde moeten zijn. 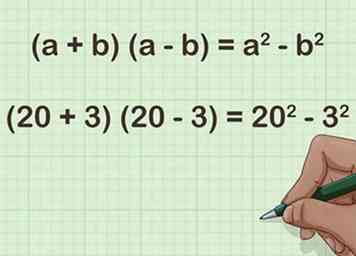 3 Herinner de formule voor het verschil van twee vierkanten. De formule is
3 Herinner de formule voor het verschil van twee vierkanten. De formule is 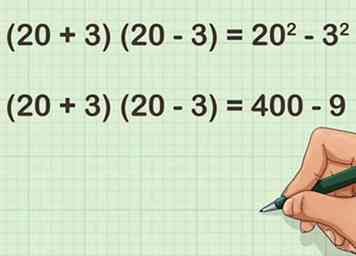 4 Plein
4 Plein 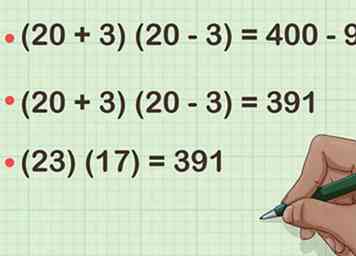 5 Bereken het verschil tussen de twee vierkanten. Het resultaat is het product van uw oorspronkelijke twee factoren.[4]
5 Bereken het verschil tussen de twee vierkanten. Het resultaat is het product van uw oorspronkelijke twee factoren.[4]  1 Bepaal welke factor het dichtst bij 100 ligt. Deze methode werkt het beste wanneer een van de factoren bijna 100 is, vooral wanneer een van de factoren 99 is.[5]Maar deze methode kan ook voor andere factoren werken.
1 Bepaal welke factor het dichtst bij 100 ligt. Deze methode werkt het beste wanneer een van de factoren bijna 100 is, vooral wanneer een van de factoren 99 is.[5]Maar deze methode kan ook voor andere factoren werken. 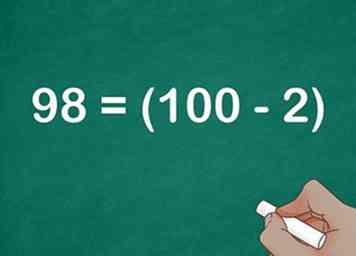 2 Breng de factor die het dichtst bij 100 is, opnieuw tot uitdrukking
2 Breng de factor die het dichtst bij 100 is, opnieuw tot uitdrukking 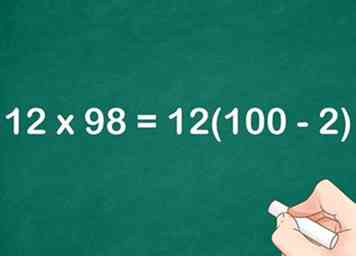 3 Vervang de opnieuw uitgedrukte factor in de oorspronkelijke vergelijking. Je moet nadenken over vermenigvuldigen
3 Vervang de opnieuw uitgedrukte factor in de oorspronkelijke vergelijking. Je moet nadenken over vermenigvuldigen 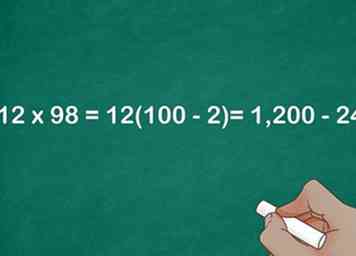 4 Vermenigvuldig het gebruik van de distributieve eigenschap. Omdat het eerste getal tussen haakjes 100 is, zou het gemakkelijk moeten zijn om de eerste factor te vinden. Het vinden van de tweede factor is eenvoudiger als het origineel het dichtst bij 100 komt.
4 Vermenigvuldig het gebruik van de distributieve eigenschap. Omdat het eerste getal tussen haakjes 100 is, zou het gemakkelijk moeten zijn om de eerste factor te vinden. Het vinden van de tweede factor is eenvoudiger als het origineel het dichtst bij 100 komt. 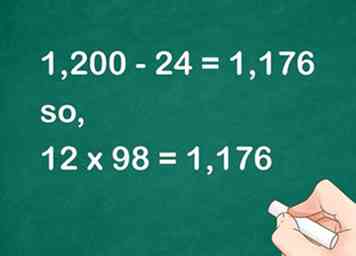 5 Zoek het verschil tussen de twee producten. Dit geeft je het product van je oorspronkelijke twee factoren.[7]
5 Zoek het verschil tussen de twee producten. Dit geeft je het product van je oorspronkelijke twee factoren.[7] 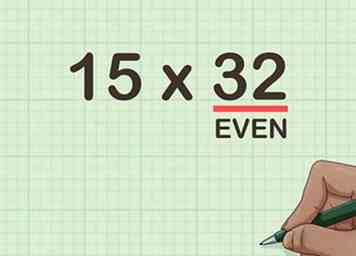 1 Bepaal of beide factoren gelijk zijn. Je halveert het even getal.[8] Onthoud dat een even getal een getal is dat deelbaar is door 2. Als beide factoren gelijk zijn, kies je het kleinere getal dat je wilt halveren.
1 Bepaal of beide factoren gelijk zijn. Je halveert het even getal.[8] Onthoud dat een even getal een getal is dat deelbaar is door 2. Als beide factoren gelijk zijn, kies je het kleinere getal dat je wilt halveren. 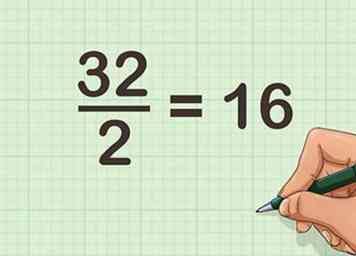 2 De helft van het even aantal. Om dit te doen, deel je door 2. Als je je wiskundige gegevens goed kent, zou je dit gemakkelijk moeten kunnen doen.
2 De helft van het even aantal. Om dit te doen, deel je door 2. Als je je wiskundige gegevens goed kent, zou je dit gemakkelijk moeten kunnen doen. 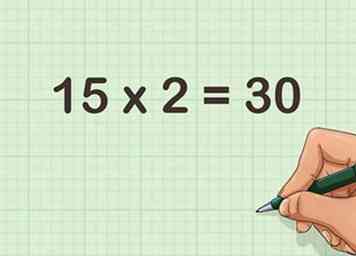 3 Verdubbel het andere nummer. Om een getal te verdubbelen, vermenigvuldigt u het met 2.
3 Verdubbel het andere nummer. Om een getal te verdubbelen, vermenigvuldigt u het met 2. 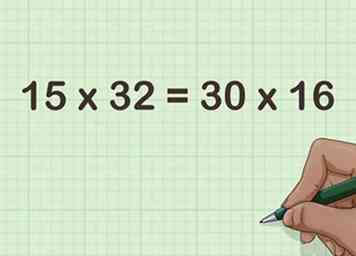 4 Overweeg het nieuwe vermenigvuldigingsprobleem. Het nieuwe probleem is het resultaat van het halveren van een van de factoren en het verdubbelen van de andere.
4 Overweeg het nieuwe vermenigvuldigingsprobleem. Het nieuwe probleem is het resultaat van het halveren van een van de factoren en het verdubbelen van de andere. 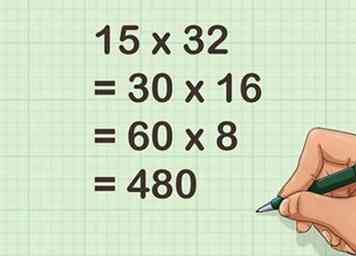 5 Ga door met het proces totdat je een probleem tegenkomt dat je mentaal kunt berekenen. Zorg ervoor dat je altijd hetzelfde aantal halveert en hetzelfde aantal verdubbelt. Het aantal keren dat u halveert en verdubbelt, moet voor beide factoren hetzelfde zijn.[9]
5 Ga door met het proces totdat je een probleem tegenkomt dat je mentaal kunt berekenen. Zorg ervoor dat je altijd hetzelfde aantal halveert en hetzelfde aantal verdubbelt. Het aantal keren dat u halveert en verdubbelt, moet voor beide factoren hetzelfde zijn.[9]