Het radicale symbool (√) vertegenwoordigt de vierkantswortel van een getal. Je kunt het radicale symbool tegenkomen in de algebra of zelfs in het timmerwerk of een andere handel waarbij geometrie betrokken is of relatieve afmetingen of afstanden berekend worden. Je kunt elke twee groepen met dezelfde indices (graden van een wortel) vermenigvuldigen. Als de radicalen niet dezelfde indices hebben, kunt u de vergelijking manipuleren totdat ze dat doen. Als u wilt weten hoe u radicalen vermenigvuldigt met of zonder coëfficiënten, volgt u deze stappen.
Methode één van de drie:
Vermenigvuldig radicalen zonder coëfficiënten
-
 1 Zorg ervoor dat de radicalen dezelfde index hebben. Om radicalen te vermenigvuldigen volgens de basismethode, moeten ze dezelfde index hebben. De "index" is het zeer kleine getal dat net links van de bovenste regel in het radicale symbool is geschreven. Als er geen indexnummer is, wordt de radicaal beschouwd als een vierkantswortel (index 2) en kan deze met andere vierkantswortels worden vermenigvuldigd. Je kunt radicalen met verschillende indices vermenigvuldigen, maar dat is een geavanceerdere methode en zal later worden uitgelegd. Hier zijn twee voorbeelden van vermenigvuldiging met behulp van radicalen met dezelfde indexen:
1 Zorg ervoor dat de radicalen dezelfde index hebben. Om radicalen te vermenigvuldigen volgens de basismethode, moeten ze dezelfde index hebben. De "index" is het zeer kleine getal dat net links van de bovenste regel in het radicale symbool is geschreven. Als er geen indexnummer is, wordt de radicaal beschouwd als een vierkantswortel (index 2) en kan deze met andere vierkantswortels worden vermenigvuldigd. Je kunt radicalen met verschillende indices vermenigvuldigen, maar dat is een geavanceerdere methode en zal later worden uitgelegd. Hier zijn twee voorbeelden van vermenigvuldiging met behulp van radicalen met dezelfde indexen: - Ex. 1: √ (18) x √ (2) =?
- Ex. 2: √ (10) x √ (5) =?
- Ex. 3: 3√ (3) x 3√(9) = ?
-
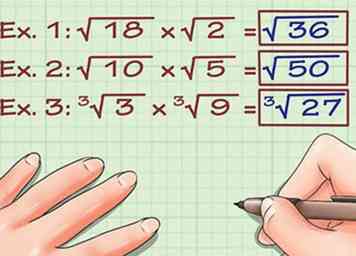 2 Vermenigvuldig de getallen onder de radicale tekens. Vervolgens vermenigvuldigt u eenvoudig de getallen onder de radicale of vierkantswortel tekens en houdt u ze daar. Hier is hoe je het doet:
2 Vermenigvuldig de getallen onder de radicale tekens. Vervolgens vermenigvuldigt u eenvoudig de getallen onder de radicale of vierkantswortel tekens en houdt u ze daar. Hier is hoe je het doet: - Ex. 1: √ (18) x √ (2) = √ (36)
- Ex. 2: √ (10) x √ (5) = √ (50)
- Ex. 3: 3√ (3) x 3√(9) = 3√(27)
-
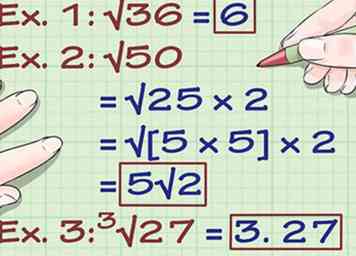 3 Vereenvoudig de radicale expressies. Als je radicalen hebt vermenigvuldigd, is de kans groot dat ze worden vereenvoudigd om perfecte vierkanten of perfecte kubussen te maken, of dat ze kunnen worden vereenvoudigd door een perfect vierkant te vinden als een factor van het eindproduct. Hier is hoe je het doet:
3 Vereenvoudig de radicale expressies. Als je radicalen hebt vermenigvuldigd, is de kans groot dat ze worden vereenvoudigd om perfecte vierkanten of perfecte kubussen te maken, of dat ze kunnen worden vereenvoudigd door een perfect vierkant te vinden als een factor van het eindproduct. Hier is hoe je het doet: - Ex. 1: √ (36) = 6. 36 is een perfect vierkant omdat het het product is van 6 x 6. De vierkantswortel van 36 is eenvoudig 6.
- Ex. 2: √ (50) = √ (25 x 2) = √ ([5 x 5] x 2) = 5√ (2). Hoewel 50 geen perfect vierkant is, is 25 een factor 50 (omdat het gelijk verdeeld is in het getal) en is het een perfect vierkant. Je kunt 25 afbreken in zijn factoren, 5 x 5, en één uit het vierkantswortelbord verplaatsen om de uitdrukking te vereenvoudigen.
- Je kunt het zo zien: als je de 5 teruggooit onder de radicaal, wordt het vermenigvuldigd met zichzelf en wordt het opnieuw 25.
- Ex. 3:3√ (27) = 3. 27 is een perfecte kubus omdat het het product is van 3 x 3 x 3. De kubuswortel van 27 is daarom 3.
Methode twee van drie:
Vermenigvuldig radicalen met coëfficiënten
-
 1 Vermenigvuldig de coëfficiënten. De coëfficiënten zijn de cijfers buiten een radicaal. Als er geen gegeven coëfficiënt is, kan de coëfficiënt worden begrepen als 1. Vermenigvuldig de coëfficiënten samen. Hier is hoe je het doet:
1 Vermenigvuldig de coëfficiënten. De coëfficiënten zijn de cijfers buiten een radicaal. Als er geen gegeven coëfficiënt is, kan de coëfficiënt worden begrepen als 1. Vermenigvuldig de coëfficiënten samen. Hier is hoe je het doet: - Ex. 1: 3√ (2) x √ (10) = 3√ (?)
- 3 x 1 = 3
- Ex. 2: 4√ (3) x 3√ (6) = 12√ (?)
- 4 x 3 = 12
- Ex. 1: 3√ (2) x √ (10) = 3√ (?)
-
 2 Vermenigvuldig de cijfers binnen de radicalen. Nadat u de coëfficiënten hebt vermenigvuldigd, kunt u de getallen binnen de radicalen vermenigvuldigen. Hier is hoe je het doet:
2 Vermenigvuldig de cijfers binnen de radicalen. Nadat u de coëfficiënten hebt vermenigvuldigd, kunt u de getallen binnen de radicalen vermenigvuldigen. Hier is hoe je het doet: - Ex. 1: 3√ (2) x √ (10) = 3√ (2 x 10) = 3√ (20)
- Ex. 2: 4√ (3) x 3√ (6) = 12√ (3 x 6) = 12√ (18)
-
 3 Vereenvoudig het product. Vereenvoudig vervolgens de getallen onder de radicalen door te zoeken naar perfecte vierkanten of veelvouden van de getallen onder de radicalen die perfecte vierkanten zijn. Zodra u die termen hebt vereenvoudigd, kunt u ze gewoon vermenigvuldigen met de bijbehorende coëfficiënten. Hier is hoe je het doet:
3 Vereenvoudig het product. Vereenvoudig vervolgens de getallen onder de radicalen door te zoeken naar perfecte vierkanten of veelvouden van de getallen onder de radicalen die perfecte vierkanten zijn. Zodra u die termen hebt vereenvoudigd, kunt u ze gewoon vermenigvuldigen met de bijbehorende coëfficiënten. Hier is hoe je het doet: - 3√ (20) = 3√ (4 x 5) = 3√ ([2 x 2] x 5) = (3 x 2) √ (5) = 6√ (5)
- 12√ (18) = 12√ (9 x 2) = 12√ (3 x 3 x 2) = (12 x 3) √ (2) = 36√ (2)
Methode drie van drie:
Vermenigvuldig radicalen met verschillende indices
-
 1 Zoek het LCM (laagste gemene veelvoud) van de indices. Zoek het kleinste getal dat gelijkelijk deelbaar is door beide indices om de LCM van de indexen te vinden. Zoek de LCM van de indices voor de volgende vergelijking:3√ (5) x 2√(2) = ?
1 Zoek het LCM (laagste gemene veelvoud) van de indices. Zoek het kleinste getal dat gelijkelijk deelbaar is door beide indices om de LCM van de indexen te vinden. Zoek de LCM van de indices voor de volgende vergelijking:3√ (5) x 2√(2) = ? - De indices zijn 3 en 2. 6 is de LCM van deze twee getallen omdat het het kleinste getal is dat gelijkelijk deelbaar is door zowel 3 als 2. 6/3 = 2 en 6/2 = 3. Om de radicalen te vermenigvuldigen, beide de indices moeten 6 zijn.
-
 2 Schrijf elke expressie met de nieuwe LCM als de index. Hier is hoe de expressies eruit zouden zien in de vergelijking met hun nieuwe indexen:
2 Schrijf elke expressie met de nieuwe LCM als de index. Hier is hoe de expressies eruit zouden zien in de vergelijking met hun nieuwe indexen: - 6√ (5) x 6√(2) = ?
-
 3 Zoek het nummer dat je nodig zou hebben om elke originele index te vermenigvuldigen met om de LCM te vinden. Voor de uitdrukking 3√ (5), je zou de index van 3 bij 2 moeten vermenigvuldigen om 6 te krijgen. Voor de uitdrukking 2√ (2), je zou de index van 2 bij 3 moeten vermenigvuldigen om 6 te krijgen.
3 Zoek het nummer dat je nodig zou hebben om elke originele index te vermenigvuldigen met om de LCM te vinden. Voor de uitdrukking 3√ (5), je zou de index van 3 bij 2 moeten vermenigvuldigen om 6 te krijgen. Voor de uitdrukking 2√ (2), je zou de index van 2 bij 3 moeten vermenigvuldigen om 6 te krijgen. -
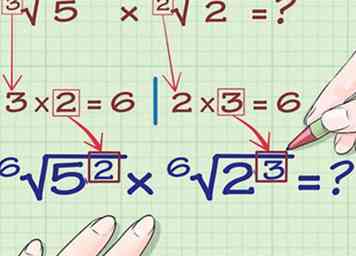 4 Maak van dit nummer de exponent van het getal binnen de radicaal. Maak voor de eerste vergelijking het getal 2 de exponent boven het getal 5. Maak voor de tweede vergelijking het getal 3 de exponent boven het cijfer 2. Dit is hoe het eruit zou zien:
4 Maak van dit nummer de exponent van het getal binnen de radicaal. Maak voor de eerste vergelijking het getal 2 de exponent boven het getal 5. Maak voor de tweede vergelijking het getal 3 de exponent boven het cijfer 2. Dit is hoe het eruit zou zien: - 2 --> 6√(5) = 6√(5)2
- 3 --> 6√(2) = 6√(2)3
-
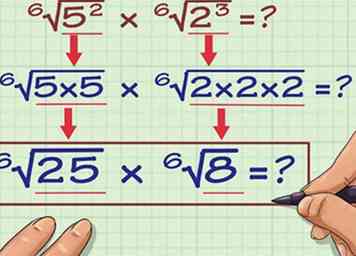 5 Vermenigvuldig de getallen binnen de radicalen met hun exponenten. Hier is hoe je het doet:
5 Vermenigvuldig de getallen binnen de radicalen met hun exponenten. Hier is hoe je het doet: - 6√(5)2 = 6√ (5 x 5) = 6√25
- 6√(2)3 = 6√ (2 x 2 x 2) = 6√8
-
 6 Plaats deze nummers onder één radicaal. Plaats ze onder een radicaal en verbind ze met een vermenigvuldigingsteken. Hier is hoe het resultaat eruit zou zien: 6√ (8 x 25)
6 Plaats deze nummers onder één radicaal. Plaats ze onder een radicaal en verbind ze met een vermenigvuldigingsteken. Hier is hoe het resultaat eruit zou zien: 6√ (8 x 25) -
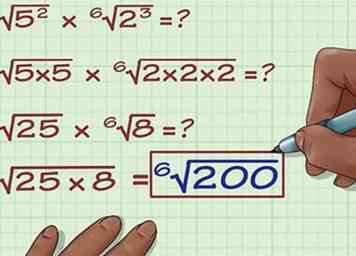 7 Vermenigvuldig ze. 6√ (8 x 25) = 6√ (200). Dit is het laatste antwoord.In sommige gevallen kunt u deze uitdrukkingen mogelijk vereenvoudigen. U kunt deze uitdrukking bijvoorbeeld vereenvoudigen als u een getal hebt gevonden dat zes keer zo veel kan worden vermenigvuldigd als een factor 200. Maar in dit geval kan de uitdrukking niet verder vereenvoudigd worden.
7 Vermenigvuldig ze. 6√ (8 x 25) = 6√ (200). Dit is het laatste antwoord.In sommige gevallen kunt u deze uitdrukkingen mogelijk vereenvoudigen. U kunt deze uitdrukking bijvoorbeeld vereenvoudigen als u een getal hebt gevonden dat zes keer zo veel kan worden vermenigvuldigd als een factor 200. Maar in dit geval kan de uitdrukking niet verder vereenvoudigd worden.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Zorg ervoor dat de radicalen dezelfde index hebben. Om radicalen te vermenigvuldigen volgens de basismethode, moeten ze dezelfde index hebben. De "index" is het zeer kleine getal dat net links van de bovenste regel in het radicale symbool is geschreven. Als er geen indexnummer is, wordt de radicaal beschouwd als een vierkantswortel (index 2) en kan deze met andere vierkantswortels worden vermenigvuldigd. Je kunt radicalen met verschillende indices vermenigvuldigen, maar dat is een geavanceerdere methode en zal later worden uitgelegd. Hier zijn twee voorbeelden van vermenigvuldiging met behulp van radicalen met dezelfde indexen:
1 Zorg ervoor dat de radicalen dezelfde index hebben. Om radicalen te vermenigvuldigen volgens de basismethode, moeten ze dezelfde index hebben. De "index" is het zeer kleine getal dat net links van de bovenste regel in het radicale symbool is geschreven. Als er geen indexnummer is, wordt de radicaal beschouwd als een vierkantswortel (index 2) en kan deze met andere vierkantswortels worden vermenigvuldigd. Je kunt radicalen met verschillende indices vermenigvuldigen, maar dat is een geavanceerdere methode en zal later worden uitgelegd. Hier zijn twee voorbeelden van vermenigvuldiging met behulp van radicalen met dezelfde indexen: 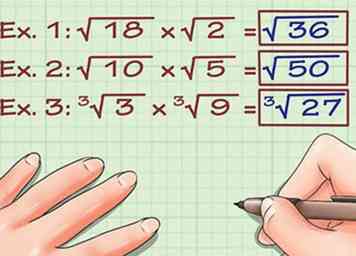 2 Vermenigvuldig de getallen onder de radicale tekens. Vervolgens vermenigvuldigt u eenvoudig de getallen onder de radicale of vierkantswortel tekens en houdt u ze daar. Hier is hoe je het doet:
2 Vermenigvuldig de getallen onder de radicale tekens. Vervolgens vermenigvuldigt u eenvoudig de getallen onder de radicale of vierkantswortel tekens en houdt u ze daar. Hier is hoe je het doet: 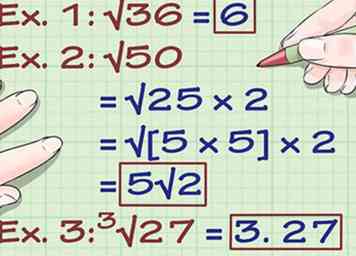 3 Vereenvoudig de radicale expressies. Als je radicalen hebt vermenigvuldigd, is de kans groot dat ze worden vereenvoudigd om perfecte vierkanten of perfecte kubussen te maken, of dat ze kunnen worden vereenvoudigd door een perfect vierkant te vinden als een factor van het eindproduct. Hier is hoe je het doet:
3 Vereenvoudig de radicale expressies. Als je radicalen hebt vermenigvuldigd, is de kans groot dat ze worden vereenvoudigd om perfecte vierkanten of perfecte kubussen te maken, of dat ze kunnen worden vereenvoudigd door een perfect vierkant te vinden als een factor van het eindproduct. Hier is hoe je het doet:  1 Vermenigvuldig de coëfficiënten. De coëfficiënten zijn de cijfers buiten een radicaal. Als er geen gegeven coëfficiënt is, kan de coëfficiënt worden begrepen als 1. Vermenigvuldig de coëfficiënten samen. Hier is hoe je het doet:
1 Vermenigvuldig de coëfficiënten. De coëfficiënten zijn de cijfers buiten een radicaal. Als er geen gegeven coëfficiënt is, kan de coëfficiënt worden begrepen als 1. Vermenigvuldig de coëfficiënten samen. Hier is hoe je het doet:  2 Vermenigvuldig de cijfers binnen de radicalen. Nadat u de coëfficiënten hebt vermenigvuldigd, kunt u de getallen binnen de radicalen vermenigvuldigen. Hier is hoe je het doet:
2 Vermenigvuldig de cijfers binnen de radicalen. Nadat u de coëfficiënten hebt vermenigvuldigd, kunt u de getallen binnen de radicalen vermenigvuldigen. Hier is hoe je het doet:  3 Vereenvoudig het product. Vereenvoudig vervolgens de getallen onder de radicalen door te zoeken naar perfecte vierkanten of veelvouden van de getallen onder de radicalen die perfecte vierkanten zijn. Zodra u die termen hebt vereenvoudigd, kunt u ze gewoon vermenigvuldigen met de bijbehorende coëfficiënten. Hier is hoe je het doet:
3 Vereenvoudig het product. Vereenvoudig vervolgens de getallen onder de radicalen door te zoeken naar perfecte vierkanten of veelvouden van de getallen onder de radicalen die perfecte vierkanten zijn. Zodra u die termen hebt vereenvoudigd, kunt u ze gewoon vermenigvuldigen met de bijbehorende coëfficiënten. Hier is hoe je het doet:  1 Zoek het LCM (laagste gemene veelvoud) van de indices. Zoek het kleinste getal dat gelijkelijk deelbaar is door beide indices om de LCM van de indexen te vinden. Zoek de LCM van de indices voor de volgende vergelijking:3√ (5) x 2√(2) = ?
1 Zoek het LCM (laagste gemene veelvoud) van de indices. Zoek het kleinste getal dat gelijkelijk deelbaar is door beide indices om de LCM van de indexen te vinden. Zoek de LCM van de indices voor de volgende vergelijking:3√ (5) x 2√(2) = ?  2 Schrijf elke expressie met de nieuwe LCM als de index. Hier is hoe de expressies eruit zouden zien in de vergelijking met hun nieuwe indexen:
2 Schrijf elke expressie met de nieuwe LCM als de index. Hier is hoe de expressies eruit zouden zien in de vergelijking met hun nieuwe indexen:  3 Zoek het nummer dat je nodig zou hebben om elke originele index te vermenigvuldigen met om de LCM te vinden. Voor de uitdrukking 3√ (5), je zou de index van 3 bij 2 moeten vermenigvuldigen om 6 te krijgen. Voor de uitdrukking 2√ (2), je zou de index van 2 bij 3 moeten vermenigvuldigen om 6 te krijgen.
3 Zoek het nummer dat je nodig zou hebben om elke originele index te vermenigvuldigen met om de LCM te vinden. Voor de uitdrukking 3√ (5), je zou de index van 3 bij 2 moeten vermenigvuldigen om 6 te krijgen. Voor de uitdrukking 2√ (2), je zou de index van 2 bij 3 moeten vermenigvuldigen om 6 te krijgen. 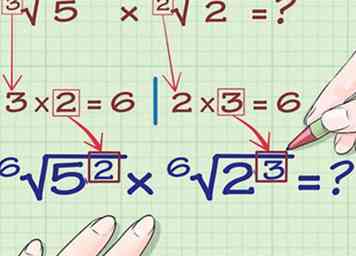 4 Maak van dit nummer de exponent van het getal binnen de radicaal. Maak voor de eerste vergelijking het getal 2 de exponent boven het getal 5. Maak voor de tweede vergelijking het getal 3 de exponent boven het cijfer 2. Dit is hoe het eruit zou zien:
4 Maak van dit nummer de exponent van het getal binnen de radicaal. Maak voor de eerste vergelijking het getal 2 de exponent boven het getal 5. Maak voor de tweede vergelijking het getal 3 de exponent boven het cijfer 2. Dit is hoe het eruit zou zien: 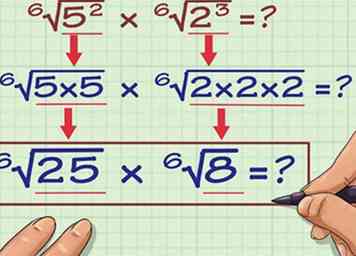 5 Vermenigvuldig de getallen binnen de radicalen met hun exponenten. Hier is hoe je het doet:
5 Vermenigvuldig de getallen binnen de radicalen met hun exponenten. Hier is hoe je het doet:  6 Plaats deze nummers onder één radicaal. Plaats ze onder een radicaal en verbind ze met een vermenigvuldigingsteken. Hier is hoe het resultaat eruit zou zien: 6√ (8 x 25)
6 Plaats deze nummers onder één radicaal. Plaats ze onder een radicaal en verbind ze met een vermenigvuldigingsteken. Hier is hoe het resultaat eruit zou zien: 6√ (8 x 25) 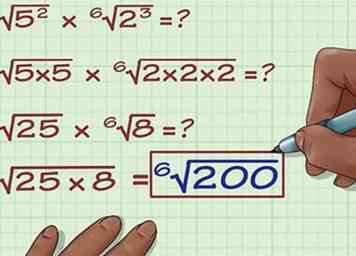 7 Vermenigvuldig ze. 6√ (8 x 25) = 6√ (200). Dit is het laatste antwoord.In sommige gevallen kunt u deze uitdrukkingen mogelijk vereenvoudigen. U kunt deze uitdrukking bijvoorbeeld vereenvoudigen als u een getal hebt gevonden dat zes keer zo veel kan worden vermenigvuldigd als een factor 200. Maar in dit geval kan de uitdrukking niet verder vereenvoudigd worden.
7 Vermenigvuldig ze. 6√ (8 x 25) = 6√ (200). Dit is het laatste antwoord.In sommige gevallen kunt u deze uitdrukkingen mogelijk vereenvoudigen. U kunt deze uitdrukking bijvoorbeeld vereenvoudigen als u een getal hebt gevonden dat zes keer zo veel kan worden vermenigvuldigd als een factor 200. Maar in dit geval kan de uitdrukking niet verder vereenvoudigd worden.