Factorieën, aangegeven met a teken, zijn producten van een geheel getal en alle hele getallen eronder. Het is gemakkelijk om twee factoren te berekenen en te vermenigvuldigen met behulp van een wetenschappelijke rekenmachine functie. U kunt factorfacialen ook met de hand vermenigvuldigen. De eenvoudigste manier om dit te doen is elke factor afzonderlijk te berekenen en vervolgens hun producten samen te vermenigvuldigen. Je kunt ook bepaalde regels van faculteiten gebruiken om gemeenschappelijke factoren naar voren te halen, wat het vermenigvuldigingsproces kan vereenvoudigen.
Methode één van de drie:
Factories begrijpen
-
 1 Identificeer een faculteit. Een faculteit, aangeduid met een geheel getal met een uitroepteken, is het product van een reeks opeenvolgende gehele getallen.[1]
1 Identificeer een faculteit. Een faculteit, aangeduid met een geheel getal met een uitroepteken, is het product van een reeks opeenvolgende gehele getallen.[1] - Bijvoorbeeld, is een faculteit.
-
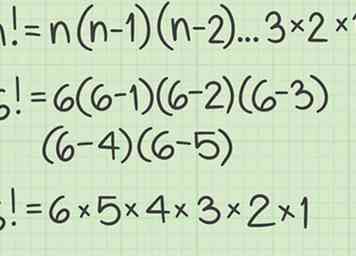 2 Evalueer een faculteit met behulp van een formule. De formule is .[2] Dit betekent dat je de reeks getallen verlengt tot je bij 1 komt.
2 Evalueer een faculteit met behulp van een formule. De formule is .[2] Dit betekent dat je de reeks getallen verlengt tot je bij 1 komt. - Bijvoorbeeld,
-
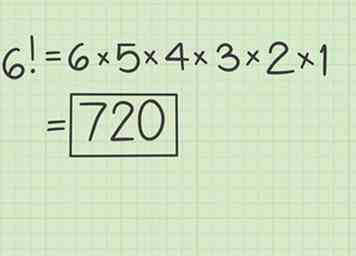 3 Bereken een faculteit. Als u een faculteit wilt berekenen, begint u met het aangegeven getal en vermenigvuldigt u het met elk opeenvolgend geheel getal, tot maximaal 1.[3] Een snelle manier om een faculteit te berekenen is om de toets op een wetenschappelijke rekenmachine. Sla eerst het nummer en druk op de sleutel om het product te zien.
3 Bereken een faculteit. Als u een faculteit wilt berekenen, begint u met het aangegeven getal en vermenigvuldigt u het met elk opeenvolgend geheel getal, tot maximaal 1.[3] Een snelle manier om een faculteit te berekenen is om de toets op een wetenschappelijke rekenmachine. Sla eerst het nummer en druk op de sleutel om het product te zien. - Bijvoorbeeld, .
Methode twee van drie:
Het berekenen van de Factories afzonderlijk
-
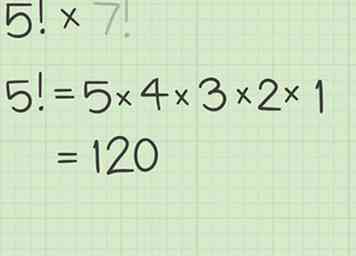 1 Bereken de eerste faculteit. Gebruik een rekenmachine voor grotere aantallen. Als u handmatig handelt, moet u elk volgnummer vermenigvuldigen tot op 1. Herschrijf de vergelijking met dit product tussen haakjes als de eerste factor.
1 Bereken de eerste faculteit. Gebruik een rekenmachine voor grotere aantallen. Als u handmatig handelt, moet u elk volgnummer vermenigvuldigen tot op 1. Herschrijf de vergelijking met dit product tussen haakjes als de eerste factor. - Bijvoorbeeld als u aan het rekenen bent , bereken eerst :
- Bijvoorbeeld als u aan het rekenen bent , bereken eerst :
-
 2 Bereken de tweede faculteit. U kunt dit doen met de rekenmachine of met de hand, te beginnen met de complexiteit van de faculteit. Herschrijf de vergelijking met dit product als de tweede factor.
2 Bereken de tweede faculteit. U kunt dit doen met de rekenmachine of met de hand, te beginnen met de complexiteit van de faculteit. Herschrijf de vergelijking met dit product als de tweede factor. - Bijvoorbeeld:
- Bijvoorbeeld:
-
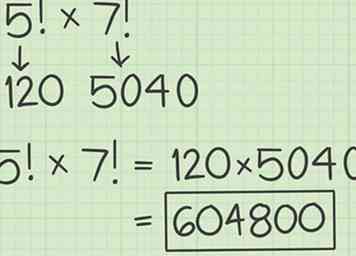 3 Vermenigvuldig de producten van de twee factories. Dit geeft je het product van de twee faculteiten. Omdat factorialen vaak grote aantallen zijn, maakt het gebruik van een rekenmachine deze berekening eenvoudiger.
3 Vermenigvuldig de producten van de twee factories. Dit geeft je het product van de twee faculteiten. Omdat factorialen vaak grote aantallen zijn, maakt het gebruik van een rekenmachine deze berekening eenvoudiger. - Bijvoorbeeld, . Zo, .
Methode drie van drie:
Het vinden van gemeenschappelijke factoren
-
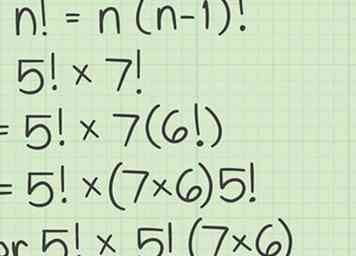 1 Gebruik een formule om de grootste gemeenschappelijke factor te onderscheiden. De formule is . Dit betekent dat een kleinere faculteit een factor is van een grotere faculteit.[4] Bijvoorbeeld, . Wanneer u twee factorialen vermenigvuldigt, is de grootste gemeenschappelijke factor de kleinste van de twee faculteiten.
1 Gebruik een formule om de grootste gemeenschappelijke factor te onderscheiden. De formule is . Dit betekent dat een kleinere faculteit een factor is van een grotere faculteit.[4] Bijvoorbeeld, . Wanneer u twee factorialen vermenigvuldigt, is de grootste gemeenschappelijke factor de kleinste van de twee faculteiten. - Bijvoorbeeld als u aan het rekenen bent , je kunt er rekening mee houden van :
- Bijvoorbeeld als u aan het rekenen bent , je kunt er rekening mee houden van :
-
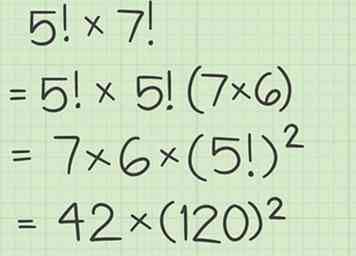 2 Herschrijf de vergelijking en toon de gemeenschappelijke faculteit als een kwadraatwaarde. Bereken vervolgens de faculteit en het kwadraat van het product.
2 Herschrijf de vergelijking en toon de gemeenschappelijke faculteit als een kwadraatwaarde. Bereken vervolgens de faculteit en het kwadraat van het product. - Bijvoorbeeld,
- Bijvoorbeeld,
-
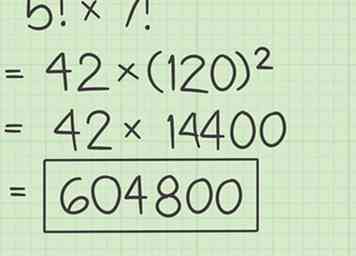 3 Vermenigvuldig de resterende factoren. Het resultaat is het product van de twee oorspronkelijke factorieлlen.
3 Vermenigvuldig de resterende factoren. Het resultaat is het product van de twee oorspronkelijke factorieлlen. - Bijvoorbeeld:
- Bijvoorbeeld:
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Identificeer een faculteit. Een faculteit, aangeduid met een geheel getal met een uitroepteken, is het product van een reeks opeenvolgende gehele getallen.[1]
1 Identificeer een faculteit. Een faculteit, aangeduid met een geheel getal met een uitroepteken, is het product van een reeks opeenvolgende gehele getallen.[1] 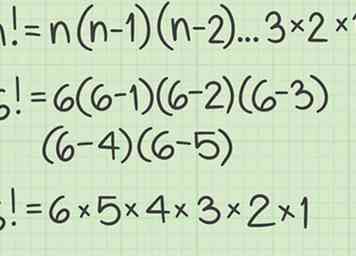 2 Evalueer een faculteit met behulp van een formule. De formule is
2 Evalueer een faculteit met behulp van een formule. De formule is 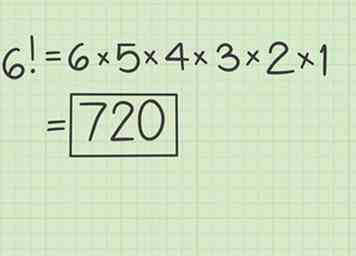 3 Bereken een faculteit. Als u een faculteit wilt berekenen, begint u met het aangegeven getal en vermenigvuldigt u het met elk opeenvolgend geheel getal, tot maximaal 1.[3] Een snelle manier om een faculteit te berekenen is om de
3 Bereken een faculteit. Als u een faculteit wilt berekenen, begint u met het aangegeven getal en vermenigvuldigt u het met elk opeenvolgend geheel getal, tot maximaal 1.[3] Een snelle manier om een faculteit te berekenen is om de 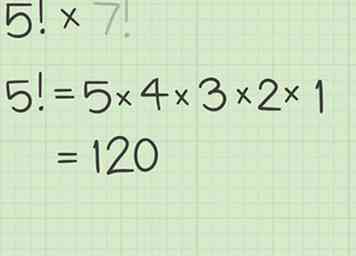 1 Bereken de eerste faculteit. Gebruik een rekenmachine voor grotere aantallen. Als u handmatig handelt, moet u elk volgnummer vermenigvuldigen tot op 1. Herschrijf de vergelijking met dit product tussen haakjes als de eerste factor.
1 Bereken de eerste faculteit. Gebruik een rekenmachine voor grotere aantallen. Als u handmatig handelt, moet u elk volgnummer vermenigvuldigen tot op 1. Herschrijf de vergelijking met dit product tussen haakjes als de eerste factor.  2 Bereken de tweede faculteit. U kunt dit doen met de rekenmachine of met de hand, te beginnen met de complexiteit van de faculteit. Herschrijf de vergelijking met dit product als de tweede factor.
2 Bereken de tweede faculteit. U kunt dit doen met de rekenmachine of met de hand, te beginnen met de complexiteit van de faculteit. Herschrijf de vergelijking met dit product als de tweede factor. 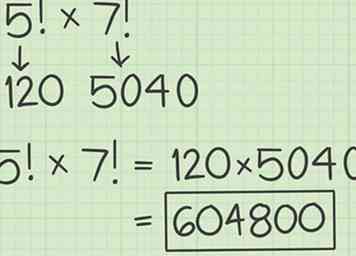 3 Vermenigvuldig de producten van de twee factories. Dit geeft je het product van de twee faculteiten. Omdat factorialen vaak grote aantallen zijn, maakt het gebruik van een rekenmachine deze berekening eenvoudiger.
3 Vermenigvuldig de producten van de twee factories. Dit geeft je het product van de twee faculteiten. Omdat factorialen vaak grote aantallen zijn, maakt het gebruik van een rekenmachine deze berekening eenvoudiger. 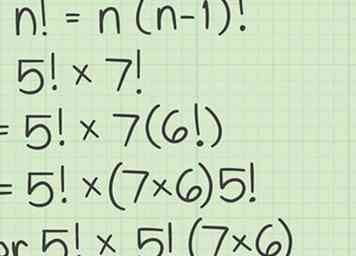 1 Gebruik een formule om de grootste gemeenschappelijke factor te onderscheiden. De formule is
1 Gebruik een formule om de grootste gemeenschappelijke factor te onderscheiden. De formule is 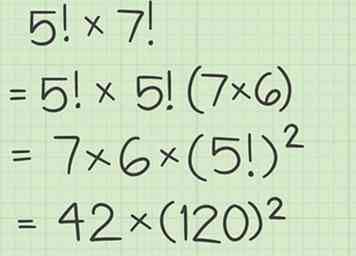 2 Herschrijf de vergelijking en toon de gemeenschappelijke faculteit als een kwadraatwaarde. Bereken vervolgens de faculteit en het kwadraat van het product.
2 Herschrijf de vergelijking en toon de gemeenschappelijke faculteit als een kwadraatwaarde. Bereken vervolgens de faculteit en het kwadraat van het product. 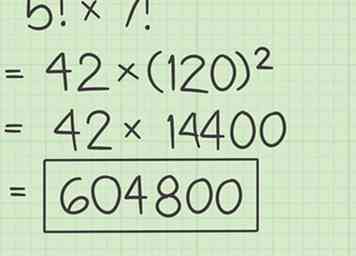 3 Vermenigvuldig de resterende factoren. Het resultaat is het product van de twee oorspronkelijke factorieлlen.
3 Vermenigvuldig de resterende factoren. Het resultaat is het product van de twee oorspronkelijke factorieлlen.