Reciprocals zijn nuttig in allerlei algebraïsche vergelijkingen. Als u bijvoorbeeld de ene breuk door de andere deelt, vermenigvuldigt u de eerste met de wederkerige van de tweede. Je zou ook reciprocals nodig kunnen hebben bij het vinden van vergelijkingen van lijnen.
Methode één van de drie:
De wederkerige van een breuk of geheel getal vinden
-
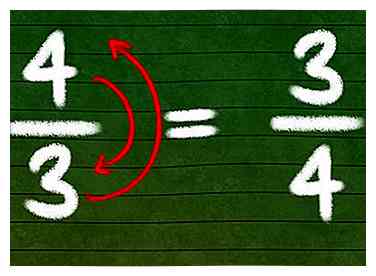 1 Vind de reciproque van een breuk door deze om te draaien. De definitie van "wederzijds" is eenvoudig. Om het omgekeerde van een willekeurig getal te vinden, berekent u gewoon "1 ÷ (dat getal)." Voor een fractie is het omgekeerde slechts een ander deel, met de cijfers omgekeerd (omgekeerd).[1]
1 Vind de reciproque van een breuk door deze om te draaien. De definitie van "wederzijds" is eenvoudig. Om het omgekeerde van een willekeurig getal te vinden, berekent u gewoon "1 ÷ (dat getal)." Voor een fractie is het omgekeerde slechts een ander deel, met de cijfers omgekeerd (omgekeerd).[1] - Bijvoorbeeld het omgekeerde van 3/4 is 4/3.
- Elk aantal keren dat het wederkerig is, geeft u 1.
-
 2 Schrijf de reciproke van een geheel getal als een breuk. Nogmaals, de reciprook van een getal is altijd 1 ÷ (dat aantal). Schrijf voor een heel getal dat op als een breuk; het heeft geen zin om het uit te rekenen tot een decimaal.
2 Schrijf de reciproke van een geheel getal als een breuk. Nogmaals, de reciprook van een getal is altijd 1 ÷ (dat aantal). Schrijf voor een heel getal dat op als een breuk; het heeft geen zin om het uit te rekenen tot een decimaal. - Bijvoorbeeld, de reciprook van 2 is 1 ÷ 2 = 1/2.
Methode twee van drie:
De wederkerige van een gemengd nummer vinden
-
 1 Identificeer een gemengd nummer. Gemengde getallen zijn onderdeel geheel getal en deelfractie, zoals 24/5. Er zijn twee stappen om het omgekeerde van een gemengd getal te vinden, zoals hieronder wordt uitgelegd.
1 Identificeer een gemengd nummer. Gemengde getallen zijn onderdeel geheel getal en deelfractie, zoals 24/5. Er zijn twee stappen om het omgekeerde van een gemengd getal te vinden, zoals hieronder wordt uitgelegd. -
 2 Verander het in een onjuiste breuk. Onthoud dat het nummer 1 altijd kan worden geschreven als (nummer) / (hetzelfde nummer), en breuken met dezelfde noemer (lager getal) kunnen bij elkaar worden opgeteld. Hier is een voorbeeld met 24/5:
2 Verander het in een onjuiste breuk. Onthoud dat het nummer 1 altijd kan worden geschreven als (nummer) / (hetzelfde nummer), en breuken met dezelfde noemer (lager getal) kunnen bij elkaar worden opgeteld. Hier is een voorbeeld met 24/5: - 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
-
 3 Draai de breuk. Zodra het nummer volledig als een breuk is geschreven, kun je het omgekeerde vinden zoals je zou doen met elke breuk: door het om te draaien.
3 Draai de breuk. Zodra het nummer volledig als een breuk is geschreven, kun je het omgekeerde vinden zoals je zou doen met elke breuk: door het om te draaien. - In het bovenstaande voorbeeld, de omgekeerde van 14/5 is 5/14.
Methode drie van drie:
De wederkerige van een decimaal vinden
-
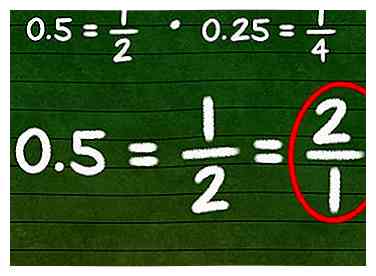 1 Verander het indien mogelijk in een breuk. Misschien herkent u enkele algemene decimale getallen die eenvoudig in breuken kunnen worden omgezet. Bijvoorbeeld 0,5 = 1/2en 0,25 = 1/4. Als je eenmaal in breukvorm bent, draai je de breuk om om het omgekeerde te vinden.
1 Verander het indien mogelijk in een breuk. Misschien herkent u enkele algemene decimale getallen die eenvoudig in breuken kunnen worden omgezet. Bijvoorbeeld 0,5 = 1/2en 0,25 = 1/4. Als je eenmaal in breukvorm bent, draai je de breuk om om het omgekeerde te vinden. - Bijvoorbeeld, de reciproke van 0,5 is 2/1 = 2.
-
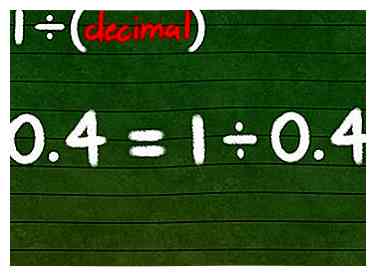 2 Schrijf een verdeeldheidsprobleem op. Als u dit niet in een breuk kunt veranderen, berekent u het omgekeerde van dat getal als een deelprobleem: 1 ÷ (het decimaalteken). U kunt een rekenmachine gebruiken om dit op te lossen, of doorgaan naar de volgende stap om het met de hand op te lossen.
2 Schrijf een verdeeldheidsprobleem op. Als u dit niet in een breuk kunt veranderen, berekent u het omgekeerde van dat getal als een deelprobleem: 1 ÷ (het decimaalteken). U kunt een rekenmachine gebruiken om dit op te lossen, of doorgaan naar de volgende stap om het met de hand op te lossen. - U kunt bijvoorbeeld de reciproke waarde van 0,4 vinden door 1 ÷ 0,4 te berekenen.
-
 3 Wijzig het delingprobleem om hele getallen te gebruiken. De eerste stap om decimalen te verdelen is om de komma te verplaatsen totdat alle betrokken getallen hele getallen zijn. Zolang u de decimale punt hetzelfde aantal spaties verplaatst voor beide getallen, krijgt u het juiste antwoord.
3 Wijzig het delingprobleem om hele getallen te gebruiken. De eerste stap om decimalen te verdelen is om de komma te verplaatsen totdat alle betrokken getallen hele getallen zijn. Zolang u de decimale punt hetzelfde aantal spaties verplaatst voor beide getallen, krijgt u het juiste antwoord. - U kunt bijvoorbeeld 1 ÷ 0,4 nemen en dit herschrijven als 10 ÷ 4. In dit geval verplaatst u elke plaats achter de komma naar rechts, wat hetzelfde is als elk getal met tien vermenigvuldigen.
-
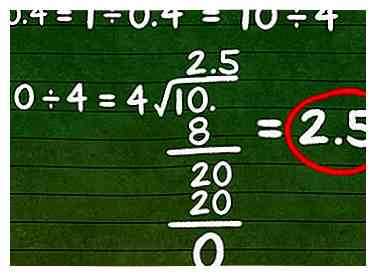 4 Los het probleem op met behulp van long-division. Gebruik langeafstandstechnieken om het omgekeerde te berekenen. Als je het voor 10 ÷ 4 berekent, krijg je het antwoord 2.5, de reciproke van 0.4.
4 Los het probleem op met behulp van long-division. Gebruik langeafstandstechnieken om het omgekeerde te berekenen. Als je het voor 10 ÷ 4 berekent, krijg je het antwoord 2.5, de reciproke van 0.4.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
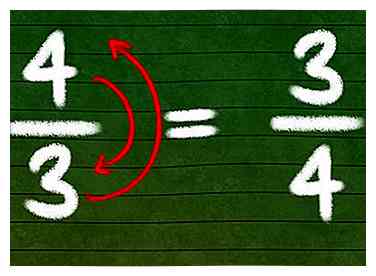 1 Vind de reciproque van een breuk door deze om te draaien. De definitie van "wederzijds" is eenvoudig. Om het omgekeerde van een willekeurig getal te vinden, berekent u gewoon "1 ÷ (dat getal)." Voor een fractie is het omgekeerde slechts een ander deel, met de cijfers omgekeerd (omgekeerd).[1]
1 Vind de reciproque van een breuk door deze om te draaien. De definitie van "wederzijds" is eenvoudig. Om het omgekeerde van een willekeurig getal te vinden, berekent u gewoon "1 ÷ (dat getal)." Voor een fractie is het omgekeerde slechts een ander deel, met de cijfers omgekeerd (omgekeerd).[1]  2 Schrijf de reciproke van een geheel getal als een breuk. Nogmaals, de reciprook van een getal is altijd 1 ÷ (dat aantal). Schrijf voor een heel getal dat op als een breuk; het heeft geen zin om het uit te rekenen tot een decimaal.
2 Schrijf de reciproke van een geheel getal als een breuk. Nogmaals, de reciprook van een getal is altijd 1 ÷ (dat aantal). Schrijf voor een heel getal dat op als een breuk; het heeft geen zin om het uit te rekenen tot een decimaal.  1 Identificeer een gemengd nummer. Gemengde getallen zijn onderdeel geheel getal en deelfractie, zoals 24/5. Er zijn twee stappen om het omgekeerde van een gemengd getal te vinden, zoals hieronder wordt uitgelegd.
1 Identificeer een gemengd nummer. Gemengde getallen zijn onderdeel geheel getal en deelfractie, zoals 24/5. Er zijn twee stappen om het omgekeerde van een gemengd getal te vinden, zoals hieronder wordt uitgelegd.  2 Verander het in een onjuiste breuk. Onthoud dat het nummer 1 altijd kan worden geschreven als (nummer) / (hetzelfde nummer), en breuken met dezelfde noemer (lager getal) kunnen bij elkaar worden opgeteld. Hier is een voorbeeld met 24/5:
2 Verander het in een onjuiste breuk. Onthoud dat het nummer 1 altijd kan worden geschreven als (nummer) / (hetzelfde nummer), en breuken met dezelfde noemer (lager getal) kunnen bij elkaar worden opgeteld. Hier is een voorbeeld met 24/5:  3 Draai de breuk. Zodra het nummer volledig als een breuk is geschreven, kun je het omgekeerde vinden zoals je zou doen met elke breuk: door het om te draaien.
3 Draai de breuk. Zodra het nummer volledig als een breuk is geschreven, kun je het omgekeerde vinden zoals je zou doen met elke breuk: door het om te draaien. 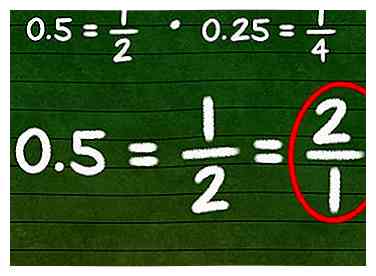 1 Verander het indien mogelijk in een breuk. Misschien herkent u enkele algemene decimale getallen die eenvoudig in breuken kunnen worden omgezet. Bijvoorbeeld 0,5 = 1/2en 0,25 = 1/4. Als je eenmaal in breukvorm bent, draai je de breuk om om het omgekeerde te vinden.
1 Verander het indien mogelijk in een breuk. Misschien herkent u enkele algemene decimale getallen die eenvoudig in breuken kunnen worden omgezet. Bijvoorbeeld 0,5 = 1/2en 0,25 = 1/4. Als je eenmaal in breukvorm bent, draai je de breuk om om het omgekeerde te vinden. 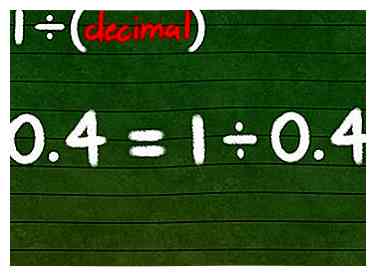 2 Schrijf een verdeeldheidsprobleem op. Als u dit niet in een breuk kunt veranderen, berekent u het omgekeerde van dat getal als een deelprobleem: 1 ÷ (het decimaalteken). U kunt een rekenmachine gebruiken om dit op te lossen, of doorgaan naar de volgende stap om het met de hand op te lossen.
2 Schrijf een verdeeldheidsprobleem op. Als u dit niet in een breuk kunt veranderen, berekent u het omgekeerde van dat getal als een deelprobleem: 1 ÷ (het decimaalteken). U kunt een rekenmachine gebruiken om dit op te lossen, of doorgaan naar de volgende stap om het met de hand op te lossen.  3 Wijzig het delingprobleem om hele getallen te gebruiken. De eerste stap om decimalen te verdelen is om de komma te verplaatsen totdat alle betrokken getallen hele getallen zijn. Zolang u de decimale punt hetzelfde aantal spaties verplaatst voor beide getallen, krijgt u het juiste antwoord.
3 Wijzig het delingprobleem om hele getallen te gebruiken. De eerste stap om decimalen te verdelen is om de komma te verplaatsen totdat alle betrokken getallen hele getallen zijn. Zolang u de decimale punt hetzelfde aantal spaties verplaatst voor beide getallen, krijgt u het juiste antwoord. 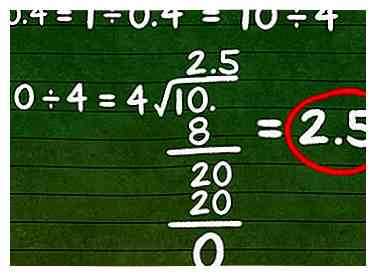 4 Los het probleem op met behulp van long-division. Gebruik langeafstandstechnieken om het omgekeerde te berekenen. Als je het voor 10 ÷ 4 berekent, krijg je het antwoord 2.5, de reciproke van 0.4.
4 Los het probleem op met behulp van long-division. Gebruik langeafstandstechnieken om het omgekeerde te berekenen. Als je het voor 10 ÷ 4 berekent, krijg je het antwoord 2.5, de reciproke van 0.4.