Je kunt vierkantswortels vermenigvuldigen, een soort radicale expressie, net zoals je hele getallen zou kunnen vermenigvuldigen. Soms hebben vierkantswortels coëfficiënten (een geheel getal voor het radicale teken), maar dit voegt alleen een stap toe aan de vermenigvuldiging en verandert het proces niet. Het lastigste deel van het vermenigvuldigen van vierkantswortels is het vereenvoudigen van de expressie om je uiteindelijke antwoord te bereiken, maar zelfs deze stap is eenvoudig als je je perfecte vierkanten kent.
Methode één van de twee:
Multiplying Square Roots zonder coëfficiënten
-
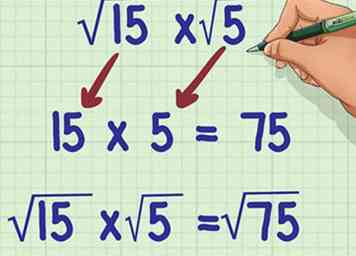 1 Vermenigvuldig de radicands. Een radicand is een getal onder het radicale teken.[1] Om vermenigvuldigingen te vermenigvuldigen, vermenigvuldigt u de cijfers alsof ze hele getallen zijn. Zorg ervoor dat het product onder één radicaal teken blijft.[2]
1 Vermenigvuldig de radicands. Een radicand is een getal onder het radicale teken.[1] Om vermenigvuldigingen te vermenigvuldigen, vermenigvuldigt u de cijfers alsof ze hele getallen zijn. Zorg ervoor dat het product onder één radicaal teken blijft.[2] - Bijvoorbeeld als u aan het rekenen bent , zou je berekenen . Zo, .
-
 2 Verbeter eventuele perfecte vierkanten in het radicand. Om dit te doen, kijk of een perfect vierkant een factor is van het radicand.[3] Als je een perfect vierkant niet kunt wegflassen, is je antwoord al vereenvoudigd en hoef je niets verder te doen.
2 Verbeter eventuele perfecte vierkanten in het radicand. Om dit te doen, kijk of een perfect vierkant een factor is van het radicand.[3] Als je een perfect vierkant niet kunt wegflassen, is je antwoord al vereenvoudigd en hoef je niets verder te doen. - Een perfect vierkant is het resultaat van het alleen vermenigvuldigen van een geheel getal (een positief of een negatief geheel getal).[4] 25 is bijvoorbeeld een perfect vierkant, omdat .
- Bijvoorbeeld, kan worden ingecalculeerd om het perfecte vierkant 25 eruit te trekken:
=
-
 3 Plaats de vierkantswortel van het perfecte vierkant voor het radicale teken. Houd de andere factor onder het radicale teken. Dit geeft je een vereenvoudigde uitdrukking.
3 Plaats de vierkantswortel van het perfecte vierkant voor het radicale teken. Houd de andere factor onder het radicale teken. Dit geeft je een vereenvoudigde uitdrukking. - Bijvoorbeeld, kan worden beschouwd als , dus je zou de vierkantswortel van 25 eruit halen (wat 5 is):
=
=
- Bijvoorbeeld, kan worden beschouwd als , dus je zou de vierkantswortel van 25 eruit halen (wat 5 is):
-
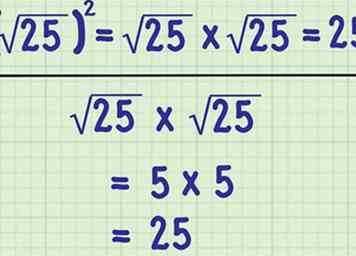 4 Vierkant een vierkantswortel. In sommige gevallen moet u een vierkantswortel alleen vermenigvuldigen. Een getal uitlijnen en de vierkantswortel van een getal nemen zijn tegengestelde bewerkingen; dus maken ze elkaar ongedaan. Het resultaat van het kwadraat van een vierkantswortel is dan eenvoudigweg het getal onder het radicale teken.[5]
4 Vierkant een vierkantswortel. In sommige gevallen moet u een vierkantswortel alleen vermenigvuldigen. Een getal uitlijnen en de vierkantswortel van een getal nemen zijn tegengestelde bewerkingen; dus maken ze elkaar ongedaan. Het resultaat van het kwadraat van een vierkantswortel is dan eenvoudigweg het getal onder het radicale teken.[5] - Bijvoorbeeld, . Je krijgt dat resultaat omdat .
Methode twee van twee:
Multiplying Square Roots met coëfficiënten
-
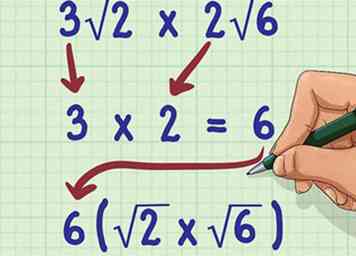 1 Vermenigvuldig de coëfficiënten. Een coëfficiënt is een getal voor het radicale teken. Om dit te doen, negeer gewoon het radicale teken en radicand, en vermenigvuldig de twee hele getallen. Plaats hun product voor het eerste radicale teken.
1 Vermenigvuldig de coëfficiënten. Een coëfficiënt is een getal voor het radicale teken. Om dit te doen, negeer gewoon het radicale teken en radicand, en vermenigvuldig de twee hele getallen. Plaats hun product voor het eerste radicale teken. - Let op positieve en negatieve tekens bij het vermenigvuldigen van coëfficiënten. Vergeet niet dat een negatieve tijd een positieve is een negatieve, en een negatieve keer een negatieve is een positieve.
- Bijvoorbeeld als u aan het rekenen bent , zou je eerst berekenen . Dus nu is je probleem .
-
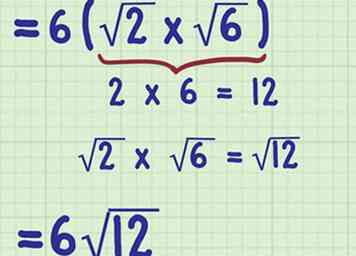 2 Vermenigvuldig de radicands. Om dit te doen, vermenigvuldigt u de cijfers alsof ze hele getallen zijn. Zorg ervoor dat het product onder het radicale teken blijft.
2 Vermenigvuldig de radicands. Om dit te doen, vermenigvuldigt u de cijfers alsof ze hele getallen zijn. Zorg ervoor dat het product onder het radicale teken blijft. - Bijvoorbeeld, als het probleem nu is , om het product van de radicanden te vinden, zou je het berekenen , dus . Het probleem wordt nu .
-
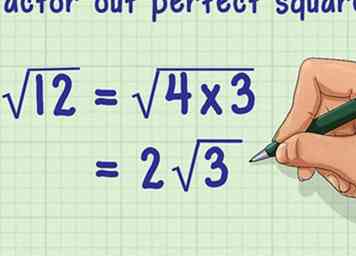 3 Verbeter eventuele perfecte vierkanten in de radicand, indien mogelijk. U moet dit doen om uw antwoord te vereenvoudigen.[6] Als u geen perfect vierkant kunt trekken, is uw antwoord al vereenvoudigd en kunt u deze stap overslaan.
3 Verbeter eventuele perfecte vierkanten in de radicand, indien mogelijk. U moet dit doen om uw antwoord te vereenvoudigen.[6] Als u geen perfect vierkant kunt trekken, is uw antwoord al vereenvoudigd en kunt u deze stap overslaan. - Een perfect vierkant is het resultaat van het alleen vermenigvuldigen van een geheel getal (een positief of een negatief geheel getal).[7] 4 is bijvoorbeeld een perfect vierkant, omdat .
- Bijvoorbeeld, kan worden ingecalculeerd om het perfecte vierkant 4 eruit te halen:
=
-
 4 Vermenigvuldig de vierkantswortel van het perfecte vierkant met de coëfficiënt. Houd de andere factor onder de radicand. Dit geeft je een vereenvoudigde uitdrukking.
4 Vermenigvuldig de vierkantswortel van het perfecte vierkant met de coëfficiënt. Houd de andere factor onder de radicand. Dit geeft je een vereenvoudigde uitdrukking. - Bijvoorbeeld, kan worden beschouwd als , dus je zou de vierkantswortel van 4 (dat is 2) eruit halen en het met 6 vermenigvuldigen:
=
=
=
- Bijvoorbeeld, kan worden beschouwd als , dus je zou de vierkantswortel van 4 (dat is 2) eruit halen en het met 6 vermenigvuldigen:
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
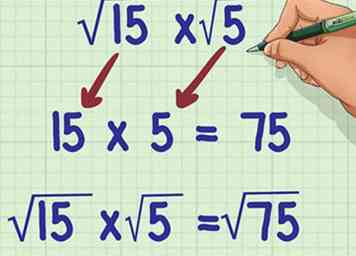 1 Vermenigvuldig de radicands. Een radicand is een getal onder het radicale teken.[1] Om vermenigvuldigingen te vermenigvuldigen, vermenigvuldigt u de cijfers alsof ze hele getallen zijn. Zorg ervoor dat het product onder één radicaal teken blijft.[2]
1 Vermenigvuldig de radicands. Een radicand is een getal onder het radicale teken.[1] Om vermenigvuldigingen te vermenigvuldigen, vermenigvuldigt u de cijfers alsof ze hele getallen zijn. Zorg ervoor dat het product onder één radicaal teken blijft.[2]  2 Verbeter eventuele perfecte vierkanten in het radicand. Om dit te doen, kijk of een perfect vierkant een factor is van het radicand.[3] Als je een perfect vierkant niet kunt wegflassen, is je antwoord al vereenvoudigd en hoef je niets verder te doen.
2 Verbeter eventuele perfecte vierkanten in het radicand. Om dit te doen, kijk of een perfect vierkant een factor is van het radicand.[3] Als je een perfect vierkant niet kunt wegflassen, is je antwoord al vereenvoudigd en hoef je niets verder te doen.  3 Plaats de vierkantswortel van het perfecte vierkant voor het radicale teken. Houd de andere factor onder het radicale teken. Dit geeft je een vereenvoudigde uitdrukking.
3 Plaats de vierkantswortel van het perfecte vierkant voor het radicale teken. Houd de andere factor onder het radicale teken. Dit geeft je een vereenvoudigde uitdrukking. 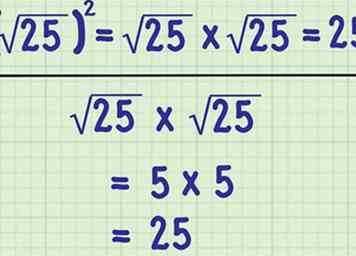 4 Vierkant een vierkantswortel. In sommige gevallen moet u een vierkantswortel alleen vermenigvuldigen. Een getal uitlijnen en de vierkantswortel van een getal nemen zijn tegengestelde bewerkingen; dus maken ze elkaar ongedaan. Het resultaat van het kwadraat van een vierkantswortel is dan eenvoudigweg het getal onder het radicale teken.[5]
4 Vierkant een vierkantswortel. In sommige gevallen moet u een vierkantswortel alleen vermenigvuldigen. Een getal uitlijnen en de vierkantswortel van een getal nemen zijn tegengestelde bewerkingen; dus maken ze elkaar ongedaan. Het resultaat van het kwadraat van een vierkantswortel is dan eenvoudigweg het getal onder het radicale teken.[5] 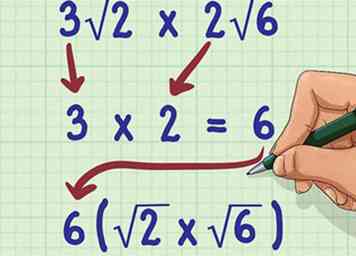 1 Vermenigvuldig de coëfficiënten. Een coëfficiënt is een getal voor het radicale teken. Om dit te doen, negeer gewoon het radicale teken en radicand, en vermenigvuldig de twee hele getallen. Plaats hun product voor het eerste radicale teken.
1 Vermenigvuldig de coëfficiënten. Een coëfficiënt is een getal voor het radicale teken. Om dit te doen, negeer gewoon het radicale teken en radicand, en vermenigvuldig de twee hele getallen. Plaats hun product voor het eerste radicale teken. 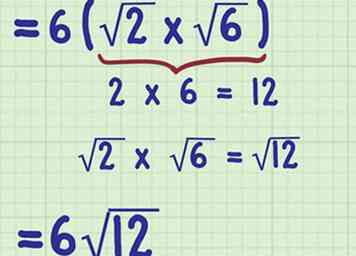 2 Vermenigvuldig de radicands. Om dit te doen, vermenigvuldigt u de cijfers alsof ze hele getallen zijn. Zorg ervoor dat het product onder het radicale teken blijft.
2 Vermenigvuldig de radicands. Om dit te doen, vermenigvuldigt u de cijfers alsof ze hele getallen zijn. Zorg ervoor dat het product onder het radicale teken blijft. 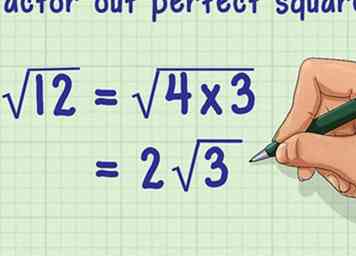 3 Verbeter eventuele perfecte vierkanten in de radicand, indien mogelijk. U moet dit doen om uw antwoord te vereenvoudigen.[6] Als u geen perfect vierkant kunt trekken, is uw antwoord al vereenvoudigd en kunt u deze stap overslaan.
3 Verbeter eventuele perfecte vierkanten in de radicand, indien mogelijk. U moet dit doen om uw antwoord te vereenvoudigen.[6] Als u geen perfect vierkant kunt trekken, is uw antwoord al vereenvoudigd en kunt u deze stap overslaan.  4 Vermenigvuldig de vierkantswortel van het perfecte vierkant met de coëfficiënt. Houd de andere factor onder de radicand. Dit geeft je een vereenvoudigde uitdrukking.
4 Vermenigvuldig de vierkantswortel van het perfecte vierkant met de coëfficiënt. Houd de andere factor onder de radicand. Dit geeft je een vereenvoudigde uitdrukking.