In tegenstelling tot een rechte lijn verandert de helling van een curve voortdurend terwijl u langs de grafiek beweegt. Calculus introduceert studenten aan het idee dat elk punt in deze grafiek kan worden beschreven met een helling of een "momentane veranderingssnelheid". De raaklijn is een rechte lijn met die helling en loopt door dat exacte punt in de grafiek. Om de vergelijking voor de tangens te vinden, moet u weten hoe u de afgeleide van de oorspronkelijke vergelijking moet nemen.
Methode één van de twee:
De vergelijking van een raaklijn vinden
-
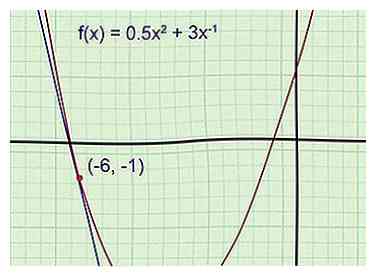 1 Teken de functie en de raaklijn (aanbevolen). Een grafiek maakt het gemakkelijker om het probleem te volgen en te controleren of het antwoord klopt. Schets de functie op een stuk ruitjespapier, gebruik indien nodig een grafische rekenmachine als referentie. Schets de raaklijn door het gegeven punt. (Denk eraan, de raaklijn loopt door dat punt en heeft op dat punt dezelfde helling als de grafiek.)
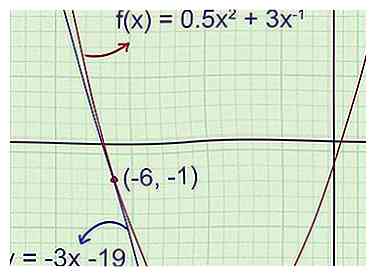
1 Teken de functie en de raaklijn (aanbevolen). Een grafiek maakt het gemakkelijker om het probleem te volgen en te controleren of het antwoord klopt. Schets de functie op een stuk ruitjespapier, gebruik indien nodig een grafische rekenmachine als referentie. Schets de raaklijn door het gegeven punt. (Denk eraan, de raaklijn loopt door dat punt en heeft op dat punt dezelfde helling als de grafiek.) - Voorbeeld 1: Schets de grafiek van de parabool . Trek de tangens door het punt (-6, -1).
Je kent de vergelijking van de raaklijn nog niet, maar je kunt al zien dat de helling negatief is, en dat het y-snijpunt negatief is (ruim onder de paraboolvertex met y-waarde -5,5). Als je laatste antwoord niet overeenkomt met deze details, weet je dat je je werk op fouten moet controleren.
- Voorbeeld 1: Schets de grafiek van de parabool . Trek de tangens door het punt (-6, -1).
-
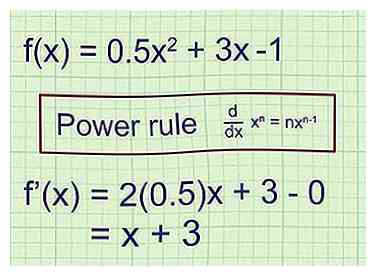 2 Neem de eerste afgeleide om de vergelijking voor de te vinden helling van de raaklijn. Voor functie f (x) vertegenwoordigt de eerste afgeleide f '(x) de vergelijking voor de helling van de raaklijn op elk punt op f (x). Er zijn veel manieren om derivaten te nemen. Hier is een eenvoudig voorbeeld met behulp van de machtsregel:[1]
2 Neem de eerste afgeleide om de vergelijking voor de te vinden helling van de raaklijn. Voor functie f (x) vertegenwoordigt de eerste afgeleide f '(x) de vergelijking voor de helling van de raaklijn op elk punt op f (x). Er zijn veel manieren om derivaten te nemen. Hier is een eenvoudig voorbeeld met behulp van de machtsregel:[1] - Voorbeeld 1 (vervolg): De grafiek wordt beschreven door de functie .
Denk aan de machtsregel bij het nemen van derivaten: .
De eerste afgeleide van de functie = f '(x) = (2) (0,5) x + 3 - 0.
f '(x) = x + 3. Steek elke waarde a voor x in deze vergelijking en het resultaat is de helling van de lijn die raakt aan f (x) op het punt waar x = a is.
- Voorbeeld 1 (vervolg): De grafiek wordt beschreven door de functie .
-
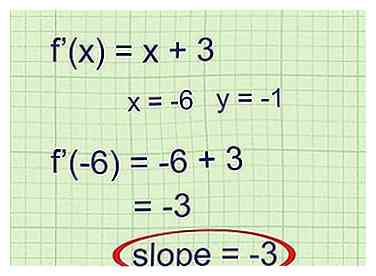 3 Voer de x-waarde in van het punt dat u aan het onderzoeken bent. Lees het probleem om de coördinaten te vinden van het punt waarvoor u de raaklijn vindt. Voer de x-coördinaat van dit punt in f (x) in. De uitvoer is de helling van de raaklijn op dit punt.
3 Voer de x-waarde in van het punt dat u aan het onderzoeken bent. Lees het probleem om de coördinaten te vinden van het punt waarvoor u de raaklijn vindt. Voer de x-coördinaat van dit punt in f (x) in. De uitvoer is de helling van de raaklijn op dit punt. - Voorbeeld 1 (vervolg): Het punt dat in het probleem wordt genoemd is (-6, -1). Gebruik de x-coördinaat -6 als de invoer voor f '(x):
f '(- 6) = -6 + 3 = -3
De helling van de raaklijn is -3.
- Voorbeeld 1 (vervolg): Het punt dat in het probleem wordt genoemd is (-6, -1). Gebruik de x-coördinaat -6 als de invoer voor f '(x):
-
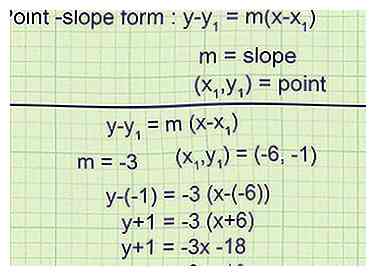 4 Noteer de vergelijking van de raaklijn in punt-hellingsvorm. De punt-hellingsvorm van een lineaire vergelijking is , waar m is de helling en is een punt op de lijn.[2] Je hebt nu alle informatie die je nodig hebt om de vergelijking van de raaklijn in dit formulier te schrijven.
4 Noteer de vergelijking van de raaklijn in punt-hellingsvorm. De punt-hellingsvorm van een lineaire vergelijking is , waar m is de helling en is een punt op de lijn.[2] Je hebt nu alle informatie die je nodig hebt om de vergelijking van de raaklijn in dit formulier te schrijven. - Voorbeeld 1 (vervolg):
De helling van de lijn is -3, dus
De raaklijn loopt door (-6, -1), dus de laatste vergelijking is
Simplify to
- Voorbeeld 1 (vervolg):
-
 5 Bevestig de vergelijking in uw grafiek. Als je een grafische rekenmachine hebt, teken dan de oorspronkelijke functie en de raaklijn om te controleren of je het juiste antwoord hebt. Als u op papier werkt, raadpleegt u uw eerdere grafiek om ervoor te zorgen dat uw antwoord geen flagrante fouten bevat.
5 Bevestig de vergelijking in uw grafiek. Als je een grafische rekenmachine hebt, teken dan de oorspronkelijke functie en de raaklijn om te controleren of je het juiste antwoord hebt. Als u op papier werkt, raadpleegt u uw eerdere grafiek om ervoor te zorgen dat uw antwoord geen flagrante fouten bevat. - Voorbeeld 1 (vervolg): De eerste schets toonde aan dat de helling van de raaklijn negatief was en dat het y-snijpunt ruim onder -5,5 lag. De raaklijnvergelijking die we hebben gevonden is y = -3x - 19 in de hellingsinterceptievorm, wat betekent dat -3 de helling is en -19 het y-snijpunt is. Beide attributen komen overeen met de eerste voorspellingen.
-
 6 Probeer een moeilijker probleem. Hier is opnieuw een overzicht van het hele proces. Deze keer is het doel om de lijn tangent te vinden bij x = 2:
6 Probeer een moeilijker probleem. Hier is opnieuw een overzicht van het hele proces. Deze keer is het doel om de lijn tangent te vinden bij x = 2: - Met behulp van de power rule, de eerste afgeleide . Deze functie vertelt ons de helling van de tangens.
- Aangezien x = 2, vind . Dit is de helling op x = 2.
- Merk op dat we deze keer geen punt hebben, alleen een x-coördinaat. Om de y-coördinaat te vinden, steekt u x = 2 in de oorspronkelijke functie: . Het punt is (2,27).
- Schrijf de vergelijking van de raaklijn in punt-hellingsvorm:
Vereenvoudig indien nodig naar y = 25x - 23.
Methode twee van twee:
Verwante problemen oplossen
-
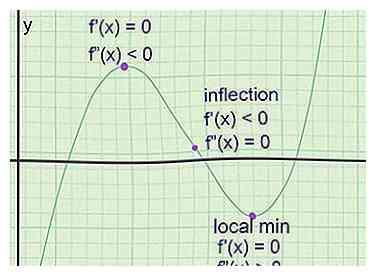 1 Zoek de extreme punten in een grafiek. Dit zijn punten waar de grafiek een lokaal maximum bereikt (een punt dat hoger is dan de punten aan weerszijden) of lokaal minimum (lager dan de punten aan weerszijden). De raaklijn heeft altijd een helling van 0 op deze punten (een horizontale lijn), maar een helling op nul garandeert geen extreem punt. Zo kunt u ze vinden:[3]
1 Zoek de extreme punten in een grafiek. Dit zijn punten waar de grafiek een lokaal maximum bereikt (een punt dat hoger is dan de punten aan weerszijden) of lokaal minimum (lager dan de punten aan weerszijden). De raaklijn heeft altijd een helling van 0 op deze punten (een horizontale lijn), maar een helling op nul garandeert geen extreem punt. Zo kunt u ze vinden:[3] - Neem de eerste afgeleide van de functie om f '(x) te krijgen, de vergelijking voor de helling van de raaklijn.
- Los op voor f '(x) = 0 om te vinden mogelijk extreme punten.
- Neem de tweede afgeleide om f "(x) te krijgen, de vergelijking die aangeeft hoe snel de helling van de raaklijn verandert.
- Sluit voor elk mogelijk extreem punt de x-coördinaat aan een in f "(x). Als f" (a) positief is, is er een lokaal minimum op een. Als f "(a) negatief is, is er een lokaal maximum.Als f" (a) 0 is, is er een buigpunt, geen extreem punt.
- Als er een maximum of minimum is op een, zoek f (a) om de y-coördinaat te krijgen.
-
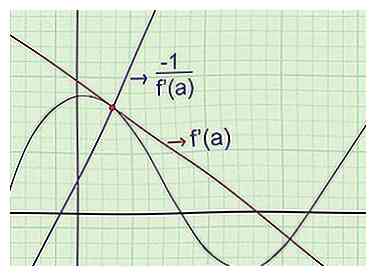 2 Zoek de vergelijking van de normale. Het "normale" van een curve op een bepaald punt gaat door dat punt, maar heeft een helling loodrecht op een raaklijn. Om de vergelijking voor de normaal te vinden, profiteer van het feit dat (helling van de tangens) (helling van normaal) = -1, wanneer ze allebei hetzelfde punt in de grafiek passeren.[4] Met andere woorden:
2 Zoek de vergelijking van de normale. Het "normale" van een curve op een bepaald punt gaat door dat punt, maar heeft een helling loodrecht op een raaklijn. Om de vergelijking voor de normaal te vinden, profiteer van het feit dat (helling van de tangens) (helling van normaal) = -1, wanneer ze allebei hetzelfde punt in de grafiek passeren.[4] Met andere woorden: - Zoek f '(x), de helling van de raaklijn.
- Als het punt op x = is een, vind f '(a) om de helling van de raaklijn op dat punt te vinden.
- Berekenen om de helling van de normaal te vinden.
- Schrijf de normale vergelijking in hellingspuntvorm.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Teken de functie en de raaklijn (aanbevolen). Een grafiek maakt het gemakkelijker om het probleem te volgen en te controleren of het antwoord klopt. Schets de functie op een stuk ruitjespapier, gebruik indien nodig een grafische rekenmachine als referentie. Schets de raaklijn door het gegeven punt. (Denk eraan, de raaklijn loopt door dat punt en heeft op dat punt dezelfde helling als de grafiek.)
1 Teken de functie en de raaklijn (aanbevolen). Een grafiek maakt het gemakkelijker om het probleem te volgen en te controleren of het antwoord klopt. Schets de functie op een stuk ruitjespapier, gebruik indien nodig een grafische rekenmachine als referentie. Schets de raaklijn door het gegeven punt. (Denk eraan, de raaklijn loopt door dat punt en heeft op dat punt dezelfde helling als de grafiek.) 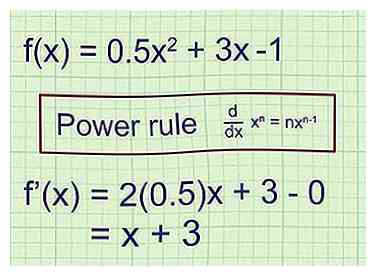 2 Neem de eerste afgeleide om de vergelijking voor de te vinden helling van de raaklijn. Voor functie f (x) vertegenwoordigt de eerste afgeleide f '(x) de vergelijking voor de helling van de raaklijn op elk punt op f (x). Er zijn veel manieren om derivaten te nemen. Hier is een eenvoudig voorbeeld met behulp van de machtsregel:[1]
2 Neem de eerste afgeleide om de vergelijking voor de te vinden helling van de raaklijn. Voor functie f (x) vertegenwoordigt de eerste afgeleide f '(x) de vergelijking voor de helling van de raaklijn op elk punt op f (x). Er zijn veel manieren om derivaten te nemen. Hier is een eenvoudig voorbeeld met behulp van de machtsregel:[1] 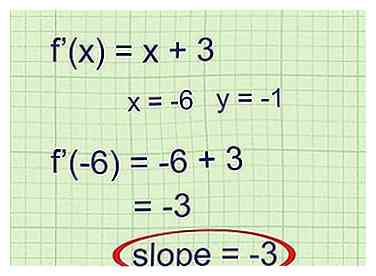 3 Voer de x-waarde in van het punt dat u aan het onderzoeken bent. Lees het probleem om de coördinaten te vinden van het punt waarvoor u de raaklijn vindt. Voer de x-coördinaat van dit punt in f (x) in. De uitvoer is de helling van de raaklijn op dit punt.
3 Voer de x-waarde in van het punt dat u aan het onderzoeken bent. Lees het probleem om de coördinaten te vinden van het punt waarvoor u de raaklijn vindt. Voer de x-coördinaat van dit punt in f (x) in. De uitvoer is de helling van de raaklijn op dit punt. 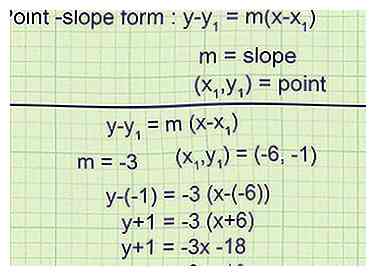 4 Noteer de vergelijking van de raaklijn in punt-hellingsvorm. De punt-hellingsvorm van een lineaire vergelijking is
4 Noteer de vergelijking van de raaklijn in punt-hellingsvorm. De punt-hellingsvorm van een lineaire vergelijking is  5 Bevestig de vergelijking in uw grafiek. Als je een grafische rekenmachine hebt, teken dan de oorspronkelijke functie en de raaklijn om te controleren of je het juiste antwoord hebt. Als u op papier werkt, raadpleegt u uw eerdere grafiek om ervoor te zorgen dat uw antwoord geen flagrante fouten bevat.
5 Bevestig de vergelijking in uw grafiek. Als je een grafische rekenmachine hebt, teken dan de oorspronkelijke functie en de raaklijn om te controleren of je het juiste antwoord hebt. Als u op papier werkt, raadpleegt u uw eerdere grafiek om ervoor te zorgen dat uw antwoord geen flagrante fouten bevat.  6 Probeer een moeilijker probleem. Hier is opnieuw een overzicht van het hele proces. Deze keer is het doel om de lijn tangent te vinden
6 Probeer een moeilijker probleem. Hier is opnieuw een overzicht van het hele proces. Deze keer is het doel om de lijn tangent te vinden  1 Zoek de extreme punten in een grafiek. Dit zijn punten waar de grafiek een lokaal maximum bereikt (een punt dat hoger is dan de punten aan weerszijden) of lokaal minimum (lager dan de punten aan weerszijden). De raaklijn heeft altijd een helling van 0 op deze punten (een horizontale lijn), maar een helling op nul garandeert geen extreem punt. Zo kunt u ze vinden:[3]
1 Zoek de extreme punten in een grafiek. Dit zijn punten waar de grafiek een lokaal maximum bereikt (een punt dat hoger is dan de punten aan weerszijden) of lokaal minimum (lager dan de punten aan weerszijden). De raaklijn heeft altijd een helling van 0 op deze punten (een horizontale lijn), maar een helling op nul garandeert geen extreem punt. Zo kunt u ze vinden:[3]  2 Zoek de vergelijking van de normale. Het "normale" van een curve op een bepaald punt gaat door dat punt, maar heeft een helling loodrecht op een raaklijn. Om de vergelijking voor de normaal te vinden, profiteer van het feit dat (helling van de tangens) (helling van normaal) = -1, wanneer ze allebei hetzelfde punt in de grafiek passeren.[4] Met andere woorden:
2 Zoek de vergelijking van de normale. Het "normale" van een curve op een bepaald punt gaat door dat punt, maar heeft een helling loodrecht op een raaklijn. Om de vergelijking voor de normaal te vinden, profiteer van het feit dat (helling van de tangens) (helling van normaal) = -1, wanneer ze allebei hetzelfde punt in de grafiek passeren.[4] Met andere woorden: