Het vinden van hoeveel factoren er in een getal zitten, is net zo gemakkelijk een 1 2 3 als je weet hoe je het moet doen. Maar voor grotere aantallen kunt u niet één voor één tellen. Dit is een leuke truc om te achterhalen hoeveel factoren zich in een geheel getal bevinden.
Stappen
-
 1 Identificeer het nummer. Elk nummer ter wereld, maar het is het beste om te beginnen met de eenvoudigere.
1 Identificeer het nummer. Elk nummer ter wereld, maar het is het beste om te beginnen met de eenvoudigere. - Neem bijvoorbeeld 72, maar het getal kan worden aangegeven met een variabele.
-
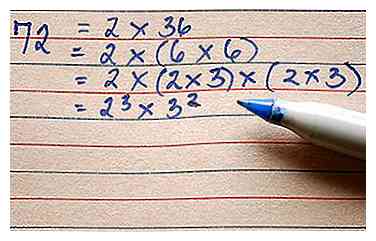 2 Bereken de Prime Factorization van het aantal. Er zijn veel methoden om dit te doen, maar meestal is de eenvoudigste manier om een factorboom te maken. Dit werkt omdat, volgens de getaltheorie, elk geheel getal (behalve -1, 0 en 1) een aantal priemgetallen heeft die, wanneer ze worden vermenigvuldigd, gelijk zullen zijn aan het aantal. Onthoud dat 0 en 1 zijn niet priemgetallen.
2 Bereken de Prime Factorization van het aantal. Er zijn veel methoden om dit te doen, maar meestal is de eenvoudigste manier om een factorboom te maken. Dit werkt omdat, volgens de getaltheorie, elk geheel getal (behalve -1, 0 en 1) een aantal priemgetallen heeft die, wanneer ze worden vermenigvuldigd, gelijk zullen zijn aan het aantal. Onthoud dat 0 en 1 zijn niet priemgetallen. - 72 moet worden ontbonden in 2 en 36, 2, 6 en 6, en tot slot, 2, 2, 3, 2, 3, wat gelijk is aan 23*32.
-
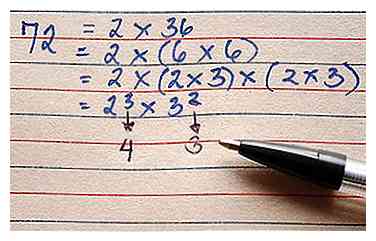 3 Neem alle exponenten en voeg er een toe aan elk van hen.
3 Neem alle exponenten en voeg er een toe aan elk van hen. - In het voorbeeld 23 en 32, de exponenten zijn 3 en 2 - het toevoegen van één aan elk maakt ze 4 en 3.
-
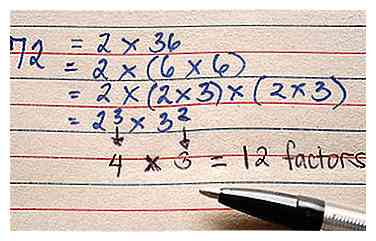 4 Vermenigvuldig de gewijzigde exponenten samen.
4 Vermenigvuldig de gewijzigde exponenten samen. - 4 x 3 = 12. Er zijn 12 factoren voor het getal 72 - 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 en 72.
Voorbeelden
7540
- 1
- Prime Factorization - 225 (29) (13). Nu, omdat x1 = x, 29, 13 en 5 hebben allemaal exponenten naar de eerste macht.
- Exponenten met één toevoegen. 3, 2, 2, 2.
- Vermenigvuldig de gewijzigde exponenten samen. Er zijn 24 factoren van het getal 7540.
15802
- 1
- Prime Factorization - 2 (7901)
- Wijzig exponenten - 2, 2
- Vermenigvuldigen. Er zijn vier factoren van het nummer 15802 - 1, 2, 7901, 15802. 7901 is een priemgetal.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Identificeer het nummer. Elk nummer ter wereld, maar het is het beste om te beginnen met de eenvoudigere.
1 Identificeer het nummer. Elk nummer ter wereld, maar het is het beste om te beginnen met de eenvoudigere. 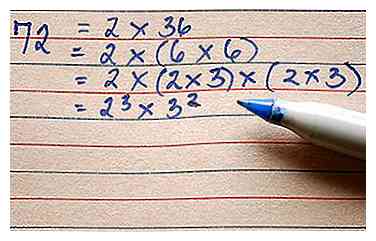 2 Bereken de Prime Factorization van het aantal. Er zijn veel methoden om dit te doen, maar meestal is de eenvoudigste manier om een factorboom te maken. Dit werkt omdat, volgens de getaltheorie, elk geheel getal (behalve -1, 0 en 1) een aantal priemgetallen heeft die, wanneer ze worden vermenigvuldigd, gelijk zullen zijn aan het aantal. Onthoud dat 0 en 1 zijn niet priemgetallen.
2 Bereken de Prime Factorization van het aantal. Er zijn veel methoden om dit te doen, maar meestal is de eenvoudigste manier om een factorboom te maken. Dit werkt omdat, volgens de getaltheorie, elk geheel getal (behalve -1, 0 en 1) een aantal priemgetallen heeft die, wanneer ze worden vermenigvuldigd, gelijk zullen zijn aan het aantal. Onthoud dat 0 en 1 zijn niet priemgetallen. 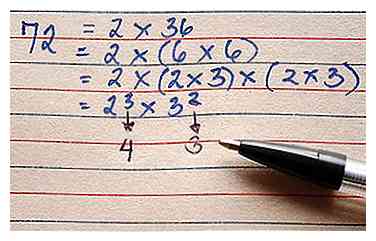 3 Neem alle exponenten en voeg er een toe aan elk van hen.
3 Neem alle exponenten en voeg er een toe aan elk van hen. 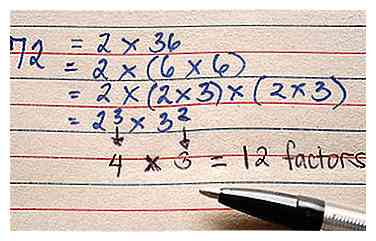 4 Vermenigvuldig de gewijzigde exponenten samen.
4 Vermenigvuldig de gewijzigde exponenten samen.