Wanneer twee variabelen direct proportioneel zijn, veranderen ze in hetzelfde tempo. De snelheid wordt weergegeven door de constante in de vergelijking . Rechtstreeks proportionele variabelen worden grafisch aangegeven door een rechte lijn die door de oorsprong van het coördinatenvlak loopt. Als u eenmaal deze basisbegrippen begrijpt, is het eenvoudig om direct proportionele variabelen te identificeren door de vergelijking van hun lijn of hun waarden te gebruiken.
Methode één van de vier:
De vergelijking van de lijn herschrijven
-
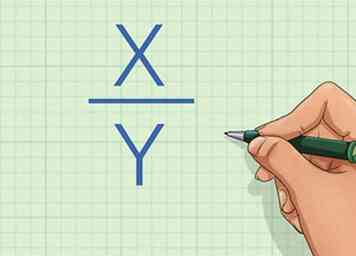 1 Begrijp de directe verhouding. Twee variabelen staan in directe verhouding als elke variabele met dezelfde snelheid verandert.[1] Met andere woorden, als veranderingen met een bepaalde factor of constante (), dan veranderingen door diezelfde constante ().
1 Begrijp de directe verhouding. Twee variabelen staan in directe verhouding als elke variabele met dezelfde snelheid verandert.[1] Met andere woorden, als veranderingen met een bepaalde factor of constante (), dan veranderingen door diezelfde constante (). -
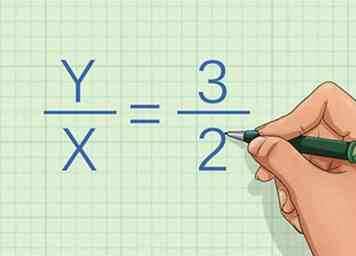 2 Noteer de vergelijking van de regel. De vergelijking heeft twee variabelen en een constante. Als u de vergelijking niet krijgt, kunt u deze methode niet gebruiken.
2 Noteer de vergelijking van de regel. De vergelijking heeft twee variabelen en een constante. Als u de vergelijking niet krijgt, kunt u deze methode niet gebruiken. - U kunt bijvoorbeeld de vergelijking krijgen .
-
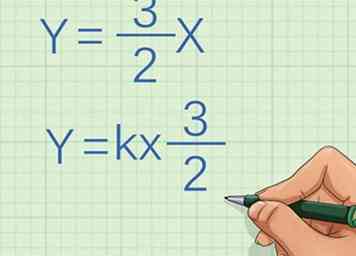 3 Herschrijf de vergelijking in de vorm van directe proportie of variatie. De vergelijking is , waar is gelijk aan de y-coördinaat van een punt op de lijn, is gelijk aan de x-coördinaat voor datzelfde punt, en is de constante of helling van de lijn. Gebruik de algebra om de vergelijking opnieuw in te delen in de vorm van . Als u de vergelijking in dit formulier niet kunt herschrijven, zijn de variabelen niet direct proportioneel. Als je kunt, bewijst het dat ze recht evenredig zijn.[2]
3 Herschrijf de vergelijking in de vorm van directe proportie of variatie. De vergelijking is , waar is gelijk aan de y-coördinaat van een punt op de lijn, is gelijk aan de x-coördinaat voor datzelfde punt, en is de constante of helling van de lijn. Gebruik de algebra om de vergelijking opnieuw in te delen in de vorm van . Als u de vergelijking in dit formulier niet kunt herschrijven, zijn de variabelen niet direct proportioneel. Als je kunt, bewijst het dat ze recht evenredig zijn.[2] - Als u bijvoorbeeld beide zijden van de vergelijking vermenigvuldigt door , de vergelijking wordt , die de vorm heeft van , met de constante zijn.
Methode twee van vier:
Een set van punten gebruiken
-
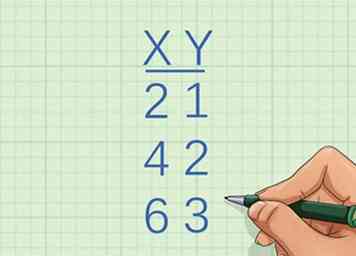 1 Identificeer de x-coördinaten van de eerste twee punten. Je zou een lijst met coördinaten moeten krijgen, of een grafiek hebben waaruit je de coördinaten van de punten kunt bepalen. Als u niet de coördinaten van punten op de lijn hebt, kunt u deze methode niet gebruiken.
1 Identificeer de x-coördinaten van de eerste twee punten. Je zou een lijst met coördinaten moeten krijgen, of een grafiek hebben waaruit je de coördinaten van de punten kunt bepalen. Als u niet de coördinaten van punten op de lijn hebt, kunt u deze methode niet gebruiken. - U kunt bijvoorbeeld de verzameling punten krijgen
- De x-coördinaat van het eerste punt is 2 en de x-coördinaat van het tweede punt is 4.
-
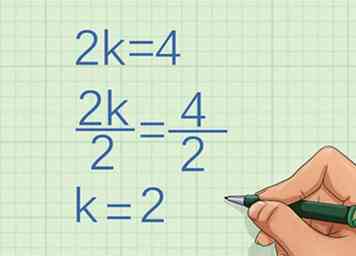 2 Bepaal de factor waarmee de variabele groeit. Hiertoe bepaalt u met welke factor of constante de eerste x-coördinaat wordt vermenigvuldigd met de tweede coördinaat.
2 Bepaal de factor waarmee de variabele groeit. Hiertoe bepaalt u met welke factor of constante de eerste x-coördinaat wordt vermenigvuldigd met de tweede coördinaat. - Als de eerste x-coördinaat bijvoorbeeld 2 is en de tweede x-coördinaat 4, moet u bepalen wat u met 2 vermenigvuldigt om 4 te krijgen:
Dus de variabele groeit met de constante 2.
- Als de eerste x-coördinaat bijvoorbeeld 2 is en de tweede x-coördinaat 4, moet u bepalen wat u met 2 vermenigvuldigt om 4 te krijgen:
-
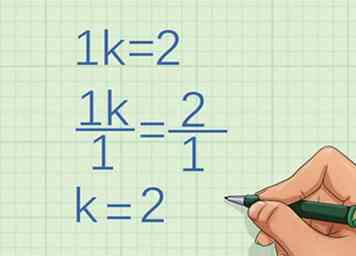 3 Bepaal de factor waarmee de variabele groeit. Gebruik dezelfde twee punten die je hebt gebruikt om de groei van te bepalen . Gebruik de algebra om de factor te bepalen waarmee de twee coördinaten variëren.
3 Bepaal de factor waarmee de variabele groeit. Gebruik dezelfde twee punten die je hebt gebruikt om de groei van te bepalen . Gebruik de algebra om de factor te bepalen waarmee de twee coördinaten variëren. - Als de eerste y-coördinaat bijvoorbeeld 1 is en de tweede y-coördinaat 2 is, moet u bepalen wat u met 1 vermenigvuldigt om 2 te krijgen:
Dus de variabele groeit met de constante 2.
- Als de eerste y-coördinaat bijvoorbeeld 1 is en de tweede y-coördinaat 2 is, moet u bepalen wat u met 1 vermenigvuldigt om 2 te krijgen:
-
 4 Vergelijk de constanten van de twee variabelen. Als en veranderd met dezelfde snelheid, of met dezelfde factor, dan zijn ze direct proportioneel.[3]
4 Vergelijk de constanten van de twee variabelen. Als en veranderd met dezelfde snelheid, of met dezelfde factor, dan zijn ze direct proportioneel.[3] - Omdat de x-coördinaten bijvoorbeeld met een factor 2 zijn gewijzigd terwijl de y-coördinaten ook met een factor 2 zijn gewijzigd, zijn de twee variabelen direct proportioneel.
Methode drie van vier:
Een grafiek gebruiken
-
 1 Let op of de lijn recht is. Als twee variabelen in verhouding zijn, is de regel die hen vertegenwoordigt recht.[4] Dit betekent dat de helling van de lijn constant is, of de vergelijking volgt .
1 Let op of de lijn recht is. Als twee variabelen in verhouding zijn, is de regel die hen vertegenwoordigt recht.[4] Dit betekent dat de helling van de lijn constant is, of de vergelijking volgt . -
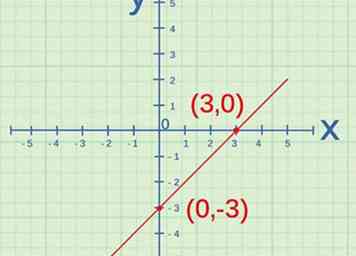 2 Bepaal het y-snijpunt. Het y-snijpunt is het punt waar de lijn de y-as kruist. Wanneer twee variabelen direct proportioneel zijn, zal hun lijn in de grafiek door de oorsprong lopen. De oorsprong is op het punt , dus het y-snijpunt van de lijn zou moeten zijn . Als dat niet het geval is, zijn de variabelen niet rechtevenredig.[5]
2 Bepaal het y-snijpunt. Het y-snijpunt is het punt waar de lijn de y-as kruist. Wanneer twee variabelen direct proportioneel zijn, zal hun lijn in de grafiek door de oorsprong lopen. De oorsprong is op het punt , dus het y-snijpunt van de lijn zou moeten zijn . Als dat niet het geval is, zijn de variabelen niet rechtevenredig.[5] - De y-as is de verticale as.
-
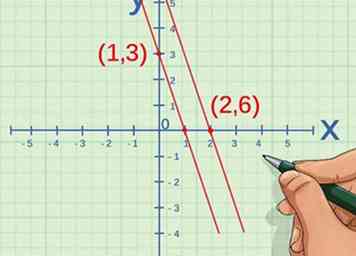 3 Zoek de coördinaten van twee punten op de lijn. Vergelijk de coördinaten met elkaar en bepaal of elke coördinaat met dezelfde factor is gewijzigd.[6] Dat wil zeggen, bepalen of de constante () is hetzelfde voor beide en waarden.
3 Zoek de coördinaten van twee punten op de lijn. Vergelijk de coördinaten met elkaar en bepaal of elke coördinaat met dezelfde factor is gewijzigd.[6] Dat wil zeggen, bepalen of de constante () is hetzelfde voor beide en waarden. - Bijvoorbeeld, als het eerste punt is en het tweede punt is , de x-coördinaat veranderd met een factor 2, sinds . De y-coördinaat veranderde ook met een factor 2 sindsdien . U kunt dus bevestigen dat de lijn twee variabelen vertegenwoordigt die direct proportioneel zijn.
Methode vier van vier:
Monsterproblemen afhandelen
-
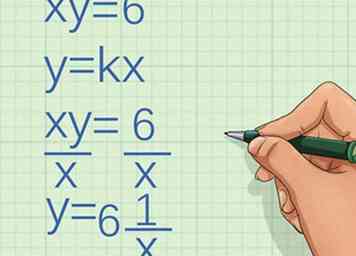 1 Kijk naar de vergelijking. Bepaal of de twee variabelen direct proportioneel zijn: .
1 Kijk naar de vergelijking. Bepaal of de twee variabelen direct proportioneel zijn: . - Onthoud dat als de variabelen direct proportioneel zijn, zij het patroon zullen volgen .
- Gebruik de algebra om de vergelijking te herschrijven.
- Isoleer de variabel door elke zijde te delen door :
- Isoleer de variabel door elke zijde te delen door :
- Beoordeel of de herschreven vergelijking het patroon volgt . In dit geval is de vergelijking niet, dus de variabelen zijn niet direct proportioneel. In feite zijn ze omgekeerd evenredig.[7]
-
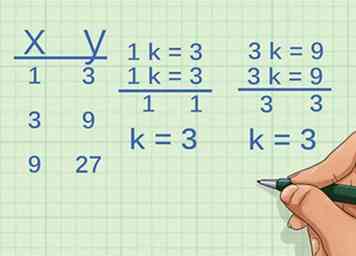 2 Overweeg de volgende reeks punten. Zijn de variabelen direct proportioneel?
2 Overweeg de volgende reeks punten. Zijn de variabelen direct proportioneel?
- Bepaal de groei van . Doe dit door de factor te vinden waarmee u de eerste x-coördinaat vermenigvuldigt om de tweede coördinaat te bereiken:
Dus de x-coördinaat groeit met factor 3. - Bepaal de groei van :
Dus de y-coördinaat groeit met factor 3. - Vergelijk de factor of constante van de twee variabelen. Ze groeien allebei met een factor 3. Daarom zijn de variabelen direct proportioneel.
- Bepaal de groei van . Doe dit door de factor te vinden waarmee u de eerste x-coördinaat vermenigvuldigt om de tweede coördinaat te bereiken:
-
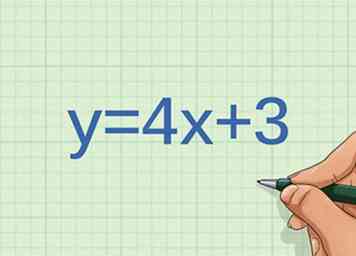 3 Beschouw een grafiek van de lijn . Toont de grafiek een directe verhouding tussen variabelen?
3 Beschouw een grafiek van de lijn . Toont de grafiek een directe verhouding tussen variabelen? - Let op of de lijn recht is. Omdat de vergelijking van de lijn in de vorm van een helling ligt, heeft deze een constante helling, wat betekent dat de lijn recht is. Dus potentieel zijn de variabelen direct proportioneel.
- Bepaal het y-snijpunt. Als de variabelen direct proportioneel zijn, zal de lijn het punt passeren . Het y-snijpunt van deze lijn is het punt . Dus de variabelen zijn niet direct proportioneel.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Begrijp de directe verhouding. Twee variabelen staan in directe verhouding als elke variabele met dezelfde snelheid verandert.[1] Met andere woorden, als
1 Begrijp de directe verhouding. Twee variabelen staan in directe verhouding als elke variabele met dezelfde snelheid verandert.[1] Met andere woorden, als 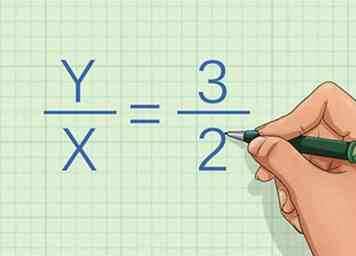 2 Noteer de vergelijking van de regel. De vergelijking heeft twee variabelen en een constante. Als u de vergelijking niet krijgt, kunt u deze methode niet gebruiken.
2 Noteer de vergelijking van de regel. De vergelijking heeft twee variabelen en een constante. Als u de vergelijking niet krijgt, kunt u deze methode niet gebruiken. 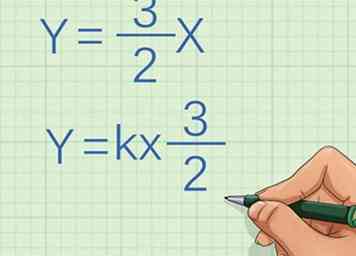 3 Herschrijf de vergelijking in de vorm van directe proportie of variatie. De vergelijking is
3 Herschrijf de vergelijking in de vorm van directe proportie of variatie. De vergelijking is  1 Identificeer de x-coördinaten van de eerste twee punten. Je zou een lijst met coördinaten moeten krijgen, of een grafiek hebben waaruit je de coördinaten van de punten kunt bepalen. Als u niet de coördinaten van punten op de lijn hebt, kunt u deze methode niet gebruiken.
1 Identificeer de x-coördinaten van de eerste twee punten. Je zou een lijst met coördinaten moeten krijgen, of een grafiek hebben waaruit je de coördinaten van de punten kunt bepalen. Als u niet de coördinaten van punten op de lijn hebt, kunt u deze methode niet gebruiken. 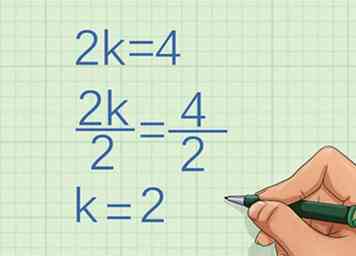 2 Bepaal de factor waarmee de
2 Bepaal de factor waarmee de 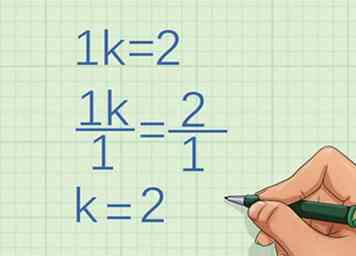 3 Bepaal de factor waarmee de
3 Bepaal de factor waarmee de  4 Vergelijk de constanten van de twee variabelen. Als
4 Vergelijk de constanten van de twee variabelen. Als  1 Let op of de lijn recht is. Als twee variabelen in verhouding zijn, is de regel die hen vertegenwoordigt recht.[4] Dit betekent dat de helling van de lijn constant is, of de vergelijking volgt
1 Let op of de lijn recht is. Als twee variabelen in verhouding zijn, is de regel die hen vertegenwoordigt recht.[4] Dit betekent dat de helling van de lijn constant is, of de vergelijking volgt  2 Bepaal het y-snijpunt. Het y-snijpunt is het punt waar de lijn de y-as kruist. Wanneer twee variabelen direct proportioneel zijn, zal hun lijn in de grafiek door de oorsprong lopen. De oorsprong is op het punt
2 Bepaal het y-snijpunt. Het y-snijpunt is het punt waar de lijn de y-as kruist. Wanneer twee variabelen direct proportioneel zijn, zal hun lijn in de grafiek door de oorsprong lopen. De oorsprong is op het punt  3 Zoek de coördinaten van twee punten op de lijn. Vergelijk de coördinaten met elkaar en bepaal of elke coördinaat met dezelfde factor is gewijzigd.[6] Dat wil zeggen, bepalen of de constante (
3 Zoek de coördinaten van twee punten op de lijn. Vergelijk de coördinaten met elkaar en bepaal of elke coördinaat met dezelfde factor is gewijzigd.[6] Dat wil zeggen, bepalen of de constante (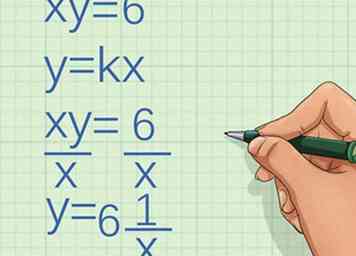 1 Kijk naar de vergelijking. Bepaal of de twee variabelen direct proportioneel zijn:
1 Kijk naar de vergelijking. Bepaal of de twee variabelen direct proportioneel zijn: 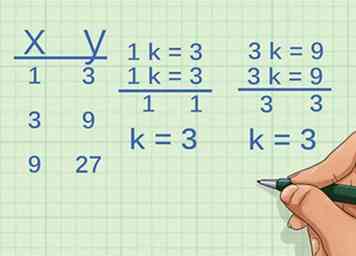 2 Overweeg de volgende reeks punten. Zijn de variabelen direct proportioneel?
2 Overweeg de volgende reeks punten. Zijn de variabelen direct proportioneel?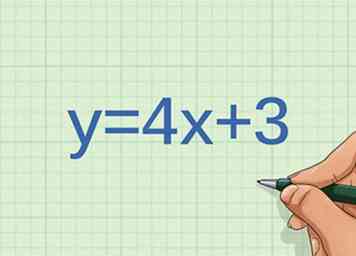 3 Beschouw een grafiek van de lijn
3 Beschouw een grafiek van de lijn