De schaalfactor, of lineaire schaalfactor, is de verhouding van twee overeenkomstige zijlengtes van vergelijkbare cijfers. Vergelijkbare figuren hebben dezelfde vorm maar zijn van verschillende grootte. De schaalfactor wordt gebruikt om elementaire geometrische problemen op te lossen. U kunt de schaalfactor gebruiken om de ontbrekende lengtes van een figuur te vinden. Omgekeerd kunt u de zijlengtes van twee vergelijkbare figuren gebruiken om de schaalfactor te berekenen. Deze problemen houden vermenigvuldiging in of vereisen dat u breuken vereenvoudigt.
Methode één van de vier:
De schaalfactor van vergelijkbare cijfers vinden
-
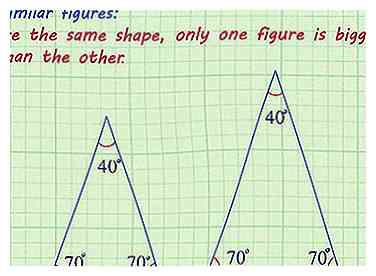 1 Controleer of de cijfers vergelijkbaar zijn. Vergelijkbare figuren, of vormen, zijn degenen waarin de hoeken congruent zijn en de lengte van de zijkanten in verhouding zijn. Vergelijkbare figuren hebben dezelfde vorm, slechts één figuur is groter dan de andere.[1]
1 Controleer of de cijfers vergelijkbaar zijn. Vergelijkbare figuren, of vormen, zijn degenen waarin de hoeken congruent zijn en de lengte van de zijkanten in verhouding zijn. Vergelijkbare figuren hebben dezelfde vorm, slechts één figuur is groter dan de andere.[1] - Het probleem zou je moeten vertellen dat de vormen gelijkaardig zijn, of het kan je laten zien dat de hoeken hetzelfde zijn, en anders aangeven dat de lengtes van de zijkant proportioneel zijn, op schaal staan, of dat ze met elkaar corresponderen.
-
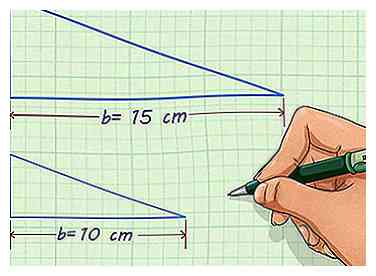 2 Zoek een corresponderende zijlengte op elk figuur. Mogelijk moet u de figuur draaien of omdraaien zodat de twee vormen op één lijn liggen en kunt u de bijbehorende lengtes van de zijkanten identificeren. Je moet de lengte van deze twee kanten krijgen, of ze kunnen meten.[2] Als u ten minste één zijlengte van elk figuur niet weet, kunt u de schaalfactor niet vinden.
2 Zoek een corresponderende zijlengte op elk figuur. Mogelijk moet u de figuur draaien of omdraaien zodat de twee vormen op één lijn liggen en kunt u de bijbehorende lengtes van de zijkanten identificeren. Je moet de lengte van deze twee kanten krijgen, of ze kunnen meten.[2] Als u ten minste één zijlengte van elk figuur niet weet, kunt u de schaalfactor niet vinden. - U hebt bijvoorbeeld een driehoek met een basis van 15 cm lang en een vergelijkbare driehoek met een basis van 10 cm lang.
-
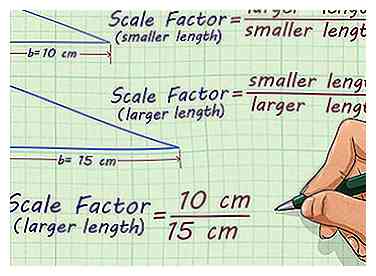 3 Stel een ratio in. Voor elk paar vergelijkbare figuren zijn er twee schaalfactoren: één die u gebruikt bij het opschalen en een schaal die u gebruikt bij het verkleinen. Als u opschaalt van een kleiner cijfer naar een groter cijfer, gebruikt u de verhouding . Als u verkleint van een grotere naar een kleinere, gebruik dan de verhouding .[3]
3 Stel een ratio in. Voor elk paar vergelijkbare figuren zijn er twee schaalfactoren: één die u gebruikt bij het opschalen en een schaal die u gebruikt bij het verkleinen. Als u opschaalt van een kleiner cijfer naar een groter cijfer, gebruikt u de verhouding . Als u verkleint van een grotere naar een kleinere, gebruik dan de verhouding .[3] - Als u bijvoorbeeld verkleint van een driehoek met een basis van 15 cm naar een basis van 10 cm, gebruikt u de verhouding .
Het invullen van de juiste waarden wordt het .
- Als u bijvoorbeeld verkleint van een driehoek met een basis van 15 cm naar een basis van 10 cm, gebruikt u de verhouding .
-
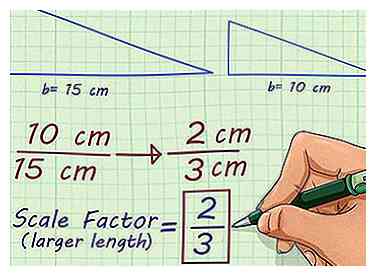 4 Vereenvoudig de verhouding. De vereenvoudigde verhouding of breuk geeft u uw schaalfactor. Als u verkleint, is uw schaalfactor een juiste breuk.[4] Als u opschaalt, wordt dit een geheel getal of een onjuiste breuk, die u kunt converteren naar een decimaal.
4 Vereenvoudig de verhouding. De vereenvoudigde verhouding of breuk geeft u uw schaalfactor. Als u verkleint, is uw schaalfactor een juiste breuk.[4] Als u opschaalt, wordt dit een geheel getal of een onjuiste breuk, die u kunt converteren naar een decimaal. - Bijvoorbeeld de verhouding vereenvoudigt tot . Dus de schaalfactor van twee driehoeken, één met een basis van 15 cm en één met een basis van 10 cm, is .
Methode twee van vier:
Een vergelijkbare figuur vinden met behulp van de schaalfactor
-
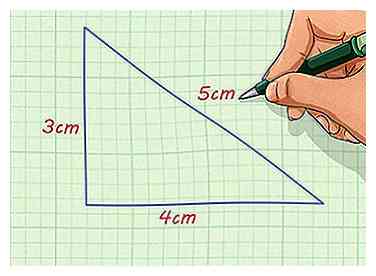 1 Zoek de lengte van de zijkant van de afbeelding. U zou één figuur moeten hebben waarvan de lengte van de zijkanten wordt gegeven of meetbaar. Als u de lengtes van de zijkant van het figuur niet kunt bepalen, kunt u geen vergelijkbaar figuur maken.
1 Zoek de lengte van de zijkant van de afbeelding. U zou één figuur moeten hebben waarvan de lengte van de zijkanten wordt gegeven of meetbaar. Als u de lengtes van de zijkant van het figuur niet kunt bepalen, kunt u geen vergelijkbaar figuur maken. - U hebt bijvoorbeeld een rechthoekige driehoek met zijden van 4 cm en 3 cm en een hypotenusa van 5 cm lang.
-
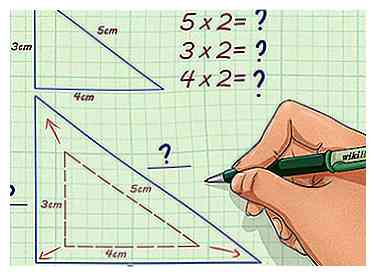 2 Bepaal of u omhoog of omlaag schaalt. Als u opschaalt, is uw ontbrekende figuur groter en is de schaalfactor een geheel getal, een onjuist deel of een decimaal. Als je kleiner wordt, zal je ontbrekende figuur kleiner zijn en zal je schaalfactor waarschijnlijk een goede fractie zijn.
2 Bepaal of u omhoog of omlaag schaalt. Als u opschaalt, is uw ontbrekende figuur groter en is de schaalfactor een geheel getal, een onjuist deel of een decimaal. Als je kleiner wordt, zal je ontbrekende figuur kleiner zijn en zal je schaalfactor waarschijnlijk een goede fractie zijn. - Als de schaalfactor bijvoorbeeld 2 is, wordt u opgeschaald en is het vergelijkbare cijfer groter dan het cijfer dat u heeft.
-
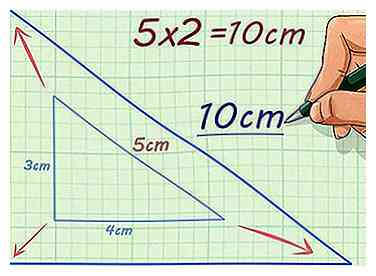 3 Vermenigvuldig de lengte van een zijde met de schaalfactor. De schaalfactor moet aan u worden gegeven. Wanneer u de zijlengte vermenigvuldigt met de schaalfactor, geeft dit u de ontbrekende overeenkomstige zijlengte op de vergelijkbare afbeelding.[5]
3 Vermenigvuldig de lengte van een zijde met de schaalfactor. De schaalfactor moet aan u worden gegeven. Wanneer u de zijlengte vermenigvuldigt met de schaalfactor, geeft dit u de ontbrekende overeenkomstige zijlengte op de vergelijkbare afbeelding.[5] - Als de hypotenusa van een rechthoekige driehoek bijvoorbeeld 5 cm lang is en de schaalfactor 2 is, zou u de hypotenusa van de vergelijkbare driehoek berekenen. . De vergelijkbare driehoek heeft dus een hypotenusa die 10 cm lang is.
-
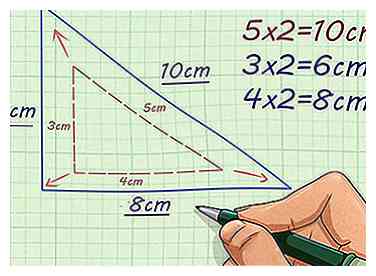 4 Zoek de resterende lengte van de zijkant van de afbeelding. Ga door met het vermenigvuldigen van elke zijde met de schaalfactor. Dit geeft je de overeenkomstige lengtes van het ontbrekende figuur.
4 Zoek de resterende lengte van de zijkant van de afbeelding. Ga door met het vermenigvuldigen van elke zijde met de schaalfactor. Dit geeft je de overeenkomstige lengtes van het ontbrekende figuur. - Als de basis van een rechthoekige driehoek bijvoorbeeld 3 cm lang is, met een schaalfactor van 2, zou u berekenen om de basis van de vergelijkbare driehoek te vinden. Als de hoogte van een rechthoekige driehoek 4 cm lang is, zou je een schaalfactor van 2 moeten berekenen om de hoogte van de vergelijkbare driehoek te vinden.
Methode drie van vier:
Monsterproblemen afhandelen
-
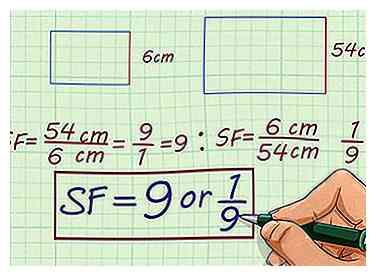 1 Zoek de schaalfactor van deze vergelijkbare cijfers: een rechthoek met een hoogte van 6 cm en een rechthoek met een hoogte van 54 cm.
1 Zoek de schaalfactor van deze vergelijkbare cijfers: een rechthoek met een hoogte van 6 cm en een rechthoek met een hoogte van 54 cm. - Maak een ratio die de twee hoogtes met elkaar vergelijkt. Schaalvergroting, de verhouding is . Schaalverlaging, de verhouding is .
- Vereenvoudig de verhouding. De ratio vereenvoudigt tot . De ratio vereenvoudigt tot . Dus de twee rechthoeken hebben een schaalfactor van of .
-
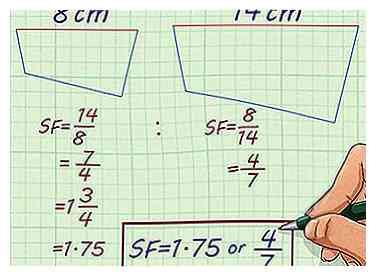 2 Probeer dit probleem. Een onregelmatige veelhoek is 14 cm lang op het breedste punt. Een soortgelijke onregelmatige veelhoek is 8 inch op het breedste punt. Wat is de schaalfactor?
2 Probeer dit probleem. Een onregelmatige veelhoek is 14 cm lang op het breedste punt. Een soortgelijke onregelmatige veelhoek is 8 inch op het breedste punt. Wat is de schaalfactor? - Onregelmatige figuren kunnen vergelijkbaar zijn als alle zijden evenredig zijn. U kunt dus een schaalfactor berekenen met elke dimensie die u krijgt.[6]
- Omdat u de breedte van elke polygoon kent, kunt u een ratio instellen om ze te vergelijken. Schaalvergroting, de verhouding is . Schaalverlaging, de verhouding is .
- Vereenvoudig de verhouding. De ratio vereenvoudigt tot . De ratio vereenvoudigt tot . Dus de twee onregelmatige veelhoeken hebben een schaalfactor van of .
-
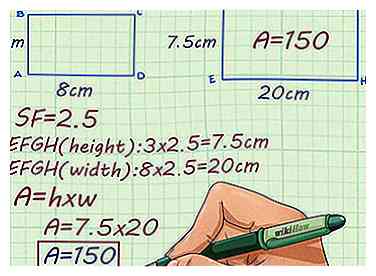 3 Gebruik de schaalfactor om dit probleem te verhelpen. Rechthoek ABCD is 8 cm x 3 cm. Rechthoek EFGH is een grotere, vergelijkbare rechthoek. Gebruik een schaalfactor van 2,5, wat is het gebied van Rechthoek EFGH?
3 Gebruik de schaalfactor om dit probleem te verhelpen. Rechthoek ABCD is 8 cm x 3 cm. Rechthoek EFGH is een grotere, vergelijkbare rechthoek. Gebruik een schaalfactor van 2,5, wat is het gebied van Rechthoek EFGH? - Vermenigvuldig de hoogte van rechthoek ABCD met de schaalfactor. Dit geeft je de hoogte van Rectangle EFGH: .
- Vermenigvuldig de breedte van rechthoek ABCD met de schaalfactor. Dit geeft je de breedte van Rectangle EFGH: .
- Vermenigvuldig de hoogte en breedte van de rechthoek EFGH om het gebied te vinden: . Het gebied van rechthoek EFGH is dus 150 vierkante centimeter.
Methode vier van vier:
De schaalfactor in de chemie vinden
-
 1 Verdeel de molaire massa van de verbinding door die van de empirische formule. Wanneer je de empirische formule van een chemische verbinding hebt en je de moleculaire formule van diezelfde chemische verbinding moet vinden, kun je de schaalfactor vinden die je nodig hebt door de molecuulmassa van de verbinding te delen door de molecuulmassa van de empirische formule.
1 Verdeel de molaire massa van de verbinding door die van de empirische formule. Wanneer je de empirische formule van een chemische verbinding hebt en je de moleculaire formule van diezelfde chemische verbinding moet vinden, kun je de schaalfactor vinden die je nodig hebt door de molecuulmassa van de verbinding te delen door de molecuulmassa van de empirische formule. - U moet bijvoorbeeld de molecuulmassa van een H2O-verbinding met een molecuulmassa van 54,05 g / mol vinden.
- De molmassa van H2O is 18,0152 g / mol.
- Zoek de schaalfactor door de molecuulmassa van de verbinding te delen door de molecuulmassa van de empirische formule:
- Schaalfactor = 54.05 / 18.0152 = 3
- U moet bijvoorbeeld de molecuulmassa van een H2O-verbinding met een molecuulmassa van 54,05 g / mol vinden.
-
 2 Vermenigvuldig de empirische formule met de schaalfactor. Vermenigvuldig de subscripts van elk element binnen de empirische formule met de schaalfactor die u zojuist hebt berekend. Hiermee krijgt u de molecuulformule van het monster van de chemische verbinding dat bij het probleem is betrokken.
2 Vermenigvuldig de empirische formule met de schaalfactor. Vermenigvuldig de subscripts van elk element binnen de empirische formule met de schaalfactor die u zojuist hebt berekend. Hiermee krijgt u de molecuulformule van het monster van de chemische verbinding dat bij het probleem is betrokken. - Om bijvoorbeeld de molecuulformule van de betreffende verbinding te vinden, vermenigvuldigt u de subscripts van H20 met de schaalfactor van 3.
- H2O * 3 = H6O3
- Om bijvoorbeeld de molecuulformule van de betreffende verbinding te vinden, vermenigvuldigt u de subscripts van H20 met de schaalfactor van 3.
-
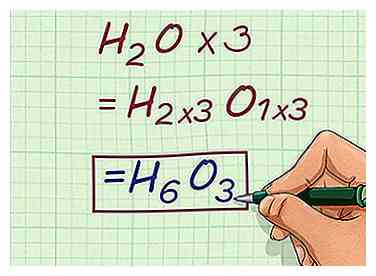 3 Schrijf het antwoord. Met dit antwoord hebt u met succes het antwoord gevonden voor de empirische formule en de molecuulformule van de chemische verbinding die bij het probleem is betrokken.
3 Schrijf het antwoord. Met dit antwoord hebt u met succes het antwoord gevonden voor de empirische formule en de molecuulformule van de chemische verbinding die bij het probleem is betrokken. - De schaalfactor voor de verbinding is bijvoorbeeld 3. De molecuulformule van de verbinding is H6O3.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Controleer of de cijfers vergelijkbaar zijn. Vergelijkbare figuren, of vormen, zijn degenen waarin de hoeken congruent zijn en de lengte van de zijkanten in verhouding zijn. Vergelijkbare figuren hebben dezelfde vorm, slechts één figuur is groter dan de andere.[1]
1 Controleer of de cijfers vergelijkbaar zijn. Vergelijkbare figuren, of vormen, zijn degenen waarin de hoeken congruent zijn en de lengte van de zijkanten in verhouding zijn. Vergelijkbare figuren hebben dezelfde vorm, slechts één figuur is groter dan de andere.[1]  2 Zoek een corresponderende zijlengte op elk figuur. Mogelijk moet u de figuur draaien of omdraaien zodat de twee vormen op één lijn liggen en kunt u de bijbehorende lengtes van de zijkanten identificeren. Je moet de lengte van deze twee kanten krijgen, of ze kunnen meten.[2] Als u ten minste één zijlengte van elk figuur niet weet, kunt u de schaalfactor niet vinden.
2 Zoek een corresponderende zijlengte op elk figuur. Mogelijk moet u de figuur draaien of omdraaien zodat de twee vormen op één lijn liggen en kunt u de bijbehorende lengtes van de zijkanten identificeren. Je moet de lengte van deze twee kanten krijgen, of ze kunnen meten.[2] Als u ten minste één zijlengte van elk figuur niet weet, kunt u de schaalfactor niet vinden.  3 Stel een ratio in. Voor elk paar vergelijkbare figuren zijn er twee schaalfactoren: één die u gebruikt bij het opschalen en een schaal die u gebruikt bij het verkleinen. Als u opschaalt van een kleiner cijfer naar een groter cijfer, gebruikt u de verhouding
3 Stel een ratio in. Voor elk paar vergelijkbare figuren zijn er twee schaalfactoren: één die u gebruikt bij het opschalen en een schaal die u gebruikt bij het verkleinen. Als u opschaalt van een kleiner cijfer naar een groter cijfer, gebruikt u de verhouding  4 Vereenvoudig de verhouding. De vereenvoudigde verhouding of breuk geeft u uw schaalfactor. Als u verkleint, is uw schaalfactor een juiste breuk.[4] Als u opschaalt, wordt dit een geheel getal of een onjuiste breuk, die u kunt converteren naar een decimaal.
4 Vereenvoudig de verhouding. De vereenvoudigde verhouding of breuk geeft u uw schaalfactor. Als u verkleint, is uw schaalfactor een juiste breuk.[4] Als u opschaalt, wordt dit een geheel getal of een onjuiste breuk, die u kunt converteren naar een decimaal.  1 Zoek de lengte van de zijkant van de afbeelding. U zou één figuur moeten hebben waarvan de lengte van de zijkanten wordt gegeven of meetbaar. Als u de lengtes van de zijkant van het figuur niet kunt bepalen, kunt u geen vergelijkbaar figuur maken.
1 Zoek de lengte van de zijkant van de afbeelding. U zou één figuur moeten hebben waarvan de lengte van de zijkanten wordt gegeven of meetbaar. Als u de lengtes van de zijkant van het figuur niet kunt bepalen, kunt u geen vergelijkbaar figuur maken.  2 Bepaal of u omhoog of omlaag schaalt. Als u opschaalt, is uw ontbrekende figuur groter en is de schaalfactor een geheel getal, een onjuist deel of een decimaal. Als je kleiner wordt, zal je ontbrekende figuur kleiner zijn en zal je schaalfactor waarschijnlijk een goede fractie zijn.
2 Bepaal of u omhoog of omlaag schaalt. Als u opschaalt, is uw ontbrekende figuur groter en is de schaalfactor een geheel getal, een onjuist deel of een decimaal. Als je kleiner wordt, zal je ontbrekende figuur kleiner zijn en zal je schaalfactor waarschijnlijk een goede fractie zijn.  3 Vermenigvuldig de lengte van een zijde met de schaalfactor. De schaalfactor moet aan u worden gegeven. Wanneer u de zijlengte vermenigvuldigt met de schaalfactor, geeft dit u de ontbrekende overeenkomstige zijlengte op de vergelijkbare afbeelding.[5]
3 Vermenigvuldig de lengte van een zijde met de schaalfactor. De schaalfactor moet aan u worden gegeven. Wanneer u de zijlengte vermenigvuldigt met de schaalfactor, geeft dit u de ontbrekende overeenkomstige zijlengte op de vergelijkbare afbeelding.[5]  4 Zoek de resterende lengte van de zijkant van de afbeelding. Ga door met het vermenigvuldigen van elke zijde met de schaalfactor. Dit geeft je de overeenkomstige lengtes van het ontbrekende figuur.
4 Zoek de resterende lengte van de zijkant van de afbeelding. Ga door met het vermenigvuldigen van elke zijde met de schaalfactor. Dit geeft je de overeenkomstige lengtes van het ontbrekende figuur.  1 Zoek de schaalfactor van deze vergelijkbare cijfers: een rechthoek met een hoogte van 6 cm en een rechthoek met een hoogte van 54 cm.
1 Zoek de schaalfactor van deze vergelijkbare cijfers: een rechthoek met een hoogte van 6 cm en een rechthoek met een hoogte van 54 cm.  2 Probeer dit probleem. Een onregelmatige veelhoek is 14 cm lang op het breedste punt. Een soortgelijke onregelmatige veelhoek is 8 inch op het breedste punt. Wat is de schaalfactor?
2 Probeer dit probleem. Een onregelmatige veelhoek is 14 cm lang op het breedste punt. Een soortgelijke onregelmatige veelhoek is 8 inch op het breedste punt. Wat is de schaalfactor?  3 Gebruik de schaalfactor om dit probleem te verhelpen. Rechthoek ABCD is 8 cm x 3 cm. Rechthoek EFGH is een grotere, vergelijkbare rechthoek. Gebruik een schaalfactor van 2,5, wat is het gebied van Rechthoek EFGH?
3 Gebruik de schaalfactor om dit probleem te verhelpen. Rechthoek ABCD is 8 cm x 3 cm. Rechthoek EFGH is een grotere, vergelijkbare rechthoek. Gebruik een schaalfactor van 2,5, wat is het gebied van Rechthoek EFGH?  1 Verdeel de molaire massa van de verbinding door die van de empirische formule. Wanneer je de empirische formule van een chemische verbinding hebt en je de moleculaire formule van diezelfde chemische verbinding moet vinden, kun je de schaalfactor vinden die je nodig hebt door de molecuulmassa van de verbinding te delen door de molecuulmassa van de empirische formule.
1 Verdeel de molaire massa van de verbinding door die van de empirische formule. Wanneer je de empirische formule van een chemische verbinding hebt en je de moleculaire formule van diezelfde chemische verbinding moet vinden, kun je de schaalfactor vinden die je nodig hebt door de molecuulmassa van de verbinding te delen door de molecuulmassa van de empirische formule.  2 Vermenigvuldig de empirische formule met de schaalfactor. Vermenigvuldig de subscripts van elk element binnen de empirische formule met de schaalfactor die u zojuist hebt berekend. Hiermee krijgt u de molecuulformule van het monster van de chemische verbinding dat bij het probleem is betrokken.
2 Vermenigvuldig de empirische formule met de schaalfactor. Vermenigvuldig de subscripts van elk element binnen de empirische formule met de schaalfactor die u zojuist hebt berekend. Hiermee krijgt u de molecuulformule van het monster van de chemische verbinding dat bij het probleem is betrokken. 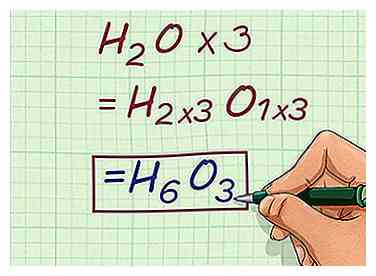 3 Schrijf het antwoord. Met dit antwoord hebt u met succes het antwoord gevonden voor de empirische formule en de molecuulformule van de chemische verbinding die bij het probleem is betrokken.
3 Schrijf het antwoord. Met dit antwoord hebt u met succes het antwoord gevonden voor de empirische formule en de molecuulformule van de chemische verbinding die bij het probleem is betrokken.