De determinant van een matrix wordt vaak gebruikt in calculus, lineaire algebra en geavanceerde geometrie. Het vinden van de determinant van een matrix kan in het begin verwarrend zijn, maar het wordt gemakkelijker als je het een paar keer doet.
Deel een van de twee:
De determinant vinden
-
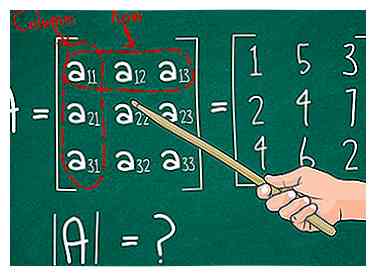 1 Schrijf je 3 x 3 matrix. We beginnen met een matrix van 3 x 3 en proberen de bepalende factor te vinden | A |. Dit is de algemene matrixnotatie die we zullen gebruiken en onze voorbeeldmatrix:
1 Schrijf je 3 x 3 matrix. We beginnen met een matrix van 3 x 3 en proberen de bepalende factor te vinden | A |. Dit is de algemene matrixnotatie die we zullen gebruiken en onze voorbeeldmatrix: -
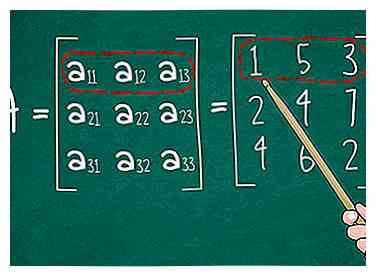 2 Kies een enkele rij of kolom. Dit wordt uw referentierij of -kolom. U krijgt hetzelfde antwoord, ongeacht welke u kiest. Kies voor nu gewoon de eerste rij. Later zullen we wat advies geven over het kiezen van de gemakkelijkste optie om te berekenen.
2 Kies een enkele rij of kolom. Dit wordt uw referentierij of -kolom. U krijgt hetzelfde antwoord, ongeacht welke u kiest. Kies voor nu gewoon de eerste rij. Later zullen we wat advies geven over het kiezen van de gemakkelijkste optie om te berekenen. - Laten we de eerste rij van onze voorbeeldmatrix A kiezen. Omcirkel de 1 5 3. In algemene bewoordingen, cirkel a11 een12 een13.
-
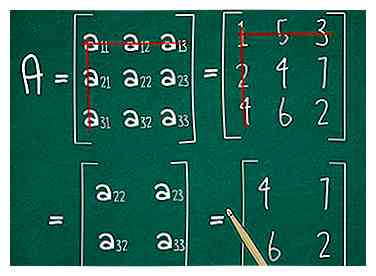 3 Steek de rij en kolom van je eerste element eruit. Kijk naar de rij of kolom die u hebt omcirkeld en selecteer het eerste element. Trek een lijn door de rij en kolom. Je zou vier cijfers moeten hebben. We behandelen deze als een 2 x 2 matrix.
3 Steek de rij en kolom van je eerste element eruit. Kijk naar de rij of kolom die u hebt omcirkeld en selecteer het eerste element. Trek een lijn door de rij en kolom. Je zou vier cijfers moeten hebben. We behandelen deze als een 2 x 2 matrix. - In ons voorbeeld is onze referentierij 1 5 3. De eerste element staat in rij 1 en kolom 1. Haal rij 1 en kolom 1 door elkaar. Noteer de resterende elementen als een 2 x 2 matrix:
-
1 5 324 746 2
-
 4 Zoek de determinant van de 2 x 2 matrix. Onthoud, de matrix heeft een determinant van ad - bc.[1] Mogelijk hebt u dit geleerd door een X over de matrix van 2 x 2 te tekenen. Vermenigvuldig de twee nummers verbonden door de \ van de X. Trek vervolgens het product af van de twee nummers verbonden door de /. Gebruik deze formule om de door u gevonden matrix te berekenen.
4 Zoek de determinant van de 2 x 2 matrix. Onthoud, de matrix heeft een determinant van ad - bc.[1] Mogelijk hebt u dit geleerd door een X over de matrix van 2 x 2 te tekenen. Vermenigvuldig de twee nummers verbonden door de \ van de X. Trek vervolgens het product af van de twee nummers verbonden door de /. Gebruik deze formule om de door u gevonden matrix te berekenen. - In ons voorbeeld de determinant van de matrix = 4 * 2 - 7 * 6 = -34.
- Deze determinant wordt de mineur van het element dat we in onze originele matrix hebben gekozen.[2] In dit geval hebben we de minderjarige gevonden een11.
-
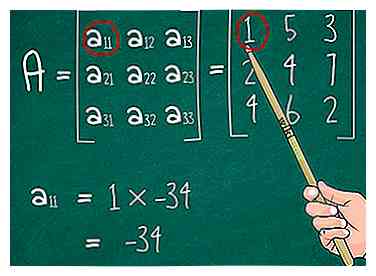 5 Vermenigvuldig het antwoord met het door u gekozen element. Vergeet niet dat je een element uit je referentierij (of kolom) hebt geselecteerd toen je besloot welke rij en kolom je wilt overschrijden. Vermenigvuldig dit element met de determinant die u zojuist hebt berekend voor de 2x2-matrix.
5 Vermenigvuldig het antwoord met het door u gekozen element. Vergeet niet dat je een element uit je referentierij (of kolom) hebt geselecteerd toen je besloot welke rij en kolom je wilt overschrijden. Vermenigvuldig dit element met de determinant die u zojuist hebt berekend voor de 2x2-matrix. - In ons voorbeeld hebben we een geselecteerd11, die de waarde 1 had. Vermenigvuldig dit met -34 (de determinant van de 2x2) om 1 * -34 = te krijgen -34.
-
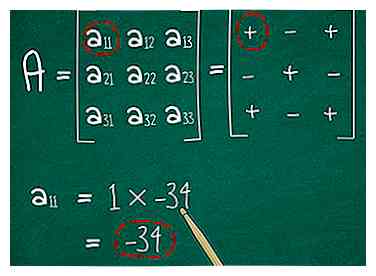 6 Bepaal het teken van uw antwoord. Vervolgens vermenigvuldig je je antwoord met 1 of met -1 om het antwoord te krijgen cofactor van uw gekozen element. Welke je gebruikt hangt af van waar het element in de 3x3 matrix is geplaatst. Onthoud dit eenvoudige tekenschema om te volgen welk element veroorzaakt welke:
6 Bepaal het teken van uw antwoord. Vervolgens vermenigvuldig je je antwoord met 1 of met -1 om het antwoord te krijgen cofactor van uw gekozen element. Welke je gebruikt hangt af van waar het element in de 3x3 matrix is geplaatst. Onthoud dit eenvoudige tekenschema om te volgen welk element veroorzaakt welke: - + - +
- + -
+ - + - Omdat we hebben gekozen een11, gemarkeerd met een +, vermenigvuldigen we het aantal met +1. (Met andere woorden, laat het met rust.) Het antwoord is nog steeds -34.
- U kunt ook het bord met de formule (-1) vindeni + j, waar ik en j zijn de rij en kolom van het element.[3]
- + - +
-
 7 Herhaal dit proces voor het tweede element in uw referentierij of kolom. Keer terug naar de oorspronkelijke matrix van 3x3, met de rij of kolom die u eerder hebt omcirkeld. Herhaal hetzelfde proces met dit element:
7 Herhaal dit proces voor het tweede element in uw referentierij of kolom. Keer terug naar de oorspronkelijke matrix van 3x3, met de rij of kolom die u eerder hebt omcirkeld. Herhaal hetzelfde proces met dit element: - Steek de rij en kolom van dat element uit. Selecteer in dit geval element a12 (met een waarde van 5). Rij één (1 5 3) en kolom twee doorsnijden .
- Behandel de resterende elementen als een matrix van 2x2. In ons voorbeeld is de matrix dat
- Zoek de determinant van deze 2x2-matrix. Gebruik de ad - bc-formule. (2 * 2 - 7 * 4 = -24)
- Vermenigvuldig met het gekozen element van de 3x3-matrix. -24 * 5 = -120
- Bepaal of u wilt vermenigvuldigen met -1. Gebruik de tekenkaart of de (-1)ij formule. We kozen voor element a12, dat is - op de tekentabel. We moeten het teken van ons antwoord veranderen: (-1) * (- 120) = 120.
-
 8 Herhaal met het derde element. Je hebt nog een cofactor te vinden. Bereken i voor de derde term in uw referentierij of kolom. Hier is een kort overzicht van hoe je de cofactor van een zou berekenen13 in ons voorbeeld:
8 Herhaal met het derde element. Je hebt nog een cofactor te vinden. Bereken i voor de derde term in uw referentierij of kolom. Hier is een kort overzicht van hoe je de cofactor van een zou berekenen13 in ons voorbeeld: - Steek rij 1 en kolom 3 eruit om te krijgen
- De bepalende factor is 2 * 6 - 4 * 4 = -4.
- Vermenigvuldigen met element a13: -4 * 3 = -12.
- Element a13 is + op het tekenbord, dus het antwoord is -12.
-
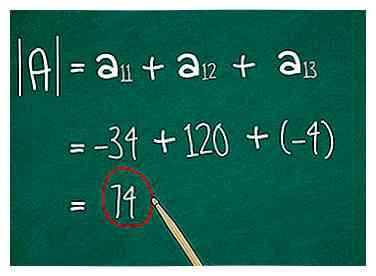 9 Voeg uw drie resultaten samen toe. Dit is de laatste stap. U hebt drie co-factoren berekend, één voor elk element in één rij of kolom. Voeg deze samen toe en je hebt de determinant van de 3x3 matrix gevonden.
9 Voeg uw drie resultaten samen toe. Dit is de laatste stap. U hebt drie co-factoren berekend, één voor elk element in één rij of kolom. Voeg deze samen toe en je hebt de determinant van de 3x3 matrix gevonden. - In ons voorbeeld is de bepalende factor -34 + 120 + -12 = 74.
Deel twee van twee:
Het probleem eenvoudiger maken
-
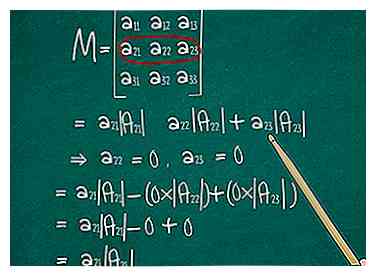 1 Kies de referentie met de meeste nullen. Vergeet niet dat je kunt kiezen ieder rij of kolom als uw referentie. Je krijgt hetzelfde antwoord, ongeacht wat je kiest. Als u een rij of kolom kiest met nullen, hoeft u alleen de cofactor voor de niet-nulelementen te berekenen. Dit is waarom:
1 Kies de referentie met de meeste nullen. Vergeet niet dat je kunt kiezen ieder rij of kolom als uw referentie. Je krijgt hetzelfde antwoord, ongeacht wat je kiest. Als u een rij of kolom kiest met nullen, hoeft u alleen de cofactor voor de niet-nulelementen te berekenen. Dit is waarom: - Laten we zeggen dat u rij 2 kiest, met elementen a21, een22, en een23. Om dit probleem op te lossen, bekijken we drie verschillende 2x2-matrices. Laten we ze A noemen21, EEN22, en een23.
- De determinant van de 3x3-matrix is een21| A21| - een22| A22| + a23| A23|.
- Als voorwaarden a22 en een23 zijn beide 0, onze formule wordt een21| A21| - 0 * | A22| + 0 * | A23| = a21| A21| - 0 + 0 = a21| A21|. Nu hoeven we alleen de cofactor van een enkel element te berekenen.
-
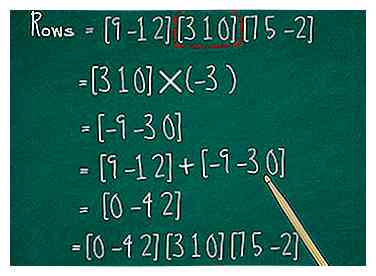 2 Gebruik rijtoevoeging om de matrix gemakkelijker te maken. Als u de waarden van één rij neemt en deze aan een andere rij toevoegt, verandert de determinant van de matrix niet. Hetzelfde geldt voor kolommen. U kunt dit herhaaldelijk doen - of de waarden vermenigvuldigen met een constante vóór het toevoegen - om zo veel mogelijk nullen in de matrix te krijgen. Dit kan u veel tijd besparen.
2 Gebruik rijtoevoeging om de matrix gemakkelijker te maken. Als u de waarden van één rij neemt en deze aan een andere rij toevoegt, verandert de determinant van de matrix niet. Hetzelfde geldt voor kolommen. U kunt dit herhaaldelijk doen - of de waarden vermenigvuldigen met een constante vóór het toevoegen - om zo veel mogelijk nullen in de matrix te krijgen. Dit kan u veel tijd besparen. - Stel dat u een matrix van 3 x 3 hebt:
- Om de 9 in positie te annuleren, a11, we kunnen de tweede rij vermenigvuldigen met -3 en het resultaat toevoegen aan de eerste. De nieuwe eerste rij is [9-1 2] + [-9 -3 0] = [0 -4 2].
- De nieuwe matrix is Probeer dezelfde truc met kolommen te gebruiken om a te draaien12 in een 0 ook.
-
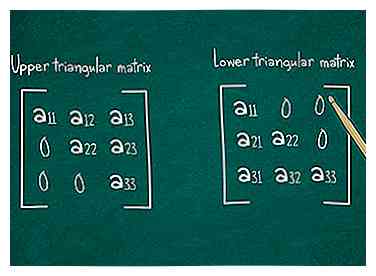 3 Leer de snelkoppeling voor driehoekige matrices. In deze speciale gevallen is de determinant eenvoudigweg het product van de elementen langs de hoofddiagonaal, van een11 in de linkerbovenhoek naar a33 rechtsonder. We hebben het nog steeds over 3x3-matrices, maar 'driehoekige' hebben speciale patronen van -nul waarden:[4]
3 Leer de snelkoppeling voor driehoekige matrices. In deze speciale gevallen is de determinant eenvoudigweg het product van de elementen langs de hoofddiagonaal, van een11 in de linkerbovenhoek naar a33 rechtsonder. We hebben het nog steeds over 3x3-matrices, maar 'driehoekige' hebben speciale patronen van -nul waarden:[4] - Bovenste driehoekige matrix: alle niet-nulelementen bevinden zich op of boven de hoofddiagonaal. Alles hieronder is een nul.
- Lagere driehoekige matrix: alle niet-nulelementen bevinden zich op of onder de hoofddiagonaal.
- Diagonale matrix: alle niet-nulelementen bevinden zich op de hoofddiagonaal. (Een subset van het bovenstaande.)
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
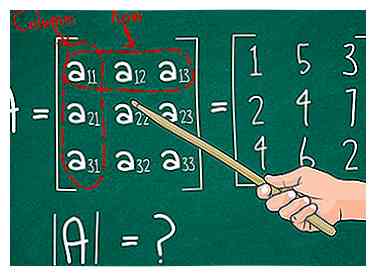 1 Schrijf je 3 x 3 matrix. We beginnen met een matrix van 3 x 3 en proberen de bepalende factor te vinden | A |. Dit is de algemene matrixnotatie die we zullen gebruiken en onze voorbeeldmatrix:
1 Schrijf je 3 x 3 matrix. We beginnen met een matrix van 3 x 3 en proberen de bepalende factor te vinden | A |. Dit is de algemene matrixnotatie die we zullen gebruiken en onze voorbeeldmatrix: 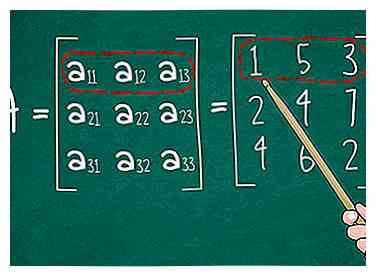 2 Kies een enkele rij of kolom. Dit wordt uw referentierij of -kolom. U krijgt hetzelfde antwoord, ongeacht welke u kiest. Kies voor nu gewoon de eerste rij. Later zullen we wat advies geven over het kiezen van de gemakkelijkste optie om te berekenen.
2 Kies een enkele rij of kolom. Dit wordt uw referentierij of -kolom. U krijgt hetzelfde antwoord, ongeacht welke u kiest. Kies voor nu gewoon de eerste rij. Later zullen we wat advies geven over het kiezen van de gemakkelijkste optie om te berekenen.  3 Steek de rij en kolom van je eerste element eruit. Kijk naar de rij of kolom die u hebt omcirkeld en selecteer het eerste element. Trek een lijn door de rij en kolom. Je zou vier cijfers moeten hebben. We behandelen deze als een 2 x 2 matrix.
3 Steek de rij en kolom van je eerste element eruit. Kijk naar de rij of kolom die u hebt omcirkeld en selecteer het eerste element. Trek een lijn door de rij en kolom. Je zou vier cijfers moeten hebben. We behandelen deze als een 2 x 2 matrix.  4 Zoek de determinant van de 2 x 2 matrix. Onthoud, de matrix
4 Zoek de determinant van de 2 x 2 matrix. Onthoud, de matrix 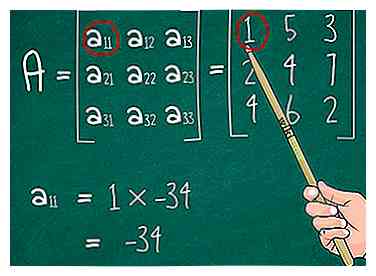 5 Vermenigvuldig het antwoord met het door u gekozen element. Vergeet niet dat je een element uit je referentierij (of kolom) hebt geselecteerd toen je besloot welke rij en kolom je wilt overschrijden. Vermenigvuldig dit element met de determinant die u zojuist hebt berekend voor de 2x2-matrix.
5 Vermenigvuldig het antwoord met het door u gekozen element. Vergeet niet dat je een element uit je referentierij (of kolom) hebt geselecteerd toen je besloot welke rij en kolom je wilt overschrijden. Vermenigvuldig dit element met de determinant die u zojuist hebt berekend voor de 2x2-matrix.  6 Bepaal het teken van uw antwoord. Vervolgens vermenigvuldig je je antwoord met 1 of met -1 om het antwoord te krijgen cofactor van uw gekozen element. Welke je gebruikt hangt af van waar het element in de 3x3 matrix is geplaatst. Onthoud dit eenvoudige tekenschema om te volgen welk element veroorzaakt welke:
6 Bepaal het teken van uw antwoord. Vervolgens vermenigvuldig je je antwoord met 1 of met -1 om het antwoord te krijgen cofactor van uw gekozen element. Welke je gebruikt hangt af van waar het element in de 3x3 matrix is geplaatst. Onthoud dit eenvoudige tekenschema om te volgen welk element veroorzaakt welke:  7 Herhaal dit proces voor het tweede element in uw referentierij of kolom. Keer terug naar de oorspronkelijke matrix van 3x3, met de rij of kolom die u eerder hebt omcirkeld. Herhaal hetzelfde proces met dit element:
7 Herhaal dit proces voor het tweede element in uw referentierij of kolom. Keer terug naar de oorspronkelijke matrix van 3x3, met de rij of kolom die u eerder hebt omcirkeld. Herhaal hetzelfde proces met dit element:  8 Herhaal met het derde element. Je hebt nog een cofactor te vinden. Bereken i voor de derde term in uw referentierij of kolom. Hier is een kort overzicht van hoe je de cofactor van een zou berekenen13 in ons voorbeeld:
8 Herhaal met het derde element. Je hebt nog een cofactor te vinden. Bereken i voor de derde term in uw referentierij of kolom. Hier is een kort overzicht van hoe je de cofactor van een zou berekenen13 in ons voorbeeld: 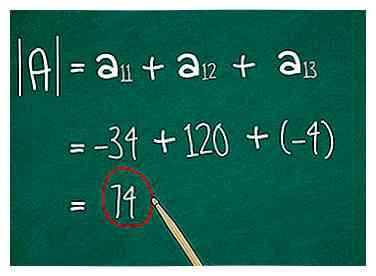 9 Voeg uw drie resultaten samen toe. Dit is de laatste stap. U hebt drie co-factoren berekend, één voor elk element in één rij of kolom. Voeg deze samen toe en je hebt de determinant van de 3x3 matrix gevonden.
9 Voeg uw drie resultaten samen toe. Dit is de laatste stap. U hebt drie co-factoren berekend, één voor elk element in één rij of kolom. Voeg deze samen toe en je hebt de determinant van de 3x3 matrix gevonden. 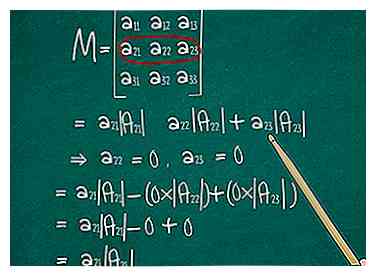 1 Kies de referentie met de meeste nullen. Vergeet niet dat je kunt kiezen ieder rij of kolom als uw referentie. Je krijgt hetzelfde antwoord, ongeacht wat je kiest. Als u een rij of kolom kiest met nullen, hoeft u alleen de cofactor voor de niet-nulelementen te berekenen. Dit is waarom:
1 Kies de referentie met de meeste nullen. Vergeet niet dat je kunt kiezen ieder rij of kolom als uw referentie. Je krijgt hetzelfde antwoord, ongeacht wat je kiest. Als u een rij of kolom kiest met nullen, hoeft u alleen de cofactor voor de niet-nulelementen te berekenen. Dit is waarom: 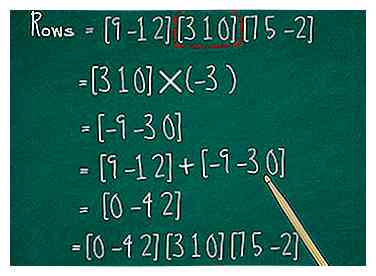 2 Gebruik rijtoevoeging om de matrix gemakkelijker te maken. Als u de waarden van één rij neemt en deze aan een andere rij toevoegt, verandert de determinant van de matrix niet. Hetzelfde geldt voor kolommen. U kunt dit herhaaldelijk doen - of de waarden vermenigvuldigen met een constante vóór het toevoegen - om zo veel mogelijk nullen in de matrix te krijgen. Dit kan u veel tijd besparen.
2 Gebruik rijtoevoeging om de matrix gemakkelijker te maken. Als u de waarden van één rij neemt en deze aan een andere rij toevoegt, verandert de determinant van de matrix niet. Hetzelfde geldt voor kolommen. U kunt dit herhaaldelijk doen - of de waarden vermenigvuldigen met een constante vóór het toevoegen - om zo veel mogelijk nullen in de matrix te krijgen. Dit kan u veel tijd besparen.  3 Leer de snelkoppeling voor driehoekige matrices. In deze speciale gevallen is de determinant eenvoudigweg het product van de elementen langs de hoofddiagonaal, van een11 in de linkerbovenhoek naar a33 rechtsonder. We hebben het nog steeds over 3x3-matrices, maar 'driehoekige' hebben speciale patronen van -nul waarden:[4]
3 Leer de snelkoppeling voor driehoekige matrices. In deze speciale gevallen is de determinant eenvoudigweg het product van de elementen langs de hoofddiagonaal, van een11 in de linkerbovenhoek naar a33 rechtsonder. We hebben het nog steeds over 3x3-matrices, maar 'driehoekige' hebben speciale patronen van -nul waarden:[4]