Inverse operaties worden vaak gebruikt in de algebra om te vereenvoudigen wat anders moeilijk zou kunnen zijn. Als een probleem bijvoorbeeld vereist dat u deelt door een breuk, kunt u gemakkelijker vermenigvuldigen met het omgekeerde. Dit is een inverse operatie. Evenzo, aangezien er geen divisie-operator voor matrices is, moet u vermenigvuldigen met de inverse matrix. Het berekenen van de inverse van een 3x3 matrix met de hand is een saaie klus, maar het is de moeite van het bekijken waard. U kunt de inverse ook vinden met behulp van een geavanceerde grafische rekenmachine.
Methode één van de drie:
De Adjugate Matrix maken om de inverse matrix te vinden
-
 1 Controleer de determinant van de matrix. U moet de determinant van de matrix als een eerste stap berekenen. Als de determinant 0 is, is uw werk voltooid, omdat de matrix geen inverse heeft. De determinant van matrix M kan symbolisch worden weergegeven als det (M).[1]
1 Controleer de determinant van de matrix. U moet de determinant van de matrix als een eerste stap berekenen. Als de determinant 0 is, is uw werk voltooid, omdat de matrix geen inverse heeft. De determinant van matrix M kan symbolisch worden weergegeven als det (M).[1] - Zoek voor een matrix van 3x3 eerst de determinant
- Zie Find the Determinant of a 3X3 Matrix voor meer informatie over het vinden van de determinant van een matrix.
-
 2 Transponeer de originele matrix. Transposeriemiddelen die de matrix om de hoofddiagonaal weergeven, of equivalent, het (i, j) ste element en het (j, i) ste omwisselen. Wanneer u de termen van de matrix transponeert, zou u moeten zien dat de hoofddiagonaal (van linksboven naar rechtsonder) ongewijzigd is.[2]
2 Transponeer de originele matrix. Transposeriemiddelen die de matrix om de hoofddiagonaal weergeven, of equivalent, het (i, j) ste element en het (j, i) ste omwisselen. Wanneer u de termen van de matrix transponeert, zou u moeten zien dat de hoofddiagonaal (van linksboven naar rechtsonder) ongewijzigd is.[2] - Een andere manier om aan transponeren te denken, is dat je de eerste rij als de eerste kolom herschrijft, de middelste rij de middelste kolom en de derde rij de derde kolom. Let op de gekleurde elementen in het bovenstaande diagram en zie waar de nummers van positie zijn veranderd.
-
 3 Zoek de determinant van elk van de 2x2 minor matrices. Elk item van de nieuw getransponeerde 3x3-matrix is gekoppeld aan een overeenkomstige 2x2 "ondergeschikte" matrix. Om de juiste kleine matrix voor elke term te vinden, markeert u eerst de rij en kolom van de term waarmee u begint. Dit moet vijf termen van de matrix bevatten. De overige vier termen vormen de secundaire matrix.[3]
3 Zoek de determinant van elk van de 2x2 minor matrices. Elk item van de nieuw getransponeerde 3x3-matrix is gekoppeld aan een overeenkomstige 2x2 "ondergeschikte" matrix. Om de juiste kleine matrix voor elke term te vinden, markeert u eerst de rij en kolom van de term waarmee u begint. Dit moet vijf termen van de matrix bevatten. De overige vier termen vormen de secundaire matrix.[3] - Als u in het bovenstaande voorbeeld de secundaire matrix van de term in de tweede rij, eerste kolom, wilt gebruiken, markeert u de vijf termen in de tweede rij en de eerste kolom. De overige vier termen zijn de bijbehorende kleinere matrix.
- Zoek de determinant van elke minder belangrijke matrix door de diagonalen kruiselings te vermenigvuldigen en af te trekken, zoals weergegeven.
- Zie De basisbeginselen van matrices begrijpen voor meer informatie over minder belangrijke matrices en hun gebruik.
-
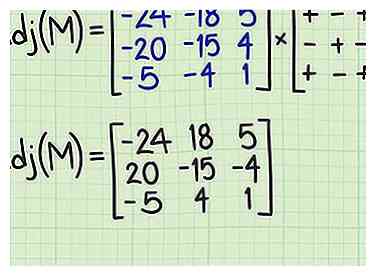 4 Maak de matrix van cofactoren. Plaats de resultaten van de vorige stap in een nieuwe matrix van cofactoren door elke minder belangrijke matrixdeterminant uit te lijnen met de overeenkomstige positie in de originele matrix. Dus de determinant die u hebt berekend op basis van item (1,1) van de originele matrix, gaat in positie (1,1). Vervolgens moet u het teken van afwisselende termen van deze nieuwe matrix omkeren volgens het weergegeven "dambordpatroon".[4]
4 Maak de matrix van cofactoren. Plaats de resultaten van de vorige stap in een nieuwe matrix van cofactoren door elke minder belangrijke matrixdeterminant uit te lijnen met de overeenkomstige positie in de originele matrix. Dus de determinant die u hebt berekend op basis van item (1,1) van de originele matrix, gaat in positie (1,1). Vervolgens moet u het teken van afwisselende termen van deze nieuwe matrix omkeren volgens het weergegeven "dambordpatroon".[4] - Bij het toekennen van tekens behoudt het eerste element van de eerste rij zijn oorspronkelijke teken. Het tweede element is omgekeerd. Het derde element behoudt zijn oorspronkelijke teken. Ga op deze manier door met de rest van de matrix. Merk op dat de (+) of (-) tekens in het damborddiagram niet suggereren dat de laatste term positief of negatief moet zijn. Het zijn indicatoren voor het behouden (+) of omkeren (-) van welk teken dan ook oorspronkelijk.
- Zie Understand the Basics of Matrices voor een bespreking van cofactoren.
- Het eindresultaat van deze stap wordt de adjugaatmatrix van het origineel genoemd. Dit wordt soms de adjoint-matrix genoemd. De toegevoegde matrix wordt genoteerd als Adj (M).
-
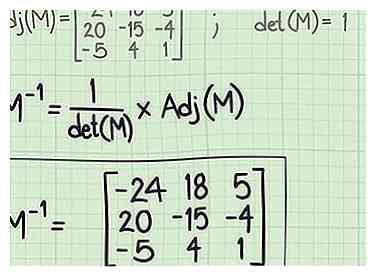 5 Verdeel elke term van de toegevoegde matrix door de determinant. Herinner de determinant van M die u in de eerste stap hebt berekend (om te controleren of de inverse mogelijk was). Je deelt nu elke term van de matrix met die waarde. Plaats het resultaat van elke berekening op de plek van de oorspronkelijke term. Het resultaat is het omgekeerde van de originele matrix.[5]
5 Verdeel elke term van de toegevoegde matrix door de determinant. Herinner de determinant van M die u in de eerste stap hebt berekend (om te controleren of de inverse mogelijk was). Je deelt nu elke term van de matrix met die waarde. Plaats het resultaat van elke berekening op de plek van de oorspronkelijke term. Het resultaat is het omgekeerde van de originele matrix.[5] - Voor de monstermatrix die in het diagram wordt getoond, is de bepalende factor 1. Daarom resulteert het verdelen van elke term van de toegevoegde matrix in de complementaire matrix zelf. (Je zult niet altijd zoveel geluk hebben.)
- In plaats van te delen, vertegenwoordigen sommige bronnen deze stap door elke term van M te vermenigvuldigen met 1 / det (M). Wiskundig gezien zijn deze gelijkwaardig.
Methode twee van drie:
Gebruik van lineaire rijreductie om de inverse matrix te vinden
-
 1 Verbind de identiteitsmatrix met de originele matrix. Schrijf de originele matrix M weg, teken een verticale lijn rechts ervan en schrijf vervolgens de identiteitsmatrix rechts ervan. Je zou nu moeten hebben wat een matrix lijkt te zijn met elk drie rijen van zes kolommen.[6]
1 Verbind de identiteitsmatrix met de originele matrix. Schrijf de originele matrix M weg, teken een verticale lijn rechts ervan en schrijf vervolgens de identiteitsmatrix rechts ervan. Je zou nu moeten hebben wat een matrix lijkt te zijn met elk drie rijen van zes kolommen.[6] - Bedenk dat de identiteitsmatrix een speciale matrix is met 1 s in elke positie van de hoofddiagonaal van linksboven naar rechtsonder en 0s in alle andere posities. Zie De basisbeginselen van matrices begrijpen voor een beoordeling van de identiteitsmatrix en de bijbehorende eigenschappen.
-
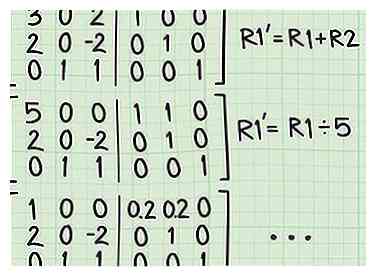 2 Voer lineaire rijreductiewerkzaamheden uit. Uw doel is om de identiteitsmatrix aan de linkerkant van deze nieuwe augmented matrix te maken. Terwijl u rijenverlagingsstappen aan de linkerkant uitvoert, moet u consequent dezelfde bewerkingen rechts uitvoeren, die zijn begonnen als uw identiteitsmatrix.[7]
2 Voer lineaire rijreductiewerkzaamheden uit. Uw doel is om de identiteitsmatrix aan de linkerkant van deze nieuwe augmented matrix te maken. Terwijl u rijenverlagingsstappen aan de linkerkant uitvoert, moet u consequent dezelfde bewerkingen rechts uitvoeren, die zijn begonnen als uw identiteitsmatrix.[7] - Vergeet niet dat rijverlagingen worden uitgevoerd als een combinatie van scalaire vermenigvuldiging en rijtoevoeging of -aftrekking, om afzonderlijke termen van de matrix te isoleren. Zie rij-matrices voor een vollediger beoordeling.
-
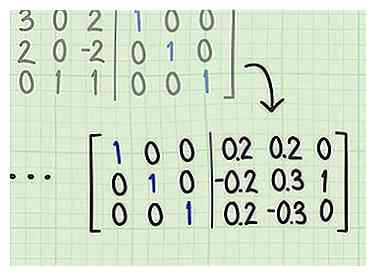 3 Ga door totdat je de identiteitsmatrix vormt. Blijf lineaire rijverkortingsbewerkingen herhalen totdat de linkerkant van uw augmented matrix de identiteitsmatrix weergeeft (diagonaal van 1s, met andere termen 0). Wanneer u dit punt hebt bereikt, is de rechterkant van uw verticale scheidingslijn het omgekeerde van uw oorspronkelijke matrix.[8]
3 Ga door totdat je de identiteitsmatrix vormt. Blijf lineaire rijverkortingsbewerkingen herhalen totdat de linkerkant van uw augmented matrix de identiteitsmatrix weergeeft (diagonaal van 1s, met andere termen 0). Wanneer u dit punt hebt bereikt, is de rechterkant van uw verticale scheidingslijn het omgekeerde van uw oorspronkelijke matrix.[8] -
 4 Schrijf de inverse matrix uit. Kopieer de elementen die nu aan de rechterkant van de verticale verdeler verschijnen als de inverse matrix.[9]
4 Schrijf de inverse matrix uit. Kopieer de elementen die nu aan de rechterkant van de verticale verdeler verschijnen als de inverse matrix.[9]
Methode drie van drie:
Gebruik een rekenmachine om de inverse matrix te vinden
-
 1 Selecteer een rekenmachine met matrixmogelijkheden. Eenvoudige rekenmachines met 4 functies kunnen u niet helpen om direct het omgekeerde te vinden. Vanwege de repetitieve aard van de berekeningen kan een geavanceerde grafische rekenmachine, zoals de Texas Instruments TI-83 of TI-86, het werk aanzienlijk verminderen.[10]
1 Selecteer een rekenmachine met matrixmogelijkheden. Eenvoudige rekenmachines met 4 functies kunnen u niet helpen om direct het omgekeerde te vinden. Vanwege de repetitieve aard van de berekeningen kan een geavanceerde grafische rekenmachine, zoals de Texas Instruments TI-83 of TI-86, het werk aanzienlijk verminderen.[10] -
 2 Voer je matrix in de rekenmachine in. Voer eerst de Matrix-functie van uw rekenmachine in door op de Matrix-toets te drukken, als u die hebt. Op de rekenmachines van Texas Instruments moet u mogelijk op 2 drukkennd Matrix.
2 Voer je matrix in de rekenmachine in. Voer eerst de Matrix-functie van uw rekenmachine in door op de Matrix-toets te drukken, als u die hebt. Op de rekenmachines van Texas Instruments moet u mogelijk op 2 drukkennd Matrix. -
 3 Selecteer het submenu Bewerken. Om het submenu te bereiken, moet u mogelijk de pijlknoppen gebruiken of de juiste functietoets boven aan het toetsenbord van uw rekenmachine kiezen, afhankelijk van de indeling van uw rekenmachine.[11]
3 Selecteer het submenu Bewerken. Om het submenu te bereiken, moet u mogelijk de pijlknoppen gebruiken of de juiste functietoets boven aan het toetsenbord van uw rekenmachine kiezen, afhankelijk van de indeling van uw rekenmachine.[11] -
 4 Selecteer een naam voor uw matrix. De meeste rekenmachines zijn uitgerust om te werken met overal van 3 tot 10 matrices, gelabeld met letters A tot en met J. Gewoonlijk kiest u [A] om mee te werken. Druk op de Enter-toets nadat je je selectie hebt gemaakt.[12]
4 Selecteer een naam voor uw matrix. De meeste rekenmachines zijn uitgerust om te werken met overal van 3 tot 10 matrices, gelabeld met letters A tot en met J. Gewoonlijk kiest u [A] om mee te werken. Druk op de Enter-toets nadat je je selectie hebt gemaakt.[12] -
 5 Voer de afmetingen van uw matrix in. Dit artikel concentreert zich op 3x3-matrices. De rekenmachine kan echter grotere formaten aan. Voer het aantal rijen in en druk vervolgens op Enter en vervolgens op het aantal kolommen en op Enter.[13]
5 Voer de afmetingen van uw matrix in. Dit artikel concentreert zich op 3x3-matrices. De rekenmachine kan echter grotere formaten aan. Voer het aantal rijen in en druk vervolgens op Enter en vervolgens op het aantal kolommen en op Enter.[13] -
 6 Voer elk element van de matrix in. Het calculatorscherm toont een matrix. Als u eerder met de matrixfunctie werkte, wordt de vorige matrix op het scherm weergegeven. De cursor markeert het eerste element van de matrix. Typ de waarde in van de matrix die u wilt oplossen en druk op Enter. De cursor gaat automatisch naar het volgende element van de matrix en overschrijft eventuele eerdere nummers.[14]
6 Voer elk element van de matrix in. Het calculatorscherm toont een matrix. Als u eerder met de matrixfunctie werkte, wordt de vorige matrix op het scherm weergegeven. De cursor markeert het eerste element van de matrix. Typ de waarde in van de matrix die u wilt oplossen en druk op Enter. De cursor gaat automatisch naar het volgende element van de matrix en overschrijft eventuele eerdere nummers.[14] - Als u een negatief getal wilt invoeren, gebruikt u de negatieve knop van de rekenmachine (-) en niet de mintoets. De matrixfunctie zal het nummer niet goed lezen.
- Indien nodig kunt u de pijltoetsen van uw rekenmachine gebruiken om door de matrix te springen.
-
 7 Sluit de Matrix-functie. Nadat u alle waarden van de matrix hebt ingevoerd, drukt u op de toets Afsluiten (of 2nd Sluit, indien nodig). Hiermee verlaat u de Matrix-functie en keert u terug naar het hoofdscherm van uw rekenmachine.[15]
7 Sluit de Matrix-functie. Nadat u alle waarden van de matrix hebt ingevoerd, drukt u op de toets Afsluiten (of 2nd Sluit, indien nodig). Hiermee verlaat u de Matrix-functie en keert u terug naar het hoofdscherm van uw rekenmachine.[15] -
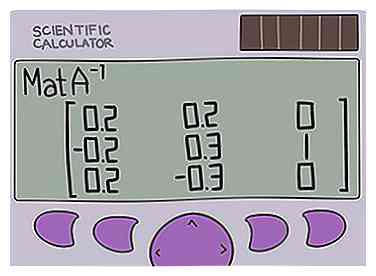 8 Gebruik de inverse toets om de inverse matrix te vinden. Open eerst de Matrix-functie opnieuw en gebruik de knop Namen om het matrixlabel te selecteren dat u hebt gebruikt om uw matrix te definiëren (waarschijnlijk [A]). Druk vervolgens op de inverse toets van uw rekenmachine, . Dit kan het gebruik van de 2 vereisennd knop, afhankelijk van uw rekenmachine. Uw scherm moet verschijnen . Druk op Enter en de inverse matrix zou op uw scherm moeten verschijnen.[16]
8 Gebruik de inverse toets om de inverse matrix te vinden. Open eerst de Matrix-functie opnieuw en gebruik de knop Namen om het matrixlabel te selecteren dat u hebt gebruikt om uw matrix te definiëren (waarschijnlijk [A]). Druk vervolgens op de inverse toets van uw rekenmachine, . Dit kan het gebruik van de 2 vereisennd knop, afhankelijk van uw rekenmachine. Uw scherm moet verschijnen . Druk op Enter en de inverse matrix zou op uw scherm moeten verschijnen.[16] - Gebruik de ^ -knop op uw rekenmachine niet om te proberen A ^ -1 in te voeren als afzonderlijke toetsaanslagen. De calculator begrijpt deze bewerking niet.
- Als u een foutmelding ontvangt wanneer u de inverse sleutel invoert, is de kans groot dat uw oorspronkelijke matrix geen inverse heeft. Misschien wil je teruggaan en de determinant berekenen om uit te vinden.
-
 9 Converteer uw inverse matrix naar exacte antwoorden. De eerste berekening die de rekenmachine u zal geven is in decimale vorm. Dit wordt voor de meeste doeleinden niet als "exact" beschouwd. U moet de decimale antwoorden naar een fractioneel formulier converteren, indien nodig. (Als u veel geluk heeft, zijn al uw resultaten gehele getallen, maar dit is zeldzaam.)[17]
9 Converteer uw inverse matrix naar exacte antwoorden. De eerste berekening die de rekenmachine u zal geven is in decimale vorm. Dit wordt voor de meeste doeleinden niet als "exact" beschouwd. U moet de decimale antwoorden naar een fractioneel formulier converteren, indien nodig. (Als u veel geluk heeft, zijn al uw resultaten gehele getallen, maar dit is zeldzaam.)[17] - Uw rekenmachine heeft waarschijnlijk een functie die de decimalen automatisch omzet in breuken. Gebruik bijvoorbeeld de TI-86, voer de wiskundige functie in en selecteer vervolgens Misc en vervolgens Frac en Enter. De decimalen worden automatisch als breuken weergegeven.
- 10 De meeste grafische rekenmachines hebben ook vierkante haakjes toetsen (op TI-84 is het 2e + x en 2e + -) die kunnen worden gebruikt om een matrix in te typen zonder de matrixfunctie te gebruiken. Opmerking: de rekenmachine zal de matrix niet formatteren tot nadat de toets enter / equals is gebruikt (dat wil zeggen dat alles één regel is en niet mooi).
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Controleer de determinant van de matrix. U moet de determinant van de matrix als een eerste stap berekenen. Als de determinant 0 is, is uw werk voltooid, omdat de matrix geen inverse heeft. De determinant van matrix M kan symbolisch worden weergegeven als det (M).[1]
1 Controleer de determinant van de matrix. U moet de determinant van de matrix als een eerste stap berekenen. Als de determinant 0 is, is uw werk voltooid, omdat de matrix geen inverse heeft. De determinant van matrix M kan symbolisch worden weergegeven als det (M).[1]  2 Transponeer de originele matrix. Transposeriemiddelen die de matrix om de hoofddiagonaal weergeven, of equivalent, het (i, j) ste element en het (j, i) ste omwisselen. Wanneer u de termen van de matrix transponeert, zou u moeten zien dat de hoofddiagonaal (van linksboven naar rechtsonder) ongewijzigd is.[2]
2 Transponeer de originele matrix. Transposeriemiddelen die de matrix om de hoofddiagonaal weergeven, of equivalent, het (i, j) ste element en het (j, i) ste omwisselen. Wanneer u de termen van de matrix transponeert, zou u moeten zien dat de hoofddiagonaal (van linksboven naar rechtsonder) ongewijzigd is.[2]  3 Zoek de determinant van elk van de 2x2 minor matrices. Elk item van de nieuw getransponeerde 3x3-matrix is gekoppeld aan een overeenkomstige 2x2 "ondergeschikte" matrix. Om de juiste kleine matrix voor elke term te vinden, markeert u eerst de rij en kolom van de term waarmee u begint. Dit moet vijf termen van de matrix bevatten. De overige vier termen vormen de secundaire matrix.[3]
3 Zoek de determinant van elk van de 2x2 minor matrices. Elk item van de nieuw getransponeerde 3x3-matrix is gekoppeld aan een overeenkomstige 2x2 "ondergeschikte" matrix. Om de juiste kleine matrix voor elke term te vinden, markeert u eerst de rij en kolom van de term waarmee u begint. Dit moet vijf termen van de matrix bevatten. De overige vier termen vormen de secundaire matrix.[3] 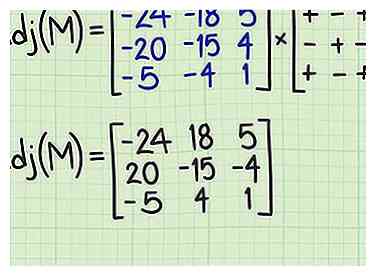 4 Maak de matrix van cofactoren. Plaats de resultaten van de vorige stap in een nieuwe matrix van cofactoren door elke minder belangrijke matrixdeterminant uit te lijnen met de overeenkomstige positie in de originele matrix. Dus de determinant die u hebt berekend op basis van item (1,1) van de originele matrix, gaat in positie (1,1). Vervolgens moet u het teken van afwisselende termen van deze nieuwe matrix omkeren volgens het weergegeven "dambordpatroon".[4]
4 Maak de matrix van cofactoren. Plaats de resultaten van de vorige stap in een nieuwe matrix van cofactoren door elke minder belangrijke matrixdeterminant uit te lijnen met de overeenkomstige positie in de originele matrix. Dus de determinant die u hebt berekend op basis van item (1,1) van de originele matrix, gaat in positie (1,1). Vervolgens moet u het teken van afwisselende termen van deze nieuwe matrix omkeren volgens het weergegeven "dambordpatroon".[4] 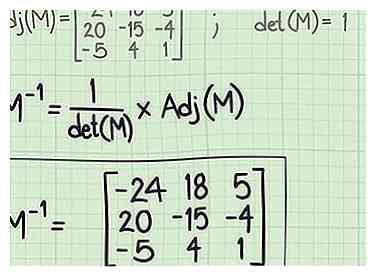 5 Verdeel elke term van de toegevoegde matrix door de determinant. Herinner de determinant van M die u in de eerste stap hebt berekend (om te controleren of de inverse mogelijk was). Je deelt nu elke term van de matrix met die waarde. Plaats het resultaat van elke berekening op de plek van de oorspronkelijke term. Het resultaat is het omgekeerde van de originele matrix.[5]
5 Verdeel elke term van de toegevoegde matrix door de determinant. Herinner de determinant van M die u in de eerste stap hebt berekend (om te controleren of de inverse mogelijk was). Je deelt nu elke term van de matrix met die waarde. Plaats het resultaat van elke berekening op de plek van de oorspronkelijke term. Het resultaat is het omgekeerde van de originele matrix.[5]  1 Verbind de identiteitsmatrix met de originele matrix. Schrijf de originele matrix M weg, teken een verticale lijn rechts ervan en schrijf vervolgens de identiteitsmatrix rechts ervan. Je zou nu moeten hebben wat een matrix lijkt te zijn met elk drie rijen van zes kolommen.[6]
1 Verbind de identiteitsmatrix met de originele matrix. Schrijf de originele matrix M weg, teken een verticale lijn rechts ervan en schrijf vervolgens de identiteitsmatrix rechts ervan. Je zou nu moeten hebben wat een matrix lijkt te zijn met elk drie rijen van zes kolommen.[6]  2 Voer lineaire rijreductiewerkzaamheden uit. Uw doel is om de identiteitsmatrix aan de linkerkant van deze nieuwe augmented matrix te maken. Terwijl u rijenverlagingsstappen aan de linkerkant uitvoert, moet u consequent dezelfde bewerkingen rechts uitvoeren, die zijn begonnen als uw identiteitsmatrix.[7]
2 Voer lineaire rijreductiewerkzaamheden uit. Uw doel is om de identiteitsmatrix aan de linkerkant van deze nieuwe augmented matrix te maken. Terwijl u rijenverlagingsstappen aan de linkerkant uitvoert, moet u consequent dezelfde bewerkingen rechts uitvoeren, die zijn begonnen als uw identiteitsmatrix.[7]  3 Ga door totdat je de identiteitsmatrix vormt. Blijf lineaire rijverkortingsbewerkingen herhalen totdat de linkerkant van uw augmented matrix de identiteitsmatrix weergeeft (diagonaal van 1s, met andere termen 0). Wanneer u dit punt hebt bereikt, is de rechterkant van uw verticale scheidingslijn het omgekeerde van uw oorspronkelijke matrix.[8]
3 Ga door totdat je de identiteitsmatrix vormt. Blijf lineaire rijverkortingsbewerkingen herhalen totdat de linkerkant van uw augmented matrix de identiteitsmatrix weergeeft (diagonaal van 1s, met andere termen 0). Wanneer u dit punt hebt bereikt, is de rechterkant van uw verticale scheidingslijn het omgekeerde van uw oorspronkelijke matrix.[8]  4 Schrijf de inverse matrix uit. Kopieer de elementen die nu aan de rechterkant van de verticale verdeler verschijnen als de inverse matrix.[9]
4 Schrijf de inverse matrix uit. Kopieer de elementen die nu aan de rechterkant van de verticale verdeler verschijnen als de inverse matrix.[9]  1 Selecteer een rekenmachine met matrixmogelijkheden. Eenvoudige rekenmachines met 4 functies kunnen u niet helpen om direct het omgekeerde te vinden. Vanwege de repetitieve aard van de berekeningen kan een geavanceerde grafische rekenmachine, zoals de Texas Instruments TI-83 of TI-86, het werk aanzienlijk verminderen.[10]
1 Selecteer een rekenmachine met matrixmogelijkheden. Eenvoudige rekenmachines met 4 functies kunnen u niet helpen om direct het omgekeerde te vinden. Vanwege de repetitieve aard van de berekeningen kan een geavanceerde grafische rekenmachine, zoals de Texas Instruments TI-83 of TI-86, het werk aanzienlijk verminderen.[10]  2 Voer je matrix in de rekenmachine in. Voer eerst de Matrix-functie van uw rekenmachine in door op de Matrix-toets te drukken, als u die hebt. Op de rekenmachines van Texas Instruments moet u mogelijk op 2 drukkennd Matrix.
2 Voer je matrix in de rekenmachine in. Voer eerst de Matrix-functie van uw rekenmachine in door op de Matrix-toets te drukken, als u die hebt. Op de rekenmachines van Texas Instruments moet u mogelijk op 2 drukkennd Matrix.  3 Selecteer het submenu Bewerken. Om het submenu te bereiken, moet u mogelijk de pijlknoppen gebruiken of de juiste functietoets boven aan het toetsenbord van uw rekenmachine kiezen, afhankelijk van de indeling van uw rekenmachine.[11]
3 Selecteer het submenu Bewerken. Om het submenu te bereiken, moet u mogelijk de pijlknoppen gebruiken of de juiste functietoets boven aan het toetsenbord van uw rekenmachine kiezen, afhankelijk van de indeling van uw rekenmachine.[11]  4 Selecteer een naam voor uw matrix. De meeste rekenmachines zijn uitgerust om te werken met overal van 3 tot 10 matrices, gelabeld met letters A tot en met J. Gewoonlijk kiest u [A] om mee te werken. Druk op de Enter-toets nadat je je selectie hebt gemaakt.[12]
4 Selecteer een naam voor uw matrix. De meeste rekenmachines zijn uitgerust om te werken met overal van 3 tot 10 matrices, gelabeld met letters A tot en met J. Gewoonlijk kiest u [A] om mee te werken. Druk op de Enter-toets nadat je je selectie hebt gemaakt.[12]  5 Voer de afmetingen van uw matrix in. Dit artikel concentreert zich op 3x3-matrices. De rekenmachine kan echter grotere formaten aan. Voer het aantal rijen in en druk vervolgens op Enter en vervolgens op het aantal kolommen en op Enter.[13]
5 Voer de afmetingen van uw matrix in. Dit artikel concentreert zich op 3x3-matrices. De rekenmachine kan echter grotere formaten aan. Voer het aantal rijen in en druk vervolgens op Enter en vervolgens op het aantal kolommen en op Enter.[13]  6 Voer elk element van de matrix in. Het calculatorscherm toont een matrix. Als u eerder met de matrixfunctie werkte, wordt de vorige matrix op het scherm weergegeven. De cursor markeert het eerste element van de matrix. Typ de waarde in van de matrix die u wilt oplossen en druk op Enter. De cursor gaat automatisch naar het volgende element van de matrix en overschrijft eventuele eerdere nummers.[14]
6 Voer elk element van de matrix in. Het calculatorscherm toont een matrix. Als u eerder met de matrixfunctie werkte, wordt de vorige matrix op het scherm weergegeven. De cursor markeert het eerste element van de matrix. Typ de waarde in van de matrix die u wilt oplossen en druk op Enter. De cursor gaat automatisch naar het volgende element van de matrix en overschrijft eventuele eerdere nummers.[14]  7 Sluit de Matrix-functie. Nadat u alle waarden van de matrix hebt ingevoerd, drukt u op de toets Afsluiten (of 2nd Sluit, indien nodig). Hiermee verlaat u de Matrix-functie en keert u terug naar het hoofdscherm van uw rekenmachine.[15]
7 Sluit de Matrix-functie. Nadat u alle waarden van de matrix hebt ingevoerd, drukt u op de toets Afsluiten (of 2nd Sluit, indien nodig). Hiermee verlaat u de Matrix-functie en keert u terug naar het hoofdscherm van uw rekenmachine.[15]  8 Gebruik de inverse toets om de inverse matrix te vinden. Open eerst de Matrix-functie opnieuw en gebruik de knop Namen om het matrixlabel te selecteren dat u hebt gebruikt om uw matrix te definiëren (waarschijnlijk [A]). Druk vervolgens op de inverse toets van uw rekenmachine,
8 Gebruik de inverse toets om de inverse matrix te vinden. Open eerst de Matrix-functie opnieuw en gebruik de knop Namen om het matrixlabel te selecteren dat u hebt gebruikt om uw matrix te definiëren (waarschijnlijk [A]). Druk vervolgens op de inverse toets van uw rekenmachine,  9 Converteer uw inverse matrix naar exacte antwoorden. De eerste berekening die de rekenmachine u zal geven is in decimale vorm. Dit wordt voor de meeste doeleinden niet als "exact" beschouwd. U moet de decimale antwoorden naar een fractioneel formulier converteren, indien nodig. (Als u veel geluk heeft, zijn al uw resultaten gehele getallen, maar dit is zeldzaam.)[17]
9 Converteer uw inverse matrix naar exacte antwoorden. De eerste berekening die de rekenmachine u zal geven is in decimale vorm. Dit wordt voor de meeste doeleinden niet als "exact" beschouwd. U moet de decimale antwoorden naar een fractioneel formulier converteren, indien nodig. (Als u veel geluk heeft, zijn al uw resultaten gehele getallen, maar dit is zeldzaam.)[17]