Het vermenigvuldigen van breuken is een van de basisvaardigheden die iedereen die te maken heeft met breuken moet kennen. Om breuken te vermenigvuldigen, hoef je alleen maar hun tellers en de noemers te vermenigvuldigen, en dan je antwoord te vereenvoudigen als je kunt. Met een beetje oefening kan iedereen breuken vermenigvuldigen als een professionele wiskundige.
Methode één van de twee:
Vermenigvuldigen voor het vereenvoudigen
-
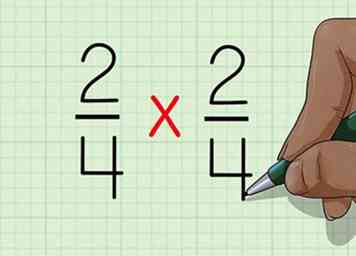 1 Schrijf het probleem op. De twee breuken moeten worden genoteerd zodat hun tellers zijn uitgelijnd met hun noemers.
1 Schrijf het probleem op. De twee breuken moeten worden genoteerd zodat hun tellers zijn uitgelijnd met hun noemers. - Vb: 2/4 * 2/4
-
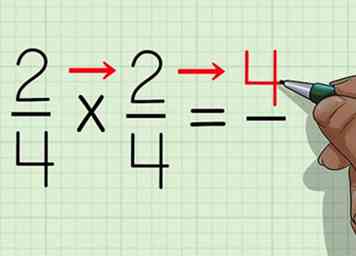 2 Vermenigvuldig de tellers van de twee breuken. Omdat de tellers beide 2 zijn, kun je 2 * 2 vermenigvuldigen om 4 te krijgen.
2 Vermenigvuldig de tellers van de twee breuken. Omdat de tellers beide 2 zijn, kun je 2 * 2 vermenigvuldigen om 4 te krijgen. -
 3 Vermenigvuldig de noemers van de twee breuken. Omdat de noemers beide 4 zijn, vermenigvuldig 4 * 4 om 16 te krijgen.
3 Vermenigvuldig de noemers van de twee breuken. Omdat de noemers beide 4 zijn, vermenigvuldig 4 * 4 om 16 te krijgen. - Uw antwoord is een breuk die bestaat uit de nieuwe teller en de nieuwe noemer. Uw antwoord is 4/16.
-
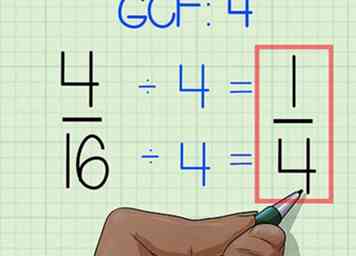 4 Makkelijker maken. Om een breuk te vereenvoudigen, moet u de teller en noemer delen door het grootste getal dat gelijkmatig in beide getallen kan worden ingevoerd. In het geval van 4/16 is 4 het grootste getal dat gelijk in beide getallen valt, dus deel de teller en de noemer met 4. Doe het als volgt:
4 Makkelijker maken. Om een breuk te vereenvoudigen, moet u de teller en noemer delen door het grootste getal dat gelijkmatig in beide getallen kan worden ingevoerd. In het geval van 4/16 is 4 het grootste getal dat gelijk in beide getallen valt, dus deel de teller en de noemer met 4. Doe het als volgt: - 4/4 = 1
- 16/4 = 4
- Je nieuwe breuk en het uiteindelijke antwoord is 1/4.
Methode twee van twee:
Vereenvoudig voor het vermenigvuldigen
-
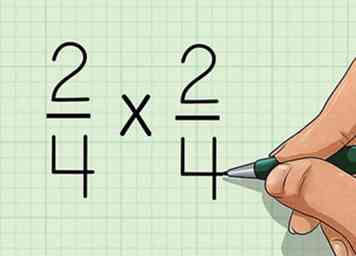 1 Schrijf het probleem op. De tellers en noemers van de twee breuken moeten worden uitgelijnd.
1 Schrijf het probleem op. De tellers en noemers van de twee breuken moeten worden uitgelijnd. - Vb: 2/4 * 2/4
-
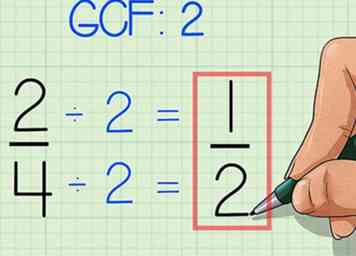 2 Vereenvoudig de eerste breuk. Om de eerste breuk te vereenvoudigen, 2/4, deelt u eenvoudig de teller en de noemer door het grootste getal dat in elk getal kan gaan. Omdat het grootste aantal dat in zowel 2 als 4 gaat 2 is, moet je zowel 2 als 4 delen door 2. Hier is hoe het te doen:
2 Vereenvoudig de eerste breuk. Om de eerste breuk te vereenvoudigen, 2/4, deelt u eenvoudig de teller en de noemer door het grootste getal dat in elk getal kan gaan. Omdat het grootste aantal dat in zowel 2 als 4 gaat 2 is, moet je zowel 2 als 4 delen door 2. Hier is hoe het te doen: - 2/2 = 1
- 4/2 = 2
- Je nieuwe breuk is 1/2. Het is een equivalent deel van 2/4, wat betekent dat het dezelfde waarde heeft.
- U kunt ook het grootste getal vinden dat zich in zowel de teller als de noemer verdeelt door de grootste gemene deler (GCF) van beide getallen te vinden. Hiertoe geeft u eenvoudig alle factoren van die getallen op en kiest u de grootste van beide. Hier is hoe:
- 2: 1, 2.
- 4: 1, 2, 4.
- 2 is het grootste getal dat in zowel 2 als 4 is verdeeld.
-
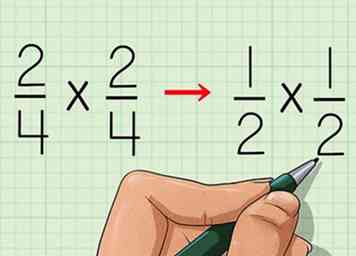 3 Vereenvoudig de tweede breuk. Om het proces te voltooien, moet u zowel de tweede als de eerste vereenvoudigen. Aangezien de tweede fractie, 2/4, hetzelfde is als de eerste, is uw antwoord hetzelfde.
3 Vereenvoudig de tweede breuk. Om het proces te voltooien, moet u zowel de tweede als de eerste vereenvoudigen. Aangezien de tweede fractie, 2/4, hetzelfde is als de eerste, is uw antwoord hetzelfde. - 2/4 = 1/2
-
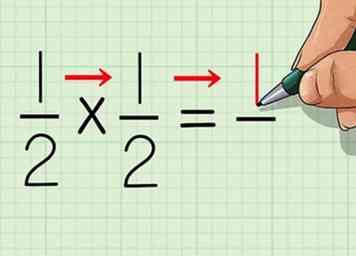 4 Vermenigvuldig de tellers van beide breuken. Vermenigvuldig de tellers van de breuken 1/2 en 1/2, die 1 en 1 zijn.
4 Vermenigvuldig de tellers van beide breuken. Vermenigvuldig de tellers van de breuken 1/2 en 1/2, die 1 en 1 zijn. - 1 * 1 = 1.
-
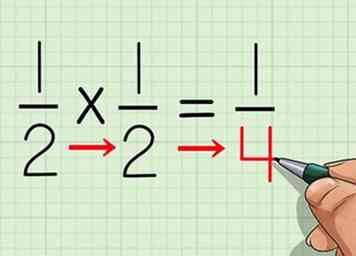 5 Vermenigvuldig de noemers van beide breuken. Vermenigvuldig de noemers van de breuken 1/2 en 1/2, die 2 en 2 zijn.
5 Vermenigvuldig de noemers van beide breuken. Vermenigvuldig de noemers van de breuken 1/2 en 1/2, die 2 en 2 zijn. - 2 * 2 = 4.
-
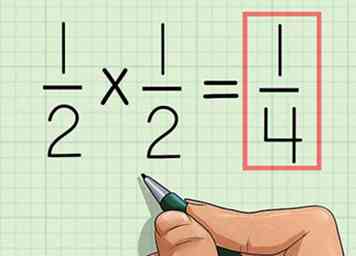 6 Plaats de nieuwe teller boven de nieuwe noemer. Omdat je aan het begin van het probleem al vereenvoudigd bent, heb je je laatste antwoord gevonden.
6 Plaats de nieuwe teller boven de nieuwe noemer. Omdat je aan het begin van het probleem al vereenvoudigd bent, heb je je laatste antwoord gevonden. - 1/2 * 1/2 = 1/4.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
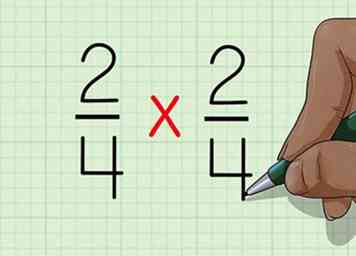 1 Schrijf het probleem op. De twee breuken moeten worden genoteerd zodat hun tellers zijn uitgelijnd met hun noemers.
1 Schrijf het probleem op. De twee breuken moeten worden genoteerd zodat hun tellers zijn uitgelijnd met hun noemers. 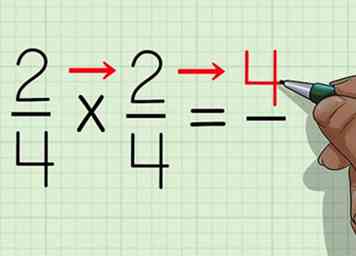 2 Vermenigvuldig de tellers van de twee breuken. Omdat de tellers beide 2 zijn, kun je 2 * 2 vermenigvuldigen om 4 te krijgen.
2 Vermenigvuldig de tellers van de twee breuken. Omdat de tellers beide 2 zijn, kun je 2 * 2 vermenigvuldigen om 4 te krijgen.  3 Vermenigvuldig de noemers van de twee breuken. Omdat de noemers beide 4 zijn, vermenigvuldig 4 * 4 om 16 te krijgen.
3 Vermenigvuldig de noemers van de twee breuken. Omdat de noemers beide 4 zijn, vermenigvuldig 4 * 4 om 16 te krijgen. 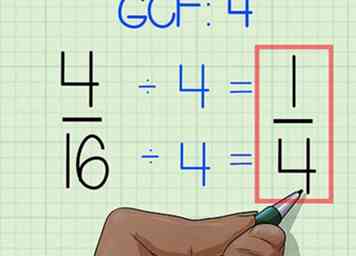 4 Makkelijker maken. Om een breuk te vereenvoudigen, moet u de teller en noemer delen door het grootste getal dat gelijkmatig in beide getallen kan worden ingevoerd. In het geval van 4/16 is 4 het grootste getal dat gelijk in beide getallen valt, dus deel de teller en de noemer met 4. Doe het als volgt:
4 Makkelijker maken. Om een breuk te vereenvoudigen, moet u de teller en noemer delen door het grootste getal dat gelijkmatig in beide getallen kan worden ingevoerd. In het geval van 4/16 is 4 het grootste getal dat gelijk in beide getallen valt, dus deel de teller en de noemer met 4. Doe het als volgt: 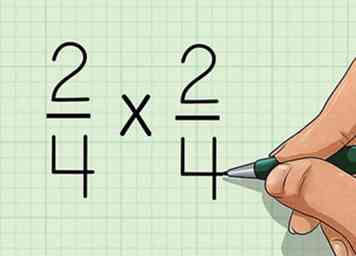 1 Schrijf het probleem op. De tellers en noemers van de twee breuken moeten worden uitgelijnd.
1 Schrijf het probleem op. De tellers en noemers van de twee breuken moeten worden uitgelijnd. 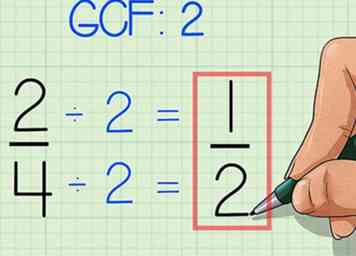 2 Vereenvoudig de eerste breuk. Om de eerste breuk te vereenvoudigen, 2/4, deelt u eenvoudig de teller en de noemer door het grootste getal dat in elk getal kan gaan. Omdat het grootste aantal dat in zowel 2 als 4 gaat 2 is, moet je zowel 2 als 4 delen door 2. Hier is hoe het te doen:
2 Vereenvoudig de eerste breuk. Om de eerste breuk te vereenvoudigen, 2/4, deelt u eenvoudig de teller en de noemer door het grootste getal dat in elk getal kan gaan. Omdat het grootste aantal dat in zowel 2 als 4 gaat 2 is, moet je zowel 2 als 4 delen door 2. Hier is hoe het te doen: 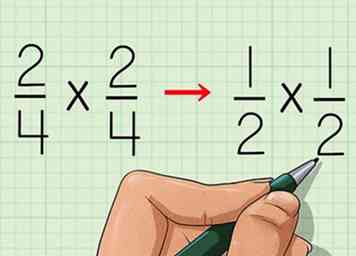 3 Vereenvoudig de tweede breuk. Om het proces te voltooien, moet u zowel de tweede als de eerste vereenvoudigen. Aangezien de tweede fractie, 2/4, hetzelfde is als de eerste, is uw antwoord hetzelfde.
3 Vereenvoudig de tweede breuk. Om het proces te voltooien, moet u zowel de tweede als de eerste vereenvoudigen. Aangezien de tweede fractie, 2/4, hetzelfde is als de eerste, is uw antwoord hetzelfde. 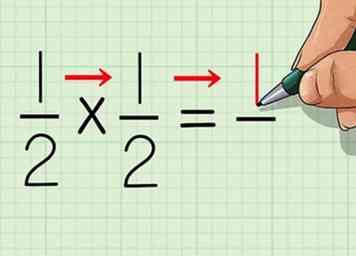 4 Vermenigvuldig de tellers van beide breuken. Vermenigvuldig de tellers van de breuken 1/2 en 1/2, die 1 en 1 zijn.
4 Vermenigvuldig de tellers van beide breuken. Vermenigvuldig de tellers van de breuken 1/2 en 1/2, die 1 en 1 zijn. 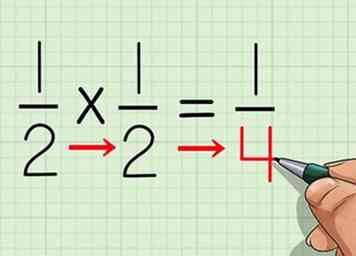 5 Vermenigvuldig de noemers van beide breuken. Vermenigvuldig de noemers van de breuken 1/2 en 1/2, die 2 en 2 zijn.
5 Vermenigvuldig de noemers van beide breuken. Vermenigvuldig de noemers van de breuken 1/2 en 1/2, die 2 en 2 zijn. 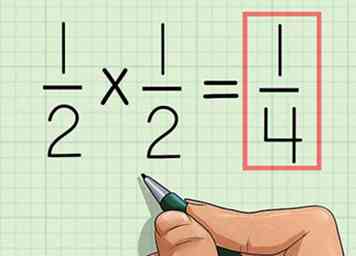 6 Plaats de nieuwe teller boven de nieuwe noemer. Omdat je aan het begin van het probleem al vereenvoudigd bent, heb je je laatste antwoord gevonden.
6 Plaats de nieuwe teller boven de nieuwe noemer. Omdat je aan het begin van het probleem al vereenvoudigd bent, heb je je laatste antwoord gevonden.