Het schatten van (of het maken van een gefundeerde schatting) kan erg nuttig zijn als het gaat om breuken. Als u bepaalde verhoudingen probeert te achterhalen zonder de gegevens of tijd te hebben om tot een nauwkeurig antwoord te komen, zal het maken van een juiste schatting u op de juiste weg zetten. Er is echter een fijn verschil tussen het maken van schattingen en raden uit de lucht. Als u uw kansen op nauwkeurigheid wilt maximaliseren, moet u uw gegevens zorgvuldig bekijken.

Methode één van de twee:
Fracties op mentale wijze schatten

  1. 1 Bepaal of een schatting geschikt is. Als u een breuk schat, krijgt u de kern van de breuk. U zult echter zelden het exacte antwoord ermee raden. Als u alleen een algemeen idee van het antwoord nodig hebt, zijn schattingen nuttig. Als u echter een exact antwoord wilt geven, moet u uw vergelijking oplossen met exacte metingen. Een goede schatting zal het algemene idee snel overbrengen en zal niet proberen zichzelf als een exact antwoord door te geven.
    • Voorbeelden van situaties die schattingen begunstigen, zijn het plannen van incidentele gebeurtenissen (ongeveer het meten van benodigdheden die nodig zijn), verbaal een idee uiten (het idee overbrengen zonder de details) of sommige kooksituaties zoals stoofschotels, waar exacte metingen niet nodig zijn in de finale artikel.
  2. 2 Vereenvoudig de breuken waar mogelijk.[1] Breuken zullen altijd gemakkelijker zijn om mentaal om te gaan als je ze simpelweg tot hun kleinste gemene delers maakt. Een fractie die wordt weergegeven als 4/8, bijvoorbeeld, kan worden uitgedrukt als 2/4 of 1/2. Dit zijn verschillende manieren om exact dezelfde fractie uit te drukken. Het is een goed idee om uw breuken te vereenvoudigen, maar mogelijk om uw schatting gemakkelijker te maken. Zoek een getal dat je gelijk kunt verdelen over de bovenste en onderste helft van een breuk. Als u ze op hetzelfde aantal verdeelt, wordt de grootte van de getallen kleiner, terwijl de verhoudingen intact blijven.
    • Kleinere nummers zijn over het algemeen gemakkelijker om mee te werken dan grote getallen. Als alle opgenomen nummers dezelfde gemene deler hebben, is het mogelijk om ze op basis van die wortel op te delen. Bijvoorbeeld, 4/16 en 6/8 kunnen worden gedeeld door respectievelijk 4 en 2. Dit zou resulteren in 1/4 en 3/4.[2]
    • Over het algemeen gesproken, als zowel de bovenkant als de onderkant van uw breuk even zijn, kunt u beide zijden met 2 delen. Beide zijden zijn slechts half zo groot als voorheen en de verhouding blijft hetzelfde.
    • Zorg ervoor dat je beide kanten van je breuk heel houdt terwijl je deelt. Het maken van breuken uit breuken door ongeldige noemers te splitsen, maakt je breuk veel frustrerender om mee om te gaan.
  3. 3 Rond de breuken.[3] Afrondingen maken het gemakkelijker om ermee om te gaan. Als u een breuk hebt die niet kan worden vereenvoudigd zoals deze is, kunt u deze vereenvoudigen ten koste van het "exacte" antwoord, door deze iets omhoog of omlaag te verplaatsen. Fracties omhoog of omlaag afronden, zal van veel dingen afhangen, met name of je te maken hebt met heel veel heel specifieke breuken, en of er nog maar weinig onderdelen zijn om nog zinvol te zijn.
    • "Afronden" van een breuk betekent het iets naar boven of naar beneden brengen, zodat de breuk vereenvoudigd kan worden. Bijvoorbeeld, 7/16 kan een lastige fractie zijn om mentaal te visualiseren, maar als je het een beetje afrondt naar 8/16, wordt het precies de helft (1/2) van het geheel.
  4. 4 Kies een geschikt aantal afrondingsopties. Als je mentale wiskunde wilt gebruiken, is het een goed idee om te proberen je breuken af ​​te ronden naar verhoudingen waarmee je het meest vertrouwd bent. Omdat persoonlijke vaardigheden met mentale wiskunde afhankelijk zijn van het individu, kun je de afronding zo groot of klein maken als je wilt. Afronden op helften (0, 1/2, 1) is alleen zinvol voor de eenvoudigste breuken, terwijl complexere verhoudingen zullen profiteren van een groter aantal afrondingsopties.
    • Afronding van uw breuken in kleinere porties (zoals achtste of zestiende) kan moeilijker zijn, afhankelijk van uw niveau, maar u zult merken dat uw antwoord dichter bij het echte antwoord ligt.[4]
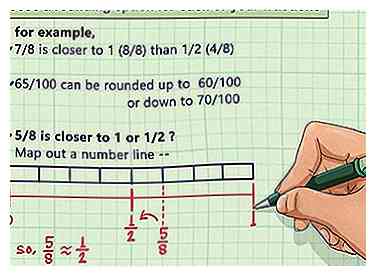  5. 5 Kies een afrondingsoptie voor elk van uw breuken. Meestal zal een fractie dichter bij een van de aangrenzende afrondingsopties zijn dan de andere. 7/8 is bijvoorbeeld dichter bij 1 (8/8) dan 1/2 (4/8). In sommige gevallen kan het echter ergens in het midden liggen. Een breuk zoals 65/100 kan naar boven of naar beneden worden afgerond naar 60/100 of 70/100. U kunt een beslissing nemen waarvan u denkt dat deze de gegeven gegevens het beste weergeeft. Het in kaart brengen van een getallenlijn helpt om visueel aan te geven welke afrondingsoptie een breuk het dichtst benadert.[5]
    • Hoewel het vanzelfsprekend kan zijn, hoeft u niets te doen aan breuken die al op een van uw afrondingsopties vallen.
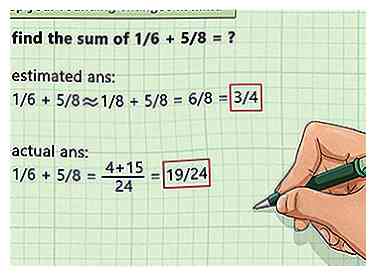  6. 6 Houd rekening met uw afrondingsveranderingen. Hoewel afrondingen naar boven en beneden nuttig kunnen zijn om te schatten, is het belangrijk dat u deze nieuwe verhoudingen niet als een nauwkeurig rapport van de werkelijke verhoudingen neemt.[6] Houd de originele, precieze breuken bij de hand. Het is handig om zowel de exacte als de geschatte versie beschikbaar te hebben, omdat u het idee gemakkelijk kunt communiceren en het kunt back-uppen met de harde gegevens wanneer dat nodig is.
  7. 7 Vergelijk uw schatting met de precieze breuken. Zodra u een afgeronde, vereenvoudigde schatting hebt waarmee u vertrouwd bent, kunt u uw schatting verder verfijnen door deze tegen de oorspronkelijke breuk aan te duwen. Op deze manier kunt u bepalen hoe uw schatting kan afwijken van het werkelijke aantal. Hoewel een schatting een goede manier is om de gegevens in grote lijnen te visualiseren of er ruim over na te denken, moet u nadenken over hoe dichtbij uw breuk eigenlijk is.
    • Een 7/16 fractie kan worden afgerond tot 8/16 (of 1/2). 7/16 kan nog steeds ongeveer als de helft worden gezien, maar je moet onthouden dat de vereenvoudigde versie iets meer is dan het echte aantal. Een wiskundige manier om dit uit te drukken is: (1/2 - 1/16).

Methode twee van twee:
Fracties visueel inschatten

  1. 1 Bepaal de geldigheid van een visuele schatting. Een fractie visueel communiceren maakt het duidelijk voor andere mensen. Ze zijn een perfecte manier om verhoudingen met anderen uit te drukken, vooral als die mensen geen wiskundige achtergrond hebben. Visuele schattingen zijn het meest geschikt om de ene fractie te vergelijken met de andere. Het menselijk oog is getraind om dingen te vergelijken en te meten, zelfs zonder wiskundige ervaring. Door iets in visuele termen te plaatsen, wordt de geest verlicht door puur abstract, op cijfers gebaseerd denken. Visuele schattingen zijn ook perfect voor gebruik in casual, "real life" -instellingen.[7]
    • Een 12/16-breuklijn kan er bijvoorbeeld in een puur numerieke vorm groter uitzien dan 7/8, maar een eenvoudige grafiek van de twee naast elkaar zal gemakkelijk laten zien dat de laatste groter is dan de eerste.
    • De twee belangrijkste soorten visueel geïllustreerde breuken zijn lijn- en cirkelgrafieken.[8] Lijnen zijn het beste voor metingen, terwijl cirkels (of "cirkeldiagrammen") het best zijn voor het weergeven van verhoudingen.
  2. 2 Kies een visueel model.[9] Verschillende visuele modellen passen op verschillende mensen. Of u nu een cirkeldiagram, rechthoek, diagram of een andere manier wilt gebruiken om uw verhoudingen te visualiseren, een illustratie van een breuk geeft u een referentiepunt om er in meer concrete termen over na te denken.
    • Verschillende verhoudingen kunnen worden aangegeven door verschillende tinten of kleuren. Twee gearceerde tertsen van een cirkeldiagram geven bijvoorbeeld een 2/3 breuk aan.
    • Het is een goed idee om met een paar visuele modellen te spelen die dezelfde reeks breuken gebruiken. Dit laat u zien hoe verschillende modellen hetzelfde kunnen vertegenwoordigen.
  3. 3 Illustreer fracties met fysieke stukken. Met chocoladestukjes, bouwstenen of zelfs steentjes kun je je breuken schatten door verschillende stukjes in groepen te zetten. Een fractie met 50 delen (17/50 + 33/50) kan worden uitgedrukt door 50 stukjes in twee groepen te scheiden. Hiermee kunt u visueel zien hoe de ene fractie groter is dan de andere.
    • Door twee of meer verhoudingen naast elkaar te illustreren, kunt u eenvoudig zien welke fracties het grootst zijn en welke het kleinst zijn. Het menselijk oog zal het onderscheid bijna zonder na te denken kunnen identificeren, dus het is een mooie manier om het onderscheid in duidelijke bewoordingen te communiceren.[10]
  4. 4 Stapel je verhoudingen naast elkaar.[11] Relatieve breuken zijn overal om ons heen en we maken vaak keuzes op basis van het schatten van breuken zonder er zelfs maar aan te denken. Als je op zoek bent naar een manier om je breukschatting te oefenen, plaats dan twee items met verschillende hoogten naast elkaar. Probeer van daaruit te raden welk deel van de grootte van het grotere object overeenkomt met het kleinere.
    • U kunt uw antwoorden controleren door een liniaal te plaatsen en vervolgens de juiste afmetingen van uw items te meten.
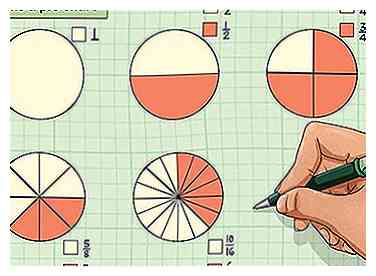  5. 5 Maak een cirkeldiagram. Cirkeldiagrammen zijn een geweldige manier om verhoudingen op een visuele manier uit te drukken. Als je een visueel denker bent, is het een goed idee om je afgeronde breuken in een cirkel te werken. Van daaruit kunt u uw schatting uiten zonder te moeten vertrouwen op afgeronde cijfers die mogelijk niet juist zijn. In tegenstelling tot grafieken (die meestal op exacte gegevens vertrouwen) moet een cirkeldiagram een ​​snelle manier zijn om visuele gegevens weer te geven. Het is over het algemeen eenvoudiger om de delen van een cirkel visueel te analyseren dan andere visuele modellen, omdat een volledige cirkel een geheel vertegenwoordigt.