Hoewel het eenvoudig is hele getallen als 1, 3 en 8 op grootte te bestellen, kunnen breuken in één oogopslag moeilijk te meten zijn. Als elk lager getal, of de noemer, hetzelfde is, kunt u ze als hele getallen rangschikken, bijvoorbeeld 1/5, 3/5 en 8/5. Anders kunt u uw lijst met breuken wijzigen om dezelfde noemer te gebruiken, zonder de grootte van een breuk te wijzigen. Dit wordt gemakkelijker met oefenen, en je kunt een paar "trucjes" leren als je slechts twee breuken vergelijkt, of als je topzware "ongepaste" breuken sorteert zoals 7/3.
Methode één van de drie:
Elk gewenst aantal breuken bestellen
-
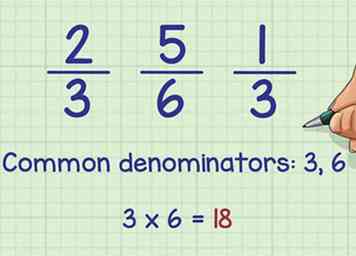 1 Zoek een gemeenschappelijke noemer voor alle breuken. Gebruik een van deze methoden om een noemer of lager getal van een breuk te vinden die u kunt gebruiken om elke breuk in de lijst te herschrijven, zodat u ze gemakkelijk kunt vergelijken. Dit wordt a genoemd gemene deler, of de kleinste gemene deler als het de laagst mogelijke is:[1]
1 Zoek een gemeenschappelijke noemer voor alle breuken. Gebruik een van deze methoden om een noemer of lager getal van een breuk te vinden die u kunt gebruiken om elke breuk in de lijst te herschrijven, zodat u ze gemakkelijk kunt vergelijken. Dit wordt a genoemd gemene deler, of de kleinste gemene deler als het de laagst mogelijke is:[1] - Vermenigvuldig elke verschillende deler samen. Als u bijvoorbeeld 2/3, 5/6 en 1/3 vergelijkt, vermenigvuldigt u de twee verschillende noemers: 3 x 6 = 18. Dit is een eenvoudige methode, maar zal vaak resulteren in een veel groter aantal dan de andere methoden, die moeilijk kunnen zijn om mee te werken.
- Of lijst de veelvouden van elke noemer in een afzonderlijke kolom, tot u een aantal opmerkt dat in elke kolom verschijnt. Gebruik dit nummer. Vergelijk bijvoorbeeld 2/3, 5/6 en 1/3 met een paar veelvouden van 3: 3, 6, 9, 12, 15, 18. Geef vervolgens de veelvouden van 6: 6, 12, 18 op. 18 verschijnt op beide lijsten, gebruik dat nummer. (Je zou ook 12 kunnen gebruiken, maar onderstaande voorbeelden gaan ervan uit dat je 18 gebruikt)
-
 2 Converteer elke breuk zodat deze de gemeenschappelijke noemer gebruikt. Onthoud dat als u de boven- en onderkant van een breuk met hetzelfde aantal vermenigvuldigt, de breuk nog steeds dezelfde grootte heeft. Gebruik deze techniek op elke breuk, één voor één, zodat elke de gemeenschappelijke noemer als het onderste getal gebruikt. Probeer het voor 2/3, 5/6 en 1/3, met behulp van de gemeenschappelijke noemer 18:
2 Converteer elke breuk zodat deze de gemeenschappelijke noemer gebruikt. Onthoud dat als u de boven- en onderkant van een breuk met hetzelfde aantal vermenigvuldigt, de breuk nog steeds dezelfde grootte heeft. Gebruik deze techniek op elke breuk, één voor één, zodat elke de gemeenschappelijke noemer als het onderste getal gebruikt. Probeer het voor 2/3, 5/6 en 1/3, met behulp van de gemeenschappelijke noemer 18: - 18 ÷ 3 = 6, dus 2/3 = (2x6) / (3x6) = 12/18
- 18 ÷ 6 = 3, dus 5/6 = (5x3) / (6x3) = 15/18
- 18 ÷ 3 = 6, dus 1/3 = (1x6) / (3x6) = 6/18
-
 3 Gebruik het bovenste cijfer om de breuken te bestellen. Nu ze allemaal dezelfde noemer hebben, zijn de breuken gemakkelijk te vergelijken. Gebruik hun topnummer, of teller, om ze te rangschikken van minst naar grootst. Rangschikking van de breuken die we hierboven vonden, krijgen we: 18/6, 12/18, 15/18.
3 Gebruik het bovenste cijfer om de breuken te bestellen. Nu ze allemaal dezelfde noemer hebben, zijn de breuken gemakkelijk te vergelijken. Gebruik hun topnummer, of teller, om ze te rangschikken van minst naar grootst. Rangschikking van de breuken die we hierboven vonden, krijgen we: 18/6, 12/18, 15/18. -
 4 Zet elke breuk terug in zijn oorspronkelijke vorm. Houd de breuken in dezelfde volgorde, maar keer ze terug naar de oorspronkelijke vorm. U kunt dit doen door te onthouden hoe elke fractie is getransformeerd, of door de boven- en onderkant van elke fractie opnieuw te splitsen:
4 Zet elke breuk terug in zijn oorspronkelijke vorm. Houd de breuken in dezelfde volgorde, maar keer ze terug naar de oorspronkelijke vorm. U kunt dit doen door te onthouden hoe elke fractie is getransformeerd, of door de boven- en onderkant van elke fractie opnieuw te splitsen: - 6/18 = (6 ÷ 6)/(18 ÷ 6) = 1/3
- 12/18 = (12 ÷ 6)/(18 ÷ 6) = 2/3
- 15/18 = (15 ÷ 3)/(18 ÷ 3) = 5/6
- Het antwoord is "1/3, 2/3, 5/6"
Methode twee van drie:
Bestellen van twee breuken met behulp van cross-vermenigvuldiging
-
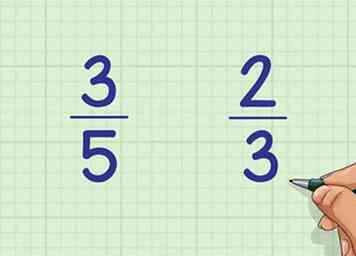 1 Schrijf de twee breuken naast elkaar. Vergelijk bijvoorbeeld de breuk 3/5 en de breuk 2/3. Schrijf deze naast elkaar op de pagina: 3/5 aan de linkerkant en 2/3 aan de rechterkant.
1 Schrijf de twee breuken naast elkaar. Vergelijk bijvoorbeeld de breuk 3/5 en de breuk 2/3. Schrijf deze naast elkaar op de pagina: 3/5 aan de linkerkant en 2/3 aan de rechterkant. -
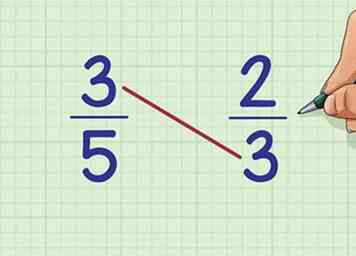 2 Vermenigvuldig de bovenkant van de eerste breuk met de onderkant van de tweede breuk. In ons voorbeeld het bovenste getal, of teller, van de eerste fractie (3/5) is 3. Het onderste nummer, of noemer, van de tweede fractie (2/3) is ook 3. Vermenigvuldig deze samen: 3 x 3 =?
2 Vermenigvuldig de bovenkant van de eerste breuk met de onderkant van de tweede breuk. In ons voorbeeld het bovenste getal, of teller, van de eerste fractie (3/5) is 3. Het onderste nummer, of noemer, van de tweede fractie (2/3) is ook 3. Vermenigvuldig deze samen: 3 x 3 =? - Deze methode wordt genoemd kruislings vermenigvuldigen, omdat u getallen op een diagonale lijn tegenover elkaar vermenigvuldigt.
-
 3 Schrijf je antwoord naast de eerste breuk. Schrijf het product of antwoord op uw vermenigvuldigingsprobleem, naast de eerste breuk op de pagina. In ons voorbeeld 3 x 3 = 9, dus je zou schrijven 9 naast de eerste breuk, aan de linkerkant van de pagina.
3 Schrijf je antwoord naast de eerste breuk. Schrijf het product of antwoord op uw vermenigvuldigingsprobleem, naast de eerste breuk op de pagina. In ons voorbeeld 3 x 3 = 9, dus je zou schrijven 9 naast de eerste breuk, aan de linkerkant van de pagina. -
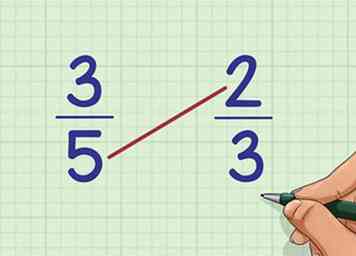 4 Vermenigvuldig de top van de tweede breuk met de onderkant van de eerste. Om uit te vinden welke fractie groter is, moeten we ons antwoord hierboven vergelijken met het antwoord op een ander vermenigvuldigingsprobleem. Vermenigvuldig deze twee getallen samen. Voor ons voorbeeld (vergelijken van 3/5 en 2/3), vermenigvuldig 2 x 5 samen.
4 Vermenigvuldig de top van de tweede breuk met de onderkant van de eerste. Om uit te vinden welke fractie groter is, moeten we ons antwoord hierboven vergelijken met het antwoord op een ander vermenigvuldigingsprobleem. Vermenigvuldig deze twee getallen samen. Voor ons voorbeeld (vergelijken van 3/5 en 2/3), vermenigvuldig 2 x 5 samen. -
 5 Schrijf dit antwoord naast de tweede breuk. Schrijf het antwoord op dit tweede vermenigvuldigingsprobleem naast de tweede breuk. In dit voorbeeld is het antwoord 10.
5 Schrijf dit antwoord naast de tweede breuk. Schrijf het antwoord op dit tweede vermenigvuldigingsprobleem naast de tweede breuk. In dit voorbeeld is het antwoord 10. -
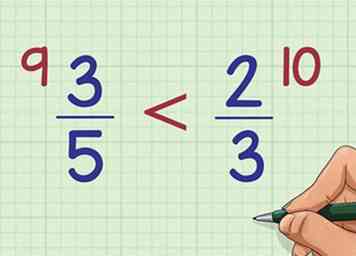 6 Vergelijk de waarden van de twee cross-producten. De antwoorden op de vermenigvuldigingsproblemen in deze methode worden genoemd cross-producten. Als een crossproduct groter is dan het andere, is de fractie naast dat crossproduct ook groter dan de andere fractie. In ons voorbeeld, omdat 9 kleiner is dan 10, betekent dit dat 3/5 minder dan 2/3 moet zijn.
6 Vergelijk de waarden van de twee cross-producten. De antwoorden op de vermenigvuldigingsproblemen in deze methode worden genoemd cross-producten. Als een crossproduct groter is dan het andere, is de fractie naast dat crossproduct ook groter dan de andere fractie. In ons voorbeeld, omdat 9 kleiner is dan 10, betekent dit dat 3/5 minder dan 2/3 moet zijn. - Onthoud, schrijf altijd het crossproduct naast de breuk waarvan top nummer dat je hebt gebruikt.
-
 7 Begrijp waarom dit werkt. Als u twee breuken wilt vergelijken, converteert u ze meestal om ze dezelfde noemer of een lager deel van de breuk te geven. In het geheim is dit wat cross-vermenigvuldiging doet![2] Het springt gewoon over het feitelijk schrijven van de noemers, want zodra de twee breuken dezelfde hebben, hoeft u alleen de bovenste twee getallen te vergelijken. Hier is onszelfde voorbeeld (3/5 vs 2/3), geschreven zonder de cross-multiplying "shortcut":
7 Begrijp waarom dit werkt. Als u twee breuken wilt vergelijken, converteert u ze meestal om ze dezelfde noemer of een lager deel van de breuk te geven. In het geheim is dit wat cross-vermenigvuldiging doet![2] Het springt gewoon over het feitelijk schrijven van de noemers, want zodra de twee breuken dezelfde hebben, hoeft u alleen de bovenste twee getallen te vergelijken. Hier is onszelfde voorbeeld (3/5 vs 2/3), geschreven zonder de cross-multiplying "shortcut": - 05/03 = (3x3) / (5x3) = 9/15
- 03/02 = (2x5) / (3x5) = 10/15
- 9/15 is minder dan 10/15
- Daarom is 3/5 minder dan 2/3
Methode drie van drie:
Fracties groter dan één bestellen
-
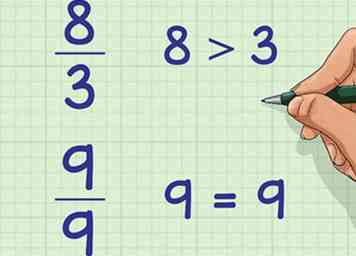 1 Gebruik dit voor breuken met een topnummer gelijk aan of groter dan het onderste getal. Als een breuk een topnummer heeft, of teller, dat is groter dan het onderste getal, of noemer, het is groter dan één.8/3 is een voorbeeld van dit type breuk. Je kunt dit ook gebruiken voor breuken met een gelijke teller en noemer, zoals 9/9. Beide fracties zijn voorbeelden van onjuiste breuken.[3]
1 Gebruik dit voor breuken met een topnummer gelijk aan of groter dan het onderste getal. Als een breuk een topnummer heeft, of teller, dat is groter dan het onderste getal, of noemer, het is groter dan één.8/3 is een voorbeeld van dit type breuk. Je kunt dit ook gebruiken voor breuken met een gelijke teller en noemer, zoals 9/9. Beide fracties zijn voorbeelden van onjuiste breuken.[3] - U kunt nog steeds de andere methoden voor deze breuken gebruiken. Deze methode helpt deze breuken echter logisch en kan sneller zijn.
-
 2 Converteer elke ongepaste fractie naar een gemengd getal. Verander ze in een mix van hele getallen en breuken. Soms kun je dit misschien in je hoofd doen. Bijvoorbeeld 9/9 = 1. Gebruik in andere divisies lange divisies om uit te vinden hoe vaak de teller telt gelijkmatig in de noemer. De rest in dat langeafstandsprobleem, indien aanwezig, wordt "overgebleven" als een breuk. Bijvoorbeeld:
2 Converteer elke ongepaste fractie naar een gemengd getal. Verander ze in een mix van hele getallen en breuken. Soms kun je dit misschien in je hoofd doen. Bijvoorbeeld 9/9 = 1. Gebruik in andere divisies lange divisies om uit te vinden hoe vaak de teller telt gelijkmatig in de noemer. De rest in dat langeafstandsprobleem, indien aanwezig, wordt "overgebleven" als een breuk. Bijvoorbeeld: - 8/3 = 2 + 2/3
- 9/9 = 1
- 19/4 = 4 + 3/4
- 13/6 = 2 + 1/6
-
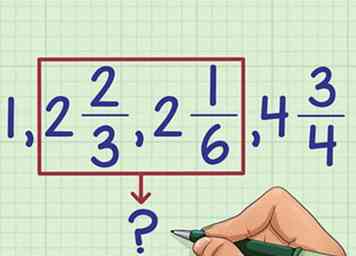 3 Sorteer de gemengde getallen op geheel getal. Nu er geen ongepaste breuken zijn, heb je een beter idee van hoe groot elk nummer is. Negeer de breuken nu en sorteer de breuken in groepen op hele getal:
3 Sorteer de gemengde getallen op geheel getal. Nu er geen ongepaste breuken zijn, heb je een beter idee van hoe groot elk nummer is. Negeer de breuken nu en sorteer de breuken in groepen op hele getal: - 1 is het kleinst
- 2 + 2/3 en 2 + 1/6 (we weten nog niet welke groter is dan de andere)
- 4 + 3/4 is de grootste
-
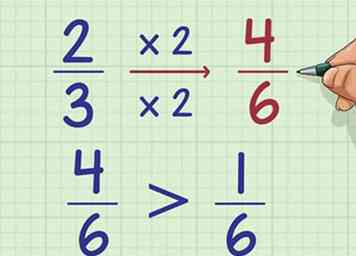 4 Vergelijk zo nodig de breuken in elke groep. Als je meerdere gemengde getallen hebt met hetzelfde hele getal, zoals 2 + 2/3 en 2 + 1/6, vergelijk dan het breukdeel van het getal om te zien welke groter is. U kunt elk van de methoden in de andere secties gebruiken om dit te doen. Hier is een voorbeeld dat 2 + 2/3 en 2 + 1/6 vergelijkt, waarbij de breuken in dezelfde noemer worden omgezet:
4 Vergelijk zo nodig de breuken in elke groep. Als je meerdere gemengde getallen hebt met hetzelfde hele getal, zoals 2 + 2/3 en 2 + 1/6, vergelijk dan het breukdeel van het getal om te zien welke groter is. U kunt elk van de methoden in de andere secties gebruiken om dit te doen. Hier is een voorbeeld dat 2 + 2/3 en 2 + 1/6 vergelijkt, waarbij de breuken in dezelfde noemer worden omgezet: - 2/3 = (2x2) / (3x2) = 4/6
- 1/6 = 1/6
- 4/6 is groter dan 1/6
- 2 + 4/6 is groter dan 2 + 1/6
- 2 + 2/3 is groter dan 2 + 1/6
-
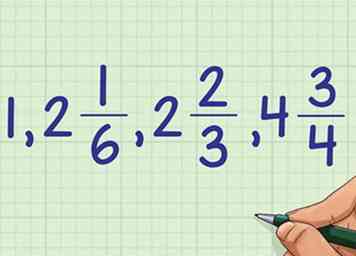 5 Gebruik uw resultaten om uw hele lijst met gemengde nummers te sorteren. Nadat u de breuken in elke groep gemengde getallen hebt gesorteerd, kunt u uw volledige lijst sorteren: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.
5 Gebruik uw resultaten om uw hele lijst met gemengde nummers te sorteren. Nadat u de breuken in elke groep gemengde getallen hebt gesorteerd, kunt u uw volledige lijst sorteren: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4. -
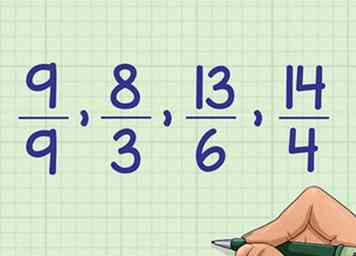 6 Zet de gemengde nummers terug naar hun oorspronkelijke breuken. Houd de volgorde hetzelfde, maar maak de aangebrachte wijzigingen ongedaan en schrijf de nummers op als de originele onjuiste breuken: 9/9, 8/3, 13/6, 19/4.
6 Zet de gemengde nummers terug naar hun oorspronkelijke breuken. Houd de volgorde hetzelfde, maar maak de aangebrachte wijzigingen ongedaan en schrijf de nummers op als de originele onjuiste breuken: 9/9, 8/3, 13/6, 19/4.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
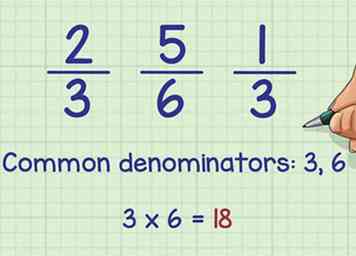 1 Zoek een gemeenschappelijke noemer voor alle breuken. Gebruik een van deze methoden om een noemer of lager getal van een breuk te vinden die u kunt gebruiken om elke breuk in de lijst te herschrijven, zodat u ze gemakkelijk kunt vergelijken. Dit wordt a genoemd gemene deler, of de kleinste gemene deler als het de laagst mogelijke is:[1]
1 Zoek een gemeenschappelijke noemer voor alle breuken. Gebruik een van deze methoden om een noemer of lager getal van een breuk te vinden die u kunt gebruiken om elke breuk in de lijst te herschrijven, zodat u ze gemakkelijk kunt vergelijken. Dit wordt a genoemd gemene deler, of de kleinste gemene deler als het de laagst mogelijke is:[1]  2 Converteer elke breuk zodat deze de gemeenschappelijke noemer gebruikt. Onthoud dat als u de boven- en onderkant van een breuk met hetzelfde aantal vermenigvuldigt, de breuk nog steeds dezelfde grootte heeft. Gebruik deze techniek op elke breuk, één voor één, zodat elke de gemeenschappelijke noemer als het onderste getal gebruikt. Probeer het voor 2/3, 5/6 en 1/3, met behulp van de gemeenschappelijke noemer 18:
2 Converteer elke breuk zodat deze de gemeenschappelijke noemer gebruikt. Onthoud dat als u de boven- en onderkant van een breuk met hetzelfde aantal vermenigvuldigt, de breuk nog steeds dezelfde grootte heeft. Gebruik deze techniek op elke breuk, één voor één, zodat elke de gemeenschappelijke noemer als het onderste getal gebruikt. Probeer het voor 2/3, 5/6 en 1/3, met behulp van de gemeenschappelijke noemer 18:  3 Gebruik het bovenste cijfer om de breuken te bestellen. Nu ze allemaal dezelfde noemer hebben, zijn de breuken gemakkelijk te vergelijken. Gebruik hun topnummer, of teller, om ze te rangschikken van minst naar grootst. Rangschikking van de breuken die we hierboven vonden, krijgen we: 18/6, 12/18, 15/18.
3 Gebruik het bovenste cijfer om de breuken te bestellen. Nu ze allemaal dezelfde noemer hebben, zijn de breuken gemakkelijk te vergelijken. Gebruik hun topnummer, of teller, om ze te rangschikken van minst naar grootst. Rangschikking van de breuken die we hierboven vonden, krijgen we: 18/6, 12/18, 15/18.  4 Zet elke breuk terug in zijn oorspronkelijke vorm. Houd de breuken in dezelfde volgorde, maar keer ze terug naar de oorspronkelijke vorm. U kunt dit doen door te onthouden hoe elke fractie is getransformeerd, of door de boven- en onderkant van elke fractie opnieuw te splitsen:
4 Zet elke breuk terug in zijn oorspronkelijke vorm. Houd de breuken in dezelfde volgorde, maar keer ze terug naar de oorspronkelijke vorm. U kunt dit doen door te onthouden hoe elke fractie is getransformeerd, of door de boven- en onderkant van elke fractie opnieuw te splitsen: 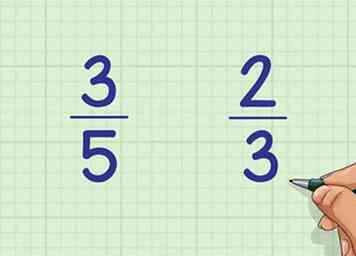 1 Schrijf de twee breuken naast elkaar. Vergelijk bijvoorbeeld de breuk 3/5 en de breuk 2/3. Schrijf deze naast elkaar op de pagina: 3/5 aan de linkerkant en 2/3 aan de rechterkant.
1 Schrijf de twee breuken naast elkaar. Vergelijk bijvoorbeeld de breuk 3/5 en de breuk 2/3. Schrijf deze naast elkaar op de pagina: 3/5 aan de linkerkant en 2/3 aan de rechterkant. 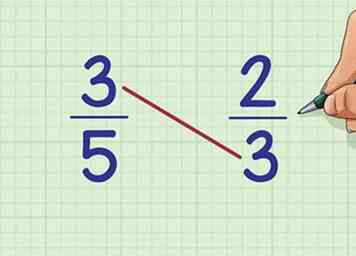 2 Vermenigvuldig de bovenkant van de eerste breuk met de onderkant van de tweede breuk. In ons voorbeeld het bovenste getal, of teller, van de eerste fractie (3/5) is 3. Het onderste nummer, of noemer, van de tweede fractie (2/3) is ook 3. Vermenigvuldig deze samen: 3 x 3 =?
2 Vermenigvuldig de bovenkant van de eerste breuk met de onderkant van de tweede breuk. In ons voorbeeld het bovenste getal, of teller, van de eerste fractie (3/5) is 3. Het onderste nummer, of noemer, van de tweede fractie (2/3) is ook 3. Vermenigvuldig deze samen: 3 x 3 =?  3 Schrijf je antwoord naast de eerste breuk. Schrijf het product of antwoord op uw vermenigvuldigingsprobleem, naast de eerste breuk op de pagina. In ons voorbeeld 3 x 3 = 9, dus je zou schrijven 9 naast de eerste breuk, aan de linkerkant van de pagina.
3 Schrijf je antwoord naast de eerste breuk. Schrijf het product of antwoord op uw vermenigvuldigingsprobleem, naast de eerste breuk op de pagina. In ons voorbeeld 3 x 3 = 9, dus je zou schrijven 9 naast de eerste breuk, aan de linkerkant van de pagina.  4 Vermenigvuldig de top van de tweede breuk met de onderkant van de eerste. Om uit te vinden welke fractie groter is, moeten we ons antwoord hierboven vergelijken met het antwoord op een ander vermenigvuldigingsprobleem. Vermenigvuldig deze twee getallen samen. Voor ons voorbeeld (vergelijken van 3/5 en 2/3), vermenigvuldig 2 x 5 samen.
4 Vermenigvuldig de top van de tweede breuk met de onderkant van de eerste. Om uit te vinden welke fractie groter is, moeten we ons antwoord hierboven vergelijken met het antwoord op een ander vermenigvuldigingsprobleem. Vermenigvuldig deze twee getallen samen. Voor ons voorbeeld (vergelijken van 3/5 en 2/3), vermenigvuldig 2 x 5 samen.  5 Schrijf dit antwoord naast de tweede breuk. Schrijf het antwoord op dit tweede vermenigvuldigingsprobleem naast de tweede breuk. In dit voorbeeld is het antwoord 10.
5 Schrijf dit antwoord naast de tweede breuk. Schrijf het antwoord op dit tweede vermenigvuldigingsprobleem naast de tweede breuk. In dit voorbeeld is het antwoord 10. 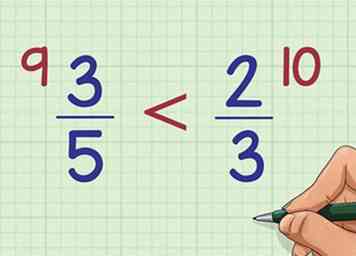 6 Vergelijk de waarden van de twee cross-producten. De antwoorden op de vermenigvuldigingsproblemen in deze methode worden genoemd cross-producten. Als een crossproduct groter is dan het andere, is de fractie naast dat crossproduct ook groter dan de andere fractie. In ons voorbeeld, omdat 9 kleiner is dan 10, betekent dit dat 3/5 minder dan 2/3 moet zijn.
6 Vergelijk de waarden van de twee cross-producten. De antwoorden op de vermenigvuldigingsproblemen in deze methode worden genoemd cross-producten. Als een crossproduct groter is dan het andere, is de fractie naast dat crossproduct ook groter dan de andere fractie. In ons voorbeeld, omdat 9 kleiner is dan 10, betekent dit dat 3/5 minder dan 2/3 moet zijn.  7 Begrijp waarom dit werkt. Als u twee breuken wilt vergelijken, converteert u ze meestal om ze dezelfde noemer of een lager deel van de breuk te geven. In het geheim is dit wat cross-vermenigvuldiging doet![2] Het springt gewoon over het feitelijk schrijven van de noemers, want zodra de twee breuken dezelfde hebben, hoeft u alleen de bovenste twee getallen te vergelijken. Hier is onszelfde voorbeeld (3/5 vs 2/3), geschreven zonder de cross-multiplying "shortcut":
7 Begrijp waarom dit werkt. Als u twee breuken wilt vergelijken, converteert u ze meestal om ze dezelfde noemer of een lager deel van de breuk te geven. In het geheim is dit wat cross-vermenigvuldiging doet![2] Het springt gewoon over het feitelijk schrijven van de noemers, want zodra de twee breuken dezelfde hebben, hoeft u alleen de bovenste twee getallen te vergelijken. Hier is onszelfde voorbeeld (3/5 vs 2/3), geschreven zonder de cross-multiplying "shortcut": 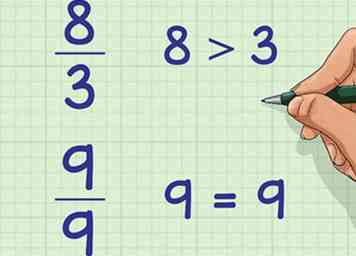 1 Gebruik dit voor breuken met een topnummer gelijk aan of groter dan het onderste getal. Als een breuk een topnummer heeft, of teller, dat is groter dan het onderste getal, of noemer, het is groter dan één.8/3 is een voorbeeld van dit type breuk. Je kunt dit ook gebruiken voor breuken met een gelijke teller en noemer, zoals 9/9. Beide fracties zijn voorbeelden van onjuiste breuken.[3]
1 Gebruik dit voor breuken met een topnummer gelijk aan of groter dan het onderste getal. Als een breuk een topnummer heeft, of teller, dat is groter dan het onderste getal, of noemer, het is groter dan één.8/3 is een voorbeeld van dit type breuk. Je kunt dit ook gebruiken voor breuken met een gelijke teller en noemer, zoals 9/9. Beide fracties zijn voorbeelden van onjuiste breuken.[3]  2 Converteer elke ongepaste fractie naar een gemengd getal. Verander ze in een mix van hele getallen en breuken. Soms kun je dit misschien in je hoofd doen. Bijvoorbeeld 9/9 = 1. Gebruik in andere divisies lange divisies om uit te vinden hoe vaak de teller telt gelijkmatig in de noemer. De rest in dat langeafstandsprobleem, indien aanwezig, wordt "overgebleven" als een breuk. Bijvoorbeeld:
2 Converteer elke ongepaste fractie naar een gemengd getal. Verander ze in een mix van hele getallen en breuken. Soms kun je dit misschien in je hoofd doen. Bijvoorbeeld 9/9 = 1. Gebruik in andere divisies lange divisies om uit te vinden hoe vaak de teller telt gelijkmatig in de noemer. De rest in dat langeafstandsprobleem, indien aanwezig, wordt "overgebleven" als een breuk. Bijvoorbeeld: 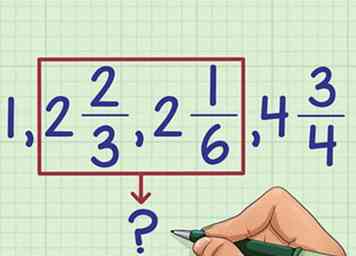 3 Sorteer de gemengde getallen op geheel getal. Nu er geen ongepaste breuken zijn, heb je een beter idee van hoe groot elk nummer is. Negeer de breuken nu en sorteer de breuken in groepen op hele getal:
3 Sorteer de gemengde getallen op geheel getal. Nu er geen ongepaste breuken zijn, heb je een beter idee van hoe groot elk nummer is. Negeer de breuken nu en sorteer de breuken in groepen op hele getal: 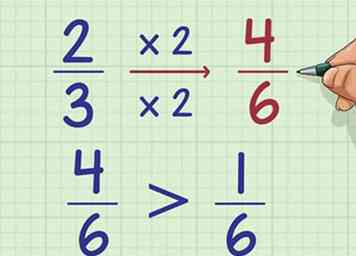 4 Vergelijk zo nodig de breuken in elke groep. Als je meerdere gemengde getallen hebt met hetzelfde hele getal, zoals 2 + 2/3 en 2 + 1/6, vergelijk dan het breukdeel van het getal om te zien welke groter is. U kunt elk van de methoden in de andere secties gebruiken om dit te doen. Hier is een voorbeeld dat 2 + 2/3 en 2 + 1/6 vergelijkt, waarbij de breuken in dezelfde noemer worden omgezet:
4 Vergelijk zo nodig de breuken in elke groep. Als je meerdere gemengde getallen hebt met hetzelfde hele getal, zoals 2 + 2/3 en 2 + 1/6, vergelijk dan het breukdeel van het getal om te zien welke groter is. U kunt elk van de methoden in de andere secties gebruiken om dit te doen. Hier is een voorbeeld dat 2 + 2/3 en 2 + 1/6 vergelijkt, waarbij de breuken in dezelfde noemer worden omgezet: 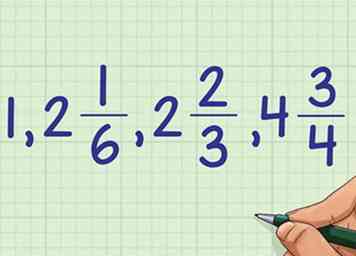 5 Gebruik uw resultaten om uw hele lijst met gemengde nummers te sorteren. Nadat u de breuken in elke groep gemengde getallen hebt gesorteerd, kunt u uw volledige lijst sorteren: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.
5 Gebruik uw resultaten om uw hele lijst met gemengde nummers te sorteren. Nadat u de breuken in elke groep gemengde getallen hebt gesorteerd, kunt u uw volledige lijst sorteren: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4. 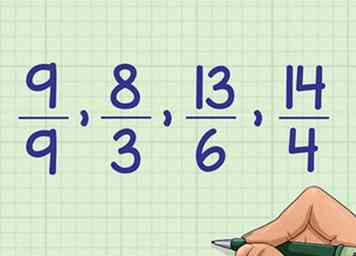 6 Zet de gemengde nummers terug naar hun oorspronkelijke breuken. Houd de volgorde hetzelfde, maar maak de aangebrachte wijzigingen ongedaan en schrijf de nummers op als de originele onjuiste breuken: 9/9, 8/3, 13/6, 19/4.
6 Zet de gemengde nummers terug naar hun oorspronkelijke breuken. Houd de volgorde hetzelfde, maar maak de aangebrachte wijzigingen ongedaan en schrijf de nummers op als de originele onjuiste breuken: 9/9, 8/3, 13/6, 19/4.