Hoe Pi voor jezelf te ontdekken met behulp van cirkels

Hoe werd de wiskundige constante genaamd "pi" ontdekt - en had je het kunnen ontdekken? Wel, ja, met een beetje nauwgezet werk, kunt u het slimme idee en de bron van het concept ontdekken, evenals zijn niet-meer abstracte betekenis krijgen en een geschatte waarde vinden. Het is ingepakt in elke cirkel en bol - maar waar en hoe kon je het in de aard van cirkels hebben voorzien? Blijf lezen voor gedetailleerde instructies voor uw sprong naar ontdekkingen in wiskunde.

Methode één van de vier:
Basisgeometrie van de cirkel in een vlak

1. 1 Begin je inzicht in de geometrie van de cirkel in een vlak op te frissen. Je weet veel over het punt, het vlak en de ruimte, en ze zijn niet eens gedefinieerd in de studie van de geometrie, maar ze worden beschreven zoals ze worden gebruikt.
   • Wat is een cirkel? De volgende informatie moet deel uitmaken van uw (basis) begrip van dingen over kringen, maar u kunt veel meer leren terwijl u doorgaat.
   • op gelijke afstand - is een afkorting voor "van gelijke afstand"
   • cirkel - alle punten op gelijke afstand, vanuit het midden (middelpunt).
   • De volgende feiten hebben betrekking op, maar zijn niet deel van de cirkel:
     • centrum - het punt op gelijke afstand van elk punt in de cirkel,
     • radius - het segment (geeft de lengte aan) tussen één eindpunt in het midden en het andere uiteinde op de cirkel (het is die "gelijke afstand" genoemd),
     • diameter - het segment (geeft de lengte aan) door het midden en tussen de twee eindpunten op de cirkel,
     • segment, gebied, sector, en opgenomen of ingeschreven vormen binnen, maar niet onderdeel van, de cirkel, en
     • omtrek - de afstand één keer rond de cirkel.
       • Ja, dat woord is lang en vreemd; dus, denk aan "de afstand rondom cirkelvormige fence."

Methode twee van vier:
Maak eerst een formule

1. 1 Ontdek je omtrekformule: De diameter kan ongeveer drie keer worden gebogen en met de uiteinden rond de cirkel worden geplaatst, wat betekent dat: drie diameters plus een kleine fractie van diameter = Circumference. Laten we dat C = 3 X d noemen, ongeveer. Klaar (dat was te gemakkelijk ...), net zoals je oorspronkelijk had moeten doen terwijl je de omtrek ongeveer 3000 of 4000 jaar geleden ontdekte; nu maak je dat idee schoon ... In de oudheid was wiskunde als een mystieke studie en je "ontdekking" was een onderdeel van de uitdrukking van wiskundige mysteries.
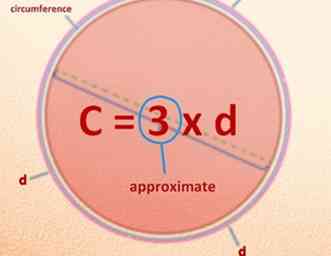2. 2 Absorbeer dat ruwe, intuïtieve idee van pi, ongeveer 3, en besef dat het gemakkelijk kan worden aangetoond dat het niet precies drie is. Nu zult u het nauwkeuriger maken.

Methode drie van vier:
Ontdek pi nauwkeuriger

1. 1 Nummer vier verschillende maten van ronde containers of deksels. Een bol of bol (bol) kan ook werken, maar het is moeilijker om te meten.
2. 2 Ontvang een niet-rekbare, niet-kinky string en een meterstok, maatstaf of liniaal.
3. 3 Maak een grafiek (of tabel) zoals de volgende: Omtrek | diameter | quotiënt C / d =?
   1. __________|________|__________________
   2. __________|________|__________________
   3. __________|________|__________________
   4. __________|________|__________________
4. 4 Meet nauwkeurig rond elk van de vier ronde items door er een touwtje omheen te wikkelen. Markeer de afstand een keer eromheen op de string. Dit is de omtrek: het is net als de omtrek, maar de omtrek van een cirkel- de afstand rond een cirkel - heet de omtrek, niet omtrek, meestal.
5. 5 Strek het deel van de draad dat u hebt gemarkeerd als de afstand rond de cirkel recht en meet het. Noteer uw meting van de omtrek met decimalen. Speld of plak de uiteinden van de snaar om deze nauwkeurig te meten (recht en uitgebreid tot de volledige maat), omdat je de snaar rond het ronde voorwerp moest spannen, dus nu zou je hem in de lengte vaster aantrekken.
6. 6 Draai de container ondersteboven zodat u het midden onderaan kunt vinden en markeren, zodat u de diameter kunt meten met decimalen (ook wel decimale breuken genoemd).
7. 7 Meet over elke cirkel precies door het midden van elk van de vier items met een rechte randmaat (meterstok, maatstaf of liniaal). Dit is de diameter.
   • Opmerking: vermenigvuldig twee keer de straal, dat wil zeggen: "2 X radius = diameter" wordt ook geschreven als "2r = d".
8. 8 Verdeel elke omtrek door de diameter van dezelfde cirkel. De vier deling problemen van C / d = _____, zouden ongeveer 3 of 3.1 (of ongeveer 3.14 moeten zijn als uw metingen nauwkeurig zijn); dus wat is pi: het is een nummer. Het is een verhouding. Het heeft betrekking op diameter tot omtrek. Natuurlijk kan het helpen met nauwkeurige metingen met behulp van verdelers, die vergelijkbaar zijn met een kompas.
9. 9 Gemiddelde van de vier antwoorden op het delingprobleem door deze vier quotiënten toe te voegen en te delen door 4, en dat zou een nauwkeuriger resultaat moeten geven (bijvoorbeeld als uw vier divisies u gaven: 3,1 + 3,15 + 3,1 + 3,2 = ____ / 4 = ____? Dat is 12.55 / 4 = 3.1375, en kan worden afgerond naar 3.14).
   Dat is het idee van "pi". Het aantal diameters dat de omtrek maakt (de hele tijd, zo is het constante) ... Dat is de constante "pi". Dat aantal diameters.
   • Ook past de radius iets meer dan 6 (2 keer pi) maal rond een cirkel, evenals het feit dat hij weet dat de diameter drie keer gaat; dus dat impliceert een omtrekformule C = 2 X 3.14 X r, dat is gewoon = 3.14 X d ... door gebruik te maken van 2r is d ("Heb het", knik ja. "Ja!" Maar lees het en denk erover na tot het dringt echt door, als het nog niet kristalhelder is).
10. 10 Neem ten slotte de middellijnstring en gebruik deze om de lengte driemaal af te snijden van de omtrekstring. Doe dit voor elk van de containers. Het overgebleven stuk touw van elk van de snarenuitsnijding van de omtrek zal ongeveer dezelfde lengte hebben.De meetlengte van dit korte stuk touw moet .1415 zijn, wat slechts een voorbeeld is van het krijgen van ongeveer 3.14 ...

Methode vier van vier:
Hint van de leraar

1. 1 Help studenten om echt van deze oefening te genieten. Dit kan een geweldig draai-moment zijn, een van die momenten waarop ze zich voelen: "Ik snap het! Wow!", "Ik hou meer van wiskunde dan ooit / meer dan ik dacht". Behandel dit als een wetenschappelijk experiment, als een soort "wiskundig / wetenschappelijk" vakoverschrijdende opdracht.
2. 2 Verzin een mysterieus opdrachtenblad voor een les of een buitenproject, als je een leraar of een tutor bent.
3. 3 Tip een beetje. "Toon ze, of laat ze je tonen, maar doe het niet vertel het hen! Laat ze dingen ontdekken. "Als het een weggeefactie is, is de uitkomst te gemakkelijk voor wat het allemaal laat zien. Zorg er dus voor dat studenten het als een mysterie kunnen ontdekken en een" Eureka! ervaring… ", niet gewoon horen of lezen over een experiment.
   • Je zou niet zo meteen door een lezing of lezingpresentatie willen gaan als hier, maar wees subtiel in de eerste lijn, faciliteer en verduidelijk het nadat je studenten hebt gevraagd om hun grafieken te presenteren als posters van wat ze hebben ontdekt, op hun manier! Studenten kunnen hun presentaties op een wiskundemuur plaatsen en trots zijn op hun scherpzinnigheid, slimheid, erdoorheen werken!
4. 4 Gebruik dit als een geweldige in-class project (cross teaching) "kunst-wiskunde-kunst" -opdracht - of voor uw studenten om mee naar huis te nemen als een project voor extra credit buiten de wiskundeles. En nadat je deze hebt toegepast, zou je het leuk kunnen vinden om te leren leiden tot een geweldige leraar.