Exponenten zijn een manier om nummers te identificeren die door zichzelf worden vermenigvuldigd. Ze worden vaak genoemd bevoegdheden. In de algebra kom je vaak exponenten tegen, dus het is handig om te weten hoe je met dit soort expressies werkt. U kunt exponentiële expressies vermenigvuldigen net zoals u andere getallen kunt vermenigvuldigen. Als de exponenten dezelfde basis hebben, kunt u een snelkoppeling gebruiken om te vereenvoudigen en te berekenen; anders is het vermenigvuldigen van exponentiële uitdrukkingen nog steeds een eenvoudige bewerking.
Methode één van de drie:
Exponenten vermenigvuldigen met dezelfde basis
-
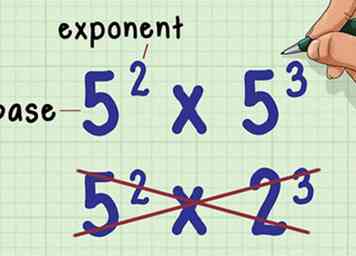 1 Zorg ervoor dat de exponenten dezelfde basis hebben. De basis is het grote getal in de exponentiële uitdrukking. U kunt deze methode alleen gebruiken als de uitdrukkingen die u vermenigvuldigt dezelfde basis hebben.
1 Zorg ervoor dat de exponenten dezelfde basis hebben. De basis is het grote getal in de exponentiële uitdrukking. U kunt deze methode alleen gebruiken als de uitdrukkingen die u vermenigvuldigt dezelfde basis hebben. - U kunt deze methode bijvoorbeeld gebruiken om te vermenigvuldigen , omdat ze allebei dezelfde basis hebben (5). Aan de andere kant kun je deze methode niet gebruiken om te vermenigvuldigen , omdat ze verschillende bases hebben (5 en 2).
-
 2 Voeg de exponenten samen toe. Herschrijf de expressie, behoud dezelfde basis maar zet de som van de oorspronkelijke exponenten als de nieuwe exponent.[1]
2 Voeg de exponenten samen toe. Herschrijf de expressie, behoud dezelfde basis maar zet de som van de oorspronkelijke exponenten als de nieuwe exponent.[1] - Bijvoorbeeld, als u vermenigvuldigt , je zou de basis van 5 behouden en de exponenten samenvoegen:
- Bijvoorbeeld, als u vermenigvuldigt , je zou de basis van 5 behouden en de exponenten samenvoegen:
-
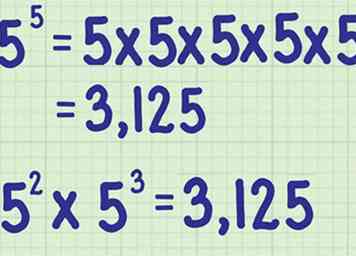 3 Bereken de uitdrukking. Een exponent vertelt je hoe vaak je een getal alleen vermenigvuldigt.[2] U kunt een rekenmachine gebruiken om eenvoudig een exponentiële uitdrukking te berekenen, maar u kunt ook met de hand berekenen.
3 Bereken de uitdrukking. Een exponent vertelt je hoe vaak je een getal alleen vermenigvuldigt.[2] U kunt een rekenmachine gebruiken om eenvoudig een exponentiële uitdrukking te berekenen, maar u kunt ook met de hand berekenen. - Bijvoorbeeld
Zo,
- Bijvoorbeeld
Methode twee van drie:
Exponenten vermenigvuldigen met verschillende basen
-
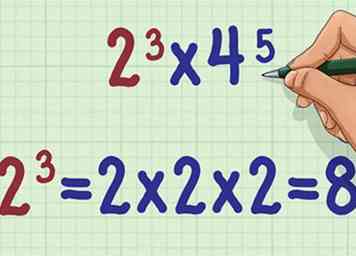 1 Bereken de eerste exponentiële uitdrukking. Omdat de exponenten verschillende bases hebben, is er geen snelkoppeling om ze te vermenigvuldigen. Bereken de exponent met een rekenmachine of met de hand. Onthoud dat een exponent je vertelt hoe vaak je een getal alleen vermenigvuldigt.
1 Bereken de eerste exponentiële uitdrukking. Omdat de exponenten verschillende bases hebben, is er geen snelkoppeling om ze te vermenigvuldigen. Bereken de exponent met een rekenmachine of met de hand. Onthoud dat een exponent je vertelt hoe vaak je een getal alleen vermenigvuldigt. - Bijvoorbeeld, als u vermenigvuldigt , je moet opmerken dat ze niet dezelfde basis hebben. Dus je zal eerst berekenen .
-
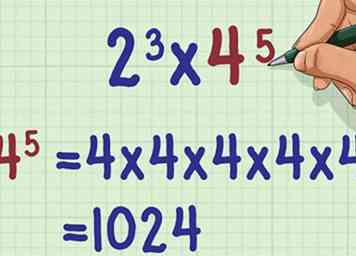 2 Bereken de tweede exponentiële uitdrukking. Doe dit door het basisnummer zelf te vermenigvuldigen, hoe vaak de exponent ook zegt.
2 Bereken de tweede exponentiële uitdrukking. Doe dit door het basisnummer zelf te vermenigvuldigen, hoe vaak de exponent ook zegt. - Bijvoorbeeld,
-
 3 Herschrijf het probleem met behulp van de nieuwe berekeningen. Volgens hetzelfde voorbeeld wordt uw nieuwe probleem .
3 Herschrijf het probleem met behulp van de nieuwe berekeningen. Volgens hetzelfde voorbeeld wordt uw nieuwe probleem . -
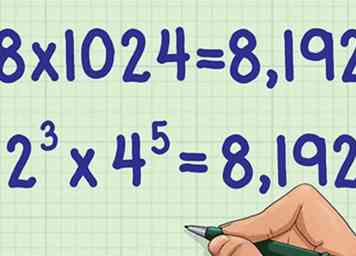 4 Vermenigvuldig de twee cijfers. Dit geeft je het laatste antwoord op het probleem.
4 Vermenigvuldig de twee cijfers. Dit geeft je het laatste antwoord op het probleem. - Bijvoorbeeld: Zo, .
Methode drie van drie:
Gemengde variabelen vermenigvuldigen met exponenten
-
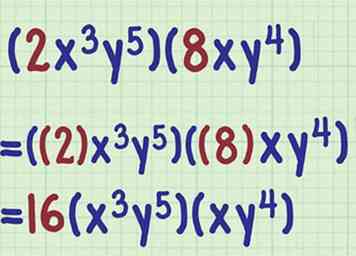 1 Vermenigvuldig de coëfficiënten. Vermenigvuldig deze zoals je zou doen met hele getallen. Verplaats het nummer naar de buitenkant van de haakjes.[3]
1 Vermenigvuldig de coëfficiënten. Vermenigvuldig deze zoals je zou doen met hele getallen. Verplaats het nummer naar de buitenkant van de haakjes.[3] - Bijvoorbeeld, vermenigvuldigen , zou je eerst berekenen .
-
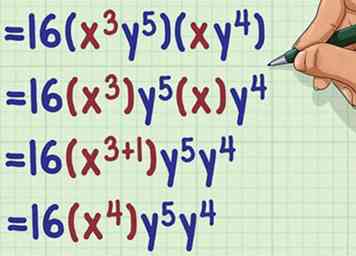 2 Voeg de exponenten van de eerste variabele toe. Zorg ervoor dat u alleen de exponenten van termen toevoegt met dezelfde basis (variabele). Vergeet niet dat als een variabele geen exponent laat zien, dit een exponent van 1 is.[4]
2 Voeg de exponenten van de eerste variabele toe. Zorg ervoor dat u alleen de exponenten van termen toevoegt met dezelfde basis (variabele). Vergeet niet dat als een variabele geen exponent laat zien, dit een exponent van 1 is.[4] - Bijvoorbeeld:
- Bijvoorbeeld:
-
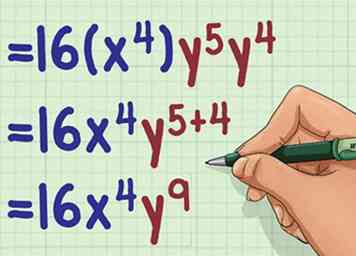 3 Voeg de exponenten van de overige variabelen toe. Zorg ervoor om exponenten toe te voegen met dezelfde basis, en vergeet niet dat variabelen zonder exponenten een begrepen exponent hebben van 1.
3 Voeg de exponenten van de overige variabelen toe. Zorg ervoor om exponenten toe te voegen met dezelfde basis, en vergeet niet dat variabelen zonder exponenten een begrepen exponent hebben van 1. - Bijvoorbeeld:
- Bijvoorbeeld:
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
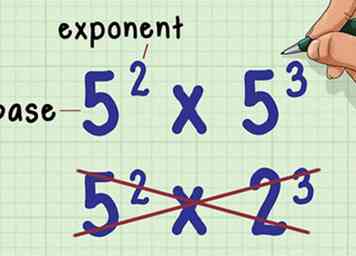 1 Zorg ervoor dat de exponenten dezelfde basis hebben. De basis is het grote getal in de exponentiële uitdrukking. U kunt deze methode alleen gebruiken als de uitdrukkingen die u vermenigvuldigt dezelfde basis hebben.
1 Zorg ervoor dat de exponenten dezelfde basis hebben. De basis is het grote getal in de exponentiële uitdrukking. U kunt deze methode alleen gebruiken als de uitdrukkingen die u vermenigvuldigt dezelfde basis hebben.  2 Voeg de exponenten samen toe. Herschrijf de expressie, behoud dezelfde basis maar zet de som van de oorspronkelijke exponenten als de nieuwe exponent.[1]
2 Voeg de exponenten samen toe. Herschrijf de expressie, behoud dezelfde basis maar zet de som van de oorspronkelijke exponenten als de nieuwe exponent.[1] 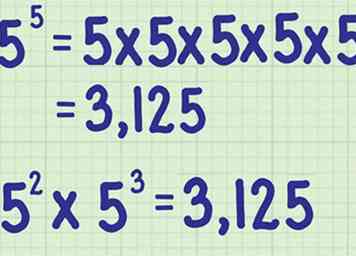 3 Bereken de uitdrukking. Een exponent vertelt je hoe vaak je een getal alleen vermenigvuldigt.[2] U kunt een rekenmachine gebruiken om eenvoudig een exponentiële uitdrukking te berekenen, maar u kunt ook met de hand berekenen.
3 Bereken de uitdrukking. Een exponent vertelt je hoe vaak je een getal alleen vermenigvuldigt.[2] U kunt een rekenmachine gebruiken om eenvoudig een exponentiële uitdrukking te berekenen, maar u kunt ook met de hand berekenen. 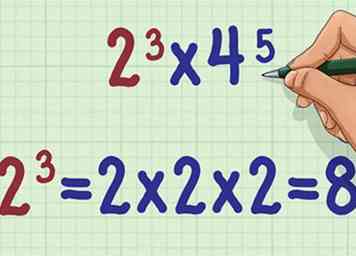 1 Bereken de eerste exponentiële uitdrukking. Omdat de exponenten verschillende bases hebben, is er geen snelkoppeling om ze te vermenigvuldigen. Bereken de exponent met een rekenmachine of met de hand. Onthoud dat een exponent je vertelt hoe vaak je een getal alleen vermenigvuldigt.
1 Bereken de eerste exponentiële uitdrukking. Omdat de exponenten verschillende bases hebben, is er geen snelkoppeling om ze te vermenigvuldigen. Bereken de exponent met een rekenmachine of met de hand. Onthoud dat een exponent je vertelt hoe vaak je een getal alleen vermenigvuldigt. 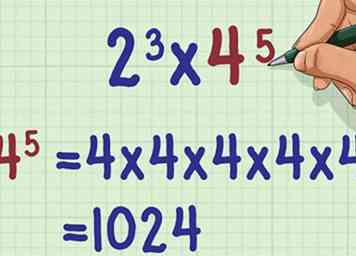 2 Bereken de tweede exponentiële uitdrukking. Doe dit door het basisnummer zelf te vermenigvuldigen, hoe vaak de exponent ook zegt.
2 Bereken de tweede exponentiële uitdrukking. Doe dit door het basisnummer zelf te vermenigvuldigen, hoe vaak de exponent ook zegt.  3 Herschrijf het probleem met behulp van de nieuwe berekeningen. Volgens hetzelfde voorbeeld wordt uw nieuwe probleem
3 Herschrijf het probleem met behulp van de nieuwe berekeningen. Volgens hetzelfde voorbeeld wordt uw nieuwe probleem 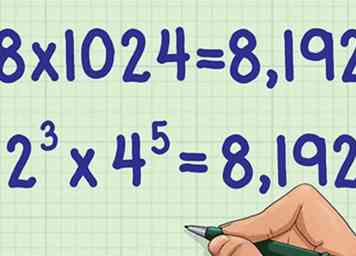 4 Vermenigvuldig de twee cijfers. Dit geeft je het laatste antwoord op het probleem.
4 Vermenigvuldig de twee cijfers. Dit geeft je het laatste antwoord op het probleem. 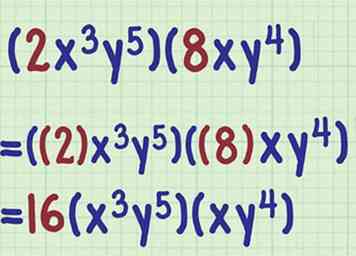 1 Vermenigvuldig de coëfficiënten. Vermenigvuldig deze zoals je zou doen met hele getallen. Verplaats het nummer naar de buitenkant van de haakjes.[3]
1 Vermenigvuldig de coëfficiënten. Vermenigvuldig deze zoals je zou doen met hele getallen. Verplaats het nummer naar de buitenkant van de haakjes.[3] 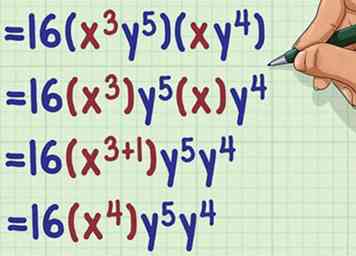 2 Voeg de exponenten van de eerste variabele toe. Zorg ervoor dat u alleen de exponenten van termen toevoegt met dezelfde basis (variabele). Vergeet niet dat als een variabele geen exponent laat zien, dit een exponent van 1 is.[4]
2 Voeg de exponenten van de eerste variabele toe. Zorg ervoor dat u alleen de exponenten van termen toevoegt met dezelfde basis (variabele). Vergeet niet dat als een variabele geen exponent laat zien, dit een exponent van 1 is.[4] 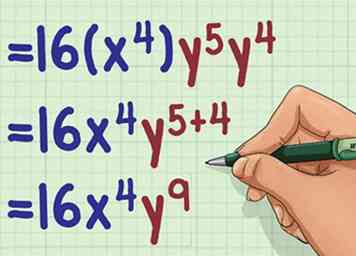 3 Voeg de exponenten van de overige variabelen toe. Zorg ervoor om exponenten toe te voegen met dezelfde basis, en vergeet niet dat variabelen zonder exponenten een begrepen exponent hebben van 1.
3 Voeg de exponenten van de overige variabelen toe. Zorg ervoor om exponenten toe te voegen met dezelfde basis, en vergeet niet dat variabelen zonder exponenten een begrepen exponent hebben van 1.