Grafieken van punten in het coördinaatvlak

Als u punten op het coördinatenvlak wilt tekenen, moet u de organisatie van het coördinatenvlak begrijpen en weten wat u met die (x, y) coördinaten moet doen. Als u wilt weten hoe u punten op het coördinatenvlak kunt tekenen, volgt u gewoon deze stappen.

Deel een van de drie:
Het coördinatenvlak begrijpen

1. 1 Begrijp de assen van het coördinaatvlak. Wanneer u een punt op het coördinatenvlak in een grafiek weergeeft, kunt u het in (x, y) vorm tekenen. Dit is wat u moet weten:
   • De x-as gaat naar links en rechts, de tweede coördinaat bevindt zich op de y-as.
   • De y-as gaat op en neer.
   • Positieve cijfers gaan omhoog of naar rechts (afhankelijk van de as). Negatieve getallen gaan naar links of naar beneden.
2. 2 Begrijp de kwadranten op het coördinatenvlak. Vergeet niet dat een grafiek vier kwadranten heeft (meestal aangeduid in Romeinse cijfers). Je moet weten in welk kwadrant het vliegtuig zich bevindt.
   • Kwadrant krijg ik (+, +); kwadrant I bevindt zich boven en links van de y-as.
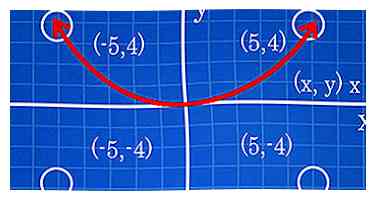
   • Kwadrant IV krijgt (+, -); kwadrant IV bevindt zich onder de x-as en rechts van de y-as. (5,4) staat in kwadrant I.
   • (-5,4) bevindt zich in kwadrant II. (-5, -4) bevindt zich in kwadrant III. (5, -4) bevindt zich in Quadrant IV.

Tweede deel van de drie:
Een enkel punt tekenen

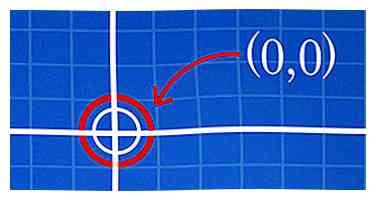1. 1 Begin bij (0, 0) of de oorsprong. Ga gewoon naar (0, 0), dat is de kruising van de x- en y-assen, precies in het midden van het coördinatenvlak.^[1]
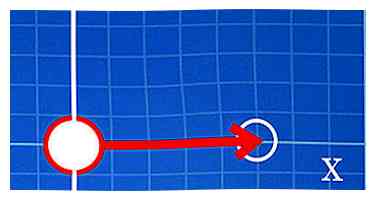2. 2 Beweeg x-eenheden naar rechts of links. Laten we zeggen dat je met de set coördinaten werkt (5, -4). Uw x-coördinaat is 5. Aangezien vijf positief is, moet u vijf eenheden naar rechts verplaatsen. Als het negatief was, zou je meer dan 5 eenheden naar links verplaatsen.
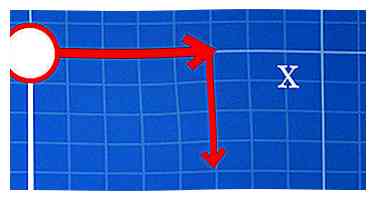3. 3 Beweeg over y-eenheden omhoog of omlaag. Begin waar je was gebleven, 5 eenheden rechts van (0, 0). Omdat je y-coördinaat -4 is, moet je vier eenheden naar beneden verplaatsen. Als het 4 was, zou je vier eenheden omhoog gaan.
4. 4 Markeer het punt. Markeer het gevonden punt door 5 eenheden naar rechts en 4 eenheden naar beneden te verplaatsen, het punt (5, -4), dat zich in het 4e kwadrant bevindt. Je bent helemaal klaar.

Derde deel van de drie:
Geavanceerde technieken volgen

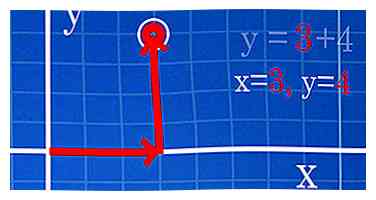1. 1 Leer hoe u punten kunt uitrekenen als u met een vergelijking werkt. Als u een formule zonder coördinaten heeft, moet u uw punten vinden door een willekeurige coördinaat voor x te kiezen en te zien wat de formule voor y spuwt. Blijf gewoon doorgaan totdat je genoeg punten hebt gevonden en ze allemaal in een grafiek kunt zetten, en ze eventueel kunt verbinden. Hier leest u hoe u het kunt doen, of u nu met een eenvoudige lijn werkt, of een ingewikkeldere vergelijking zoals een parabool:
   • Grafiekpunten van een lijn. Laten we zeggen dat de vergelijking y = x + 4 is. Kies dus een willekeurig getal voor x, zoals 3, en kijk wat je krijgt voor y. y = 3 + 4 = 7, dus je hebt het punt gevonden (3, 7).
   • Grafiekpunten van een kwadratische vergelijking. Laten we zeggen dat de vergelijking van de parabool is y = x² + 2. Doe hetzelfde: kies een willekeurig getal voor x en kijk wat je krijgt voor y. Het kiezen van 0 voor x is het gemakkelijkst. y = 0² + 2, dus y = 2. U hebt het punt gevonden (0, 2).
2. 2 Verbind de punten indien nodig. Als je een lijngrafiek moet maken, een cirkel moet tekenen, of alle punten van een parabool of een andere kwadratische vergelijking moet verbinden, dan moet je de punten verbinden. Als je een lineaire vergelijking hebt, teken dan lijnen die de punten verbinden van links naar rechts. Als u met een kwadratische vergelijking werkt, verbindt u de punten met gebogen lijnen.
   • Tenzij u alleen een punt in een grafiek opneemt, hebt u ten minste twee punten nodig. Een lijn vereist twee punten.
   • Een cirkel heeft twee punten nodig als er een centraal punt is; drie als het centrum niet is opgenomen (gebruik drie) (tenzij je instructeur het midden van de cirkel in het probleem heeft opgenomen).
   • Een parabool vereist drie punten, één is het absolute minimum of maximum; de andere twee punten moeten tegenpolen zijn.
   • Een hyperbool vereist zes punten; drie op elke as.
3. 3 Begrijp hoe het wijzigen van de vergelijking de grafiek verandert. Dit zijn de verschillende manieren waarop het wijzigen van de vergelijking de grafiek verandert:
   • Door de x-coördinaat te wijzigen, wordt de vergelijking naar links of rechts verplaatst.
   • Door een constante toe te voegen, wordt de vergelijking hoger of lager.
   • Negatief draaien (vermenigvuldigen met -1) klapt het om; als het een lijn is, verandert deze van omhoog of omlaag of omhoog.
   • Als u het met een ander getal vermenigvuldigt, wordt de helling verhoogd of verlaagd.
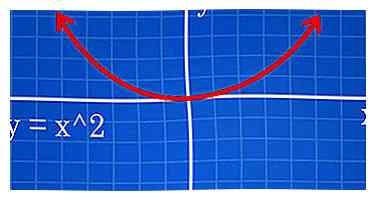4. 4 Volg een voorbeeld om te zien hoe het wijzigen van de vergelijking de grafiek verandert. Beschouw de vergelijking y = x ^ 2; een parabool met zijn basis op (0,0). Hier zijn de verschillen die u ziet als u de vergelijking aanpast:
   • y = (x-2) ^ 2 is dezelfde parabool, behalve dat het twee velden rechts van de oorsprong is uitgezet; de basis is nu op (2,0).
   • y = x ^ 2 + 2 is nog steeds dezelfde parabool, behalve dat het nu twee spaties hoger is op (0,2).
   • y = -x ^ 2 (het negatief wordt toegepast nadat de exponent ^ 2) ondersteboven is y = x ^ 2; de basis is (0,0).
   • y = 5x ^ 2 is nog steeds een parabool, maar wordt nog sneller groter, waardoor het er dunner uitziet.