Een rationele functie is een vergelijking die de vorm aanneemt Y = N (X) / D (X) waarbij N en D polynomen zijn. Pogingen om met de hand een nauwkeurige grafiek van één te schetsen, kunnen een uitgebreide beoordeling zijn van veel van de belangrijkste wiskundeonderwerpen op de middelbare school, van elementaire algebra tot differentiële calculus. Bekijk het volgende voorbeeld: Y = (2X2 - 6X + 5)/(4X + 2).
Stappen
-
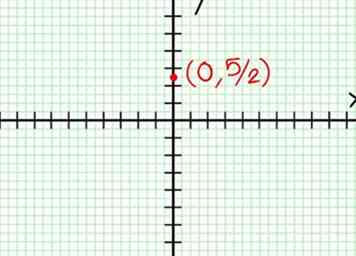 1 Vind de Y onderscheppen. Eenvoudig ingesteld X = 0. Alles behalve de constante voorwaarden verdwijnen en verdwijnen Y = 5/2. Dit uitdrukken als een coördinatenpaar, (0, 5/2) is een punt in de grafiek. Grafiek dat punt.
1 Vind de Y onderscheppen. Eenvoudig ingesteld X = 0. Alles behalve de constante voorwaarden verdwijnen en verdwijnen Y = 5/2. Dit uitdrukken als een coördinatenpaar, (0, 5/2) is een punt in de grafiek. Grafiek dat punt. -
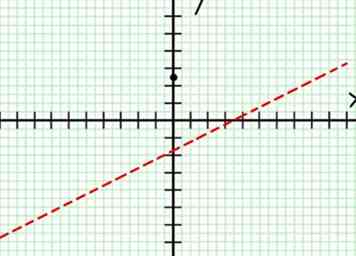 2 Zoek de horizontale asymptoot. Verdeel de noemer lang in de teller om het gedrag van te bepalen Y voor grote absolute waarden van X. In dit voorbeeld toont de verdeling dat Y = (1/2)X - (7/4) + 17/(8X + 4). Voor grote positieve of negatieve waarden van x, 17 / (8X + 4) nadert nul en de grafiek benadert de lijn Y = (1/2)X - (7/4). Gebruik deze lijn om een stippellijn of een lichtlijn te tekenen.
2 Zoek de horizontale asymptoot. Verdeel de noemer lang in de teller om het gedrag van te bepalen Y voor grote absolute waarden van X. In dit voorbeeld toont de verdeling dat Y = (1/2)X - (7/4) + 17/(8X + 4). Voor grote positieve of negatieve waarden van x, 17 / (8X + 4) nadert nul en de grafiek benadert de lijn Y = (1/2)X - (7/4). Gebruik deze lijn om een stippellijn of een lichtlijn te tekenen. - Als de mate van de teller kleiner is dan de mate van de noemer, is er geen verdeling om te doen en is de asymptoot Y = 0.
- Als deg (N) = deg (D), is de asymptoot een horizontale lijn in de verhouding van de leidende coëfficiënten.
- Als deg (N) = deg (D) + 1, is de asymptoot een lijn waarvan de helling de verhouding is van de leidende coëfficiënten.
- Als deg (N)> deg (D) + 1, dan voor grote waarden van |X|, Y gaat snel naar positieve of negatieve oneindigheid als een kwadratische, kubische of hogere graad. In dit geval is het waarschijnlijk niet de moeite waard om het quotiënt van de deling nauwkeurig in kaart te brengen.
-
 3 Zoek de nullen. Een rationale functie heeft een nul als de teller nul is, dus stel N in (X) = 0. In het voorbeeld 2X2 - 6X + 5 = 0. De discriminant van deze kwadratische is b2 - 4ac = 62 - 4 * 2 * 5 = 36 - 40 = -4. Omdat de discriminant negatief is, N (X), en bijgevolg f (X), heeft geen echte wortels. De grafiek overschrijdt nooit de X-as. Als er nullen zijn gevonden, voegt u die punten toe aan de grafiek.
3 Zoek de nullen. Een rationale functie heeft een nul als de teller nul is, dus stel N in (X) = 0. In het voorbeeld 2X2 - 6X + 5 = 0. De discriminant van deze kwadratische is b2 - 4ac = 62 - 4 * 2 * 5 = 36 - 40 = -4. Omdat de discriminant negatief is, N (X), en bijgevolg f (X), heeft geen echte wortels. De grafiek overschrijdt nooit de X-as. Als er nullen zijn gevonden, voegt u die punten toe aan de grafiek. -
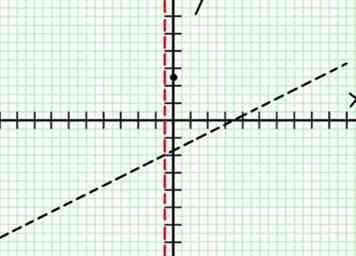 4 Zoek de verticale asymptoten. Een verticale asymptoot vindt plaats wanneer de noemer nul is. Instelling 4X + 2 = 0 geeft de verticale lijn X = -1/2. Geef elke verticale asymptoot een grafiek met een lichte of gestreepte lijn. Als een waarde van X maakt beide N (X) = 0 en D (X) = 0, er kan al dan niet een verticale asymptoot zijn. Dit is zeldzaam, maar zie de tips voor hoe ermee om te gaan als dit voorkomt.
4 Zoek de verticale asymptoten. Een verticale asymptoot vindt plaats wanneer de noemer nul is. Instelling 4X + 2 = 0 geeft de verticale lijn X = -1/2. Geef elke verticale asymptoot een grafiek met een lichte of gestreepte lijn. Als een waarde van X maakt beide N (X) = 0 en D (X) = 0, er kan al dan niet een verticale asymptoot zijn. Dit is zeldzaam, maar zie de tips voor hoe ermee om te gaan als dit voorkomt. -
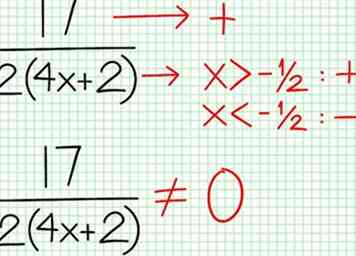 5 Kijk naar de rest van de divisie in stap 2. Wanneer is het positief, negatief of nul? In het voorbeeld is de teller van de rest 17, wat altijd positief is. De noemer, 4X + 2, is positief aan de rechterkant van de verticale asymptoot en negatief aan de linkerkant. Dit betekent dat de grafiek de lineaire asymptoot uit het bovenstaande benadert voor grote positieve waarden van X en van onderaf voor grote negatieve waarden van X. Sinds 17 / (8X + 4) kan nooit nul zijn, deze grafiek snijdt nooit de lijn Y = (1/2)X - (7/4). Voeg nu niets toe aan de grafiek, maar noteer deze conclusies voor later.
5 Kijk naar de rest van de divisie in stap 2. Wanneer is het positief, negatief of nul? In het voorbeeld is de teller van de rest 17, wat altijd positief is. De noemer, 4X + 2, is positief aan de rechterkant van de verticale asymptoot en negatief aan de linkerkant. Dit betekent dat de grafiek de lineaire asymptoot uit het bovenstaande benadert voor grote positieve waarden van X en van onderaf voor grote negatieve waarden van X. Sinds 17 / (8X + 4) kan nooit nul zijn, deze grafiek snijdt nooit de lijn Y = (1/2)X - (7/4). Voeg nu niets toe aan de grafiek, maar noteer deze conclusies voor later. -
 6 Zoek de lokale extrema. Een lokaal extremum kan optreden wanneer N '(X) D (X) - N (X) D '(X) = 0. In het voorbeeld, N '(X) = 4X - 6 en D '(X) = 4. N '(X) D (X) - N (X) D '(X) = (4X - 6)(4X + 2) - (2X2 - 6X + 5) * 4 = 0. Uitbreiden, termen combineren en delen door 4 bladeren X2 + X - 4 = 0. De kwadratische formule toont wortels in de buurt X = 3/2 en X = -5/2. (Deze verschillen ongeveer 0,06 van de exacte waarden, maar onze grafiek zal niet precies genoeg zijn om zich zorgen te maken over dat detailniveau. Het kiezen van een fatsoenlijke rationele benadering maakt de volgende stap eenvoudiger.)
6 Zoek de lokale extrema. Een lokaal extremum kan optreden wanneer N '(X) D (X) - N (X) D '(X) = 0. In het voorbeeld, N '(X) = 4X - 6 en D '(X) = 4. N '(X) D (X) - N (X) D '(X) = (4X - 6)(4X + 2) - (2X2 - 6X + 5) * 4 = 0. Uitbreiden, termen combineren en delen door 4 bladeren X2 + X - 4 = 0. De kwadratische formule toont wortels in de buurt X = 3/2 en X = -5/2. (Deze verschillen ongeveer 0,06 van de exacte waarden, maar onze grafiek zal niet precies genoeg zijn om zich zorgen te maken over dat detailniveau. Het kiezen van een fatsoenlijke rationele benadering maakt de volgende stap eenvoudiger.) -
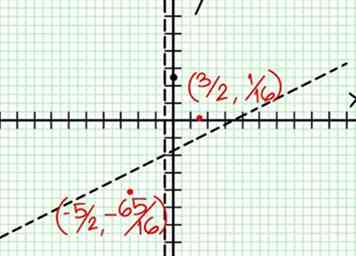 7 Vind de Y-waarden van elk lokaal extremum. Sluit de X-waarden van de vorige stap terug naar de oorspronkelijke rationale functie om het overeenkomstige te vinden Y-waarden. In het voorbeeld, f (3/2) = 1/16 en f (-5/2) = -65/16. Voeg deze punten (3/2, 1/16) en (-5/2, -65/16) toe aan de grafiek. Aangezien we in de vorige stap benaderd zijn, zijn dit niet de exacte minima en maxima, maar zijn ze waarschijnlijk dichtbij. (We weten (3/2, 1/16) ligt heel dicht bij het lokale minimum, vanaf stap 3 weten we dat Y is altijd positief wanneer X > -1/2 en we vonden een waarde zo klein als 1/16, dus althans in dit geval is de fout waarschijnlijk kleiner dan de dikte van de lijn.)
7 Vind de Y-waarden van elk lokaal extremum. Sluit de X-waarden van de vorige stap terug naar de oorspronkelijke rationale functie om het overeenkomstige te vinden Y-waarden. In het voorbeeld, f (3/2) = 1/16 en f (-5/2) = -65/16. Voeg deze punten (3/2, 1/16) en (-5/2, -65/16) toe aan de grafiek. Aangezien we in de vorige stap benaderd zijn, zijn dit niet de exacte minima en maxima, maar zijn ze waarschijnlijk dichtbij. (We weten (3/2, 1/16) ligt heel dicht bij het lokale minimum, vanaf stap 3 weten we dat Y is altijd positief wanneer X > -1/2 en we vonden een waarde zo klein als 1/16, dus althans in dit geval is de fout waarschijnlijk kleiner dan de dikte van de lijn.) -
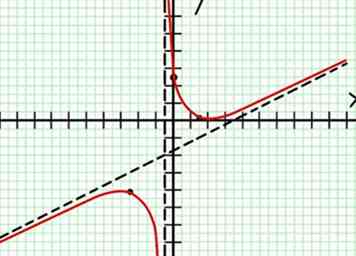 8 Verbind de punten en schuif de grafiek soepel uit van de bekende punten naar de asymptoten en zorg ervoor ze vanuit de juiste richting te benaderen. Zorg ervoor dat u de X-as behalve op de punten die je al bij stap 3 hebt gevonden. Steek de horizontale of lineaire asymptoot niet over, behalve bij de punten die je al in stap 5 hebt gevonden. Verander niet van opwaarts hellend naar schuin aflopend, behalve bij het uiterste in de vorige stap .
8 Verbind de punten en schuif de grafiek soepel uit van de bekende punten naar de asymptoten en zorg ervoor ze vanuit de juiste richting te benaderen. Zorg ervoor dat u de X-as behalve op de punten die je al bij stap 3 hebt gevonden. Steek de horizontale of lineaire asymptoot niet over, behalve bij de punten die je al in stap 5 hebt gevonden. Verander niet van opwaarts hellend naar schuin aflopend, behalve bij het uiterste in de vorige stap .
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Vind de Y onderscheppen. Eenvoudig ingesteld X = 0. Alles behalve de constante voorwaarden verdwijnen en verdwijnen Y = 5/2. Dit uitdrukken als een coördinatenpaar, (0, 5/2) is een punt in de grafiek. Grafiek dat punt.
1 Vind de Y onderscheppen. Eenvoudig ingesteld X = 0. Alles behalve de constante voorwaarden verdwijnen en verdwijnen Y = 5/2. Dit uitdrukken als een coördinatenpaar, (0, 5/2) is een punt in de grafiek. Grafiek dat punt.  2 Zoek de horizontale asymptoot. Verdeel de noemer lang in de teller om het gedrag van te bepalen Y voor grote absolute waarden van X. In dit voorbeeld toont de verdeling dat Y = (1/2)X - (7/4) + 17/(8X + 4). Voor grote positieve of negatieve waarden van x, 17 / (8X + 4) nadert nul en de grafiek benadert de lijn Y = (1/2)X - (7/4). Gebruik deze lijn om een stippellijn of een lichtlijn te tekenen.
2 Zoek de horizontale asymptoot. Verdeel de noemer lang in de teller om het gedrag van te bepalen Y voor grote absolute waarden van X. In dit voorbeeld toont de verdeling dat Y = (1/2)X - (7/4) + 17/(8X + 4). Voor grote positieve of negatieve waarden van x, 17 / (8X + 4) nadert nul en de grafiek benadert de lijn Y = (1/2)X - (7/4). Gebruik deze lijn om een stippellijn of een lichtlijn te tekenen.  3 Zoek de nullen. Een rationale functie heeft een nul als de teller nul is, dus stel N in (X) = 0. In het voorbeeld 2X2 - 6X + 5 = 0. De discriminant van deze kwadratische is b2 - 4ac = 62 - 4 * 2 * 5 = 36 - 40 = -4. Omdat de discriminant negatief is, N (X), en bijgevolg f (X), heeft geen echte wortels. De grafiek overschrijdt nooit de X-as. Als er nullen zijn gevonden, voegt u die punten toe aan de grafiek.
3 Zoek de nullen. Een rationale functie heeft een nul als de teller nul is, dus stel N in (X) = 0. In het voorbeeld 2X2 - 6X + 5 = 0. De discriminant van deze kwadratische is b2 - 4ac = 62 - 4 * 2 * 5 = 36 - 40 = -4. Omdat de discriminant negatief is, N (X), en bijgevolg f (X), heeft geen echte wortels. De grafiek overschrijdt nooit de X-as. Als er nullen zijn gevonden, voegt u die punten toe aan de grafiek.  4 Zoek de verticale asymptoten. Een verticale asymptoot vindt plaats wanneer de noemer nul is. Instelling 4X + 2 = 0 geeft de verticale lijn X = -1/2. Geef elke verticale asymptoot een grafiek met een lichte of gestreepte lijn. Als een waarde van X maakt beide N (X) = 0 en D (X) = 0, er kan al dan niet een verticale asymptoot zijn. Dit is zeldzaam, maar zie de tips voor hoe ermee om te gaan als dit voorkomt.
4 Zoek de verticale asymptoten. Een verticale asymptoot vindt plaats wanneer de noemer nul is. Instelling 4X + 2 = 0 geeft de verticale lijn X = -1/2. Geef elke verticale asymptoot een grafiek met een lichte of gestreepte lijn. Als een waarde van X maakt beide N (X) = 0 en D (X) = 0, er kan al dan niet een verticale asymptoot zijn. Dit is zeldzaam, maar zie de tips voor hoe ermee om te gaan als dit voorkomt. 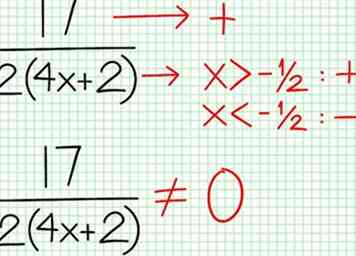 5 Kijk naar de rest van de divisie in stap 2. Wanneer is het positief, negatief of nul? In het voorbeeld is de teller van de rest 17, wat altijd positief is. De noemer, 4X + 2, is positief aan de rechterkant van de verticale asymptoot en negatief aan de linkerkant. Dit betekent dat de grafiek de lineaire asymptoot uit het bovenstaande benadert voor grote positieve waarden van X en van onderaf voor grote negatieve waarden van X. Sinds 17 / (8X + 4) kan nooit nul zijn, deze grafiek snijdt nooit de lijn Y = (1/2)X - (7/4). Voeg nu niets toe aan de grafiek, maar noteer deze conclusies voor later.
5 Kijk naar de rest van de divisie in stap 2. Wanneer is het positief, negatief of nul? In het voorbeeld is de teller van de rest 17, wat altijd positief is. De noemer, 4X + 2, is positief aan de rechterkant van de verticale asymptoot en negatief aan de linkerkant. Dit betekent dat de grafiek de lineaire asymptoot uit het bovenstaande benadert voor grote positieve waarden van X en van onderaf voor grote negatieve waarden van X. Sinds 17 / (8X + 4) kan nooit nul zijn, deze grafiek snijdt nooit de lijn Y = (1/2)X - (7/4). Voeg nu niets toe aan de grafiek, maar noteer deze conclusies voor later.  6 Zoek de lokale extrema. Een lokaal extremum kan optreden wanneer N '(X) D (X) - N (X) D '(X) = 0. In het voorbeeld, N '(X) = 4X - 6 en D '(X) = 4. N '(X) D (X) - N (X) D '(X) = (4X - 6)(4X + 2) - (2X2 - 6X + 5) * 4 = 0. Uitbreiden, termen combineren en delen door 4 bladeren X2 + X - 4 = 0. De kwadratische formule toont wortels in de buurt X = 3/2 en X = -5/2. (Deze verschillen ongeveer 0,06 van de exacte waarden, maar onze grafiek zal niet precies genoeg zijn om zich zorgen te maken over dat detailniveau. Het kiezen van een fatsoenlijke rationele benadering maakt de volgende stap eenvoudiger.)
6 Zoek de lokale extrema. Een lokaal extremum kan optreden wanneer N '(X) D (X) - N (X) D '(X) = 0. In het voorbeeld, N '(X) = 4X - 6 en D '(X) = 4. N '(X) D (X) - N (X) D '(X) = (4X - 6)(4X + 2) - (2X2 - 6X + 5) * 4 = 0. Uitbreiden, termen combineren en delen door 4 bladeren X2 + X - 4 = 0. De kwadratische formule toont wortels in de buurt X = 3/2 en X = -5/2. (Deze verschillen ongeveer 0,06 van de exacte waarden, maar onze grafiek zal niet precies genoeg zijn om zich zorgen te maken over dat detailniveau. Het kiezen van een fatsoenlijke rationele benadering maakt de volgende stap eenvoudiger.)  7 Vind de Y-waarden van elk lokaal extremum. Sluit de X-waarden van de vorige stap terug naar de oorspronkelijke rationale functie om het overeenkomstige te vinden Y-waarden. In het voorbeeld, f (3/2) = 1/16 en f (-5/2) = -65/16. Voeg deze punten (3/2, 1/16) en (-5/2, -65/16) toe aan de grafiek. Aangezien we in de vorige stap benaderd zijn, zijn dit niet de exacte minima en maxima, maar zijn ze waarschijnlijk dichtbij. (We weten (3/2, 1/16) ligt heel dicht bij het lokale minimum, vanaf stap 3 weten we dat Y is altijd positief wanneer X > -1/2 en we vonden een waarde zo klein als 1/16, dus althans in dit geval is de fout waarschijnlijk kleiner dan de dikte van de lijn.)
7 Vind de Y-waarden van elk lokaal extremum. Sluit de X-waarden van de vorige stap terug naar de oorspronkelijke rationale functie om het overeenkomstige te vinden Y-waarden. In het voorbeeld, f (3/2) = 1/16 en f (-5/2) = -65/16. Voeg deze punten (3/2, 1/16) en (-5/2, -65/16) toe aan de grafiek. Aangezien we in de vorige stap benaderd zijn, zijn dit niet de exacte minima en maxima, maar zijn ze waarschijnlijk dichtbij. (We weten (3/2, 1/16) ligt heel dicht bij het lokale minimum, vanaf stap 3 weten we dat Y is altijd positief wanneer X > -1/2 en we vonden een waarde zo klein als 1/16, dus althans in dit geval is de fout waarschijnlijk kleiner dan de dikte van de lijn.)  8 Verbind de punten en schuif de grafiek soepel uit van de bekende punten naar de asymptoten en zorg ervoor ze vanuit de juiste richting te benaderen. Zorg ervoor dat u de X-as behalve op de punten die je al bij stap 3 hebt gevonden. Steek de horizontale of lineaire asymptoot niet over, behalve bij de punten die je al in stap 5 hebt gevonden. Verander niet van opwaarts hellend naar schuin aflopend, behalve bij het uiterste in de vorige stap .
8 Verbind de punten en schuif de grafiek soepel uit van de bekende punten naar de asymptoten en zorg ervoor ze vanuit de juiste richting te benaderen. Zorg ervoor dat u de X-as behalve op de punten die je al bij stap 3 hebt gevonden. Steek de horizontale of lineaire asymptoot niet over, behalve bij de punten die je al in stap 5 hebt gevonden. Verander niet van opwaarts hellend naar schuin aflopend, behalve bij het uiterste in de vorige stap .