Een parabool is een tweedimensionale, spiegelsymmetrische curve die de vorm heeft van een boog. Elk punt op de parabool ligt op gelijke afstand van een vast punt (de focus) en een vaste rechte lijn (de richtlijn). Om een parabool in een grafiek te kunnen weergeven, moet je de vertex en verschillende punten aan beide kanten van de vertex vinden om het pad te markeren dat de punten afleggen.
Deel een van de twee:
Een parabool tekenen
-
 1 Begrijp de delen van een parabool. Mogelijk krijgt u bepaalde informatie voordat u begint en als u de terminologie kent, voorkomt u onnodige stappen. Hier zijn de delen van de parabool die je moet weten: [1]
1 Begrijp de delen van een parabool. Mogelijk krijgt u bepaalde informatie voordat u begint en als u de terminologie kent, voorkomt u onnodige stappen. Hier zijn de delen van de parabool die je moet weten: [1] - De focus. Een vast punt op het binnenste van de parabool dat wordt gebruikt voor de formele definitie van de curve.
- De richtlijn. Een vaste, rechte lijn. De parabool is de locus (serie) van punten waarin elk gegeven punt op gelijke afstand ligt van de focus en de directrice. (Zie het diagram hierboven.)
- De as van symmetrie. Dit is een rechte lijn die het keerpunt ("hoekpunt") van de parabool passeert en op gelijke afstand ligt van de corresponderende punten op de twee armen van de parabool.
- De top. Het punt waar de as van symmetrie de parabool doorkruist, wordt de top van de parabool genoemd. Als de parabool naar boven of naar rechts opent, is de vertex een minimum punt van de curve. Als het naar beneden of naar links opent, is de vertex een maximaal punt.
-
 2 Ken de vergelijking van een parabool. De algemene vergelijking van een parabool is y = bijl2+ bx + c. Het kan ook in de nog algemenere vorm worden geschreven y = a (x - h) ² + k, maar we zullen ons hier concentreren op de eerste vorm van de vergelijking.
2 Ken de vergelijking van een parabool. De algemene vergelijking van een parabool is y = bijl2+ bx + c. Het kan ook in de nog algemenere vorm worden geschreven y = a (x - h) ² + k, maar we zullen ons hier concentreren op de eerste vorm van de vergelijking. - Als de coëfficiënt een in de vergelijking is positief, de parabool opent naar boven (in een verticaal georiënteerde parabool), zoals de letter "U", en zijn top is een minimum punt. Als het een is negatief, de parabool opent naar beneden en heeft een top op het maximale punt. Als je dit moeilijk kunt onthouden, denk er dan zo over na: een vergelijking met een positief een waarde ziet eruit als een glimlach; een vergelijking met een negatief een waarde lijkt op een frons. [2]
- Laten we zeggen dat je de volgende vergelijking hebt: y = 2x2 -1. Deze parabool krijgt de vorm van een "U" omdat de een waarde (2) is positief.
- Als de vergelijking een kwadratische y-term heeft in plaats van een kwadraat x-term, wordt de parabool horizontaal georiënteerd en zijdelings geopend, naar rechts of links, zoals een "C" of een achterwaartse "C". Bijvoorbeeld de parabool y2 = x + 3 verschijnt aan de rechterkant, zoals een "C."
-
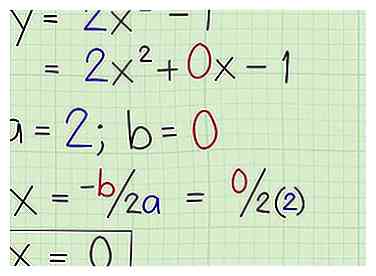 3 Zoek de symmetrieas. Onthoud dat de symmetrie-as de rechte lijn is die door het keerpunt (hoekpunt) van de parabool loopt. In het geval van een verticale parabool (openen of sluiten) is de as gelijk aan de x-coördinaat van de top, de x-waarde van het punt waar de symmetrieas de parabool passeert. Gebruik deze formule om de symmetrieas te vinden: x = -b / 2a. [3]
3 Zoek de symmetrieas. Onthoud dat de symmetrie-as de rechte lijn is die door het keerpunt (hoekpunt) van de parabool loopt. In het geval van een verticale parabool (openen of sluiten) is de as gelijk aan de x-coördinaat van de top, de x-waarde van het punt waar de symmetrieas de parabool passeert. Gebruik deze formule om de symmetrieas te vinden: x = -b / 2a. [3] - In het bovenstaande voorbeeld (y = 2x² -1), a = 2 en b = 0. Nu kun je de symmetrieas berekenen door de cijfers in te pluggen: x = -0 / (2) (2) = 0.
- In dit geval is de symmetrie-as x = 0 (wat de y-as van het coördinatenvlak is).
-
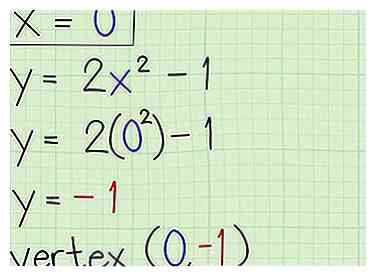 4 Vind de vertex. Zodra je de symmetrieas weet, kun je die waarde in x stoppen om de y-coördinaat te krijgen. Deze twee coördinaten zullen je de hoeksteen van de parabool geven. In dit geval zou u 0 in op 2x pluggen2 -1 om de y-coördinaat te krijgen. y = 2 x 02 -1 = 0 -1 = -1. De vertex is (0, -1) en de parabool kruist de y-as op -1. [4]
4 Vind de vertex. Zodra je de symmetrieas weet, kun je die waarde in x stoppen om de y-coördinaat te krijgen. Deze twee coördinaten zullen je de hoeksteen van de parabool geven. In dit geval zou u 0 in op 2x pluggen2 -1 om de y-coördinaat te krijgen. y = 2 x 02 -1 = 0 -1 = -1. De vertex is (0, -1) en de parabool kruist de y-as op -1. [4] - De coördinaten van de vertex zijn soms bekend als (h, k). In dit geval h is 0, en k is -1. De vergelijking voor de parabool kan in de vorm worden geschreven y = a (x - h) ² + k. In deze vorm is de vertex het punt (h, k) en u hoeft geen wiskunde uit te voeren om de vertex te vinden die de grafiek niet correct interpreteert.
-
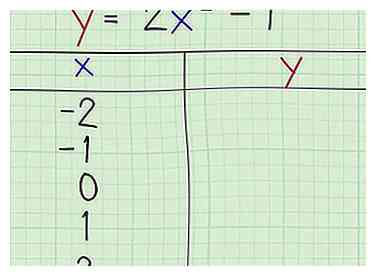 5 Stel een tabel samen met de gekozen waarden van x. Maak een tabel met bepaalde waarden van x in de eerste kolom. Deze tabel geeft u de coördinaten die u nodig hebt om de vergelijking in een grafiek weer te geven.
5 Stel een tabel samen met de gekozen waarden van x. Maak een tabel met bepaalde waarden van x in de eerste kolom. Deze tabel geeft u de coördinaten die u nodig hebt om de vergelijking in een grafiek weer te geven. - De middelste waarde van x moet de as van symmetrie zijn in het geval van een "verticale" parabool.
- U moet ten minste twee waarden boven en onder de middelste waarde voor x in de tabel opnemen omwille van de symmetrie.
- Plaats in dit voorbeeld de waarde van de symmetrieas (x = 0) in het midden van de tabel.
-
 6 Bereken de waarden van de bijbehorende y-coördinaten. Vervang elke waarde van x in de vergelijking van de parabool en bereken de bijbehorende waarden van y. Voeg deze berekende waarden van y in de tabel in. In dit voorbeeld worden de waarden van y als volgt berekend:
6 Bereken de waarden van de bijbehorende y-coördinaten. Vervang elke waarde van x in de vergelijking van de parabool en bereken de bijbehorende waarden van y. Voeg deze berekende waarden van y in de tabel in. In dit voorbeeld worden de waarden van y als volgt berekend: - Voor x = -2, y wordt berekend als: y = (2) (-2)2 - 1 = 8 - 1 = 7
- Voor x = -1, y wordt berekend als: y = (2) (-1)2 - 1 = 2 - 1 = 1
- Voor x = 0, y wordt berekend als: y = (2) (0)2 - 1 = 0 - 1 = -1
- Voor x = 1, y wordt berekend als: y = (2) (1)2 - 1 = 2 - 1 = 1
- Voor x = 2, y wordt berekend als: y = (2) (2)2 - 1 = 8 - 1 = 7
-
 7 Voeg de berekende waarden van y in de tabel in. Nu je minstens vijf coördinaatparen voor de parabool hebt gevonden, ben je bijna klaar om het in kaart te brengen. Op basis van je werk heb je nu de volgende punten: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Vergeet niet dat de parabool (symmetrisch) is gereflecteerd ten opzichte van de symmetrieas. Dit betekent dat de y-coördinaten van punten direct tegenover de symmetrieas van elkaar hetzelfde zijn. De y-coördinaten voor de x-coördinaten -2 en +2 zijn beide 7; de y-coördinaten voor de x-coördinaten -1 en +1 zijn beide 1, enzovoort.
7 Voeg de berekende waarden van y in de tabel in. Nu je minstens vijf coördinaatparen voor de parabool hebt gevonden, ben je bijna klaar om het in kaart te brengen. Op basis van je werk heb je nu de volgende punten: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Vergeet niet dat de parabool (symmetrisch) is gereflecteerd ten opzichte van de symmetrieas. Dit betekent dat de y-coördinaten van punten direct tegenover de symmetrieas van elkaar hetzelfde zijn. De y-coördinaten voor de x-coördinaten -2 en +2 zijn beide 7; de y-coördinaten voor de x-coördinaten -1 en +1 zijn beide 1, enzovoort. -
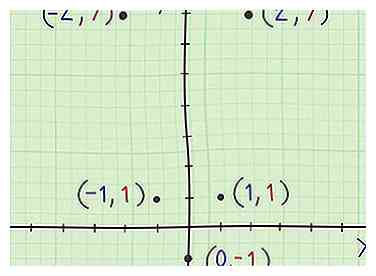 8 Zet de tabelpunten op het coördinatenvlak. Elke rij van de tabel vormt een coördinaatpaar (x, y) op het coördinatenvlak. Grafiek alle punten met behulp van de coördinaten in de tabel.
8 Zet de tabelpunten op het coördinatenvlak. Elke rij van de tabel vormt een coördinaatpaar (x, y) op het coördinatenvlak. Grafiek alle punten met behulp van de coördinaten in de tabel. - De x-as is horizontaal; de y-as is verticaal.
- De positieve getallen op de y-as liggen boven het punt (0, 0) en de negatieve getallen op de y-as liggen onder het punt (0, 0).
- De positieve getallen op de x-as staan rechts van het punt (0, 0) en de negatieve getallen op de x-as bevinden zich links van het punt (0, 0).
-
 9 Verbind de punten. Om de parabool in een grafiek weer te geven, verbindt u de punten die in de vorige stap zijn uitgezet. De grafiek in dit voorbeeld ziet eruit als een U. Verbind de punten met licht gebogen (in plaats van rechte) lijnen. Dit zorgt voor de meest nauwkeurige afbeelding van de parabool (die in zijn lengte ten minste enigszins gebogen is). Aan beide uiteinden van de parabool kunt u pijlen tekenen die van het hoekpunt weg wijzen als u dat wilt. Dit geeft aan dat de parabool voor onbepaalde tijd blijft bestaan. [5]
9 Verbind de punten. Om de parabool in een grafiek weer te geven, verbindt u de punten die in de vorige stap zijn uitgezet. De grafiek in dit voorbeeld ziet eruit als een U. Verbind de punten met licht gebogen (in plaats van rechte) lijnen. Dit zorgt voor de meest nauwkeurige afbeelding van de parabool (die in zijn lengte ten minste enigszins gebogen is). Aan beide uiteinden van de parabool kunt u pijlen tekenen die van het hoekpunt weg wijzen als u dat wilt. Dit geeft aan dat de parabool voor onbepaalde tijd blijft bestaan. [5]
Deel twee van twee:
De grafiek van een parabool verschuiven
Als je een snelkoppeling wilt voor het verschuiven van een parabool zonder dat je de top opnieuw hoeft te vinden en er meerdere punten op opnieuw moet plotten, moet je begrijpen hoe je de vergelijking van een parabool moet lezen en leren om hem verticaal of horizontaal te verschuiven. Begin met de basisparabool: y = x2. Dit heeft zijn hoekpunt op (0, 0) en opent naar boven. Punten erop zijn (-1, 1), (1, 1), (-2, 4) en (2, 4). Je kunt een parabool verplaatsen op basis van de vergelijking. [6]
-
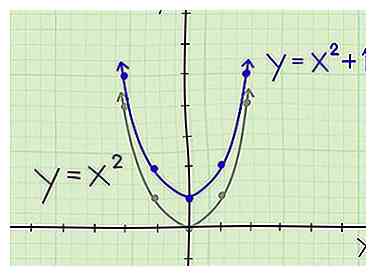 1 Verschuif een parabool omhoog. Overweeg de vergelijking y = x2 +1. Dit verschuift de originele parabool omhoog 1 eenheid. De vertex is nu (0, 1) in plaats van (0, 0). Het behoudt de exacte vorm van de originele parabool, maar elke y-coördinaat wordt 1 eenheid naar boven verschoven. Dus, in plaats van (-1, 1) en (1, 1), plotten we (-1, 2) en (1, 2).
1 Verschuif een parabool omhoog. Overweeg de vergelijking y = x2 +1. Dit verschuift de originele parabool omhoog 1 eenheid. De vertex is nu (0, 1) in plaats van (0, 0). Het behoudt de exacte vorm van de originele parabool, maar elke y-coördinaat wordt 1 eenheid naar boven verschoven. Dus, in plaats van (-1, 1) en (1, 1), plotten we (-1, 2) en (1, 2). -
 2 Verschuif een parabool naar beneden. Neem de vergelijking y = x2 -1. We verplaatsen de originele parabool 1 naar beneden, zodat de vertex nu (0, -1) is in plaats van (0, 0). Het heeft nog steeds dezelfde vorm als de oorspronkelijke parabool, maar elke y-coördinaat wordt 1 eenheid naar beneden verschoven. Dus, in plaats van (-1, 1) en (1, 1), bijvoorbeeld, plotten we (-1, 0) en (1, 0).
2 Verschuif een parabool naar beneden. Neem de vergelijking y = x2 -1. We verplaatsen de originele parabool 1 naar beneden, zodat de vertex nu (0, -1) is in plaats van (0, 0). Het heeft nog steeds dezelfde vorm als de oorspronkelijke parabool, maar elke y-coördinaat wordt 1 eenheid naar beneden verschoven. Dus, in plaats van (-1, 1) en (1, 1), bijvoorbeeld, plotten we (-1, 0) en (1, 0). -
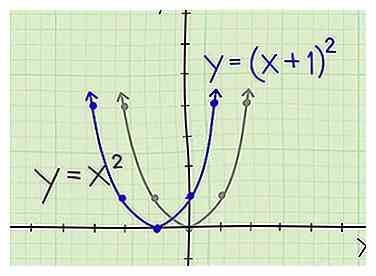 3 Verschuif een parabool naar links. Overweeg de vergelijking y = (x + 1)2. Hierdoor verschuift de originele parabool één eenheid naar links. De vertex is nu (-1, 0) in plaats van (0, 0). Het behoudt de vorm van de originele parabool, maar elke x-coördinaat wordt naar de linker eenheid geschoven. In plaats van (-1, 1) en (1, 1), bijvoorbeeld, plotten we (-2, 1) en (0, 1).
3 Verschuif een parabool naar links. Overweeg de vergelijking y = (x + 1)2. Hierdoor verschuift de originele parabool één eenheid naar links. De vertex is nu (-1, 0) in plaats van (0, 0). Het behoudt de vorm van de originele parabool, maar elke x-coördinaat wordt naar de linker eenheid geschoven. In plaats van (-1, 1) en (1, 1), bijvoorbeeld, plotten we (-2, 1) en (0, 1). -
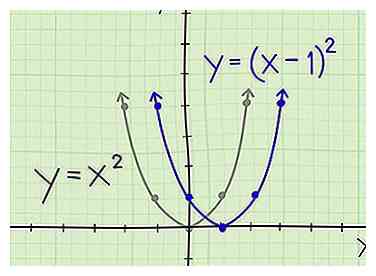 4 Verschuif een parabool naar rechts. Overweeg de vergelijking y = (x - 1)2. Dit is de originele parabool die één eenheid naar rechts is verschoven. De vertex is nu (1, 0) in plaats van (0, 0). Het behoudt de vorm van de originele parabool, maar elke x-coördinaat wordt naar de juiste eenheid verschoven. In plaats van (-1, 1) en (1, 1), bijvoorbeeld, plotten we (0, 1) en (2, 1).
4 Verschuif een parabool naar rechts. Overweeg de vergelijking y = (x - 1)2. Dit is de originele parabool die één eenheid naar rechts is verschoven. De vertex is nu (1, 0) in plaats van (0, 0). Het behoudt de vorm van de originele parabool, maar elke x-coördinaat wordt naar de juiste eenheid verschoven. In plaats van (-1, 1) en (1, 1), bijvoorbeeld, plotten we (0, 1) en (2, 1).
 Minotauromaquia
Minotauromaquia
 1 Begrijp de delen van een parabool. Mogelijk krijgt u bepaalde informatie voordat u begint en als u de terminologie kent, voorkomt u onnodige stappen. Hier zijn de delen van de parabool die je moet weten: [1]
1 Begrijp de delen van een parabool. Mogelijk krijgt u bepaalde informatie voordat u begint en als u de terminologie kent, voorkomt u onnodige stappen. Hier zijn de delen van de parabool die je moet weten: [1]  2 Ken de vergelijking van een parabool. De algemene vergelijking van een parabool is y = bijl2+ bx + c. Het kan ook in de nog algemenere vorm worden geschreven y = a (x - h) ² + k, maar we zullen ons hier concentreren op de eerste vorm van de vergelijking.
2 Ken de vergelijking van een parabool. De algemene vergelijking van een parabool is y = bijl2+ bx + c. Het kan ook in de nog algemenere vorm worden geschreven y = a (x - h) ² + k, maar we zullen ons hier concentreren op de eerste vorm van de vergelijking. 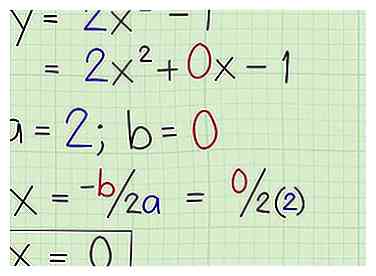 3 Zoek de symmetrieas. Onthoud dat de symmetrie-as de rechte lijn is die door het keerpunt (hoekpunt) van de parabool loopt. In het geval van een verticale parabool (openen of sluiten) is de as gelijk aan de x-coördinaat van de top, de x-waarde van het punt waar de symmetrieas de parabool passeert. Gebruik deze formule om de symmetrieas te vinden: x = -b / 2a. [3]
3 Zoek de symmetrieas. Onthoud dat de symmetrie-as de rechte lijn is die door het keerpunt (hoekpunt) van de parabool loopt. In het geval van een verticale parabool (openen of sluiten) is de as gelijk aan de x-coördinaat van de top, de x-waarde van het punt waar de symmetrieas de parabool passeert. Gebruik deze formule om de symmetrieas te vinden: x = -b / 2a. [3] 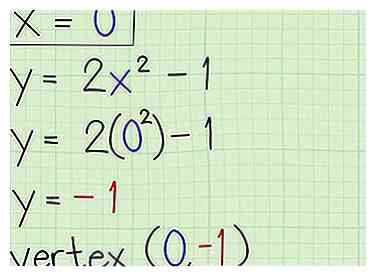 4 Vind de vertex. Zodra je de symmetrieas weet, kun je die waarde in x stoppen om de y-coördinaat te krijgen. Deze twee coördinaten zullen je de hoeksteen van de parabool geven. In dit geval zou u 0 in op 2x pluggen2 -1 om de y-coördinaat te krijgen. y = 2 x 02 -1 = 0 -1 = -1. De vertex is (0, -1) en de parabool kruist de y-as op -1. [4]
4 Vind de vertex. Zodra je de symmetrieas weet, kun je die waarde in x stoppen om de y-coördinaat te krijgen. Deze twee coördinaten zullen je de hoeksteen van de parabool geven. In dit geval zou u 0 in op 2x pluggen2 -1 om de y-coördinaat te krijgen. y = 2 x 02 -1 = 0 -1 = -1. De vertex is (0, -1) en de parabool kruist de y-as op -1. [4]  5 Stel een tabel samen met de gekozen waarden van x. Maak een tabel met bepaalde waarden van x in de eerste kolom. Deze tabel geeft u de coördinaten die u nodig hebt om de vergelijking in een grafiek weer te geven.
5 Stel een tabel samen met de gekozen waarden van x. Maak een tabel met bepaalde waarden van x in de eerste kolom. Deze tabel geeft u de coördinaten die u nodig hebt om de vergelijking in een grafiek weer te geven.  6 Bereken de waarden van de bijbehorende y-coördinaten. Vervang elke waarde van x in de vergelijking van de parabool en bereken de bijbehorende waarden van y. Voeg deze berekende waarden van y in de tabel in. In dit voorbeeld worden de waarden van y als volgt berekend:
6 Bereken de waarden van de bijbehorende y-coördinaten. Vervang elke waarde van x in de vergelijking van de parabool en bereken de bijbehorende waarden van y. Voeg deze berekende waarden van y in de tabel in. In dit voorbeeld worden de waarden van y als volgt berekend:  7 Voeg de berekende waarden van y in de tabel in. Nu je minstens vijf coördinaatparen voor de parabool hebt gevonden, ben je bijna klaar om het in kaart te brengen. Op basis van je werk heb je nu de volgende punten: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Vergeet niet dat de parabool (symmetrisch) is gereflecteerd ten opzichte van de symmetrieas. Dit betekent dat de y-coördinaten van punten direct tegenover de symmetrieas van elkaar hetzelfde zijn. De y-coördinaten voor de x-coördinaten -2 en +2 zijn beide 7; de y-coördinaten voor de x-coördinaten -1 en +1 zijn beide 1, enzovoort.
7 Voeg de berekende waarden van y in de tabel in. Nu je minstens vijf coördinaatparen voor de parabool hebt gevonden, ben je bijna klaar om het in kaart te brengen. Op basis van je werk heb je nu de volgende punten: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Vergeet niet dat de parabool (symmetrisch) is gereflecteerd ten opzichte van de symmetrieas. Dit betekent dat de y-coördinaten van punten direct tegenover de symmetrieas van elkaar hetzelfde zijn. De y-coördinaten voor de x-coördinaten -2 en +2 zijn beide 7; de y-coördinaten voor de x-coördinaten -1 en +1 zijn beide 1, enzovoort.  8 Zet de tabelpunten op het coördinatenvlak. Elke rij van de tabel vormt een coördinaatpaar (x, y) op het coördinatenvlak. Grafiek alle punten met behulp van de coördinaten in de tabel.
8 Zet de tabelpunten op het coördinatenvlak. Elke rij van de tabel vormt een coördinaatpaar (x, y) op het coördinatenvlak. Grafiek alle punten met behulp van de coördinaten in de tabel.  9 Verbind de punten. Om de parabool in een grafiek weer te geven, verbindt u de punten die in de vorige stap zijn uitgezet. De grafiek in dit voorbeeld ziet eruit als een U. Verbind de punten met licht gebogen (in plaats van rechte) lijnen. Dit zorgt voor de meest nauwkeurige afbeelding van de parabool (die in zijn lengte ten minste enigszins gebogen is). Aan beide uiteinden van de parabool kunt u pijlen tekenen die van het hoekpunt weg wijzen als u dat wilt. Dit geeft aan dat de parabool voor onbepaalde tijd blijft bestaan. [5]
9 Verbind de punten. Om de parabool in een grafiek weer te geven, verbindt u de punten die in de vorige stap zijn uitgezet. De grafiek in dit voorbeeld ziet eruit als een U. Verbind de punten met licht gebogen (in plaats van rechte) lijnen. Dit zorgt voor de meest nauwkeurige afbeelding van de parabool (die in zijn lengte ten minste enigszins gebogen is). Aan beide uiteinden van de parabool kunt u pijlen tekenen die van het hoekpunt weg wijzen als u dat wilt. Dit geeft aan dat de parabool voor onbepaalde tijd blijft bestaan. [5]  1 Verschuif een parabool omhoog. Overweeg de vergelijking y = x2 +1. Dit verschuift de originele parabool omhoog 1 eenheid. De vertex is nu (0, 1) in plaats van (0, 0). Het behoudt de exacte vorm van de originele parabool, maar elke y-coördinaat wordt 1 eenheid naar boven verschoven. Dus, in plaats van (-1, 1) en (1, 1), plotten we (-1, 2) en (1, 2).
1 Verschuif een parabool omhoog. Overweeg de vergelijking y = x2 +1. Dit verschuift de originele parabool omhoog 1 eenheid. De vertex is nu (0, 1) in plaats van (0, 0). Het behoudt de exacte vorm van de originele parabool, maar elke y-coördinaat wordt 1 eenheid naar boven verschoven. Dus, in plaats van (-1, 1) en (1, 1), plotten we (-1, 2) en (1, 2).  2 Verschuif een parabool naar beneden. Neem de vergelijking y = x2 -1. We verplaatsen de originele parabool 1 naar beneden, zodat de vertex nu (0, -1) is in plaats van (0, 0). Het heeft nog steeds dezelfde vorm als de oorspronkelijke parabool, maar elke y-coördinaat wordt 1 eenheid naar beneden verschoven. Dus, in plaats van (-1, 1) en (1, 1), bijvoorbeeld, plotten we (-1, 0) en (1, 0).
2 Verschuif een parabool naar beneden. Neem de vergelijking y = x2 -1. We verplaatsen de originele parabool 1 naar beneden, zodat de vertex nu (0, -1) is in plaats van (0, 0). Het heeft nog steeds dezelfde vorm als de oorspronkelijke parabool, maar elke y-coördinaat wordt 1 eenheid naar beneden verschoven. Dus, in plaats van (-1, 1) en (1, 1), bijvoorbeeld, plotten we (-1, 0) en (1, 0).  3 Verschuif een parabool naar links. Overweeg de vergelijking y = (x + 1)2. Hierdoor verschuift de originele parabool één eenheid naar links. De vertex is nu (-1, 0) in plaats van (0, 0). Het behoudt de vorm van de originele parabool, maar elke x-coördinaat wordt naar de linker eenheid geschoven. In plaats van (-1, 1) en (1, 1), bijvoorbeeld, plotten we (-2, 1) en (0, 1).
3 Verschuif een parabool naar links. Overweeg de vergelijking y = (x + 1)2. Hierdoor verschuift de originele parabool één eenheid naar links. De vertex is nu (-1, 0) in plaats van (0, 0). Het behoudt de vorm van de originele parabool, maar elke x-coördinaat wordt naar de linker eenheid geschoven. In plaats van (-1, 1) en (1, 1), bijvoorbeeld, plotten we (-2, 1) en (0, 1).  4 Verschuif een parabool naar rechts. Overweeg de vergelijking y = (x - 1)2. Dit is de originele parabool die één eenheid naar rechts is verschoven. De vertex is nu (1, 0) in plaats van (0, 0). Het behoudt de vorm van de originele parabool, maar elke x-coördinaat wordt naar de juiste eenheid verschoven. In plaats van (-1, 1) en (1, 1), bijvoorbeeld, plotten we (0, 1) en (2, 1).
4 Verschuif een parabool naar rechts. Overweeg de vergelijking y = (x - 1)2. Dit is de originele parabool die één eenheid naar rechts is verschoven. De vertex is nu (1, 0) in plaats van (0, 0). Het behoudt de vorm van de originele parabool, maar elke x-coördinaat wordt naar de juiste eenheid verschoven. In plaats van (-1, 1) en (1, 1), bijvoorbeeld, plotten we (0, 1) en (2, 1).