De top van een kwadratische vergelijking of parabool is het hoogste of laagste punt van die vergelijking. Het ligt ook op het vlak van symmetrie van de hele parabool; wat links van de parabool ligt, is een compleet spiegelbeeld van alles wat rechts staat. Als u de top van een kwadratische vergelijking wilt vinden, kunt u de vertexformule gebruiken of het vierkant invullen.
Methode één van de twee:
De Vertex-formule gebruiken
-
 1 Identificeer de waarden van a, b en c. In een kwadratische vergelijking, de X2 term = een, de X term = b, en de constante term (de term zonder een variabele) = c. Laten we zeggen dat je met de volgende vergelijking werkt: Y = X2 + 9x + 18. In dit voorbeeld een = 1, b = 9, en c = 18.[1]
1 Identificeer de waarden van a, b en c. In een kwadratische vergelijking, de X2 term = een, de X term = b, en de constante term (de term zonder een variabele) = c. Laten we zeggen dat je met de volgende vergelijking werkt: Y = X2 + 9x + 18. In dit voorbeeld een = 1, b = 9, en c = 18.[1] -
 2 Gebruik de vertex-formule om de x-waarde van de vertex te vinden. De vertex is ook de symmetrieas van de vergelijking. De formule voor het vinden van de x-waarde van de top van een kwadratische vergelijking is x = -b / 2a. Sluit de relevante waarden in om te vinden X. Vervang de waarden voor a en b. Laat je werk zien:
2 Gebruik de vertex-formule om de x-waarde van de vertex te vinden. De vertex is ook de symmetrieas van de vergelijking. De formule voor het vinden van de x-waarde van de top van een kwadratische vergelijking is x = -b / 2a. Sluit de relevante waarden in om te vinden X. Vervang de waarden voor a en b. Laat je werk zien: - x = -b / 2a
- x = - (9) / (2) (1)
- x = -9/2
-
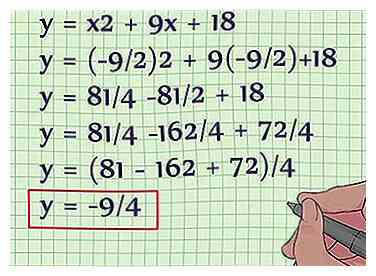 3 Steek de x-waarde in de oorspronkelijke vergelijking om de y-waarde te krijgen. Nu dat je de x-waarde kent, plug je hem gewoon in op de originele formule voor de y-waarde. Je kunt de formule bedenken om de top van een kwadratische functie als zijnde te vinden (x, y) = [(-b / 2a), f (-b / 2a)]. Dit betekent alleen dat om de y-waarde te verkrijgen, u de x-waarde op basis van de formule moet vinden en vervolgens weer in de vergelijking moet stoppen. Hier is hoe je het doet:
3 Steek de x-waarde in de oorspronkelijke vergelijking om de y-waarde te krijgen. Nu dat je de x-waarde kent, plug je hem gewoon in op de originele formule voor de y-waarde. Je kunt de formule bedenken om de top van een kwadratische functie als zijnde te vinden (x, y) = [(-b / 2a), f (-b / 2a)]. Dit betekent alleen dat om de y-waarde te verkrijgen, u de x-waarde op basis van de formule moet vinden en vervolgens weer in de vergelijking moet stoppen. Hier is hoe je het doet: - y = x2 + 9x + 18
- y = (-9/2)2 + 9(-9/2) +18
- y = 81/4 -81/2 + 18
- y = 81/4 -162/4 + 72/4
- y = (81 - 162 + 72) / 4
- y = -9/4
-
 4 Noteer de x- en y-waarden als een geordend paar. Nu dat u weet dat x = -9/2, en y = -9/4, noteer ze gewoon als een geordend paar: (-9/2, -9/4). De top van deze kwadratische vergelijking is (-9/2, -9/4). Als je deze parabool in een grafiek zou tekenen, zou dit punt het minimum van de parabool zijn, omdat de x2 termijn is positief.
4 Noteer de x- en y-waarden als een geordend paar. Nu dat u weet dat x = -9/2, en y = -9/4, noteer ze gewoon als een geordend paar: (-9/2, -9/4). De top van deze kwadratische vergelijking is (-9/2, -9/4). Als je deze parabool in een grafiek zou tekenen, zou dit punt het minimum van de parabool zijn, omdat de x2 termijn is positief.
Methode twee van twee:
Het vierkant voltooien
-
 1 Noteer de vergelijking. Het invullen van het vierkant is een andere manier om de top van een kwadratische vergelijking te vinden. Voor deze methode kun je, wanneer je het einde hebt bereikt, meteen je x- en y-coördinaten vinden in plaats van de x-coördinaat weer in te pluggen in de oorspronkelijke vergelijking. Laten we zeggen dat je met de volgende kwadratische vergelijking werkt: X2 + 4x + 1 = 0.[2]
1 Noteer de vergelijking. Het invullen van het vierkant is een andere manier om de top van een kwadratische vergelijking te vinden. Voor deze methode kun je, wanneer je het einde hebt bereikt, meteen je x- en y-coördinaten vinden in plaats van de x-coördinaat weer in te pluggen in de oorspronkelijke vergelijking. Laten we zeggen dat je met de volgende kwadratische vergelijking werkt: X2 + 4x + 1 = 0.[2] -
 2 Verdeel elke term door de coëfficiënt van de x 2-term. In dit geval is de coëfficiënt van de x 2-term 1, dus u kunt deze stap overslaan. Het verdelen van elke term met 1 zou niets veranderen. Door elke term te delen door 0, verandert alles.
2 Verdeel elke term door de coëfficiënt van de x 2-term. In dit geval is de coëfficiënt van de x 2-term 1, dus u kunt deze stap overslaan. Het verdelen van elke term met 1 zou niets veranderen. Door elke term te delen door 0, verandert alles. -
 3 Verplaats de constante term naar de rechterkant van de vergelijking. De constante term is de term zonder een coëfficiënt. In dit geval is het "1". Verplaats 1 naar de andere kant van de vergelijking door 1 van beide kanten af te trekken. Hier is hoe je het doet:[3]
3 Verplaats de constante term naar de rechterkant van de vergelijking. De constante term is de term zonder een coëfficiënt. In dit geval is het "1". Verplaats 1 naar de andere kant van de vergelijking door 1 van beide kanten af te trekken. Hier is hoe je het doet:[3] - X2 + 4x + 1 = 0
- X2 + 4x + 1 -1 = 0 - 1
- X2 + 4x = - 1
-
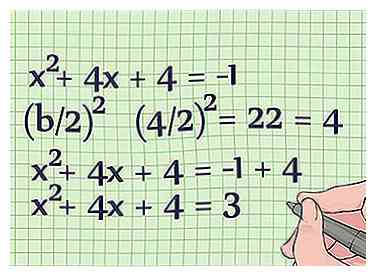 4 Voltooi het vierkant aan de linkerkant van de vergelijking. Om dit te doen, vind je gewoon (B / 2)2 en voeg het resultaat toe aan beide zijden van de vergelijking. Sluit "4" aan voor b, omdat "4x" de b-term is van deze vergelijking.
4 Voltooi het vierkant aan de linkerkant van de vergelijking. Om dit te doen, vind je gewoon (B / 2)2 en voeg het resultaat toe aan beide zijden van de vergelijking. Sluit "4" aan voor b, omdat "4x" de b-term is van deze vergelijking. - (4/2)2 = 22 = 4. Voeg nu 4 aan beide kanten van de vergelijking toe om het volgende te krijgen:
- X2 + 4x + 4 = -1 + 4
- X2 + 4x + 4 = 3
- (4/2)2 = 22 = 4. Voeg nu 4 aan beide kanten van de vergelijking toe om het volgende te krijgen:
-
 5 Factor de linkerkant van de vergelijking. Nu zul je dat zien x2 + 4x + 4 is een perfect vierkant. Het kan worden herschreven als (x + 2)2 = 3
5 Factor de linkerkant van de vergelijking. Nu zul je dat zien x2 + 4x + 4 is een perfect vierkant. Het kan worden herschreven als (x + 2)2 = 3 - 6 Gebruik dit formaat om de x- en y-coördinaten te vinden. Je kunt je x-coördinaat vinden door eenvoudigweg (x + 2) 2 gelijk aan nul te zetten. Dus wanneer (x + 2) 2 = 0, wat zou x moeten zijn? De variabele x zou -2 moeten zijn om de +2 uit te balanceren, dus je x-coördinaat is -2. Je y-coördinaat is simpelweg de constante term aan de andere kant van de vergelijking. Dus, y = 3. Je kunt ook een snelkoppeling doen en gewoon het tegenovergestelde teken van het getal tussen haakjes nemen om de x-coördinaat te krijgen. Dus de vertex van de vergelijking x2 + 4x + 1 = (-2, -3)
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Identificeer de waarden van a, b en c. In een kwadratische vergelijking, de X2 term = een, de X term = b, en de constante term (de term zonder een variabele) = c. Laten we zeggen dat je met de volgende vergelijking werkt: Y = X2 + 9x + 18. In dit voorbeeld een = 1, b = 9, en c = 18.[1]
1 Identificeer de waarden van a, b en c. In een kwadratische vergelijking, de X2 term = een, de X term = b, en de constante term (de term zonder een variabele) = c. Laten we zeggen dat je met de volgende vergelijking werkt: Y = X2 + 9x + 18. In dit voorbeeld een = 1, b = 9, en c = 18.[1]  2 Gebruik de vertex-formule om de x-waarde van de vertex te vinden. De vertex is ook de symmetrieas van de vergelijking. De formule voor het vinden van de x-waarde van de top van een kwadratische vergelijking is x = -b / 2a. Sluit de relevante waarden in om te vinden X. Vervang de waarden voor a en b. Laat je werk zien:
2 Gebruik de vertex-formule om de x-waarde van de vertex te vinden. De vertex is ook de symmetrieas van de vergelijking. De formule voor het vinden van de x-waarde van de top van een kwadratische vergelijking is x = -b / 2a. Sluit de relevante waarden in om te vinden X. Vervang de waarden voor a en b. Laat je werk zien: 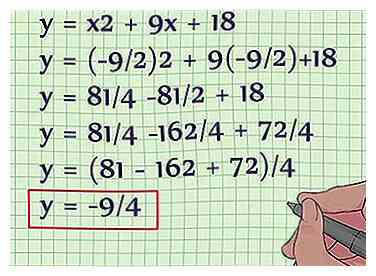 3 Steek de x-waarde in de oorspronkelijke vergelijking om de y-waarde te krijgen. Nu dat je de x-waarde kent, plug je hem gewoon in op de originele formule voor de y-waarde. Je kunt de formule bedenken om de top van een kwadratische functie als zijnde te vinden (x, y) = [(-b / 2a), f (-b / 2a)]. Dit betekent alleen dat om de y-waarde te verkrijgen, u de x-waarde op basis van de formule moet vinden en vervolgens weer in de vergelijking moet stoppen. Hier is hoe je het doet:
3 Steek de x-waarde in de oorspronkelijke vergelijking om de y-waarde te krijgen. Nu dat je de x-waarde kent, plug je hem gewoon in op de originele formule voor de y-waarde. Je kunt de formule bedenken om de top van een kwadratische functie als zijnde te vinden (x, y) = [(-b / 2a), f (-b / 2a)]. Dit betekent alleen dat om de y-waarde te verkrijgen, u de x-waarde op basis van de formule moet vinden en vervolgens weer in de vergelijking moet stoppen. Hier is hoe je het doet:  4 Noteer de x- en y-waarden als een geordend paar. Nu dat u weet dat x = -9/2, en y = -9/4, noteer ze gewoon als een geordend paar: (-9/2, -9/4). De top van deze kwadratische vergelijking is (-9/2, -9/4). Als je deze parabool in een grafiek zou tekenen, zou dit punt het minimum van de parabool zijn, omdat de x2 termijn is positief.
4 Noteer de x- en y-waarden als een geordend paar. Nu dat u weet dat x = -9/2, en y = -9/4, noteer ze gewoon als een geordend paar: (-9/2, -9/4). De top van deze kwadratische vergelijking is (-9/2, -9/4). Als je deze parabool in een grafiek zou tekenen, zou dit punt het minimum van de parabool zijn, omdat de x2 termijn is positief.  1 Noteer de vergelijking. Het invullen van het vierkant is een andere manier om de top van een kwadratische vergelijking te vinden. Voor deze methode kun je, wanneer je het einde hebt bereikt, meteen je x- en y-coördinaten vinden in plaats van de x-coördinaat weer in te pluggen in de oorspronkelijke vergelijking. Laten we zeggen dat je met de volgende kwadratische vergelijking werkt: X2 + 4x + 1 = 0.[2]
1 Noteer de vergelijking. Het invullen van het vierkant is een andere manier om de top van een kwadratische vergelijking te vinden. Voor deze methode kun je, wanneer je het einde hebt bereikt, meteen je x- en y-coördinaten vinden in plaats van de x-coördinaat weer in te pluggen in de oorspronkelijke vergelijking. Laten we zeggen dat je met de volgende kwadratische vergelijking werkt: X2 + 4x + 1 = 0.[2]  2 Verdeel elke term door de coëfficiënt van de x 2-term. In dit geval is de coëfficiënt van de x 2-term 1, dus u kunt deze stap overslaan. Het verdelen van elke term met 1 zou niets veranderen. Door elke term te delen door 0, verandert alles.
2 Verdeel elke term door de coëfficiënt van de x 2-term. In dit geval is de coëfficiënt van de x 2-term 1, dus u kunt deze stap overslaan. Het verdelen van elke term met 1 zou niets veranderen. Door elke term te delen door 0, verandert alles.  3 Verplaats de constante term naar de rechterkant van de vergelijking. De constante term is de term zonder een coëfficiënt. In dit geval is het "1". Verplaats 1 naar de andere kant van de vergelijking door 1 van beide kanten af te trekken. Hier is hoe je het doet:[3]
3 Verplaats de constante term naar de rechterkant van de vergelijking. De constante term is de term zonder een coëfficiënt. In dit geval is het "1". Verplaats 1 naar de andere kant van de vergelijking door 1 van beide kanten af te trekken. Hier is hoe je het doet:[3] 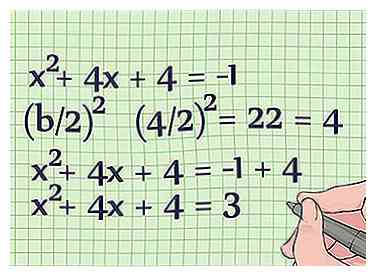 4 Voltooi het vierkant aan de linkerkant van de vergelijking. Om dit te doen, vind je gewoon (B / 2)2 en voeg het resultaat toe aan beide zijden van de vergelijking. Sluit "4" aan voor b, omdat "4x" de b-term is van deze vergelijking.
4 Voltooi het vierkant aan de linkerkant van de vergelijking. Om dit te doen, vind je gewoon (B / 2)2 en voeg het resultaat toe aan beide zijden van de vergelijking. Sluit "4" aan voor b, omdat "4x" de b-term is van deze vergelijking.  5 Factor de linkerkant van de vergelijking. Nu zul je dat zien x2 + 4x + 4 is een perfect vierkant. Het kan worden herschreven als (x + 2)2 = 3
5 Factor de linkerkant van de vergelijking. Nu zul je dat zien x2 + 4x + 4 is een perfect vierkant. Het kan worden herschreven als (x + 2)2 = 3