Een middelloodlijn is een lijn die een lijnsegment met twee punten precies doormidden snijdt met een hoek van 90 graden. Om de middelloodlijn van twee punten te vinden, hoeft u alleen hun middelpunt en negatieve reciprook te vinden en deze antwoorden in de vergelijking in te voegen voor een lijn in de vorm van een hellingsonderbreking. Als u wilt weten hoe u de middelloodlijn van twee punten kunt vinden, volgt u deze stappen.
Methode één van de twee:
Informatie verzamelen
-
 1 Zoek het middelpunt van de twee punten. Om het middelpunt van twee punten te vinden, sluit u eenvoudigweg de middelpuntformule aan: [(X1 + x2) / 2, (y1 + y2)/2]. Dit betekent dat je alleen het gemiddelde van de x- en y-coördinaten van de twee sets punten vindt, wat je naar het middelpunt van de twee coördinaten leidt. Laten we zeggen dat we met de (x1, y1) coördinaten van (2, 5) en de (x2, y2) coördinaten van (8, 3). Hier is hoe je het middelpunt vindt voor die twee punten:[1]
1 Zoek het middelpunt van de twee punten. Om het middelpunt van twee punten te vinden, sluit u eenvoudigweg de middelpuntformule aan: [(X1 + x2) / 2, (y1 + y2)/2]. Dit betekent dat je alleen het gemiddelde van de x- en y-coördinaten van de twee sets punten vindt, wat je naar het middelpunt van de twee coördinaten leidt. Laten we zeggen dat we met de (x1, y1) coördinaten van (2, 5) en de (x2, y2) coördinaten van (8, 3). Hier is hoe je het middelpunt vindt voor die twee punten:[1] - [(2+8)/2, (5 +3)/2] =
- (10/2, 8/2) =
- (5, 4)
- De coördinaten van het middelpunt van (2, 5) en (8, 3) zijn (5, 4).
-
 2 Zoek de helling van de twee punten. Om de helling van de twee punten te vinden, koppelt u gewoon de punten in de hellingformule: (y2 - y1) / (x2 - x1). De helling van een lijn meet de afstand van de verticale verandering over de afstand van de horizontale verandering. Zo kun je de helling van de lijn vinden die door de punten gaat (2, 5) en (8, 3):[2]
2 Zoek de helling van de twee punten. Om de helling van de twee punten te vinden, koppelt u gewoon de punten in de hellingformule: (y2 - y1) / (x2 - x1). De helling van een lijn meet de afstand van de verticale verandering over de afstand van de horizontale verandering. Zo kun je de helling van de lijn vinden die door de punten gaat (2, 5) en (8, 3):[2] - (3-5)/(8-2) =
- -2/6 =
- -1/3
- De helling van de lijn is -1/3. Om deze helling te vinden, moet je 2/6 terugbrengen tot de laagste waarden, 1/3, omdat zowel 2 als 6 gelijk verdeeld zijn door 2.
-
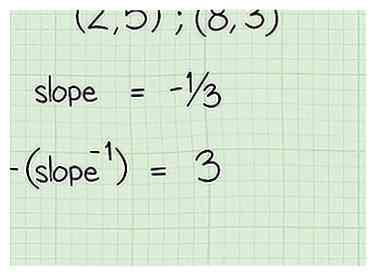 3 Zoek de negatieve reciproque van de helling van de twee punten. Om de negatieve reciproque van een helling te vinden, neemt u gewoon de omgekeerde helling en verandert u het teken. Je kunt de reciprook van een getal eenvoudigweg nemen door de x- en y-coördinaten om te draaien. De reciproke van 1/2 is -2/1, of slechts -2; de reciproke van -4 is 1/4.[3]
3 Zoek de negatieve reciproque van de helling van de twee punten. Om de negatieve reciproque van een helling te vinden, neemt u gewoon de omgekeerde helling en verandert u het teken. Je kunt de reciprook van een getal eenvoudigweg nemen door de x- en y-coördinaten om te draaien. De reciproke van 1/2 is -2/1, of slechts -2; de reciproke van -4 is 1/4.[3] - De negatieve reciproke waarde van -1/3 is 3 omdat 3/1 de reciproque is van 1/3 en het teken is veranderd van negatief in positief.
Methode twee van twee:
Berekening van de vergelijking van de lijn
-
 1 Schrijf de vergelijking van een lijn in het hellingsintercept. De vergelijking van een lijn in hellingsintercept vorm is y = mx + b waarbij elke x- en y-coördinaten in de regel worden weergegeven door de "x" en "y", de "m" vertegenwoordigt de helling van de lijn en de "b" vertegenwoordigt het y-snijpunt van de lijn. Het y-snijpunt is waar de lijn de y-as snijdt. Nadat u deze vergelijking hebt genoteerd, kunt u beginnen met het vinden van de vergelijking van de middelloodlijn van de twee punten.[4]
1 Schrijf de vergelijking van een lijn in het hellingsintercept. De vergelijking van een lijn in hellingsintercept vorm is y = mx + b waarbij elke x- en y-coördinaten in de regel worden weergegeven door de "x" en "y", de "m" vertegenwoordigt de helling van de lijn en de "b" vertegenwoordigt het y-snijpunt van de lijn. Het y-snijpunt is waar de lijn de y-as snijdt. Nadat u deze vergelijking hebt genoteerd, kunt u beginnen met het vinden van de vergelijking van de middelloodlijn van de twee punten.[4] -
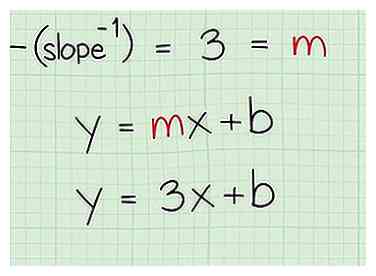 2 Steek de negatieve reciproque van de oorspronkelijke helling in de vergelijking. De negatieve reciproke van de helling van de punten (2, 5) en (8, 3) was 3. De "m" in de vergelijking vertegenwoordigt de helling, dus plug de 3 in de "m" in de vergelijking van y = mx + b.
2 Steek de negatieve reciproque van de oorspronkelijke helling in de vergelijking. De negatieve reciproke van de helling van de punten (2, 5) en (8, 3) was 3. De "m" in de vergelijking vertegenwoordigt de helling, dus plug de 3 in de "m" in de vergelijking van y = mx + b. - 3 -> y = mx + b =
- y = 3x + b
-
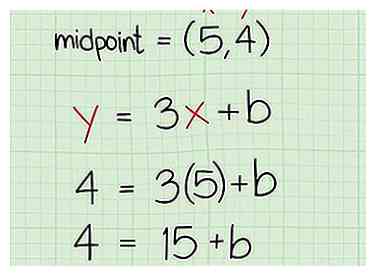 3 Steek de punten van het middelpunt in de lijn. Je weet al dat het middelpunt van de punten (2, 5) en (8, 3) (5, 4) is. Aangezien de middelloodlijn door het middelpunt van de twee lijnen loopt, kunt u de coördinaten van het middelpunt in de vergelijking van de lijn invoegen. Sluit eenvoudig (5, 4) aan op de x- en y-coördinaten van de lijn.
3 Steek de punten van het middelpunt in de lijn. Je weet al dat het middelpunt van de punten (2, 5) en (8, 3) (5, 4) is. Aangezien de middelloodlijn door het middelpunt van de twee lijnen loopt, kunt u de coördinaten van het middelpunt in de vergelijking van de lijn invoegen. Sluit eenvoudig (5, 4) aan op de x- en y-coördinaten van de lijn. - (5, 4) ---> y = 3x + b =
- 4 = 3 (5) + b =
- 4 = 15 + b
-
 4 Los op voor het snijpunt. U hebt drie van de vier variabelen gevonden in de vergelijking van de regel. Nu heb je genoeg informatie om op te lossen voor de resterende variabele, "b", wat het y-snijpunt van deze regel is. Isoleer eenvoudig de variabele "b" om de waarde ervan te vinden. Trek 15 van beide kanten van de vergelijking af.
4 Los op voor het snijpunt. U hebt drie van de vier variabelen gevonden in de vergelijking van de regel. Nu heb je genoeg informatie om op te lossen voor de resterende variabele, "b", wat het y-snijpunt van deze regel is. Isoleer eenvoudig de variabele "b" om de waarde ervan te vinden. Trek 15 van beide kanten van de vergelijking af. - 4 = 15 + b =
- -11 = b
- b = -11
-
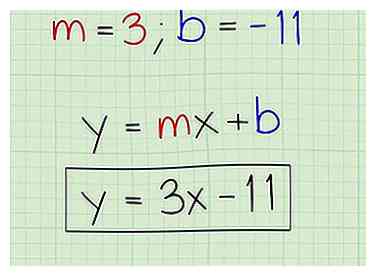 5 Schrijf de vergelijking van de middelloodlijn. Om de vergelijking van de middelloodlijn te schrijven, hoeft u alleen maar de helling van de lijn (3) en het y-snijpunt (-11) in te voegen in de vergelijking van een lijn in de vorm van hellingsonderbreking. U mag geen termen in de x- en y-coördinaten invoegen, omdat u met deze vergelijking elke coördinaat op de regel kunt vinden door een willekeurige x- of y-coördinaat in te voegen.
5 Schrijf de vergelijking van de middelloodlijn. Om de vergelijking van de middelloodlijn te schrijven, hoeft u alleen maar de helling van de lijn (3) en het y-snijpunt (-11) in te voegen in de vergelijking van een lijn in de vorm van hellingsonderbreking. U mag geen termen in de x- en y-coördinaten invoegen, omdat u met deze vergelijking elke coördinaat op de regel kunt vinden door een willekeurige x- of y-coördinaat in te voegen. - y = mx + b
- y = 3x - 11
- De vergelijking voor de middelloodlijn van de punten (2, 5) en (8, 3) is y = 3x - 11.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Zoek het middelpunt van de twee punten. Om het middelpunt van twee punten te vinden, sluit u eenvoudigweg de middelpuntformule aan: [(X1 + x2) / 2, (y1 + y2)/2]. Dit betekent dat je alleen het gemiddelde van de x- en y-coördinaten van de twee sets punten vindt, wat je naar het middelpunt van de twee coördinaten leidt. Laten we zeggen dat we met de (x1, y1) coördinaten van (2, 5) en de (x2, y2) coördinaten van (8, 3). Hier is hoe je het middelpunt vindt voor die twee punten:[1]
1 Zoek het middelpunt van de twee punten. Om het middelpunt van twee punten te vinden, sluit u eenvoudigweg de middelpuntformule aan: [(X1 + x2) / 2, (y1 + y2)/2]. Dit betekent dat je alleen het gemiddelde van de x- en y-coördinaten van de twee sets punten vindt, wat je naar het middelpunt van de twee coördinaten leidt. Laten we zeggen dat we met de (x1, y1) coördinaten van (2, 5) en de (x2, y2) coördinaten van (8, 3). Hier is hoe je het middelpunt vindt voor die twee punten:[1]  2 Zoek de helling van de twee punten. Om de helling van de twee punten te vinden, koppelt u gewoon de punten in de hellingformule: (y2 - y1) / (x2 - x1). De helling van een lijn meet de afstand van de verticale verandering over de afstand van de horizontale verandering. Zo kun je de helling van de lijn vinden die door de punten gaat (2, 5) en (8, 3):[2]
2 Zoek de helling van de twee punten. Om de helling van de twee punten te vinden, koppelt u gewoon de punten in de hellingformule: (y2 - y1) / (x2 - x1). De helling van een lijn meet de afstand van de verticale verandering over de afstand van de horizontale verandering. Zo kun je de helling van de lijn vinden die door de punten gaat (2, 5) en (8, 3):[2] 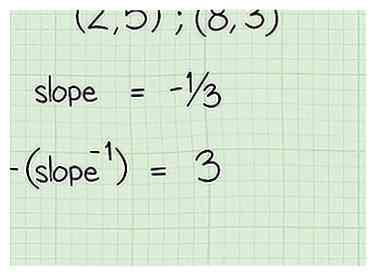 3 Zoek de negatieve reciproque van de helling van de twee punten. Om de negatieve reciproque van een helling te vinden, neemt u gewoon de omgekeerde helling en verandert u het teken. Je kunt de reciprook van een getal eenvoudigweg nemen door de x- en y-coördinaten om te draaien. De reciproke van 1/2 is -2/1, of slechts -2; de reciproke van -4 is 1/4.[3]
3 Zoek de negatieve reciproque van de helling van de twee punten. Om de negatieve reciproque van een helling te vinden, neemt u gewoon de omgekeerde helling en verandert u het teken. Je kunt de reciprook van een getal eenvoudigweg nemen door de x- en y-coördinaten om te draaien. De reciproke van 1/2 is -2/1, of slechts -2; de reciproke van -4 is 1/4.[3]  1 Schrijf de vergelijking van een lijn in het hellingsintercept. De vergelijking van een lijn in hellingsintercept vorm is y = mx + b waarbij elke x- en y-coördinaten in de regel worden weergegeven door de "x" en "y", de "m" vertegenwoordigt de helling van de lijn en de "b" vertegenwoordigt het y-snijpunt van de lijn. Het y-snijpunt is waar de lijn de y-as snijdt. Nadat u deze vergelijking hebt genoteerd, kunt u beginnen met het vinden van de vergelijking van de middelloodlijn van de twee punten.[4]
1 Schrijf de vergelijking van een lijn in het hellingsintercept. De vergelijking van een lijn in hellingsintercept vorm is y = mx + b waarbij elke x- en y-coördinaten in de regel worden weergegeven door de "x" en "y", de "m" vertegenwoordigt de helling van de lijn en de "b" vertegenwoordigt het y-snijpunt van de lijn. Het y-snijpunt is waar de lijn de y-as snijdt. Nadat u deze vergelijking hebt genoteerd, kunt u beginnen met het vinden van de vergelijking van de middelloodlijn van de twee punten.[4] 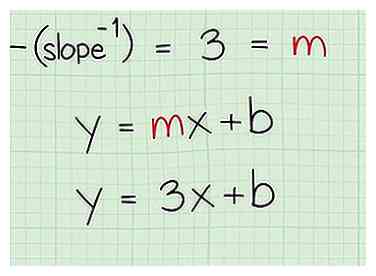 2 Steek de negatieve reciproque van de oorspronkelijke helling in de vergelijking. De negatieve reciproke van de helling van de punten (2, 5) en (8, 3) was 3. De "m" in de vergelijking vertegenwoordigt de helling, dus plug de 3 in de "m" in de vergelijking van y = mx + b.
2 Steek de negatieve reciproque van de oorspronkelijke helling in de vergelijking. De negatieve reciproke van de helling van de punten (2, 5) en (8, 3) was 3. De "m" in de vergelijking vertegenwoordigt de helling, dus plug de 3 in de "m" in de vergelijking van y = mx + b. 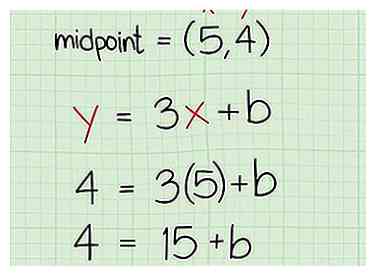 3 Steek de punten van het middelpunt in de lijn. Je weet al dat het middelpunt van de punten (2, 5) en (8, 3) (5, 4) is. Aangezien de middelloodlijn door het middelpunt van de twee lijnen loopt, kunt u de coördinaten van het middelpunt in de vergelijking van de lijn invoegen. Sluit eenvoudig (5, 4) aan op de x- en y-coördinaten van de lijn.
3 Steek de punten van het middelpunt in de lijn. Je weet al dat het middelpunt van de punten (2, 5) en (8, 3) (5, 4) is. Aangezien de middelloodlijn door het middelpunt van de twee lijnen loopt, kunt u de coördinaten van het middelpunt in de vergelijking van de lijn invoegen. Sluit eenvoudig (5, 4) aan op de x- en y-coördinaten van de lijn.  4 Los op voor het snijpunt. U hebt drie van de vier variabelen gevonden in de vergelijking van de regel. Nu heb je genoeg informatie om op te lossen voor de resterende variabele, "b", wat het y-snijpunt van deze regel is. Isoleer eenvoudig de variabele "b" om de waarde ervan te vinden. Trek 15 van beide kanten van de vergelijking af.
4 Los op voor het snijpunt. U hebt drie van de vier variabelen gevonden in de vergelijking van de regel. Nu heb je genoeg informatie om op te lossen voor de resterende variabele, "b", wat het y-snijpunt van deze regel is. Isoleer eenvoudig de variabele "b" om de waarde ervan te vinden. Trek 15 van beide kanten van de vergelijking af. 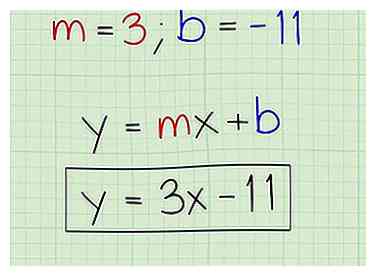 5 Schrijf de vergelijking van de middelloodlijn. Om de vergelijking van de middelloodlijn te schrijven, hoeft u alleen maar de helling van de lijn (3) en het y-snijpunt (-11) in te voegen in de vergelijking van een lijn in de vorm van hellingsonderbreking. U mag geen termen in de x- en y-coördinaten invoegen, omdat u met deze vergelijking elke coördinaat op de regel kunt vinden door een willekeurige x- of y-coördinaat in te voegen.
5 Schrijf de vergelijking van de middelloodlijn. Om de vergelijking van de middelloodlijn te schrijven, hoeft u alleen maar de helling van de lijn (3) en het y-snijpunt (-11) in te voegen in de vergelijking van een lijn in de vorm van hellingsonderbreking. U mag geen termen in de x- en y-coördinaten invoegen, omdat u met deze vergelijking elke coördinaat op de regel kunt vinden door een willekeurige x- of y-coördinaat in te voegen.