Een vector is een geometrisch object dat zowel een grootte als een richting heeft.[1] De grootte is de lengte van de vector, terwijl de richting de richting is. Het berekenen van de grootte van een vector is eenvoudig met een paar eenvoudige stappen. Andere belangrijke vectorbewerkingen omvatten het optellen en aftrekken van vectoren, het vinden van de hoek tussen twee vectoren en het vinden van het kruisproduct.
Methode één van de twee:
De grootte van een vector vinden bij de oorsprong
-
 1 Bepaal de componenten van de vector. Elke vector kan numeriek worden weergegeven in het cartesiaanse coördinatensysteem met een horizontale (x-as) en verticale (y-as) component.[2] Het is geschreven als een geordend paar .
1 Bepaal de componenten van de vector. Elke vector kan numeriek worden weergegeven in het cartesiaanse coördinatensysteem met een horizontale (x-as) en verticale (y-as) component.[2] Het is geschreven als een geordend paar . - De vector hierboven heeft bijvoorbeeld een horizontale component van 3 en een verticale component van -5, daarom is het geordende paar <3, -5>.
-
 2 Teken een vector driehoek. Wanneer u de horizontale en verticale componenten tekent, krijgt u een rechthoekige driehoek. De magnitude van de vector is gelijk aan de hypotenusa van de driehoek, dus je kunt de stelling van Pythagoras gebruiken om het te berekenen.
2 Teken een vector driehoek. Wanneer u de horizontale en verticale componenten tekent, krijgt u een rechthoekige driehoek. De magnitude van de vector is gelijk aan de hypotenusa van de driehoek, dus je kunt de stelling van Pythagoras gebruiken om het te berekenen. -
 3 Herschik de stelling van Pythagoras om de magnitude te berekenen. De stelling van Pythagoras is A2 + B2 = C2. "A" en "B" zijn de horizontale en verticale componenten van de driehoek, terwijl "C" de hypotenusa is. Omdat de vector de hypotenusa is die je wilt oplossen voor "C".
3 Herschik de stelling van Pythagoras om de magnitude te berekenen. De stelling van Pythagoras is A2 + B2 = C2. "A" en "B" zijn de horizontale en verticale componenten van de driehoek, terwijl "C" de hypotenusa is. Omdat de vector de hypotenusa is die je wilt oplossen voor "C". - X2 + y2 = v2
- v = √ (x2 + y2))
-
 4 Los op voor de magnitude. Met behulp van de bovenstaande vergelijking kunt u de nummers van het geordende paar van de vector aansluiten om de grootte op te lossen.
4 Los op voor de magnitude. Met behulp van de bovenstaande vergelijking kunt u de nummers van het geordende paar van de vector aansluiten om de grootte op te lossen. - Bijvoorbeeld, v = √ ((32+(-5)2))
- v = √ (9 + 25) = √34 = 5.831
- Maak je geen zorgen als je antwoord geen geheel getal is. Vectorgrootheden kunnen decimalen zijn.
Methode twee van twee:
De grootte van een vector vinden vanaf de oorsprong
-
 1 Bepaal de componenten van beide punten van de vector. Elke vector kan numeriek worden weergegeven in het cartesiaanse coördinatensysteem met een horizontale (x-as) en verticale (y-as) component.[3] Het is geschreven als een geordend paar . Als u een vector krijgt die is geplaatst weg van de oorsprong van het cartesiaanse coördinatensysteem, moet u de componenten van beide punten van de vector definiëren.
1 Bepaal de componenten van beide punten van de vector. Elke vector kan numeriek worden weergegeven in het cartesiaanse coördinatensysteem met een horizontale (x-as) en verticale (y-as) component.[3] Het is geschreven als een geordend paar . Als u een vector krijgt die is geplaatst weg van de oorsprong van het cartesiaanse coördinatensysteem, moet u de componenten van beide punten van de vector definiëren. - De vector AB heeft bijvoorbeeld een geordend paar voor punt A en punt B.
- Punt A heeft een horizontale component van 5 en een verticale component van 1, dus het geordende paar is <5, 1>.
- Punt B heeft een horizontale component van 1 en een verticale component van 2, dus het geordende paar is <1, 2>.
-
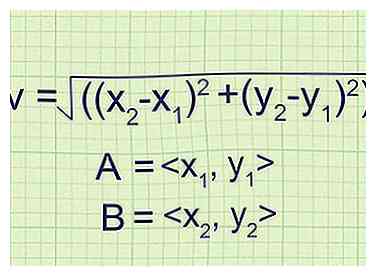 2 Gebruik een aangepaste formule om de grootte op te lossen. Omdat je nu twee punten hebt waar je mee te maken hebt, moet je de x- en y-componenten van elk punt aftrekken voordat je het oplost met behulp van de vergelijking v = √ ((x2-X1)2 + (Y2-y1)2).[4]
2 Gebruik een aangepaste formule om de grootte op te lossen. Omdat je nu twee punten hebt waar je mee te maken hebt, moet je de x- en y-componenten van elk punt aftrekken voordat je het oplost met behulp van de vergelijking v = √ ((x2-X1)2 + (Y2-y1)2).[4] - Punt A is geordend paar 1 <>1, y1> en punt B is paar 2 besteld <>2, y2>
-
 3 Los op voor de magnitude. Sluit de nummers van uw bestelde paren in en bereken de grootte. Met behulp van ons bovenstaande voorbeeld ziet de berekening er als volgt uit:
3 Los op voor de magnitude. Sluit de nummers van uw bestelde paren in en bereken de grootte. Met behulp van ons bovenstaande voorbeeld ziet de berekening er als volgt uit: - v = √ ((x2-X1)2 + (Y2-y1)2)
- v = √ ((1-5)2 +(2-1)2)
- v = √ ((- 4)2 +(1)2)
- v = √ (16 + 1) = √ (17) = 4.12
- Maak je geen zorgen als je antwoord geen geheel getal is. Vectorgrootheden kunnen decimalen zijn.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Bepaal de componenten van de vector. Elke vector kan numeriek worden weergegeven in het cartesiaanse coördinatensysteem met een horizontale (x-as) en verticale (y-as) component.[2] Het is geschreven als een geordend paar
1 Bepaal de componenten van de vector. Elke vector kan numeriek worden weergegeven in het cartesiaanse coördinatensysteem met een horizontale (x-as) en verticale (y-as) component.[2] Het is geschreven als een geordend paar  2 Teken een vector driehoek. Wanneer u de horizontale en verticale componenten tekent, krijgt u een rechthoekige driehoek. De magnitude van de vector is gelijk aan de hypotenusa van de driehoek, dus je kunt de stelling van Pythagoras gebruiken om het te berekenen.
2 Teken een vector driehoek. Wanneer u de horizontale en verticale componenten tekent, krijgt u een rechthoekige driehoek. De magnitude van de vector is gelijk aan de hypotenusa van de driehoek, dus je kunt de stelling van Pythagoras gebruiken om het te berekenen.  3 Herschik de stelling van Pythagoras om de magnitude te berekenen. De stelling van Pythagoras is A2 + B2 = C2. "A" en "B" zijn de horizontale en verticale componenten van de driehoek, terwijl "C" de hypotenusa is. Omdat de vector de hypotenusa is die je wilt oplossen voor "C".
3 Herschik de stelling van Pythagoras om de magnitude te berekenen. De stelling van Pythagoras is A2 + B2 = C2. "A" en "B" zijn de horizontale en verticale componenten van de driehoek, terwijl "C" de hypotenusa is. Omdat de vector de hypotenusa is die je wilt oplossen voor "C".  4 Los op voor de magnitude. Met behulp van de bovenstaande vergelijking kunt u de nummers van het geordende paar van de vector aansluiten om de grootte op te lossen.
4 Los op voor de magnitude. Met behulp van de bovenstaande vergelijking kunt u de nummers van het geordende paar van de vector aansluiten om de grootte op te lossen.  1 Bepaal de componenten van beide punten van de vector. Elke vector kan numeriek worden weergegeven in het cartesiaanse coördinatensysteem met een horizontale (x-as) en verticale (y-as) component.[3] Het is geschreven als een geordend paar
1 Bepaal de componenten van beide punten van de vector. Elke vector kan numeriek worden weergegeven in het cartesiaanse coördinatensysteem met een horizontale (x-as) en verticale (y-as) component.[3] Het is geschreven als een geordend paar 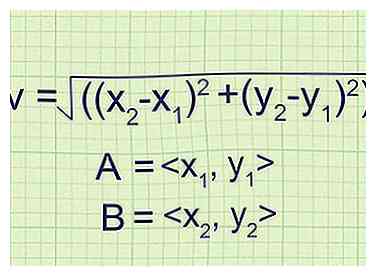 2 Gebruik een aangepaste formule om de grootte op te lossen. Omdat je nu twee punten hebt waar je mee te maken hebt, moet je de x- en y-componenten van elk punt aftrekken voordat je het oplost met behulp van de vergelijking v = √ ((x2-X1)2 + (Y2-y1)2).[4]
2 Gebruik een aangepaste formule om de grootte op te lossen. Omdat je nu twee punten hebt waar je mee te maken hebt, moet je de x- en y-componenten van elk punt aftrekken voordat je het oplost met behulp van de vergelijking v = √ ((x2-X1)2 + (Y2-y1)2).[4]  3 Los op voor de magnitude. Sluit de nummers van uw bestelde paren in en bereken de grootte. Met behulp van ons bovenstaande voorbeeld ziet de berekening er als volgt uit:
3 Los op voor de magnitude. Sluit de nummers van uw bestelde paren in en bereken de grootte. Met behulp van ons bovenstaande voorbeeld ziet de berekening er als volgt uit: