Asymptoten van een hyperbool zijn de lijnen die door het midden van de hyperbool lopen. De hyperbool komt steeds dichter bij de asymptoten, maar kan deze nooit bereiken. Er zijn twee verschillende benaderingen die u kunt gebruiken om de asymptoten te vinden. Door beide te leren, kun je het concept beter begrijpen.
Methode één van de twee:
factoring
-
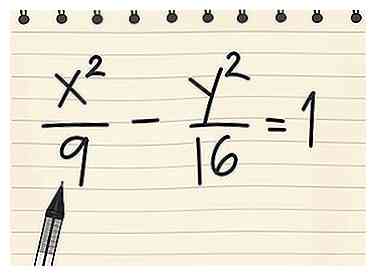 1 Noteer de vergelijking van de hyperbool in zijn standaardvorm. We beginnen met een eenvoudig voorbeeld: een hyperbool met het middelpunt van zijn oorsprong. Voor deze hyperbolas is de standaardvorm van de vergelijking X2/een2 - Y2/b2 = 1 voor hyperbolas die zich rechts en links uitstrekken, of Y2/b2 - X2/een2 = 1 voor hyperbolas die zich op en neer uitbreiden.[1] Onthoud dat x en y variabelen zijn, terwijl a en b constanten zijn (gewone getallen).
1 Noteer de vergelijking van de hyperbool in zijn standaardvorm. We beginnen met een eenvoudig voorbeeld: een hyperbool met het middelpunt van zijn oorsprong. Voor deze hyperbolas is de standaardvorm van de vergelijking X2/een2 - Y2/b2 = 1 voor hyperbolas die zich rechts en links uitstrekken, of Y2/b2 - X2/een2 = 1 voor hyperbolas die zich op en neer uitbreiden.[1] Onthoud dat x en y variabelen zijn, terwijl a en b constanten zijn (gewone getallen). - Voorbeeld 1: X2/9 - Y2/16 = 1
- Sommige schoolboeken en leerkrachten wisselen de positie van a en b in deze vergelijkingen.[2] Volg de vergelijking van dichtbij, zodat u begrijpt wat er aan de hand is. Als je de vergelijkingen gewoon onthoudt, ben je niet voorbereid als je een andere notatie ziet.
-
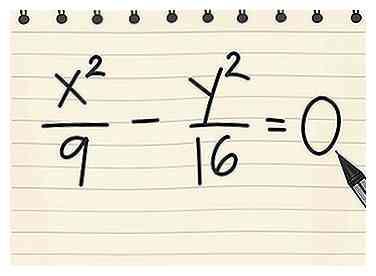 2 Stel de vergelijking gelijk aan nul in plaats van één. Deze nieuwe vergelijking vertegenwoordigt beide asymptoten, hoewel het iets meer moeite kost om ze van elkaar te scheiden.[3]
2 Stel de vergelijking gelijk aan nul in plaats van één. Deze nieuwe vergelijking vertegenwoordigt beide asymptoten, hoewel het iets meer moeite kost om ze van elkaar te scheiden.[3] - Voorbeeld 1: X2/9 - Y2/16 = 0
-
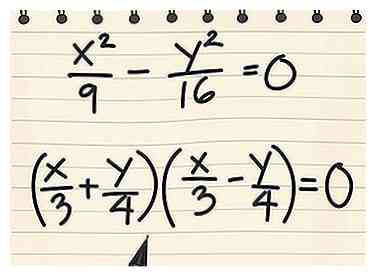 3 Factor de nieuwe vergelijking. Factor de linkerkant van de vergelijking in twee producten. Verfris je geheugen op het in rekening brengen van een kwadratische als dat nodig is, of volg het terwijl we doorgaan Voorbeeld 1:
3 Factor de nieuwe vergelijking. Factor de linkerkant van de vergelijking in twee producten. Verfris je geheugen op het in rekening brengen van een kwadratische als dat nodig is, of volg het terwijl we doorgaan Voorbeeld 1: - We zullen eindigen met een vergelijking in de vorm (__ ± __)(__ ± __) = 0.
- De eerste twee termen moeten samen vermenigvuldigen om te maken X2/9, dus neem de vierkantswortel en schrijf het in die spaties: (X/3 ± __)(X/3 ± __) = 0
- Neem op dezelfde manier de vierkantswortel van Y2/16 en plaats het in de twee resterende spaties: (X/3 ± Y/4)(X/3 ± Y/4) = 0
- Aangezien er geen andere voorwaarden zijn, schrijft u één plusteken en één minteken zodat de andere voorwaarden worden geannuleerd wanneer ze worden vermenigvuldigd: (X/3 + Y/4)(X/3 - Y/4) = 0
-
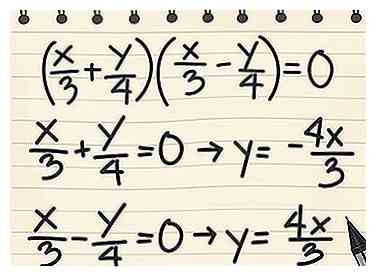 4 Scheid de factoren en los y op. Om de vergelijkingen voor de asymptoten te krijgen, scheidt u de twee factoren en lost u op in termen van y.
4 Scheid de factoren en los y op. Om de vergelijkingen voor de asymptoten te krijgen, scheidt u de twee factoren en lost u op in termen van y. - Voorbeeld 1: Sinds (X/3 + Y/4)(X/3 - Y/4) = 0, wij weten X/3 + Y/4 = 0 en X/3 - Y/4 = 0
- Herschrijven X/3 + Y/4 = 0 → Y/4 = - X/3 → y = - 4x/3
- Herschrijven X/3 - Y/4 = 0 → - Y/4 = - X/3 → y = 4x/3
-
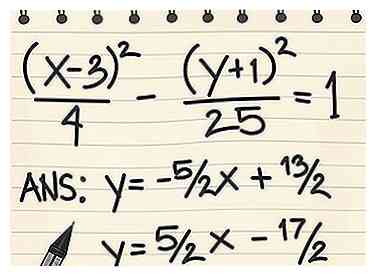 5 Probeer hetzelfde proces met een moeilijkere vergelijking. We hebben zojuist de asymptoten gevonden voor een hyperbool met als middelpunt de oorsprong. Een hyperbool gecentreerd op (h, k) heeft een vergelijking in de vorm (x - h)2/een2 - (y - k)2/b2 = 1of in de vorm (y - k)2/b2 - (x - h)2/een2 = 1. U kunt deze oplossen met exact dezelfde factoringmethode die hierboven is beschreven. Laat de (x - h) en (y - k) termen intact tot de laatste stap.
5 Probeer hetzelfde proces met een moeilijkere vergelijking. We hebben zojuist de asymptoten gevonden voor een hyperbool met als middelpunt de oorsprong. Een hyperbool gecentreerd op (h, k) heeft een vergelijking in de vorm (x - h)2/een2 - (y - k)2/b2 = 1of in de vorm (y - k)2/b2 - (x - h)2/een2 = 1. U kunt deze oplossen met exact dezelfde factoringmethode die hierboven is beschreven. Laat de (x - h) en (y - k) termen intact tot de laatste stap. - Voorbeeld 2: (x - 3)2/4 - (y + 1)2/25 = 1
- Stel dit gelijk aan 0 en factor om te krijgen:
- ((x - 3)/2 + (y + 1)/5)((x - 3)/2 - (y + 1)/5) = 0
- Scheid elke factor en los op om de vergelijkingen van de asymptoten te vinden:
- (x - 3)/2 + (y + 1)/5 = 0 → y = -5/2x + 13/2
- ((x - 3)/2 - (y + 1)/5) = 0 → y = 5/2x - 17/2
Methode twee van twee:
Oplossen voor Y
-
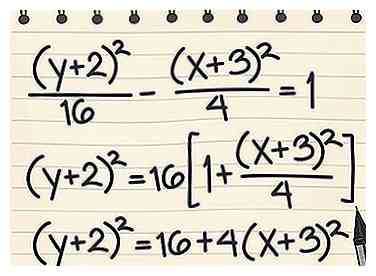 1 Noteer de hyperboolvergelijking met de y2 termijn aan de linkerkant. Deze methode is handig als u een vergelijking in algemene kwadratische vorm heeft. Zelfs als het in standaardvorm is voor hyperbolen, kan deze benadering u enig inzicht geven in de aard van asymptoten. Herschik de vergelijking zo dat de y2 of (y - k)2 termijn is aan de ene kant om te beginnen.
1 Noteer de hyperboolvergelijking met de y2 termijn aan de linkerkant. Deze methode is handig als u een vergelijking in algemene kwadratische vorm heeft. Zelfs als het in standaardvorm is voor hyperbolen, kan deze benadering u enig inzicht geven in de aard van asymptoten. Herschik de vergelijking zo dat de y2 of (y - k)2 termijn is aan de ene kant om te beginnen. - Voorbeeld 3: (y + 2)2/16 - (x + 3)2/4 = 1
- Voeg de x-term toe aan beide zijden en vermenigvuldig elke kant met 16:
- (y + 2)2 = 16(1 + (x + 3)2/4)
- Makkelijker maken:
- (y + 2)2 = 16 + 4 (x + 3)2
-
 2 Neem de vierkantswortel van elke kant. Neem de vierkantswortel, maar probeer de rechterkant nog niet te vereenvoudigen. Onthoud dat wanneer u de vierkantswortel neemt, er twee mogelijke oplossingen zijn: een positieve en een negatieve. (Bijvoorbeeld -2 * -2 = 4, dus √4 kan gelijk zijn aan -2 evenals 2.) Gebruik het "+ or -" teken ± om beide oplossingen bij te houden.
2 Neem de vierkantswortel van elke kant. Neem de vierkantswortel, maar probeer de rechterkant nog niet te vereenvoudigen. Onthoud dat wanneer u de vierkantswortel neemt, er twee mogelijke oplossingen zijn: een positieve en een negatieve. (Bijvoorbeeld -2 * -2 = 4, dus √4 kan gelijk zijn aan -2 evenals 2.) Gebruik het "+ or -" teken ± om beide oplossingen bij te houden. - √ ((y + 2)2) = √ (16 + 4 (x + 3)2)
- (y + 2) = ± √ (16 + 4 (x + 3)2)
-
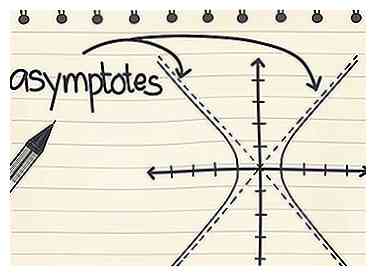 3 Bekijk de definitie van een asymptoot. Het is belangrijk dat u dit begrijpt voordat u doorgaat naar de volgende stap. De asymptoot van een hyperbool is een lijn die de hyperbool steeds dichter nadert naarmate x toeneemt. X kan de asymptoot nooit bereiken, maar als we de hyperbool volgen voor grotere en grotere waarden van x, komen we steeds dichter bij de asymptoot.
3 Bekijk de definitie van een asymptoot. Het is belangrijk dat u dit begrijpt voordat u doorgaat naar de volgende stap. De asymptoot van een hyperbool is een lijn die de hyperbool steeds dichter nadert naarmate x toeneemt. X kan de asymptoot nooit bereiken, maar als we de hyperbool volgen voor grotere en grotere waarden van x, komen we steeds dichter bij de asymptoot. -
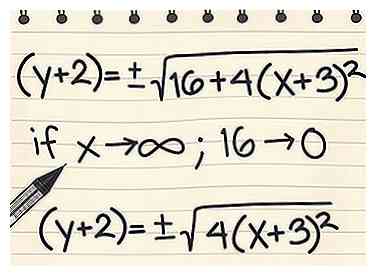 4 Pas de vergelijking aan voor grote waarden van x. Omdat we nu de asymptote-vergelijking proberen te vinden, geven we alleen om x voor zeer grote waarden ("het naderende oneindige"). Dit laat ons bepaalde constanten in de vergelijking negeren, omdat ze zo'n klein deel bijdragen ten opzichte van de x-term. Zodra x op 99 miljard is (bijvoorbeeld), is het toevoegen van drie zo klein dat we het kunnen negeren.
4 Pas de vergelijking aan voor grote waarden van x. Omdat we nu de asymptote-vergelijking proberen te vinden, geven we alleen om x voor zeer grote waarden ("het naderende oneindige"). Dit laat ons bepaalde constanten in de vergelijking negeren, omdat ze zo'n klein deel bijdragen ten opzichte van de x-term. Zodra x op 99 miljard is (bijvoorbeeld), is het toevoegen van drie zo klein dat we het kunnen negeren. - In de vergelijking (y + 2) = ± √ (16 + 4 (x + 3)2), als x het oneindige nadert, wordt de 16 irrelevant.
- (y + 2) = ongeveer ± √ (4 (x + 3)2) voor grote waarden van x
-
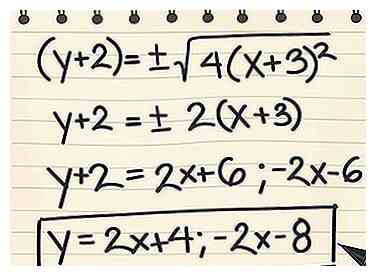 5 Los op voor y om de twee asymptootvergelijkingen te vinden. Nu we van de constante af zijn, kunnen we de vierkantswortel vereenvoudigen. Los op in termen van y om het antwoord te krijgen. Vergeet niet om het symbool ± te splitsen in twee afzonderlijke vergelijkingen, één met + en één met -.
5 Los op voor y om de twee asymptootvergelijkingen te vinden. Nu we van de constante af zijn, kunnen we de vierkantswortel vereenvoudigen. Los op in termen van y om het antwoord te krijgen. Vergeet niet om het symbool ± te splitsen in twee afzonderlijke vergelijkingen, één met + en één met -. - y + 2 = ± √ (4 (x + 3) ^ 2)
- y + 2 = ± 2 (x + 3)
- y + 2 = 2x + 6 en y + 2 = -2x - 6
- y = 2x + 4 en y = -2x - 8
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
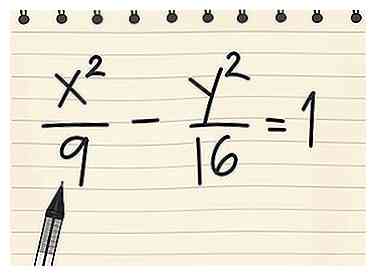 1 Noteer de vergelijking van de hyperbool in zijn standaardvorm. We beginnen met een eenvoudig voorbeeld: een hyperbool met het middelpunt van zijn oorsprong. Voor deze hyperbolas is de standaardvorm van de vergelijking X2/een2 - Y2/b2 = 1 voor hyperbolas die zich rechts en links uitstrekken, of Y2/b2 - X2/een2 = 1 voor hyperbolas die zich op en neer uitbreiden.[1] Onthoud dat x en y variabelen zijn, terwijl a en b constanten zijn (gewone getallen).
1 Noteer de vergelijking van de hyperbool in zijn standaardvorm. We beginnen met een eenvoudig voorbeeld: een hyperbool met het middelpunt van zijn oorsprong. Voor deze hyperbolas is de standaardvorm van de vergelijking X2/een2 - Y2/b2 = 1 voor hyperbolas die zich rechts en links uitstrekken, of Y2/b2 - X2/een2 = 1 voor hyperbolas die zich op en neer uitbreiden.[1] Onthoud dat x en y variabelen zijn, terwijl a en b constanten zijn (gewone getallen). 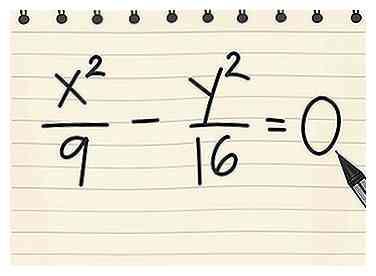 2 Stel de vergelijking gelijk aan nul in plaats van één. Deze nieuwe vergelijking vertegenwoordigt beide asymptoten, hoewel het iets meer moeite kost om ze van elkaar te scheiden.[3]
2 Stel de vergelijking gelijk aan nul in plaats van één. Deze nieuwe vergelijking vertegenwoordigt beide asymptoten, hoewel het iets meer moeite kost om ze van elkaar te scheiden.[3] 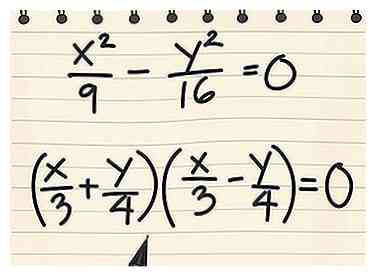 3 Factor de nieuwe vergelijking. Factor de linkerkant van de vergelijking in twee producten. Verfris je geheugen op het in rekening brengen van een kwadratische als dat nodig is, of volg het terwijl we doorgaan Voorbeeld 1:
3 Factor de nieuwe vergelijking. Factor de linkerkant van de vergelijking in twee producten. Verfris je geheugen op het in rekening brengen van een kwadratische als dat nodig is, of volg het terwijl we doorgaan Voorbeeld 1: 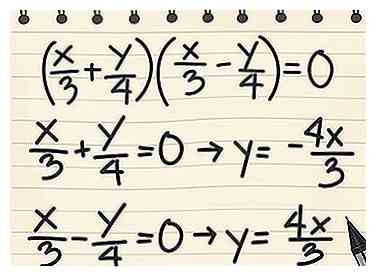 4 Scheid de factoren en los y op. Om de vergelijkingen voor de asymptoten te krijgen, scheidt u de twee factoren en lost u op in termen van y.
4 Scheid de factoren en los y op. Om de vergelijkingen voor de asymptoten te krijgen, scheidt u de twee factoren en lost u op in termen van y. 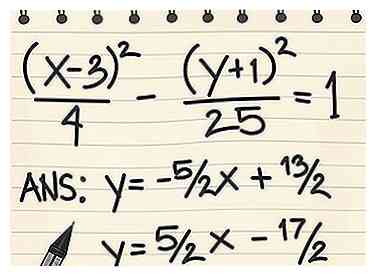 5 Probeer hetzelfde proces met een moeilijkere vergelijking. We hebben zojuist de asymptoten gevonden voor een hyperbool met als middelpunt de oorsprong. Een hyperbool gecentreerd op (h, k) heeft een vergelijking in de vorm (x - h)2/een2 - (y - k)2/b2 = 1of in de vorm (y - k)2/b2 - (x - h)2/een2 = 1. U kunt deze oplossen met exact dezelfde factoringmethode die hierboven is beschreven. Laat de (x - h) en (y - k) termen intact tot de laatste stap.
5 Probeer hetzelfde proces met een moeilijkere vergelijking. We hebben zojuist de asymptoten gevonden voor een hyperbool met als middelpunt de oorsprong. Een hyperbool gecentreerd op (h, k) heeft een vergelijking in de vorm (x - h)2/een2 - (y - k)2/b2 = 1of in de vorm (y - k)2/b2 - (x - h)2/een2 = 1. U kunt deze oplossen met exact dezelfde factoringmethode die hierboven is beschreven. Laat de (x - h) en (y - k) termen intact tot de laatste stap. 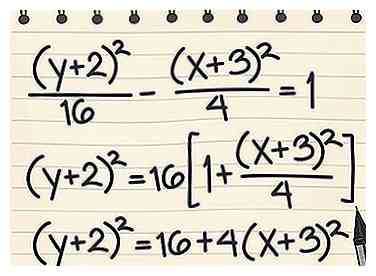 1 Noteer de hyperboolvergelijking met de y2 termijn aan de linkerkant. Deze methode is handig als u een vergelijking in algemene kwadratische vorm heeft. Zelfs als het in standaardvorm is voor hyperbolen, kan deze benadering u enig inzicht geven in de aard van asymptoten. Herschik de vergelijking zo dat de y2 of (y - k)2 termijn is aan de ene kant om te beginnen.
1 Noteer de hyperboolvergelijking met de y2 termijn aan de linkerkant. Deze methode is handig als u een vergelijking in algemene kwadratische vorm heeft. Zelfs als het in standaardvorm is voor hyperbolen, kan deze benadering u enig inzicht geven in de aard van asymptoten. Herschik de vergelijking zo dat de y2 of (y - k)2 termijn is aan de ene kant om te beginnen.  2 Neem de vierkantswortel van elke kant. Neem de vierkantswortel, maar probeer de rechterkant nog niet te vereenvoudigen. Onthoud dat wanneer u de vierkantswortel neemt, er twee mogelijke oplossingen zijn: een positieve en een negatieve. (Bijvoorbeeld -2 * -2 = 4, dus √4 kan gelijk zijn aan -2 evenals 2.) Gebruik het "+ or -" teken ± om beide oplossingen bij te houden.
2 Neem de vierkantswortel van elke kant. Neem de vierkantswortel, maar probeer de rechterkant nog niet te vereenvoudigen. Onthoud dat wanneer u de vierkantswortel neemt, er twee mogelijke oplossingen zijn: een positieve en een negatieve. (Bijvoorbeeld -2 * -2 = 4, dus √4 kan gelijk zijn aan -2 evenals 2.) Gebruik het "+ or -" teken ± om beide oplossingen bij te houden.  3 Bekijk de definitie van een asymptoot. Het is belangrijk dat u dit begrijpt voordat u doorgaat naar de volgende stap. De asymptoot van een hyperbool is een lijn die de hyperbool steeds dichter nadert naarmate x toeneemt. X kan de asymptoot nooit bereiken, maar als we de hyperbool volgen voor grotere en grotere waarden van x, komen we steeds dichter bij de asymptoot.
3 Bekijk de definitie van een asymptoot. Het is belangrijk dat u dit begrijpt voordat u doorgaat naar de volgende stap. De asymptoot van een hyperbool is een lijn die de hyperbool steeds dichter nadert naarmate x toeneemt. X kan de asymptoot nooit bereiken, maar als we de hyperbool volgen voor grotere en grotere waarden van x, komen we steeds dichter bij de asymptoot. 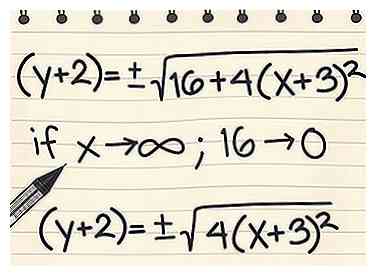 4 Pas de vergelijking aan voor grote waarden van x. Omdat we nu de asymptote-vergelijking proberen te vinden, geven we alleen om x voor zeer grote waarden ("het naderende oneindige"). Dit laat ons bepaalde constanten in de vergelijking negeren, omdat ze zo'n klein deel bijdragen ten opzichte van de x-term. Zodra x op 99 miljard is (bijvoorbeeld), is het toevoegen van drie zo klein dat we het kunnen negeren.
4 Pas de vergelijking aan voor grote waarden van x. Omdat we nu de asymptote-vergelijking proberen te vinden, geven we alleen om x voor zeer grote waarden ("het naderende oneindige"). Dit laat ons bepaalde constanten in de vergelijking negeren, omdat ze zo'n klein deel bijdragen ten opzichte van de x-term. Zodra x op 99 miljard is (bijvoorbeeld), is het toevoegen van drie zo klein dat we het kunnen negeren. 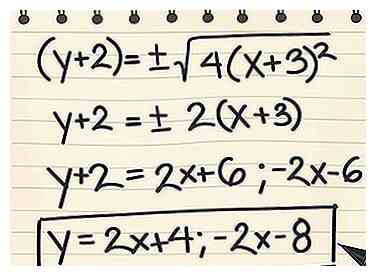 5 Los op voor y om de twee asymptootvergelijkingen te vinden. Nu we van de constante af zijn, kunnen we de vierkantswortel vereenvoudigen. Los op in termen van y om het antwoord te krijgen. Vergeet niet om het symbool ± te splitsen in twee afzonderlijke vergelijkingen, één met + en één met -.
5 Los op voor y om de twee asymptootvergelijkingen te vinden. Nu we van de constante af zijn, kunnen we de vierkantswortel vereenvoudigen. Los op in termen van y om het antwoord te krijgen. Vergeet niet om het symbool ± te splitsen in twee afzonderlijke vergelijkingen, één met + en één met -.