In de wiskunde is een vector een object met een definieerbare lengte, die bekend staat als magnitude en richting. Omdat vectoren niet hetzelfde zijn als standaardlijnen of vormen, moet u een aantal speciale formules gebruiken om hoeken tussen beide te vinden.
Deel een van de twee:
De hoek tussen twee vectoren vinden
-
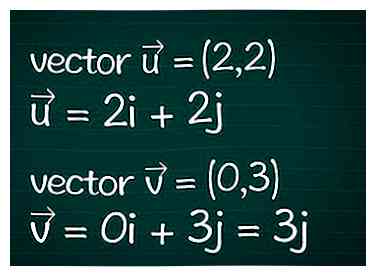 1 Identificeer de vectoren. Noteer alle informatie die u heeft over de twee vectoren. We gaan ervan uit dat je alleen de definitie van de vector hebt in termen van zijn dimensionale coördinaten (ook wel componenten genoemd). Als u de lengte van een vector al kent (zijn magnitude), kunt u enkele van de onderstaande stappen overslaan.
1 Identificeer de vectoren. Noteer alle informatie die u heeft over de twee vectoren. We gaan ervan uit dat je alleen de definitie van de vector hebt in termen van zijn dimensionale coördinaten (ook wel componenten genoemd). Als u de lengte van een vector al kent (zijn magnitude), kunt u enkele van de onderstaande stappen overslaan. - Voorbeeld: de tweedimensionale vector = (2,2). Vector = (0,3). Deze kunnen ook als worden geschreven = 2ik + 2j en = 0ik + 3j = 3j.
- Hoewel ons voorbeeld tweedimensionale vectoren gebruikt, behandelen de onderstaande instructies vectoren met een willekeurig aantal componenten.
-
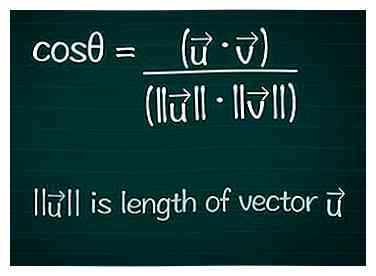 2 Noteer de cosinus-formule. Om de hoek θ tussen twee vectoren te vinden, begint u met de formule om de cosinus van die hoek te vinden. U kunt hieronder meer informatie over deze formule krijgen of gewoon opschrijven:[1]
2 Noteer de cosinus-formule. Om de hoek θ tussen twee vectoren te vinden, begint u met de formule om de cosinus van die hoek te vinden. U kunt hieronder meer informatie over deze formule krijgen of gewoon opschrijven:[1] - cosθ = ( • ) / (|||| ||||)
- |||| betekent "de lengte van de vector ."
- • is het puntproduct (scalair product) van de twee vectoren, hieronder uitgelegd.
-
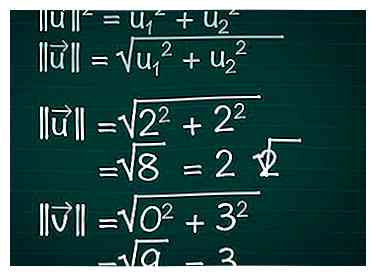 3 Bereken de lengte van elke vector. Stel een rechthoekige driehoek voor die wordt getekend door de x-component van de vector, de y-component ervan en de vector zelf. De vector vormt de hypotenusa van de driehoek, dus om de lengte te vinden gebruiken we de stelling van Pythagoras. Het blijkt dat deze formule eenvoudig kan worden uitgebreid naar vectoren met een willekeurig aantal componenten.
3 Bereken de lengte van elke vector. Stel een rechthoekige driehoek voor die wordt getekend door de x-component van de vector, de y-component ervan en de vector zelf. De vector vormt de hypotenusa van de driehoek, dus om de lengte te vinden gebruiken we de stelling van Pythagoras. Het blijkt dat deze formule eenvoudig kan worden uitgebreid naar vectoren met een willekeurig aantal componenten.
Vectorlengtevoorbeeld berekenen
||u||2 = u12 + u22. Als een vector meer dan twee componenten heeft, gaat u gewoon door met het toevoegen van + u32 + u42 +…
Daarom voor een tweedimensionale vector, ||u|| = √ (u12 + u22).
In ons voorbeeld |||| = √(22 + 22) = √(8) = 2√2. |||| = √(02 + 32) = √(9) = 3.
-
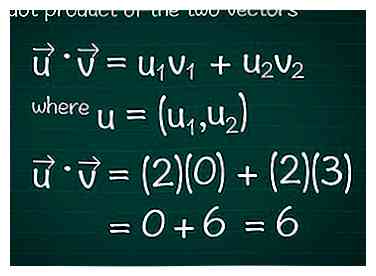 4 Bereken het puntproduct van de twee vectoren. Je hebt deze methode van vermenigvuldigen van vectoren waarschijnlijk al geleerd, ook wel de scalair product.[2]Als u het puntproduct wilt berekenen in termen van de componenten van de vectoren, vermenigvuldigt u de componenten in elke richting samen en voegt u vervolgens alle resultaten toe. Zie Tips voor computer grafische programma's voordat u doorgaat. Dot Product Voorbeeld vinden
4 Bereken het puntproduct van de twee vectoren. Je hebt deze methode van vermenigvuldigen van vectoren waarschijnlijk al geleerd, ook wel de scalair product.[2]Als u het puntproduct wilt berekenen in termen van de componenten van de vectoren, vermenigvuldigt u de componenten in elke richting samen en voegt u vervolgens alle resultaten toe. Zie Tips voor computer grafische programma's voordat u doorgaat. Dot Product Voorbeeld vinden
In wiskundige termen, • = u1v1 + u2v2, waar u = (u1, jij2). Als uw vector meer dan twee componenten heeft, blijft u + u toevoegen3v3 + u4v4…
In ons voorbeeld • = u1v1 + u2v2 = (2)(0) + (2)(3) = 0 + 6 = 6. Dit is het puntproduct van vector en .
-
 5 Sluit uw resultaten aan in de formule. Onthoud, cosθ = ( • ) / (|||| || ||). Nu kent u zowel het puntproduct als de lengte van elke vector. Voer deze in deze formule in om de cosinus van de hoek te berekenen. Cosinus vinden met puntproduct en vectorlengten
5 Sluit uw resultaten aan in de formule. Onthoud, cosθ = ( • ) / (|||| || ||). Nu kent u zowel het puntproduct als de lengte van elke vector. Voer deze in deze formule in om de cosinus van de hoek te berekenen. Cosinus vinden met puntproduct en vectorlengten
In ons voorbeeld is cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.
-
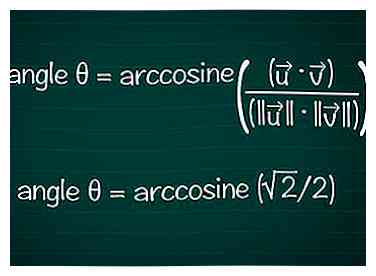 6 Zoek de hoek op basis van de cosinus. U kunt de arccos of cos-1 functie op uw rekenmachine om de hoek θ te vinden van een bekende cos θ waarde. Voor sommige resultaten kunt u mogelijk de hoek berekenen op basis van de eenheidscirkel. Een hoek vinden met Cosine
6 Zoek de hoek op basis van de cosinus. U kunt de arccos of cos-1 functie op uw rekenmachine om de hoek θ te vinden van een bekende cos θ waarde. Voor sommige resultaten kunt u mogelijk de hoek berekenen op basis van de eenheidscirkel. Een hoek vinden met Cosine
In ons voorbeeld cosθ = √2 / 2. Voer "arccos (√2 / 2)" in uw rekenmachine in om de hoek te krijgen. Zoek anders de hoek θ op de eenheidscirkel waar cosθ = √2 / 2. Dit is waar voor θ = π/4 of 45º.
Alles bij elkaar is de uiteindelijke formule: hoek θ = arccosine (( • ) / (|||| || ||))
Deel twee van twee:
De hoekformule definiëren
-
 1 Begrijp het doel van deze formule. Deze formule is niet afgeleid van bestaande regels. In plaats daarvan is het gemaakt als een definitie van het puntproduct van twee vectoren en de hoek ertussen.[3] Deze beslissing was echter niet willekeurig.Met een terugblik op de basisgeometrie, kunnen we zien waarom deze formule resulteert in intuïtieve en bruikbare definities.
1 Begrijp het doel van deze formule. Deze formule is niet afgeleid van bestaande regels. In plaats daarvan is het gemaakt als een definitie van het puntproduct van twee vectoren en de hoek ertussen.[3] Deze beslissing was echter niet willekeurig.Met een terugblik op de basisgeometrie, kunnen we zien waarom deze formule resulteert in intuïtieve en bruikbare definities. - De onderstaande voorbeelden gebruiken tweedimensionale vectoren omdat deze het meest intuïtief zijn om te gebruiken. Vectoren met drie of meer componenten hebben eigenschappen die zijn gedefinieerd met de zeer vergelijkbare, algemene casusformule.
-
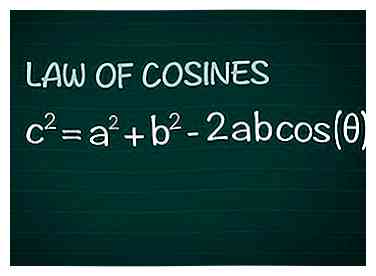 2 Herzie de wet van Cosinus. Neem een gewone driehoek, met hoek θ tussen zijden a en b, en tegenoverliggende kant c. De wet van Cosinus stelt dat c2 = a2 + b2 -2abcos(Θ). Dit wordt vrij gemakkelijk afgeleid van de basisgeometrie.
2 Herzie de wet van Cosinus. Neem een gewone driehoek, met hoek θ tussen zijden a en b, en tegenoverliggende kant c. De wet van Cosinus stelt dat c2 = a2 + b2 -2abcos(Θ). Dit wordt vrij gemakkelijk afgeleid van de basisgeometrie. -
 3 Verbind twee vectoren om een driehoek te vormen. Schets een paar 2D-vectoren op papier, vectoren en , met een hoek θ ertussen. Trek een derde vector ertussen om een driehoek te maken. Met andere woorden, teken vector zoals dat + = . Deze vector = - .[4]
3 Verbind twee vectoren om een driehoek te vormen. Schets een paar 2D-vectoren op papier, vectoren en , met een hoek θ ertussen. Trek een derde vector ertussen om een driehoek te maken. Met andere woorden, teken vector zoals dat + = . Deze vector = - .[4] -
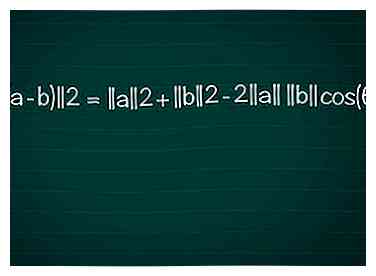 4 Schrijf de wet van cosinus voor deze driehoek. Plaats de lengte van onze "vector driehoek" zijden in de Wet van Cosinus:
4 Schrijf de wet van cosinus voor deze driehoek. Plaats de lengte van onze "vector driehoek" zijden in de Wet van Cosinus: - ||(a - b)||2 = ||een||2 + ||b||2 - 2||een|| ||b||cos(θ)
-
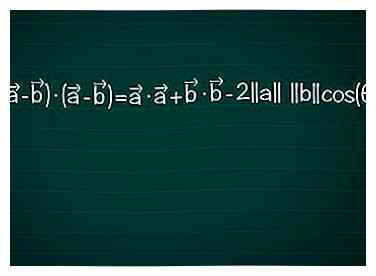 5 Schrijf dit met behulp van puntproducten. Vergeet niet dat een puntproduct de vergroting is van de ene vector die op de andere wordt geprojecteerd. Een puntproduct van een vector met zichzelf vereist geen projectie, omdat er geen verschil in richting is.[5] Dit betekent dat • = ||een||2. Gebruik dit feit om de vergelijking te herschrijven:
5 Schrijf dit met behulp van puntproducten. Vergeet niet dat een puntproduct de vergroting is van de ene vector die op de andere wordt geprojecteerd. Een puntproduct van een vector met zichzelf vereist geen projectie, omdat er geen verschil in richting is.[5] Dit betekent dat • = ||een||2. Gebruik dit feit om de vergelijking te herschrijven: - ( - ) • ( - ) = • + • - 2||een|| ||b||cos(θ)
-
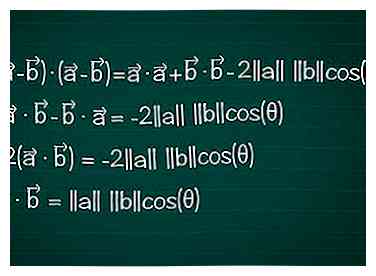 6 Herschrijf het in de vertrouwde formule. Vouw de linkerkant van de formule uit en vereenvoudig om de formule te gebruiken die wordt gebruikt om hoeken te vinden.
6 Herschrijf het in de vertrouwde formule. Vouw de linkerkant van de formule uit en vereenvoudig om de formule te gebruiken die wordt gebruikt om hoeken te vinden. - • - • - • + • = • + • - 2||een|| ||b||cos(θ)
- - • - • = -2||een|| ||b||cos(θ)
- -2( • ) = -2||een|| ||b||cos(θ)
- • = ||een|| ||b||cos(θ)
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
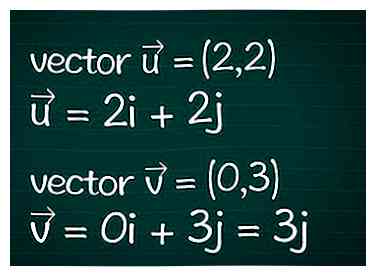 1 Identificeer de vectoren. Noteer alle informatie die u heeft over de twee vectoren. We gaan ervan uit dat je alleen de definitie van de vector hebt in termen van zijn dimensionale coördinaten (ook wel componenten genoemd). Als u de lengte van een vector al kent (zijn magnitude), kunt u enkele van de onderstaande stappen overslaan.
1 Identificeer de vectoren. Noteer alle informatie die u heeft over de twee vectoren. We gaan ervan uit dat je alleen de definitie van de vector hebt in termen van zijn dimensionale coördinaten (ook wel componenten genoemd). Als u de lengte van een vector al kent (zijn magnitude), kunt u enkele van de onderstaande stappen overslaan. 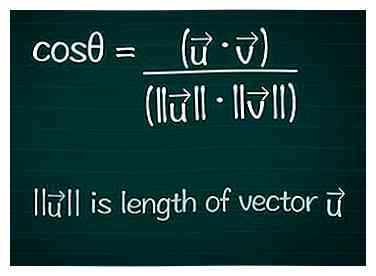 2 Noteer de cosinus-formule. Om de hoek θ tussen twee vectoren te vinden, begint u met de formule om de cosinus van die hoek te vinden. U kunt hieronder meer informatie over deze formule krijgen of gewoon opschrijven:[1]
2 Noteer de cosinus-formule. Om de hoek θ tussen twee vectoren te vinden, begint u met de formule om de cosinus van die hoek te vinden. U kunt hieronder meer informatie over deze formule krijgen of gewoon opschrijven:[1] 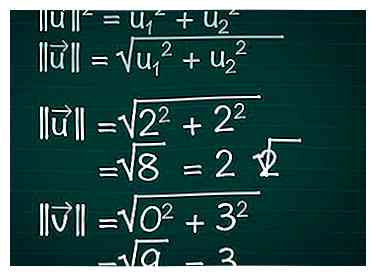 3 Bereken de lengte van elke vector. Stel een rechthoekige driehoek voor die wordt getekend door de x-component van de vector, de y-component ervan en de vector zelf. De vector vormt de hypotenusa van de driehoek, dus om de lengte te vinden gebruiken we de stelling van Pythagoras. Het blijkt dat deze formule eenvoudig kan worden uitgebreid naar vectoren met een willekeurig aantal componenten.
3 Bereken de lengte van elke vector. Stel een rechthoekige driehoek voor die wordt getekend door de x-component van de vector, de y-component ervan en de vector zelf. De vector vormt de hypotenusa van de driehoek, dus om de lengte te vinden gebruiken we de stelling van Pythagoras. Het blijkt dat deze formule eenvoudig kan worden uitgebreid naar vectoren met een willekeurig aantal componenten.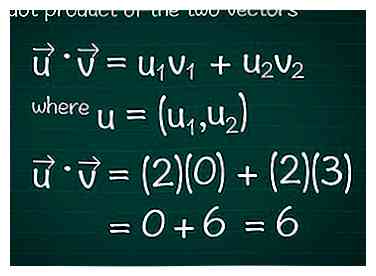 4 Bereken het puntproduct van de twee vectoren. Je hebt deze methode van vermenigvuldigen van vectoren waarschijnlijk al geleerd, ook wel de scalair product.[2]Als u het puntproduct wilt berekenen in termen van de componenten van de vectoren, vermenigvuldigt u de componenten in elke richting samen en voegt u vervolgens alle resultaten toe. Zie Tips voor computer grafische programma's voordat u doorgaat.
4 Bereken het puntproduct van de twee vectoren. Je hebt deze methode van vermenigvuldigen van vectoren waarschijnlijk al geleerd, ook wel de scalair product.[2]Als u het puntproduct wilt berekenen in termen van de componenten van de vectoren, vermenigvuldigt u de componenten in elke richting samen en voegt u vervolgens alle resultaten toe. Zie Tips voor computer grafische programma's voordat u doorgaat.  5 Sluit uw resultaten aan in de formule. Onthoud, cosθ = (
5 Sluit uw resultaten aan in de formule. Onthoud, cosθ = (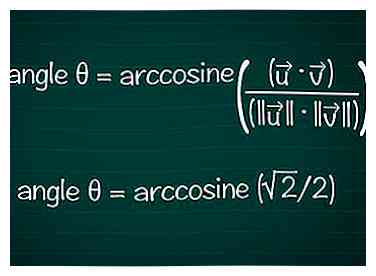 6 Zoek de hoek op basis van de cosinus. U kunt de
6 Zoek de hoek op basis van de cosinus. U kunt de  1 Begrijp het doel van deze formule. Deze formule is niet afgeleid van bestaande regels. In plaats daarvan is het gemaakt als een definitie van het puntproduct van twee vectoren en de hoek ertussen.[3] Deze beslissing was echter niet willekeurig.Met een terugblik op de basisgeometrie, kunnen we zien waarom deze formule resulteert in intuïtieve en bruikbare definities.
1 Begrijp het doel van deze formule. Deze formule is niet afgeleid van bestaande regels. In plaats daarvan is het gemaakt als een definitie van het puntproduct van twee vectoren en de hoek ertussen.[3] Deze beslissing was echter niet willekeurig.Met een terugblik op de basisgeometrie, kunnen we zien waarom deze formule resulteert in intuïtieve en bruikbare definities. 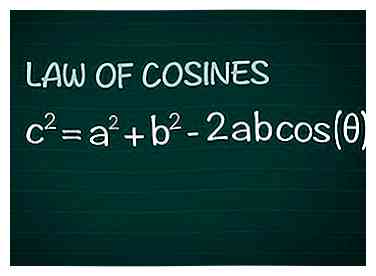 2 Herzie de wet van Cosinus. Neem een gewone driehoek, met hoek θ tussen zijden a en b, en tegenoverliggende kant c. De wet van Cosinus stelt dat c2 = a2 + b2 -2abcos(Θ). Dit wordt vrij gemakkelijk afgeleid van de basisgeometrie.
2 Herzie de wet van Cosinus. Neem een gewone driehoek, met hoek θ tussen zijden a en b, en tegenoverliggende kant c. De wet van Cosinus stelt dat c2 = a2 + b2 -2abcos(Θ). Dit wordt vrij gemakkelijk afgeleid van de basisgeometrie.  3 Verbind twee vectoren om een driehoek te vormen. Schets een paar 2D-vectoren op papier, vectoren
3 Verbind twee vectoren om een driehoek te vormen. Schets een paar 2D-vectoren op papier, vectoren 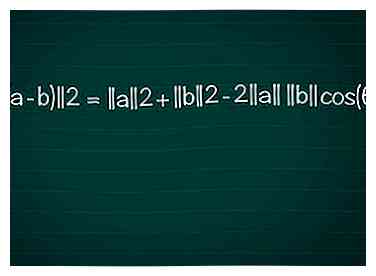 4 Schrijf de wet van cosinus voor deze driehoek. Plaats de lengte van onze "vector driehoek" zijden in de Wet van Cosinus:
4 Schrijf de wet van cosinus voor deze driehoek. Plaats de lengte van onze "vector driehoek" zijden in de Wet van Cosinus: 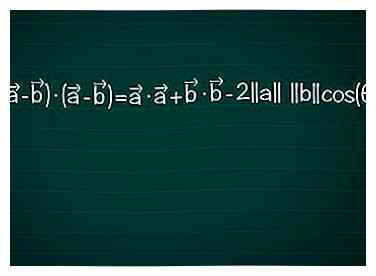 5 Schrijf dit met behulp van puntproducten. Vergeet niet dat een puntproduct de vergroting is van de ene vector die op de andere wordt geprojecteerd. Een puntproduct van een vector met zichzelf vereist geen projectie, omdat er geen verschil in richting is.[5] Dit betekent dat
5 Schrijf dit met behulp van puntproducten. Vergeet niet dat een puntproduct de vergroting is van de ene vector die op de andere wordt geprojecteerd. Een puntproduct van een vector met zichzelf vereist geen projectie, omdat er geen verschil in richting is.[5] Dit betekent dat 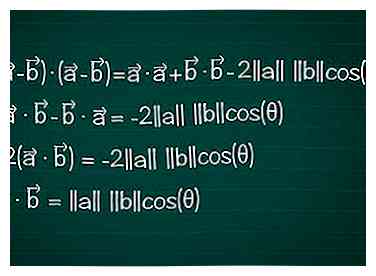 6 Herschrijf het in de vertrouwde formule. Vouw de linkerkant van de formule uit en vereenvoudig om de formule te gebruiken die wordt gebruikt om hoeken te vinden.
6 Herschrijf het in de vertrouwde formule. Vouw de linkerkant van de formule uit en vereenvoudig om de formule te gebruiken die wordt gebruikt om hoeken te vinden.