Grafieken van vergelijkingen is een veel eenvoudiger proces dat de meeste mensen zich realiseren. Je hoeft geen wiskundig genie of een straight-A student te zijn om de basisprincipes van het tekenen te leren zonder een rekenmachine te gebruiken. Leer enkele van deze methoden voor het tekenen van lineaire, kwadratische, ongelijke en absolute waardevergelijkingen.
Methode één van de zes:
Grafische lineaire vergelijkingen
-
 1 Gebruik de formule y = mx + b. Als u een lineaire vergelijking wilt tekenen, moet u alleen de variabelen in deze formule vervangen.
1 Gebruik de formule y = mx + b. Als u een lineaire vergelijking wilt tekenen, moet u alleen de variabelen in deze formule vervangen. - In de formule lost u op voor (x, y).
- De variabele m = helling. De helling wordt ook genoteerd als stijging boven de vlucht, of het aantal punten dat je steeds opnieuw aflegt.
- In de formule, b = y-onderscheppen. Dit is de plaats in uw grafiek waar de lijn de y-as zal oversteken.
-
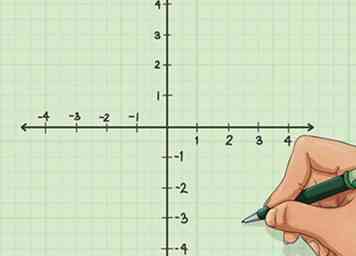 2 Teken je grafiek. Het is het eenvoudigst om een lineaire vergelijking grafisch te maken, omdat u geen cijfers hoeft te berekenen voordat u gaat tekenen. Teken gewoon uw Cartesische coördinaatvlak.
2 Teken je grafiek. Het is het eenvoudigst om een lineaire vergelijking grafisch te maken, omdat u geen cijfers hoeft te berekenen voordat u gaat tekenen. Teken gewoon uw Cartesische coördinaatvlak. -
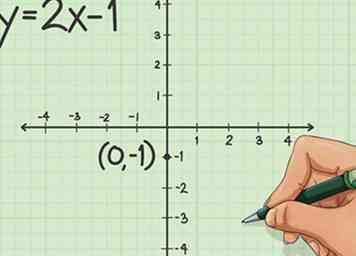 3 Zoek het y-snijpunt (b) in uw grafiek. Als we het voorbeeld van y = 2x-1 gebruiken, kunnen we zien dat '-1' in het punt op de vergelijking staat waar u 'b' zou vinden. Dit maakt '-1' het y-snijpunt.
3 Zoek het y-snijpunt (b) in uw grafiek. Als we het voorbeeld van y = 2x-1 gebruiken, kunnen we zien dat '-1' in het punt op de vergelijking staat waar u 'b' zou vinden. Dit maakt '-1' het y-snijpunt. - Het y-snijpunt wordt altijd getekend met x = 0. Daarom zijn de y-snijpuntcoördinaten (0, -1).
- Plaats een punt op uw grafiek waar het y-snijpunt zou moeten zijn.
-
 4 Vind de helling. In het voorbeeld van y = 2x-1 is de helling het getal waar 'm' wordt gevonden. Dat betekent dat volgens ons voorbeeld de helling '2' is. Helling is echter de opkomst voorbij, dus we hebben de helling nodig om een fractie te zijn. Omdat '2' een geheel getal en een breuk is, is het eenvoudig '2/1'.
4 Vind de helling. In het voorbeeld van y = 2x-1 is de helling het getal waar 'm' wordt gevonden. Dat betekent dat volgens ons voorbeeld de helling '2' is. Helling is echter de opkomst voorbij, dus we hebben de helling nodig om een fractie te zijn. Omdat '2' een geheel getal en een breuk is, is het eenvoudig '2/1'. - Begin met het y-snijpunt om de helling in een grafiek weer te geven. De stijging (aantal openingen) is de teller van de breuk, terwijl de reeks (aantal spaties aan de zijkant) de noemer is van de breuk.
- In ons voorbeeld zouden we de helling plotten door te beginnen bij -1 en vervolgens omhoog te gaan naar 2 en naar rechts 1.
- Een positieve stijging betekent dat u de y-as omhoog gaat, terwijl een negatieve stijging betekent dat u naar beneden gaat. Een positieve run betekent dat je naar rechts van de x-as gaat, terwijl een negatieve run betekent dat je naar links van de x-as gaat.
- U kunt zoveel coördinaten markeren met behulp van de helling als u wilt, maar u moet er minstens één markeren.
-
 5 Teken je lijn. Zodra u met behulp van de helling ten minste één andere coördinaat hebt gemarkeerd, kunt u deze verbinden met uw y-snijpuntcoördinaat om een lijn te vormen. Verleng de lijn naar de randen van de grafiek en voeg pijlpunten toe aan de uiteinden om aan te geven dat het oneindig doorgaat.[1]
5 Teken je lijn. Zodra u met behulp van de helling ten minste één andere coördinaat hebt gemarkeerd, kunt u deze verbinden met uw y-snijpuntcoördinaat om een lijn te vormen. Verleng de lijn naar de randen van de grafiek en voeg pijlpunten toe aan de uiteinden om aan te geven dat het oneindig doorgaat.[1]
Methode twee van zes:
Grafische weergave van ongelijkwaardige ongelijkheden
-
 1 Teken een getallenlijn. Omdat enkelvoudige ongelijkheden op slechts één as voorkomen, hoeft u geen Cartesiaanse coördinaten te gebruiken. Teken in plaats daarvan een eenvoudige cijferlijn.
1 Teken een getallenlijn. Omdat enkelvoudige ongelijkheden op slechts één as voorkomen, hoeft u geen Cartesiaanse coördinaten te gebruiken. Teken in plaats daarvan een eenvoudige cijferlijn. -
 2 Grafiek uw ongelijkheid. Deze zijn vrij eenvoudig, omdat ze maar één coördinaat hebben. Je krijgt een ongelijkheid zoals x <1 voor grafiek. Om dit te doen, zoek eerst '1' op uw nummerregel.
2 Grafiek uw ongelijkheid. Deze zijn vrij eenvoudig, omdat ze maar één coördinaat hebben. Je krijgt een ongelijkheid zoals x <1 voor grafiek. Om dit te doen, zoek eerst '1' op uw nummerregel. - Als u een "groter dan" -symbool krijgt, dat is> of <, teken dan een open cirkel rondom het nummer.
- Als je een "groter dan of gelijk aan" symbool krijgt, ofwel> of <, vul dan de cirkel rond je punt in.
-
 3 Teken je lijn. Gebruik het punt dat u zojuist hebt gemaakt, volg het ongelijkheidsymbool om een lijn te tekenen die de ongelijkheid voorstelt. Als het 'groter dan' het punt is, dan zal de lijn naar rechts gaan. Als het 'kleiner dan' het punt is, wordt de lijn naar links getekend. Voeg een pijl toe aan het einde om aan te geven dat de lijn doorloopt en geen segment is.
3 Teken je lijn. Gebruik het punt dat u zojuist hebt gemaakt, volg het ongelijkheidsymbool om een lijn te tekenen die de ongelijkheid voorstelt. Als het 'groter dan' het punt is, dan zal de lijn naar rechts gaan. Als het 'kleiner dan' het punt is, wordt de lijn naar links getekend. Voeg een pijl toe aan het einde om aan te geven dat de lijn doorloopt en geen segment is. -
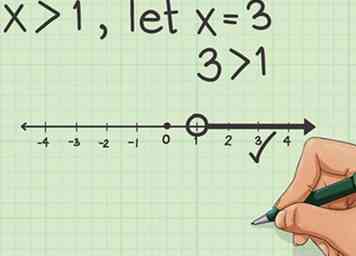 4 Controleer je antwoord. Vervang in een willekeurig cijfer gelijk aan 'x' en markeer het op uw getallenlijn. Als dit nummer op de lijn ligt die u hebt getekend, is uw grafiek correct.
4 Controleer je antwoord. Vervang in een willekeurig cijfer gelijk aan 'x' en markeer het op uw getallenlijn. Als dit nummer op de lijn ligt die u hebt getekend, is uw grafiek correct.
Methode drie van zes:
Grafische lineaire ongelijkheid
-
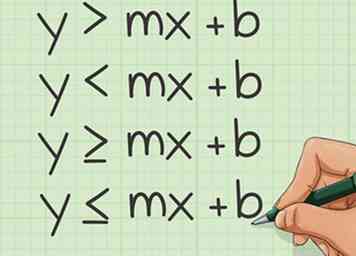 1 Gebruik het formulier voor het onderscheppen van hellingen. Dit is dezelfde formule die wordt gebruikt om reguliere lineaire vergelijkingen te plotten, maar in plaats van dat een '=' teken wordt gebruikt, krijgt u een ongelijkheidsteken te zien. Het ongelijkheidsteken is <,>, <of>.
1 Gebruik het formulier voor het onderscheppen van hellingen. Dit is dezelfde formule die wordt gebruikt om reguliere lineaire vergelijkingen te plotten, maar in plaats van dat een '=' teken wordt gebruikt, krijgt u een ongelijkheidsteken te zien. Het ongelijkheidsteken is <,>, <of>. - De hellingsdoorsnijdingsvorm is y = mx + b, waarbij m = helling en b = y-snijpunt.
- Het aanwezig hebben van een ongelijkheid betekent dat er meerdere oplossingen zijn.
-
 2 Grafiek de ongelijkheid. Zoek het y-snijpunt en de helling om uw coördinaten te markeren. Als we het voorbeeld van y> 1 / 2x + 2 gebruiken, is het y-snijpunt '1'. De helling is ½, wat betekent dat je een punt omhoog gaat en naar de rechter twee punten.
2 Grafiek de ongelijkheid. Zoek het y-snijpunt en de helling om uw coördinaten te markeren. Als we het voorbeeld van y> 1 / 2x + 2 gebruiken, is het y-snijpunt '1'. De helling is ½, wat betekent dat je een punt omhoog gaat en naar de rechter twee punten. -
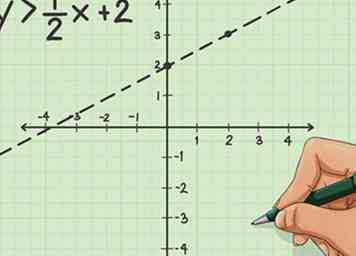 3 Teken je lijn. Controleer voordat u het tekent het ongelijkheidsymbool dat wordt gebruikt. Als het een "groter dan" -symbool is, moet uw regel worden onderbroken. Als het een "groter dan of gelijk aan" -symbool is, zou uw lijn solide moeten zijn.
3 Teken je lijn. Controleer voordat u het tekent het ongelijkheidsymbool dat wordt gebruikt. Als het een "groter dan" -symbool is, moet uw regel worden onderbroken. Als het een "groter dan of gelijk aan" -symbool is, zou uw lijn solide moeten zijn. -
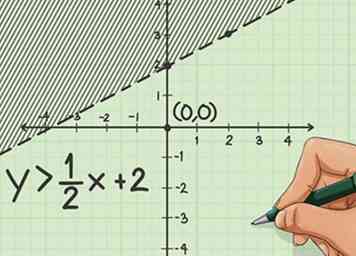 4 Schaduw je grafiek. Omdat er meerdere oplossingen voor een ongelijkheid zijn, moet u alle mogelijke oplossingen in uw grafiek weergeven. Dit betekent dat u de hele grafiek boven of onder uw lijn schaduwt.
4 Schaduw je grafiek. Omdat er meerdere oplossingen voor een ongelijkheid zijn, moet u alle mogelijke oplossingen in uw grafiek weergeven. Dit betekent dat u de hele grafiek boven of onder uw lijn schaduwt. - Kies een coördinaat - de oorsprong op (0,0) is vaak de gemakkelijkste. Zorg ervoor dat je noteert of deze coördinaat boven of onder de lijn ligt die je hebt getekend.
- Vervang deze coördinaten in uw ongelijkheid. Volgens ons voorbeeld zou dit 0> 1/2 (0) +1 zijn. Los deze ongelijkheid op.
- Als het coördinatenpaar een punt boven uw lijn is en het antwoord waar is, dan zou u boven de lijn overschaduwen. Als het antwoord op de ongelijkheid onwaar is, zou je onder de streep in de schaduw zijn. Als de coördinaat onder je lijn ligt en het antwoord waar is, dan schaduw je onder je lijn. Als uw antwoord onjuist is, plaats dan schaduw boven onze lijn.
- In ons voorbeeld is (0,0) onder onze lijn en creëert een foute oplossing wanneer deze wordt vervangen door de ongelijkheid. Dat betekent dat we de rest van de grafiek boven de lijn verduisteren.[2]
Methode vier van de zes:
Kwadratische vergelijkingen grafisch weergeven
-
 1 Onderzoek uw formule. Een kwadratische vergelijking betekent dat u ten minste één variabele in het kwadraat heeft. Het zal meestal worden geschreven in de formule y = ax (kwadraat) + bx + c.
1 Onderzoek uw formule. Een kwadratische vergelijking betekent dat u ten minste één variabele in het kwadraat heeft. Het zal meestal worden geschreven in de formule y = ax (kwadraat) + bx + c. - Het in kaart brengen van een kwadratische vergelijking geeft je een parabool, die een U-vormige curve is.
- U moet ten minste drie punten vinden om het in te delen, te beginnen met de vertex die het hoogste punt is.
-
 2 Zoek 'a', b, 'en' c '. Als we het voorbeeld y = x (kwadraat) + 2x + 1 gebruiken, dan is a = 1, b = 2 en c = 1. Elke letter komt overeen met het getal direct vóór de variabele die het naast in de vergelijking bevat. Als er geen getal staat vóór 'x' in de vergelijking, dan is de variabele gelijk aan '1' omdat wordt aangenomen dat er 1x is.
2 Zoek 'a', b, 'en' c '. Als we het voorbeeld y = x (kwadraat) + 2x + 1 gebruiken, dan is a = 1, b = 2 en c = 1. Elke letter komt overeen met het getal direct vóór de variabele die het naast in de vergelijking bevat. Als er geen getal staat vóór 'x' in de vergelijking, dan is de variabele gelijk aan '1' omdat wordt aangenomen dat er 1x is. -
 3 Vind de vertex. Om de vertex te vinden, het punt in het midden van de parabool, gebruik je de formule -b / 2a. In ons voorbeeld zou deze vergelijking veranderen in -2/2 (1), wat gelijk is aan -1.
3 Vind de vertex. Om de vertex te vinden, het punt in het midden van de parabool, gebruik je de formule -b / 2a. In ons voorbeeld zou deze vergelijking veranderen in -2/2 (1), wat gelijk is aan -1. -
 4 Maak een tafel. U kent nu de vertex, -1, wat een punt op de x-as is. Dit is echter slechts één punt van de hoekpuntcoördinaat. Om de corresponderende y-coördinaat en twee andere punten op je parabool te vinden, moet je een tafel maken.
4 Maak een tafel. U kent nu de vertex, -1, wat een punt op de x-as is. Dit is echter slechts één punt van de hoekpuntcoördinaat. Om de corresponderende y-coördinaat en twee andere punten op je parabool te vinden, moet je een tafel maken. -
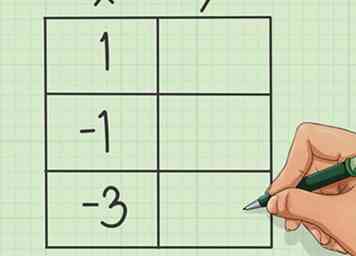 5 Maak een tabel met drie rijen en twee kolommen.
5 Maak een tabel met drie rijen en twee kolommen. - Plaats de x-coördinaat voor de vertex in de kolom bovenaan in het midden.
- Kies nog eens twee x-coördinaten en een gelijk aantal in elke richting (positief en negatief) van het hoekpunt. We kunnen bijvoorbeeld twee en twee naar boven gaan, waarbij we de twee getallen invullen in de andere lege tabelruimten '-3' en '1'.
- U kunt de nummers kiezen die u in de bovenste rij van de tabel wilt invullen, zolang het hele getallen zijn en dezelfde afstand tot de top.
- Als u een duidelijkere grafiek wilt hebben, kunt u vijf coördinaten vinden in plaats van drie. Dit doen is hetzelfde proces als hierboven, maar geef je tabel vijf kolommen in plaats van drie.
-
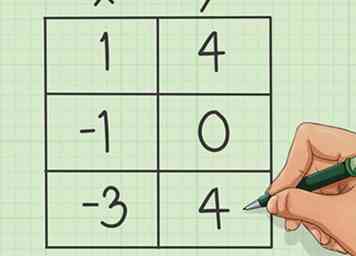 6 Gebruik uw tabel en formule om op te lossen voor de y-coördinaten. Neem één voor één de nummers die u hebt geselecteerd om de x-coördinaten van uw tabel weer te geven en plaats deze in de oorspronkelijke vergelijking. Los op voor 'y'.
6 Gebruik uw tabel en formule om op te lossen voor de y-coördinaten. Neem één voor één de nummers die u hebt geselecteerd om de x-coördinaten van uw tabel weer te geven en plaats deze in de oorspronkelijke vergelijking. Los op voor 'y'. - Naar aanleiding van ons voorbeeld kunnen we onze gekozen coördinaat van '-3' gebruiken om te vervangen door de oorspronkelijke formule van y = x (kwadraat) + 2x + 1. Dit zou veranderen in y = -3 (kwadraat) +2 (3) +1, en geeft een antwoord van y = 4.
- Plaats de nieuwe y-coördinaat onder de x-coördinaat die u in uw tabel hebt gebruikt.
- Los alle drie (of vijf, als u meer wilt) op deze manier coördinaten op.
-
 7 Grafiek de coördinaten. Nu dat je ten minste drie volledige coördinatenparen hebt, markeer ze in je grafiek. Teken een verbinding ze allemaal in een parabool, en je bent klaar!
7 Grafiek de coördinaten. Nu dat je ten minste drie volledige coördinatenparen hebt, markeer ze in je grafiek. Teken een verbinding ze allemaal in een parabool, en je bent klaar!
Methode vijf van zes:
Grafiek van een kwadratische ongelijkheid
-
 1 Los de kwadratische formule op. Een kwadratische ongelijkheid gebruikt dezelfde formule als de kwadratische formule, maar gebruikt in plaats hiervan een ongelijkheidssymbool. Het zal er bijvoorbeeld uitzien als y
1 Los de kwadratische formule op. Een kwadratische ongelijkheid gebruikt dezelfde formule als de kwadratische formule, maar gebruikt in plaats hiervan een ongelijkheidssymbool. Het zal er bijvoorbeeld uitzien als y -
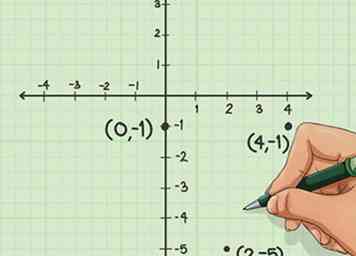 2 Markeer de coördinaten in uw grafiek. Hoewel je genoeg punten hebt om je complete parabool te maken, teken dan nog niet de vorm.
2 Markeer de coördinaten in uw grafiek. Hoewel je genoeg punten hebt om je complete parabool te maken, teken dan nog niet de vorm. -
 3 Verbind de punten op uw grafiek. Omdat je een kwadratische ongelijkheid in een grafiek tekent, zal de lijn die je tekent een beetje anders zijn.
3 Verbind de punten op uw grafiek. Omdat je een kwadratische ongelijkheid in een grafiek tekent, zal de lijn die je tekent een beetje anders zijn. - Als uw ongelijkheidsymbool "groter dan" of "kleiner dan" (> of <) is, tekent u een streepjeslijn tussen de coördinaten.
- Als uw ongelijkheidsymbool "groter dan of gelijk aan" of "kleiner dan of gelijk aan" is (> of <), dan zal de lijn die u tekent, solide zijn.
- Beëindig uw lijnen met pijlpunten om aan te geven dat de oplossingen verder reiken dan het bereik van uw grafiek.
-
 4 Schaduw de grafiek. Als u meerdere oplossingen wilt weergeven, stelt u het gedeelte van de grafiek in waarop de oplossing kan worden gevonden. Als u wilt weten welk deel van de grafiek moet worden gearceerd, test u een paar coördinaten in uw formule. Een eenvoudig in te stellen set is (0,0). Merk op of deze coördinaten binnen of buiten je parabool liggen of niet.
4 Schaduw de grafiek. Als u meerdere oplossingen wilt weergeven, stelt u het gedeelte van de grafiek in waarop de oplossing kan worden gevonden. Als u wilt weten welk deel van de grafiek moet worden gearceerd, test u een paar coördinaten in uw formule. Een eenvoudig in te stellen set is (0,0). Merk op of deze coördinaten binnen of buiten je parabool liggen of niet. - Los de ongelijkheid op met de coördinaten die je hebt gekozen. Als we een voorbeeld van y> x (kwadraat) -4x-1 gebruiken en de coördinaten (0,0) vervangen, verandert het in 0> 0 (kwadraat) -4 (0) -1.
- Als de oplossing hiervoor klopt en de coördinaten zich in de parabool bevinden, schaduw in de parabool. Als de oplossing vals is, schaduw buiten de parabool.
- Als de oplossing hiervoor klopt en de coördinaten zich buiten de parabool bevinden, schaduw de buitenkant van de parabool. Als de oplossing vals is, schaduw binnen de parabool.[3]
Methode Zes van de zes:
Een absolute-waarde vergelijking plotten
-
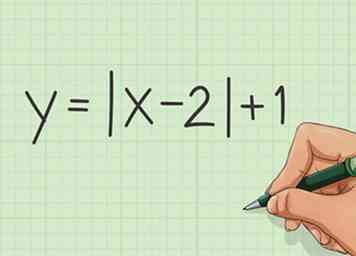 1 Onderzoek uw vergelijking. De meest elementaire absolute waarde-vergelijking verschijnt als y = | x |. Het kan echter gaan om andere getallen of variabelen.
1 Onderzoek uw vergelijking. De meest elementaire absolute waarde-vergelijking verschijnt als y = | x |. Het kan echter gaan om andere getallen of variabelen. -
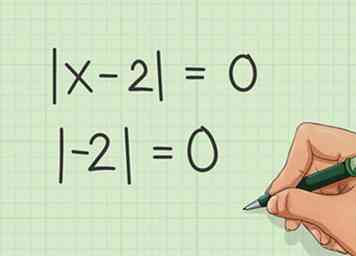 2 Maak de absolute waarde gelijk aan 0. Om dit te doen, maakt u alles in de absolute waardelijnen | | = 0. Als we het voorbeeld y = | x-2 | +1 gebruiken, krijgen we de absolute waarde door | x-2 | = 0 te maken. Dan wordt de absolute waarde 2.
2 Maak de absolute waarde gelijk aan 0. Om dit te doen, maakt u alles in de absolute waardelijnen | | = 0. Als we het voorbeeld y = | x-2 | +1 gebruiken, krijgen we de absolute waarde door | x-2 | = 0 te maken. Dan wordt de absolute waarde 2. - De absolute waarde is het aantal punten van | x | op '0' op een getallenlijn. Dus de absolute waarde van | 2 | is 2 en de absolute waarde van | -2 | is ook twee. Dit komt omdat in beide gevallen '2' en '-2' zich op 2 stappen van nul op de getallenlijn bevinden.
- Je hebt misschien een absolute-waardevergelijking waarbij 'x' alleen staat. In dat geval is de absolute waarde '0'. Bijvoorbeeld, y = | x | +3 verandert in y = | 0 | +3, wat gelijk is aan '3'.
-
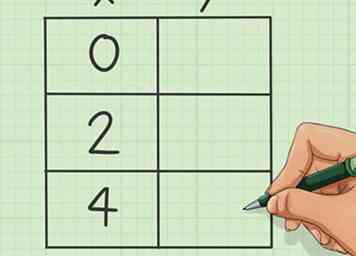 3 Maak een tafel. U wilt dat het drie rijen en twee kolommen heeft.
3 Maak een tafel. U wilt dat het drie rijen en twee kolommen heeft. - Zet de eerste absolute waardecoördinaat in de kolom in het midden bovenaan voor 'X'.
- Kies twee andere nummers op gelijke afstand van uw x-coördinaat in elke richting (positief en negatief).Als | x | = 0, beweeg dan een gelijk aantal spaties op en neer vanaf '0'.
- U kunt elk getal kiezen, hoewel degene die zich in de buurt van de x-coördinaat bevinden, het nuttigst zijn. Ze moeten ook hele cijfers zijn.
-
 4 Los de ongelijkheid op. Je moet de y-coördinaat vinden die overeenkomt met de drie x-coördinaten die je hebt. Om dit te doen, vervangt u de x-coördinaatwaarden in de ongelijkheid en lost u op voor 'y'. Vul deze antwoorden in op uw tafel.
4 Los de ongelijkheid op. Je moet de y-coördinaat vinden die overeenkomt met de drie x-coördinaten die je hebt. Om dit te doen, vervangt u de x-coördinaatwaarden in de ongelijkheid en lost u op voor 'y'. Vul deze antwoorden in op uw tafel. -
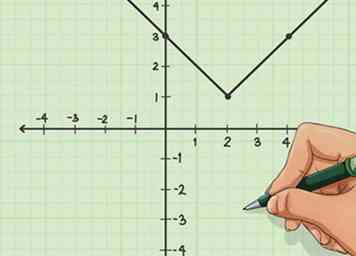 5 Grafiek de punten. Je hebt maar drie punten nodig om een absolute-waardevergelijking te tekenen, maar je kunt er meer gebruiken als je dat wilt. Een absolute waardevergelijking zal altijd een "V" -vorm op uw grafiek vormen. Voeg pijlen toe aan de uiteinden om aan te geven dat de lijn verder reikt dan de rand van uw grafiek.[4]
5 Grafiek de punten. Je hebt maar drie punten nodig om een absolute-waardevergelijking te tekenen, maar je kunt er meer gebruiken als je dat wilt. Een absolute waardevergelijking zal altijd een "V" -vorm op uw grafiek vormen. Voeg pijlen toe aan de uiteinden om aan te geven dat de lijn verder reikt dan de rand van uw grafiek.[4]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Gebruik de formule y = mx + b. Als u een lineaire vergelijking wilt tekenen, moet u alleen de variabelen in deze formule vervangen.
1 Gebruik de formule y = mx + b. Als u een lineaire vergelijking wilt tekenen, moet u alleen de variabelen in deze formule vervangen.  2 Teken je grafiek. Het is het eenvoudigst om een lineaire vergelijking grafisch te maken, omdat u geen cijfers hoeft te berekenen voordat u gaat tekenen. Teken gewoon uw Cartesische coördinaatvlak.
2 Teken je grafiek. Het is het eenvoudigst om een lineaire vergelijking grafisch te maken, omdat u geen cijfers hoeft te berekenen voordat u gaat tekenen. Teken gewoon uw Cartesische coördinaatvlak. 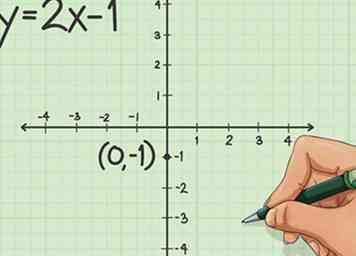 3 Zoek het y-snijpunt (b) in uw grafiek. Als we het voorbeeld van y = 2x-1 gebruiken, kunnen we zien dat '-1' in het punt op de vergelijking staat waar u 'b' zou vinden. Dit maakt '-1' het y-snijpunt.
3 Zoek het y-snijpunt (b) in uw grafiek. Als we het voorbeeld van y = 2x-1 gebruiken, kunnen we zien dat '-1' in het punt op de vergelijking staat waar u 'b' zou vinden. Dit maakt '-1' het y-snijpunt.  4 Vind de helling. In het voorbeeld van y = 2x-1 is de helling het getal waar 'm' wordt gevonden. Dat betekent dat volgens ons voorbeeld de helling '2' is. Helling is echter de opkomst voorbij, dus we hebben de helling nodig om een fractie te zijn. Omdat '2' een geheel getal en een breuk is, is het eenvoudig '2/1'.
4 Vind de helling. In het voorbeeld van y = 2x-1 is de helling het getal waar 'm' wordt gevonden. Dat betekent dat volgens ons voorbeeld de helling '2' is. Helling is echter de opkomst voorbij, dus we hebben de helling nodig om een fractie te zijn. Omdat '2' een geheel getal en een breuk is, is het eenvoudig '2/1'.  5 Teken je lijn. Zodra u met behulp van de helling ten minste één andere coördinaat hebt gemarkeerd, kunt u deze verbinden met uw y-snijpuntcoördinaat om een lijn te vormen. Verleng de lijn naar de randen van de grafiek en voeg pijlpunten toe aan de uiteinden om aan te geven dat het oneindig doorgaat.[1]
5 Teken je lijn. Zodra u met behulp van de helling ten minste één andere coördinaat hebt gemarkeerd, kunt u deze verbinden met uw y-snijpuntcoördinaat om een lijn te vormen. Verleng de lijn naar de randen van de grafiek en voeg pijlpunten toe aan de uiteinden om aan te geven dat het oneindig doorgaat.[1]  1 Teken een getallenlijn. Omdat enkelvoudige ongelijkheden op slechts één as voorkomen, hoeft u geen Cartesiaanse coördinaten te gebruiken. Teken in plaats daarvan een eenvoudige cijferlijn.
1 Teken een getallenlijn. Omdat enkelvoudige ongelijkheden op slechts één as voorkomen, hoeft u geen Cartesiaanse coördinaten te gebruiken. Teken in plaats daarvan een eenvoudige cijferlijn.  2 Grafiek uw ongelijkheid. Deze zijn vrij eenvoudig, omdat ze maar één coördinaat hebben. Je krijgt een ongelijkheid zoals x <1 voor grafiek. Om dit te doen, zoek eerst '1' op uw nummerregel.
2 Grafiek uw ongelijkheid. Deze zijn vrij eenvoudig, omdat ze maar één coördinaat hebben. Je krijgt een ongelijkheid zoals x <1 voor grafiek. Om dit te doen, zoek eerst '1' op uw nummerregel.  3 Teken je lijn. Gebruik het punt dat u zojuist hebt gemaakt, volg het ongelijkheidsymbool om een lijn te tekenen die de ongelijkheid voorstelt. Als het 'groter dan' het punt is, dan zal de lijn naar rechts gaan. Als het 'kleiner dan' het punt is, wordt de lijn naar links getekend. Voeg een pijl toe aan het einde om aan te geven dat de lijn doorloopt en geen segment is.
3 Teken je lijn. Gebruik het punt dat u zojuist hebt gemaakt, volg het ongelijkheidsymbool om een lijn te tekenen die de ongelijkheid voorstelt. Als het 'groter dan' het punt is, dan zal de lijn naar rechts gaan. Als het 'kleiner dan' het punt is, wordt de lijn naar links getekend. Voeg een pijl toe aan het einde om aan te geven dat de lijn doorloopt en geen segment is. 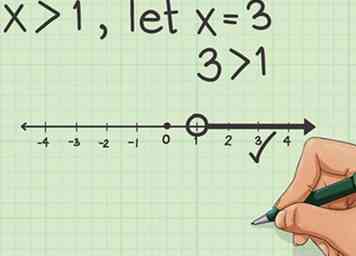 4 Controleer je antwoord. Vervang in een willekeurig cijfer gelijk aan 'x' en markeer het op uw getallenlijn. Als dit nummer op de lijn ligt die u hebt getekend, is uw grafiek correct.
4 Controleer je antwoord. Vervang in een willekeurig cijfer gelijk aan 'x' en markeer het op uw getallenlijn. Als dit nummer op de lijn ligt die u hebt getekend, is uw grafiek correct. 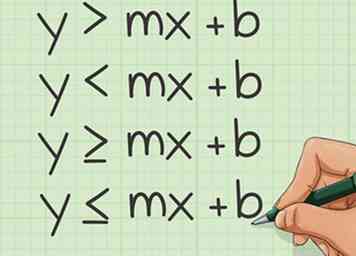 1 Gebruik het formulier voor het onderscheppen van hellingen. Dit is dezelfde formule die wordt gebruikt om reguliere lineaire vergelijkingen te plotten, maar in plaats van dat een '=' teken wordt gebruikt, krijgt u een ongelijkheidsteken te zien. Het ongelijkheidsteken is <,>, <of>.
1 Gebruik het formulier voor het onderscheppen van hellingen. Dit is dezelfde formule die wordt gebruikt om reguliere lineaire vergelijkingen te plotten, maar in plaats van dat een '=' teken wordt gebruikt, krijgt u een ongelijkheidsteken te zien. Het ongelijkheidsteken is <,>, <of>.  2 Grafiek de ongelijkheid. Zoek het y-snijpunt en de helling om uw coördinaten te markeren. Als we het voorbeeld van y> 1 / 2x + 2 gebruiken, is het y-snijpunt '1'. De helling is ½, wat betekent dat je een punt omhoog gaat en naar de rechter twee punten.
2 Grafiek de ongelijkheid. Zoek het y-snijpunt en de helling om uw coördinaten te markeren. Als we het voorbeeld van y> 1 / 2x + 2 gebruiken, is het y-snijpunt '1'. De helling is ½, wat betekent dat je een punt omhoog gaat en naar de rechter twee punten.  3 Teken je lijn. Controleer voordat u het tekent het ongelijkheidsymbool dat wordt gebruikt. Als het een "groter dan" -symbool is, moet uw regel worden onderbroken. Als het een "groter dan of gelijk aan" -symbool is, zou uw lijn solide moeten zijn.
3 Teken je lijn. Controleer voordat u het tekent het ongelijkheidsymbool dat wordt gebruikt. Als het een "groter dan" -symbool is, moet uw regel worden onderbroken. Als het een "groter dan of gelijk aan" -symbool is, zou uw lijn solide moeten zijn.  4 Schaduw je grafiek. Omdat er meerdere oplossingen voor een ongelijkheid zijn, moet u alle mogelijke oplossingen in uw grafiek weergeven. Dit betekent dat u de hele grafiek boven of onder uw lijn schaduwt.
4 Schaduw je grafiek. Omdat er meerdere oplossingen voor een ongelijkheid zijn, moet u alle mogelijke oplossingen in uw grafiek weergeven. Dit betekent dat u de hele grafiek boven of onder uw lijn schaduwt.  1 Onderzoek uw formule. Een kwadratische vergelijking betekent dat u ten minste één variabele in het kwadraat heeft. Het zal meestal worden geschreven in de formule y = ax (kwadraat) + bx + c.
1 Onderzoek uw formule. Een kwadratische vergelijking betekent dat u ten minste één variabele in het kwadraat heeft. Het zal meestal worden geschreven in de formule y = ax (kwadraat) + bx + c.  2 Zoek 'a', b, 'en' c '. Als we het voorbeeld y = x (kwadraat) + 2x + 1 gebruiken, dan is a = 1, b = 2 en c = 1. Elke letter komt overeen met het getal direct vóór de variabele die het naast in de vergelijking bevat. Als er geen getal staat vóór 'x' in de vergelijking, dan is de variabele gelijk aan '1' omdat wordt aangenomen dat er 1x is.
2 Zoek 'a', b, 'en' c '. Als we het voorbeeld y = x (kwadraat) + 2x + 1 gebruiken, dan is a = 1, b = 2 en c = 1. Elke letter komt overeen met het getal direct vóór de variabele die het naast in de vergelijking bevat. Als er geen getal staat vóór 'x' in de vergelijking, dan is de variabele gelijk aan '1' omdat wordt aangenomen dat er 1x is.  3 Vind de vertex. Om de vertex te vinden, het punt in het midden van de parabool, gebruik je de formule -b / 2a. In ons voorbeeld zou deze vergelijking veranderen in -2/2 (1), wat gelijk is aan -1.
3 Vind de vertex. Om de vertex te vinden, het punt in het midden van de parabool, gebruik je de formule -b / 2a. In ons voorbeeld zou deze vergelijking veranderen in -2/2 (1), wat gelijk is aan -1.  4 Maak een tafel. U kent nu de vertex, -1, wat een punt op de x-as is. Dit is echter slechts één punt van de hoekpuntcoördinaat. Om de corresponderende y-coördinaat en twee andere punten op je parabool te vinden, moet je een tafel maken.
4 Maak een tafel. U kent nu de vertex, -1, wat een punt op de x-as is. Dit is echter slechts één punt van de hoekpuntcoördinaat. Om de corresponderende y-coördinaat en twee andere punten op je parabool te vinden, moet je een tafel maken.  5 Maak een tabel met drie rijen en twee kolommen.
5 Maak een tabel met drie rijen en twee kolommen.  6 Gebruik uw tabel en formule om op te lossen voor de y-coördinaten. Neem één voor één de nummers die u hebt geselecteerd om de x-coördinaten van uw tabel weer te geven en plaats deze in de oorspronkelijke vergelijking. Los op voor 'y'.
6 Gebruik uw tabel en formule om op te lossen voor de y-coördinaten. Neem één voor één de nummers die u hebt geselecteerd om de x-coördinaten van uw tabel weer te geven en plaats deze in de oorspronkelijke vergelijking. Los op voor 'y'.  7 Grafiek de coördinaten. Nu dat je ten minste drie volledige coördinatenparen hebt, markeer ze in je grafiek. Teken een verbinding ze allemaal in een parabool, en je bent klaar!
7 Grafiek de coördinaten. Nu dat je ten minste drie volledige coördinatenparen hebt, markeer ze in je grafiek. Teken een verbinding ze allemaal in een parabool, en je bent klaar!  1 Los de kwadratische formule op. Een kwadratische ongelijkheid gebruikt dezelfde formule als de kwadratische formule, maar gebruikt in plaats hiervan een ongelijkheidssymbool. Het zal er bijvoorbeeld uitzien als y
1 Los de kwadratische formule op. Een kwadratische ongelijkheid gebruikt dezelfde formule als de kwadratische formule, maar gebruikt in plaats hiervan een ongelijkheidssymbool. Het zal er bijvoorbeeld uitzien als y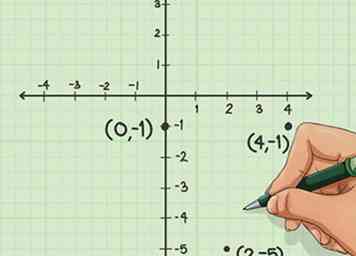 2 Markeer de coördinaten in uw grafiek. Hoewel je genoeg punten hebt om je complete parabool te maken, teken dan nog niet de vorm.
2 Markeer de coördinaten in uw grafiek. Hoewel je genoeg punten hebt om je complete parabool te maken, teken dan nog niet de vorm.  3 Verbind de punten op uw grafiek. Omdat je een kwadratische ongelijkheid in een grafiek tekent, zal de lijn die je tekent een beetje anders zijn.
3 Verbind de punten op uw grafiek. Omdat je een kwadratische ongelijkheid in een grafiek tekent, zal de lijn die je tekent een beetje anders zijn.  4 Schaduw de grafiek. Als u meerdere oplossingen wilt weergeven, stelt u het gedeelte van de grafiek in waarop de oplossing kan worden gevonden. Als u wilt weten welk deel van de grafiek moet worden gearceerd, test u een paar coördinaten in uw formule. Een eenvoudig in te stellen set is (0,0). Merk op of deze coördinaten binnen of buiten je parabool liggen of niet.
4 Schaduw de grafiek. Als u meerdere oplossingen wilt weergeven, stelt u het gedeelte van de grafiek in waarop de oplossing kan worden gevonden. Als u wilt weten welk deel van de grafiek moet worden gearceerd, test u een paar coördinaten in uw formule. Een eenvoudig in te stellen set is (0,0). Merk op of deze coördinaten binnen of buiten je parabool liggen of niet. 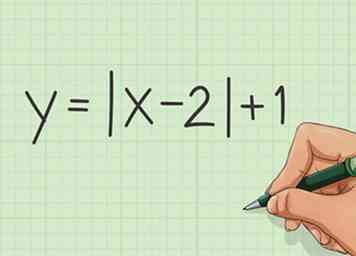 1 Onderzoek uw vergelijking. De meest elementaire absolute waarde-vergelijking verschijnt als y = | x |. Het kan echter gaan om andere getallen of variabelen.
1 Onderzoek uw vergelijking. De meest elementaire absolute waarde-vergelijking verschijnt als y = | x |. Het kan echter gaan om andere getallen of variabelen. 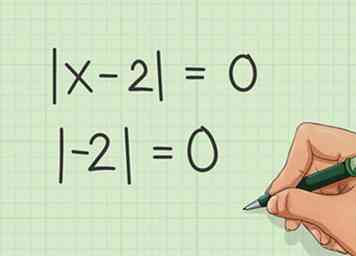 2 Maak de absolute waarde gelijk aan 0. Om dit te doen, maakt u alles in de absolute waardelijnen | | = 0. Als we het voorbeeld y = | x-2 | +1 gebruiken, krijgen we de absolute waarde door | x-2 | = 0 te maken. Dan wordt de absolute waarde 2.
2 Maak de absolute waarde gelijk aan 0. Om dit te doen, maakt u alles in de absolute waardelijnen | | = 0. Als we het voorbeeld y = | x-2 | +1 gebruiken, krijgen we de absolute waarde door | x-2 | = 0 te maken. Dan wordt de absolute waarde 2.  3 Maak een tafel. U wilt dat het drie rijen en twee kolommen heeft.
3 Maak een tafel. U wilt dat het drie rijen en twee kolommen heeft.  4 Los de ongelijkheid op. Je moet de y-coördinaat vinden die overeenkomt met de drie x-coördinaten die je hebt. Om dit te doen, vervangt u de x-coördinaatwaarden in de ongelijkheid en lost u op voor 'y'. Vul deze antwoorden in op uw tafel.
4 Los de ongelijkheid op. Je moet de y-coördinaat vinden die overeenkomt met de drie x-coördinaten die je hebt. Om dit te doen, vervangt u de x-coördinaatwaarden in de ongelijkheid en lost u op voor 'y'. Vul deze antwoorden in op uw tafel.  5 Grafiek de punten. Je hebt maar drie punten nodig om een absolute-waardevergelijking te tekenen, maar je kunt er meer gebruiken als je dat wilt. Een absolute waardevergelijking zal altijd een "V" -vorm op uw grafiek vormen. Voeg pijlen toe aan de uiteinden om aan te geven dat de lijn verder reikt dan de rand van uw grafiek.[4]
5 Grafiek de punten. Je hebt maar drie punten nodig om een absolute-waardevergelijking te tekenen, maar je kunt er meer gebruiken als je dat wilt. Een absolute waardevergelijking zal altijd een "V" -vorm op uw grafiek vormen. Voeg pijlen toe aan de uiteinden om aan te geven dat de lijn verder reikt dan de rand van uw grafiek.[4]