Een vector is een geometrisch object met richting en magnitude. Het kan worden gerepresenteerd als een lijnsegment met een beginpunt (startpunt) aan het ene uiteinde en een pijl aan het andere uiteinde, zodanig dat de lengte van het lijnsegment de grootte van de vector is en de pijl de richting van de vector aangeeft . Vectornormalisatie is een veel voorkomende oefening in de wiskunde en het heeft ook praktische toepassingen in computergraphics.
Methode één van de vijf:
Definieer voorwaarden
-
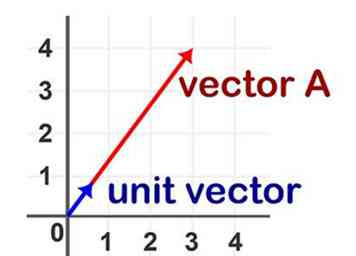 1 Definieer een eenheidsvector. De eenheidsvector van een vector A is de vector met hetzelfde beginpunt en dezelfde richting als A, maar met een lengte van 1 eenheid. Het kan wiskundig worden bewezen dat er één en slechts één eenheidsvector is voor elke gegeven vector A.
1 Definieer een eenheidsvector. De eenheidsvector van een vector A is de vector met hetzelfde beginpunt en dezelfde richting als A, maar met een lengte van 1 eenheid. Het kan wiskundig worden bewezen dat er één en slechts één eenheidsvector is voor elke gegeven vector A. -
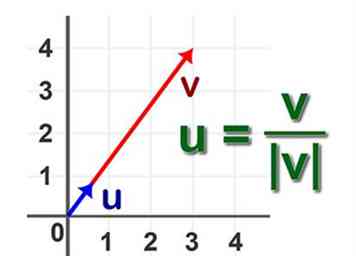 2 Definieer de normalisatie van een vector. Dit is het proces van het identificeren van de eenheidsvector voor een gegeven vector A.
2 Definieer de normalisatie van een vector. Dit is het proces van het identificeren van de eenheidsvector voor een gegeven vector A. -
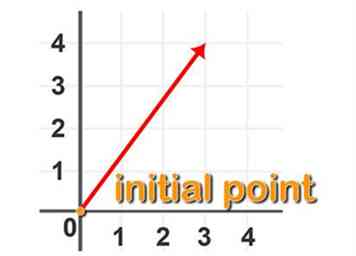 3 Definieer een gebonden vector. Een gebonden vector in de Cartesiaanse ruimte heeft zijn beginpunt aan de oorsprong van het coördinatensysteem, uitgedrukt als (0,0) in twee dimensies. Hiermee kunt u een vector alleen in termen van zijn eindpunt identificeren.
3 Definieer een gebonden vector. Een gebonden vector in de Cartesiaanse ruimte heeft zijn beginpunt aan de oorsprong van het coördinatensysteem, uitgedrukt als (0,0) in twee dimensies. Hiermee kunt u een vector alleen in termen van zijn eindpunt identificeren. -
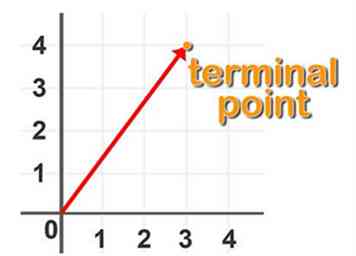 4 Beschrijf vectornotatie. Door onszelf te beperken tot gebonden vectoren, A = (x, y) waar het coördinatenpaar (x, y) de locatie van het eindpunt voor vector A aangeeft.
4 Beschrijf vectornotatie. Door onszelf te beperken tot gebonden vectoren, A = (x, y) waar het coördinatenpaar (x, y) de locatie van het eindpunt voor vector A aangeeft.
Methode twee van vijf:
Analyseer de doelstelling
-
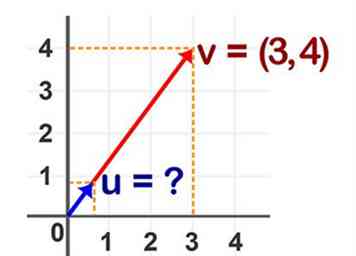 1 Breng de bekende waarden tot stand. Uit de definitie van de eenheidsvector weten we dat het beginpunt en de richting van de eenheidsvector dezelfde is als de gegeven vector A. Verder weten we dat de lengte van de eenheidsvector 1 is.
1 Breng de bekende waarden tot stand. Uit de definitie van de eenheidsvector weten we dat het beginpunt en de richting van de eenheidsvector dezelfde is als de gegeven vector A. Verder weten we dat de lengte van de eenheidsvector 1 is. -
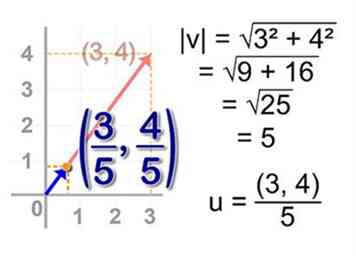 2 Bepaal de onbekende waarde. De enige variabele die we moeten berekenen is het eindpunt van de eenheidsvector.
2 Bepaal de onbekende waarde. De enige variabele die we moeten berekenen is het eindpunt van de eenheidsvector.
Methode drie van vijf:
Leid een oplossing voor de unitvector
- Zoek het eindpunt voor de eenheidsvector van vector A = (x, y). Uit de evenredigheid van soortgelijke driehoeken weet u dat elke vector met dezelfde richting als vector A een eindpunt (x / c, y / c) heeft voor sommige c. Bovendien weet je dat de lengte van de eenheidsvector 1 is. Daarom, volgens de stelling van Pythagoras, [x ^ 2 / c ^ 2 + y ^ 2 / c ^ 2] ^ (1/2) = 1 -> [(x ^ 2 + y ^ 2) / c ^ 2] ^ (1/2) -> (x ^ 2 + y ^ 2) ^ (1/2) / c = 1 -> c = (x ^ 2 + y ^ 2) ^ (1/2). Daarom wordt de eenheidsvector u voor de vector A = (x, y) gegeven als u = (x / (x ^ 2 + y ^ 2) ^ (1/2), y / (x ^ 2 + y ^ 2 ) ^ (1/2))

Methode vier van vijf:
Normaliseer een Vector in 2 Dimensional Space
- Laat vector A een vector zijn met zijn beginpunt op de oorsprong en het eindpunt op (2,3), zodanig dat A = (2,3). Bereken de eenheidsvector u = (x / (x ^ 2 + y ^ 2) ^ (1/2), y / (x ^ 2 + y ^ 2) ^ (1/2)) = (2 / (2 ^ 2 + 3 ^ 2) ^ (1/2), 3 / (2 ^ 2 + 3 ^ 2) ^ (1/2)) = (2 / (13 ^ (1/2)), 3 / (13 ^ (1/2))). Daarom normaliseert A = (2,3) tot u = (2 / (13 ^ (1/2)), 3 / (13 ^ (1/2))).

Methode vijf van vijf:
Een vector in een nimensionale ruimte normaliseren
- Generaliseer de vergelijking voor vectornormalisatie in de ruimte van elke dimensie. Een vector A (a, b, c, ...), u = (a / z, b / z, c / z, ...) waarbij z = (a ^ 2 + b ^ 2 + c ^ 2 ...) ^ (1 / 2).
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Definieer een eenheidsvector. De eenheidsvector van een vector A is de vector met hetzelfde beginpunt en dezelfde richting als A, maar met een lengte van 1 eenheid. Het kan wiskundig worden bewezen dat er één en slechts één eenheidsvector is voor elke gegeven vector A.
1 Definieer een eenheidsvector. De eenheidsvector van een vector A is de vector met hetzelfde beginpunt en dezelfde richting als A, maar met een lengte van 1 eenheid. Het kan wiskundig worden bewezen dat er één en slechts één eenheidsvector is voor elke gegeven vector A.  2 Definieer de normalisatie van een vector. Dit is het proces van het identificeren van de eenheidsvector voor een gegeven vector A.
2 Definieer de normalisatie van een vector. Dit is het proces van het identificeren van de eenheidsvector voor een gegeven vector A.  3 Definieer een gebonden vector. Een gebonden vector in de Cartesiaanse ruimte heeft zijn beginpunt aan de oorsprong van het coördinatensysteem, uitgedrukt als (0,0) in twee dimensies. Hiermee kunt u een vector alleen in termen van zijn eindpunt identificeren.
3 Definieer een gebonden vector. Een gebonden vector in de Cartesiaanse ruimte heeft zijn beginpunt aan de oorsprong van het coördinatensysteem, uitgedrukt als (0,0) in twee dimensies. Hiermee kunt u een vector alleen in termen van zijn eindpunt identificeren.  4 Beschrijf vectornotatie. Door onszelf te beperken tot gebonden vectoren, A = (x, y) waar het coördinatenpaar (x, y) de locatie van het eindpunt voor vector A aangeeft.
4 Beschrijf vectornotatie. Door onszelf te beperken tot gebonden vectoren, A = (x, y) waar het coördinatenpaar (x, y) de locatie van het eindpunt voor vector A aangeeft.  1 Breng de bekende waarden tot stand. Uit de definitie van de eenheidsvector weten we dat het beginpunt en de richting van de eenheidsvector dezelfde is als de gegeven vector A. Verder weten we dat de lengte van de eenheidsvector 1 is.
1 Breng de bekende waarden tot stand. Uit de definitie van de eenheidsvector weten we dat het beginpunt en de richting van de eenheidsvector dezelfde is als de gegeven vector A. Verder weten we dat de lengte van de eenheidsvector 1 is.  2 Bepaal de onbekende waarde. De enige variabele die we moeten berekenen is het eindpunt van de eenheidsvector.
2 Bepaal de onbekende waarde. De enige variabele die we moeten berekenen is het eindpunt van de eenheidsvector.