Om de vergelijking van een lijn te vinden, hebt u enkele opties waaruit u kunt kiezen, afhankelijk van wat u hebt gekregen. Je zult uiteindelijk altijd op zijn minst nodig hebben een punt op de lijn en de helling om een vergelijking te berekenen. Hoewel de taak soms overweldigend overkomt, zijn de verschillende processen echt vrij eenvoudig als je eenmaal weet waarnaar je op zoek bent. Zodra je het punt en de helling van je lijn hebt, is de rest gewoon aan te sluiten en opnieuw te ordenen.
Methode één van de vier:
De gegeven punten gebruiken voor een helling
-
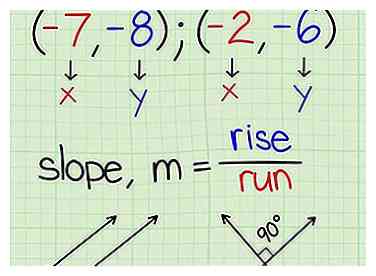 1 Kijk of je 2 punten of 1 punt en de helling krijgt. Als je 1 punt op de lijn en zijn helling krijgt, kun je doorgaan naar de Eindig met de Point-Slope-formule methode. Anders moet u de twee gegeven punten gebruiken om de helling van de lijn te vinden.
1 Kijk of je 2 punten of 1 punt en de helling krijgt. Als je 1 punt op de lijn en zijn helling krijgt, kun je doorgaan naar de Eindig met de Point-Slope-formule methode. Anders moet u de twee gegeven punten gebruiken om de helling van de lijn te vinden. - Ze zullen de vorm hebben van (X1, y1) en (X2, y2).
-
 2 Gebruik andere informatie om punten op de lijn te krijgen. Sommige problemen vereisen interpretatie van informatie over de lijn om een punt op de lijn te krijgen. Als u bijvoorbeeld wordt verteld dat de lijn door de lijn loopt oorsprong, dat weet je (0, 0) is een punt op de lijn!
2 Gebruik andere informatie om punten op de lijn te krijgen. Sommige problemen vereisen interpretatie van informatie over de lijn om een punt op de lijn te krijgen. Als u bijvoorbeeld wordt verteld dat de lijn door de lijn loopt oorsprong, dat weet je (0, 0) is een punt op de lijn! - Bekijk grafieken die bij de vraag horen voor het geval u een onderschepping zou moeten vinden (waar de lijn de kruising doorkruist) x-as of Y-as) van de foto. Een x-as zou in de vorm zijn (a, 0) terwijl een y-intercept zou zijn (0, b).
- U kunt ook eenvoudigweg worden verteld dat de lijn op een bepaald punt een as kruist. Dit betekent het instellen van het overeenkomstige X of Y waarde naar 0 en combineer het met het gegeven nummer waar de lijn kruist.
-
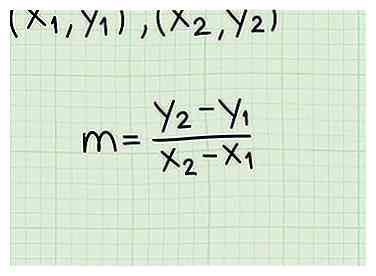 3 Bereken de helling van de lijn door de twee punten. De vergelijking voor de helling is m = (y2 - y1) / (x2 - x1). Door simpelweg uw coördinaatpunten in te pluggen en op te lossen, kent u nu de helling van de vergelijking.
3 Bereken de helling van de lijn door de twee punten. De vergelijking voor de helling is m = (y2 - y1) / (x2 - x1). Door simpelweg uw coördinaatpunten in te pluggen en op te lossen, kent u nu de helling van de vergelijking. - De helling wordt bijna altijd aangeduid als m. Houd er rekening mee dat dit wel positief of negatief kan zijn.
- Vanaf dit punt heb je alleen een van de punten nodig die je hebt gevonden met de helling. Als iemand klaarblijkelijk eenvoudiger is, ga daar dan mee akkoord. Bijvoorbeeld, als uw lijn de oorsprong, het oplossen van de rest van het probleem met (0, 0) is een beetje sneller.
Methode twee van vier:
De helling van een andere lijn halen
-
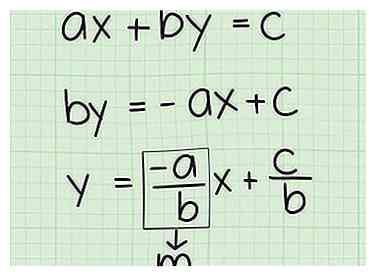 1 Gebruik dezelfde helling als de andere lijn evenwijdig is. Parallelle lijnen delen dezelfde helling, dus alles wat u hoeft te doen is de vergelijking uit die lijn gebruiken om de helling voor uw eerste lijn te krijgen.
1 Gebruik dezelfde helling als de andere lijn evenwijdig is. Parallelle lijnen delen dezelfde helling, dus alles wat u hoeft te doen is de vergelijking uit die lijn gebruiken om de helling voor uw eerste lijn te krijgen. - Gebruik algebra om de vergelijking van de lijn in te regelen helling-onderscheppen vorm welke is y = mx + b. Als Y is alleen aan de linkerkant, dan m is de helling van beide lijnen, en b zal gewoon de y-intercept van die lijn.
- Na het ordenen van de vergelijking, realiseer je dat je helling positief, negatief of zelfs een fractie in plaats van een geheel getal kan zijn.
-
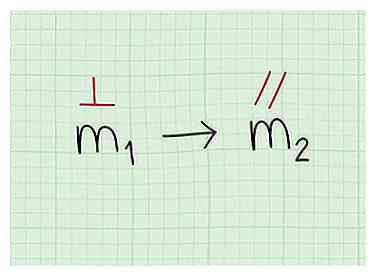 2 Zoek de helling van een loodlijn. Vaak zullen vragen je een loodrecht regel naar de regel waarvoor u een vergelijking wilt. Hier gebruikt u dezelfde concepten als eerder om de helling van de loodlijn te bepalen.
2 Zoek de helling van een loodlijn. Vaak zullen vragen je een loodrecht regel naar de regel waarvoor u een vergelijking wilt. Hier gebruikt u dezelfde concepten als eerder om de helling van de loodlijn te bepalen. - Simpelweg de vergelijking die met algebra wordt gegeven herschikken om de vergelijking te krijgen helling-onderscheppen vorm (y = mx + b).
-
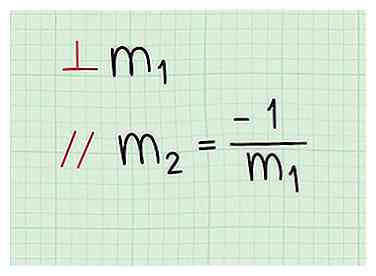 3 Gebruik de negatieve reciprook van de helling van de loodlijn. Elke lijn die loodrecht staat op een andere lijn heeft een helling die de negatief wederkerig van de andere regel. Dit betekent dat als de helling van één lijn 2 is, de helling van een loodrechte lijn -1/2 is.
3 Gebruik de negatieve reciprook van de helling van de loodlijn. Elke lijn die loodrecht staat op een andere lijn heeft een helling die de negatief wederkerig van de andere regel. Dit betekent dat als de helling van één lijn 2 is, de helling van een loodrechte lijn -1/2 is. - Je hoeft maar twee dingen tegen de helling te doen om het negatieve omgekeerde te krijgen.
- Klap eerst het bord om. Als de helling negatief is, maak deze dan positief. Als het positief is, maak het dan negatief.
- Ten tweede, draai de teller en noemer van het getal. Dit betekent alleen dat de cijfers boven en onder van het breukvorm van plaats wisselen. Als de helling nog niet in fractievorm is, zet je het getal eenvoudig over 1 - elk geheel getal wordt alleen zelf gedeeld door 1.
- Als uw helling in decimaal is, wijzigt u deze in fractievorm voordat u deze flipt.
- De negatieve wederkerige die je net hebt gemaakt, is de helling van de andere lijn!
- De negatieve reciproque van 4 is -1/4. De negatieve reciproke van -3/2 is 2/3. De negatieve reciproke waarde van 1/8 is -8.
Methode drie van vier:
Eindig met de Point-Slope-formule
-
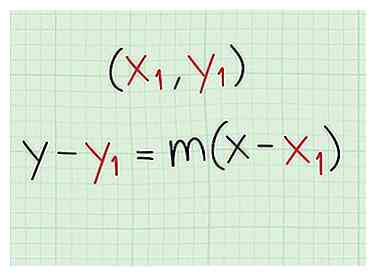 1 Gebruik de punthellingsformule om de vergelijking te vinden. Ongeacht hoe je hier bent gekomen, je zou 1 punt op de lijn en de helling van de lijn moeten hebben. De formule die moet worden gebruikt is y - y1 = m (x - x1). Gebruik de helling m je hebt zojuist berekend en een van de gegeven coördinaten op de regel, steek de nummers in de vergelijking.
1 Gebruik de punthellingsformule om de vergelijking te vinden. Ongeacht hoe je hier bent gekomen, je zou 1 punt op de lijn en de helling van de lijn moeten hebben. De formule die moet worden gebruikt is y - y1 = m (x - x1). Gebruik de helling m je hebt zojuist berekend en een van de gegeven coördinaten op de regel, steek de nummers in de vergelijking. - De X en Y zonder subscripts blijven zoals X en Y. U hoeft niets voor hen in de plaats te stellen.
- U kunt een van de gegeven punten gebruiken, als u er twee had, om te vervangen X1 en Y1. De vergelijking werkt voor elk punt op de lijn!
-
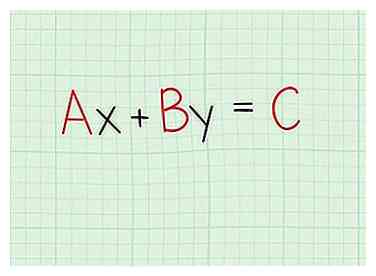 2 Verklein om te formatteren in het definitieve antwoord. Sommige leraren zijn op zoek naar standaard vorm welke is Ax + By = C, waar EEN, B, en C zijn aantal coëfficiënten. Anderen zullen willen helling-onderscheppen vorm welke is y = mx + b waar m is de helling en b is de y-intercept (waar de lijn de y-as kruist).
2 Verklein om te formatteren in het definitieve antwoord. Sommige leraren zijn op zoek naar standaard vorm welke is Ax + By = C, waar EEN, B, en C zijn aantal coëfficiënten. Anderen zullen willen helling-onderscheppen vorm welke is y = mx + b waar m is de helling en b is de y-intercept (waar de lijn de y-as kruist). - Voor beide vormen moet je alleen algebra gebruiken en de X en Y variabelen naar de juiste kanten van het gelijkteken.
- In helling-onderscheppen vorm, b zal zichzelf uitwerken als het nummer dat niet is bijgevoegd (vermenigvuldigd) met X of Y. Het is niet iets anders dat je hier moet oplossen!
Methode vier van vier:
Omgaan met onregelmatige hellingen
-
 1 Neem een helling van 0 als een goed teken. Als je op enig moment hebt ontdekt dat de helling 0 is, is je lijn horizontaal vlak! De vergelijking voor elke regel met een helling is eenvoudig y = b waar b is waar de lijn de Y-as.
1 Neem een helling van 0 als een goed teken. Als je op enig moment hebt ontdekt dat de helling 0 is, is je lijn horizontaal vlak! De vergelijking voor elke regel met een helling is eenvoudig y = b waar b is waar de lijn de Y-as. - Je kunt nog steeds door de vergelijkingen werken met m = 0, maar je zult merken dat het zich zal vermenigvuldigen X door de 0 en reduceer je vergelijking drastisch.
-
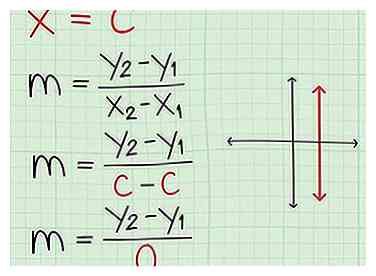 2 Leg uit dat de lijn anders verticaal is. Verticale lijnen zijn in wezen het tegenovergestelde geval. De vergelijking zal eenvoudig zijn x = c waar c is de x-as. Wanneer een regel echter recht omhoog gaat, heeft deze een onbepaald helling. Dit komt omdat wanneer je het oplost m Als u 2 punten van deze lijnen gebruikt, wordt u uiteindelijk door 0 gedeeld.
2 Leg uit dat de lijn anders verticaal is. Verticale lijnen zijn in wezen het tegenovergestelde geval. De vergelijking zal eenvoudig zijn x = c waar c is de x-as. Wanneer een regel echter recht omhoog gaat, heeft deze een onbepaald helling. Dit komt omdat wanneer je het oplost m Als u 2 punten van deze lijnen gebruikt, wordt u uiteindelijk door 0 gedeeld. - Neem de grens x = 4. De waarde van elk punt op de lijn is (4, y). Dus om op te lossen m gebruik makend van m = (y2 - y1) / (x2 - x1)zouden we krijgen m = (y2 - y1) / (4 - 4). Ongeacht wat de twee y-waarden zijn, deelt u altijd met 0.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
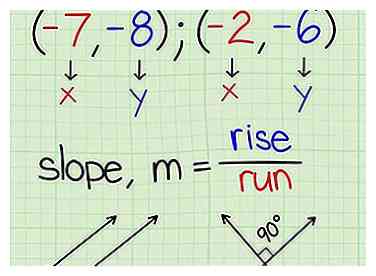 1 Kijk of je 2 punten of 1 punt en de helling krijgt. Als je 1 punt op de lijn en zijn helling krijgt, kun je doorgaan naar de Eindig met de Point-Slope-formule methode. Anders moet u de twee gegeven punten gebruiken om de helling van de lijn te vinden.
1 Kijk of je 2 punten of 1 punt en de helling krijgt. Als je 1 punt op de lijn en zijn helling krijgt, kun je doorgaan naar de Eindig met de Point-Slope-formule methode. Anders moet u de twee gegeven punten gebruiken om de helling van de lijn te vinden.  2 Gebruik andere informatie om punten op de lijn te krijgen. Sommige problemen vereisen interpretatie van informatie over de lijn om een punt op de lijn te krijgen. Als u bijvoorbeeld wordt verteld dat de lijn door de lijn loopt oorsprong, dat weet je (0, 0) is een punt op de lijn!
2 Gebruik andere informatie om punten op de lijn te krijgen. Sommige problemen vereisen interpretatie van informatie over de lijn om een punt op de lijn te krijgen. Als u bijvoorbeeld wordt verteld dat de lijn door de lijn loopt oorsprong, dat weet je (0, 0) is een punt op de lijn! 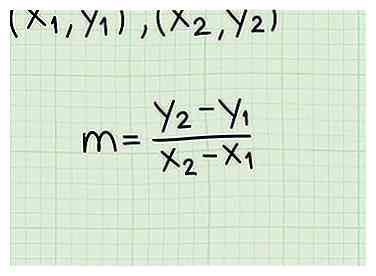 3 Bereken de helling van de lijn door de twee punten. De vergelijking voor de helling is m = (y2 - y1) / (x2 - x1). Door simpelweg uw coördinaatpunten in te pluggen en op te lossen, kent u nu de helling van de vergelijking.
3 Bereken de helling van de lijn door de twee punten. De vergelijking voor de helling is m = (y2 - y1) / (x2 - x1). Door simpelweg uw coördinaatpunten in te pluggen en op te lossen, kent u nu de helling van de vergelijking. 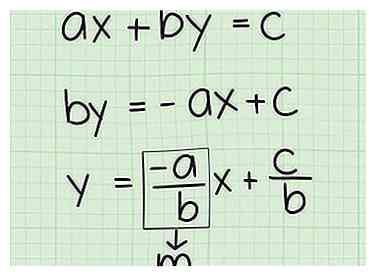 1 Gebruik dezelfde helling als de andere lijn evenwijdig is. Parallelle lijnen delen dezelfde helling, dus alles wat u hoeft te doen is de vergelijking uit die lijn gebruiken om de helling voor uw eerste lijn te krijgen.
1 Gebruik dezelfde helling als de andere lijn evenwijdig is. Parallelle lijnen delen dezelfde helling, dus alles wat u hoeft te doen is de vergelijking uit die lijn gebruiken om de helling voor uw eerste lijn te krijgen. 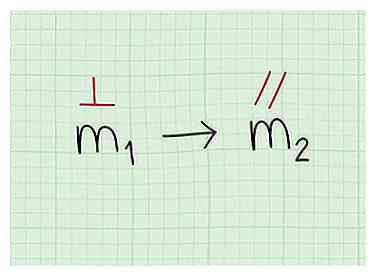 2 Zoek de helling van een loodlijn. Vaak zullen vragen je een loodrecht regel naar de regel waarvoor u een vergelijking wilt. Hier gebruikt u dezelfde concepten als eerder om de helling van de loodlijn te bepalen.
2 Zoek de helling van een loodlijn. Vaak zullen vragen je een loodrecht regel naar de regel waarvoor u een vergelijking wilt. Hier gebruikt u dezelfde concepten als eerder om de helling van de loodlijn te bepalen. 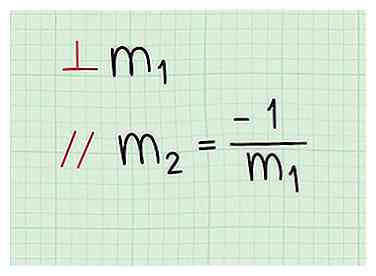 3 Gebruik de negatieve reciprook van de helling van de loodlijn. Elke lijn die loodrecht staat op een andere lijn heeft een helling die de negatief wederkerig van de andere regel. Dit betekent dat als de helling van één lijn 2 is, de helling van een loodrechte lijn -1/2 is.
3 Gebruik de negatieve reciprook van de helling van de loodlijn. Elke lijn die loodrecht staat op een andere lijn heeft een helling die de negatief wederkerig van de andere regel. Dit betekent dat als de helling van één lijn 2 is, de helling van een loodrechte lijn -1/2 is. 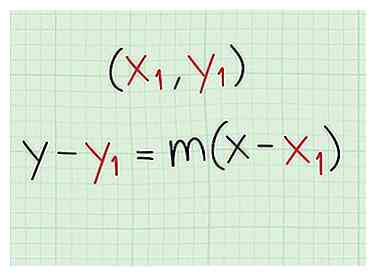 1 Gebruik de punthellingsformule om de vergelijking te vinden. Ongeacht hoe je hier bent gekomen, je zou 1 punt op de lijn en de helling van de lijn moeten hebben. De formule die moet worden gebruikt is y - y1 = m (x - x1). Gebruik de helling m je hebt zojuist berekend en een van de gegeven coördinaten op de regel, steek de nummers in de vergelijking.
1 Gebruik de punthellingsformule om de vergelijking te vinden. Ongeacht hoe je hier bent gekomen, je zou 1 punt op de lijn en de helling van de lijn moeten hebben. De formule die moet worden gebruikt is y - y1 = m (x - x1). Gebruik de helling m je hebt zojuist berekend en een van de gegeven coördinaten op de regel, steek de nummers in de vergelijking. 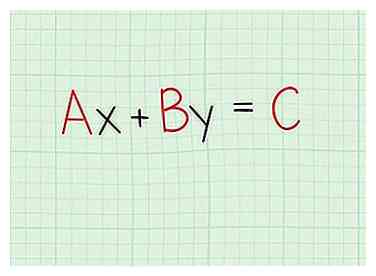 2 Verklein om te formatteren in het definitieve antwoord. Sommige leraren zijn op zoek naar standaard vorm welke is Ax + By = C, waar EEN, B, en C zijn aantal coëfficiënten. Anderen zullen willen helling-onderscheppen vorm welke is y = mx + b waar m is de helling en b is de y-intercept (waar de lijn de y-as kruist).
2 Verklein om te formatteren in het definitieve antwoord. Sommige leraren zijn op zoek naar standaard vorm welke is Ax + By = C, waar EEN, B, en C zijn aantal coëfficiënten. Anderen zullen willen helling-onderscheppen vorm welke is y = mx + b waar m is de helling en b is de y-intercept (waar de lijn de y-as kruist).  1 Neem een helling van 0 als een goed teken. Als je op enig moment hebt ontdekt dat de helling 0 is, is je lijn horizontaal vlak! De vergelijking voor elke regel met een helling is eenvoudig y = b waar b is waar de lijn de Y-as.
1 Neem een helling van 0 als een goed teken. Als je op enig moment hebt ontdekt dat de helling 0 is, is je lijn horizontaal vlak! De vergelijking voor elke regel met een helling is eenvoudig y = b waar b is waar de lijn de Y-as. 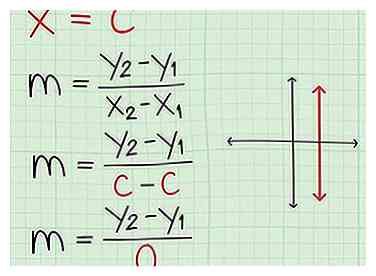 2 Leg uit dat de lijn anders verticaal is. Verticale lijnen zijn in wezen het tegenovergestelde geval. De vergelijking zal eenvoudig zijn x = c waar c is de x-as. Wanneer een regel echter recht omhoog gaat, heeft deze een onbepaald helling. Dit komt omdat wanneer je het oplost m Als u 2 punten van deze lijnen gebruikt, wordt u uiteindelijk door 0 gedeeld.
2 Leg uit dat de lijn anders verticaal is. Verticale lijnen zijn in wezen het tegenovergestelde geval. De vergelijking zal eenvoudig zijn x = c waar c is de x-as. Wanneer een regel echter recht omhoog gaat, heeft deze een onbepaald helling. Dit komt omdat wanneer je het oplost m Als u 2 punten van deze lijnen gebruikt, wordt u uiteindelijk door 0 gedeeld.