Alle juiste driehoeken hebben één rechterhoek (90 graden) en de hypotenusa is de zijde die tegenover of de rechte hoek is, of de langste zijde van de rechthoekige driehoek.[1] De hypotenusa is de langste zijde van de driehoek en is ook heel gemakkelijk te vinden op een aantal verschillende manieren. Dit artikel zal je leren hoe je de lengte van de hypotenusa kunt vinden met behulp van de stelling van Pythagoras als je de lengte van de andere twee zijden van de driehoek kent. Het zal je dan leren om de hypotenusa te herkennen van sommige speciale rechthoekige driehoeken die vaak op tests verschijnen. Het zal je uiteindelijk leren om de lengte van de hypotenusa te vinden met behulp van de Wet van Sines als je alleen de lengte van één kant kent en de maat van één extra hoek.
Methode één van de drie:
De stelling van Pythagoras gebruiken
-
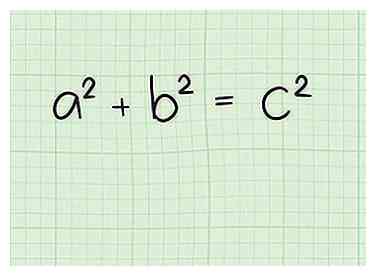 1 Leer de stelling van Pythagoras. De stelling van Pythagoras beschrijft de relatie tussen de zijden van een rechthoekige driehoek.[2] Het stelt dat voor elke rechthoekige driehoek met zijden van lengte a en b en hypotenusa van lengte c, een2 + b2 = c2.[3]
1 Leer de stelling van Pythagoras. De stelling van Pythagoras beschrijft de relatie tussen de zijden van een rechthoekige driehoek.[2] Het stelt dat voor elke rechthoekige driehoek met zijden van lengte a en b en hypotenusa van lengte c, een2 + b2 = c2.[3] -
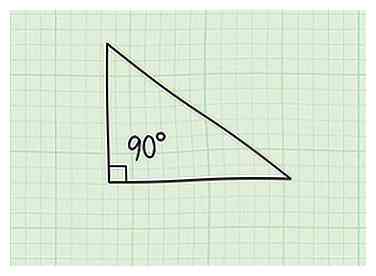 2 Zorg ervoor dat uw driehoek een rechthoekige driehoek is. De stelling van Pythagoras werkt alleen op rechte driehoeken en per definitie kunnen alleen rechte driehoeken een hypotenusa hebben. Als uw driehoek één hoek bevat die precies 90 graden is, is het een rechthoekige driehoek en kunt u doorgaan.
2 Zorg ervoor dat uw driehoek een rechthoekige driehoek is. De stelling van Pythagoras werkt alleen op rechte driehoeken en per definitie kunnen alleen rechte driehoeken een hypotenusa hebben. Als uw driehoek één hoek bevat die precies 90 graden is, is het een rechthoekige driehoek en kunt u doorgaan. - Rechte hoeken worden vaak genoteerd in tekstboeken en op tests met een klein vierkantje in de hoek van de hoek. Dit speciale teken betekent "90 graden".
-
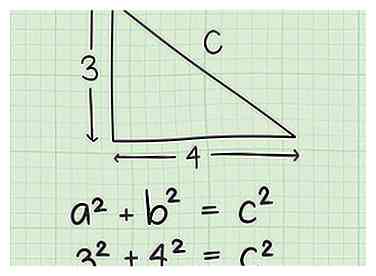 3 Wijs variabelen a, b en c toe aan de zijkanten van uw driehoek. De variabele "c" zal altijd worden toegewezen aan de hypotenusa, of de langste zijde. Kies een van de andere kanten om te zijn een, en bel de andere kant b (het maakt niet uit wat is wat, de wiskunde zal hetzelfde blijken). Kopieer vervolgens de lengtes van a en b in de formule, volgens het volgende voorbeeld:
3 Wijs variabelen a, b en c toe aan de zijkanten van uw driehoek. De variabele "c" zal altijd worden toegewezen aan de hypotenusa, of de langste zijde. Kies een van de andere kanten om te zijn een, en bel de andere kant b (het maakt niet uit wat is wat, de wiskunde zal hetzelfde blijken). Kopieer vervolgens de lengtes van a en b in de formule, volgens het volgende voorbeeld: - Als je driehoek zijden van 3 en 4 heeft en je hebt letters aan die zijden toegewezen, zodat a = 3 en b = 4, dan zou je je vergelijking moeten schrijven als: 32 + 42 = c2.
-
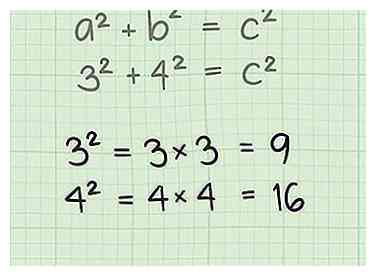 4 Zoek de vierkanten van a en b. Om het kwadraat van een getal te vinden, vermenigvuldig je eenvoudig het getal zelf, dus een2 = a x a. Zoek de vierkanten van zowel a als b en noteer ze in je formule.
4 Zoek de vierkanten van a en b. Om het kwadraat van een getal te vinden, vermenigvuldig je eenvoudig het getal zelf, dus een2 = a x a. Zoek de vierkanten van zowel a als b en noteer ze in je formule. - Als a = 3, a2 = 3 x 3, of 9. Als b = 4, dan b2 = 4 x 4 of 16.
- Wanneer u deze waarden in uw vergelijking steekt, zou het er nu als volgt uit moeten zien: 9 + 16 = c2.
-
 5 Voeg de waarden van toe een2 en b2. Voer dit in uw vergelijking in, en dit geeft u de waarde voor c2. Er is nog maar één stap te gaan en je zult die hypotenusa opgelost hebben!
5 Voeg de waarden van toe een2 en b2. Voer dit in uw vergelijking in, en dit geeft u de waarde voor c2. Er is nog maar één stap te gaan en je zult die hypotenusa opgelost hebben! - In ons voorbeeld 9 + 16 = 25, dus je moet opschrijven 25 = c2.
-
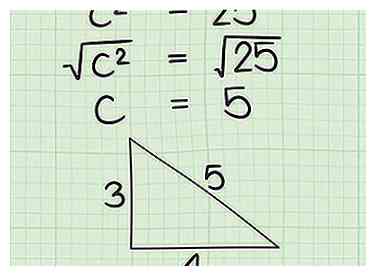 6 Zoek de vierkantswortel van c2. Gebruik de vierkantswortelfunctie op uw rekenmachine (of uw geheugen van de tafel van vermenigvuldiging) om de vierkantswortel van c te vinden2. Het antwoord is de lengte van uw hypotenusa!
6 Zoek de vierkantswortel van c2. Gebruik de vierkantswortelfunctie op uw rekenmachine (of uw geheugen van de tafel van vermenigvuldiging) om de vierkantswortel van c te vinden2. Het antwoord is de lengte van uw hypotenusa! - In ons voorbeeld c2 = 25. De vierkantswortel van 25 is 5 (5 x 5 = 25, dus Sqrt (25) = 5). Dat betekent c = 5, de lengte van onze hypotenusa!
Methode twee van drie:
De schuine zijde van driehoeken met speciale rechten vinden
-
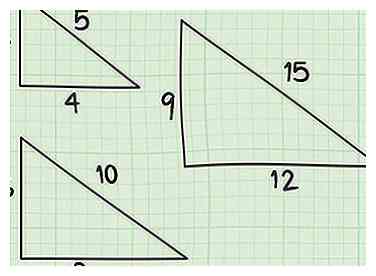 1 Leer om Pythagorean Triple Triangles te herkennen. De zijlengtes van een Pythagorean-drievoud zijn gehele getallen die passen bij de stelling van Pythagoras. Deze speciale driehoeken verschijnen vaak in meetkundehandboeken en op gestandaardiseerde tests zoals de SAT en de GRE. Als je met name de eerste 2 Pythagorean-triples onthoudt, kun je jezelf veel tijd besparen met deze tests, omdat je meteen de hypotenusa van een van deze driehoeken kunt zien door alleen naar de lengtes te kijken! [4]
1 Leer om Pythagorean Triple Triangles te herkennen. De zijlengtes van een Pythagorean-drievoud zijn gehele getallen die passen bij de stelling van Pythagoras. Deze speciale driehoeken verschijnen vaak in meetkundehandboeken en op gestandaardiseerde tests zoals de SAT en de GRE. Als je met name de eerste 2 Pythagorean-triples onthoudt, kun je jezelf veel tijd besparen met deze tests, omdat je meteen de hypotenusa van een van deze driehoeken kunt zien door alleen naar de lengtes te kijken! [4] - De eerste Pythagorean-triple is 3-4-5 (32 + 42 = 529 + 16 = 25). Als u een rechthoekige driehoek ziet met poten van lengte 3 en 4, kunt u er onmiddellijk zeker van zijn dat de hypotenusa 5 is zonder dat u berekeningen hoeft uit te voeren.
- De verhouding van een Pythagorean triple blijft kloppen, zelfs als de zijkanten worden vermenigvuldigd met een ander getal. Bijvoorbeeld een rechthoekige driehoek met benen van lengte 6 en 8 zal een hypotenusa hebben van 10 (62 + 82 = 10236 + 64 = 100). Hetzelfde geldt voor 9-12-15en zelfs 1.5-2-2.5. Probeer de wiskunde en ontdek het zelf!
- De tweede Pythagorean-triple die gewoonlijk op tests voorkomt, is 5-12-13 (52 + 122 = 13225 + 144 = 169). Wees ook op zoek naar multiples zoals 10-24-26 en 2.5-6-6.5.
-
 2 Onthoud de zijverhoudingen van een 45-45-90 rechthoekige driehoek. Een 45-45-90 rechthoekige driehoek heeft hoeken van 45, 45 en 90 graden en wordt ook een gelijkbenige rechthoekige driehoek genoemd. Het komt vaak voor bij gestandaardiseerde tests en is een heel eenvoudige driehoek om op te lossen. De verhouding tussen de zijden van deze driehoek is 1: 1: Sqrt (2), wat betekent dat de lengte van de benen gelijk is, en de lengte van de hypotenusa is gewoon de beenlengte vermenigvuldigd met de vierkantswortel van twee.
2 Onthoud de zijverhoudingen van een 45-45-90 rechthoekige driehoek. Een 45-45-90 rechthoekige driehoek heeft hoeken van 45, 45 en 90 graden en wordt ook een gelijkbenige rechthoekige driehoek genoemd. Het komt vaak voor bij gestandaardiseerde tests en is een heel eenvoudige driehoek om op te lossen. De verhouding tussen de zijden van deze driehoek is 1: 1: Sqrt (2), wat betekent dat de lengte van de benen gelijk is, en de lengte van de hypotenusa is gewoon de beenlengte vermenigvuldigd met de vierkantswortel van twee. - Om de hypotenusa van deze driehoek te berekenen op basis van de lengte van een van de benen, vermenigvuldigt u simpelweg de beenlengte met Sqrt (2).[5]
- Het kennen van deze ratio komt vooral van pas wanneer uw test- of huiswerkvraag u de nevenlengten geeft in termen van variabelen in plaats van gehele getallen.
-
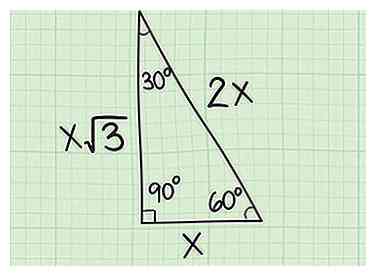 3 Leer de zijverhoudingen van een rechthoekige driehoek van 30-60-90. Deze driehoek heeft hoekmetingen van 30, 60 en 90 graden en treedt op wanneer u een gelijkzijdige driehoek doormidden snijdt. De zijden van de rechthoekige 30-60-90-rechthoek behouden altijd de verhouding 1: Sqrt (3): 2of x: Sqrt (3) x: 2x. Als u de lengte van één poot van de rechterdriehoek 30-60-90 wordt gegeven en wordt gevraagd om de schuine zijde te vinden, is dit zeer eenvoudig te doen:[6]
3 Leer de zijverhoudingen van een rechthoekige driehoek van 30-60-90. Deze driehoek heeft hoekmetingen van 30, 60 en 90 graden en treedt op wanneer u een gelijkzijdige driehoek doormidden snijdt. De zijden van de rechthoekige 30-60-90-rechthoek behouden altijd de verhouding 1: Sqrt (3): 2of x: Sqrt (3) x: 2x. Als u de lengte van één poot van de rechterdriehoek 30-60-90 wordt gegeven en wordt gevraagd om de schuine zijde te vinden, is dit zeer eenvoudig te doen:[6] - Als je de lengte van het kortste been krijgt (tegenover de hoek van 30 graden), vermenigvuldig dan de beenlengte met 2 om de lengte van de hypotenusa te vinden. Bijvoorbeeld als de lengte van de kortste poot is 4, je weet dat de hypotenusa lengte moet zijn 8.
- Als je de lengte van het langere been krijgt (tegenover de hoek van 60 graden), vermenigvuldig die lengte met 2 / wortel (3) om de lengte van de hypotenusa te vinden. Bijvoorbeeld als de lengte van het langere been is 4, je weet dat de hypotenusa lengte moet zijn 4.62.
Methode drie van drie:
De scheenachtigheid vinden met behulp van de wet van Sines
-
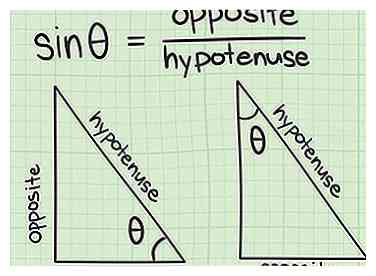 1 Begrijpen wat 'Sine' betekent. De termen "sinus," "cosinus" en "tangens" verwijzen allemaal naar verschillende verhoudingen tussen de hoeken en / of zijden van een rechthoekige driehoek. In een rechthoekige driehoek, de sinus van een hoek is gedefinieerd als de lengte van de zijde tegenover de hoek gedeeld door de hypotenusa van de driehoek. De afkorting voor sine in vergelijkingen en op rekenmachines is zonde.[7]
1 Begrijpen wat 'Sine' betekent. De termen "sinus," "cosinus" en "tangens" verwijzen allemaal naar verschillende verhoudingen tussen de hoeken en / of zijden van een rechthoekige driehoek. In een rechthoekige driehoek, de sinus van een hoek is gedefinieerd als de lengte van de zijde tegenover de hoek gedeeld door de hypotenusa van de driehoek. De afkorting voor sine in vergelijkingen en op rekenmachines is zonde.[7] -
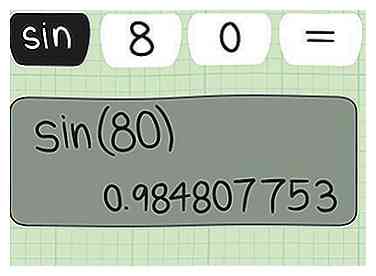 2 Leer om sinus te berekenen. Zelfs een eenvoudige wetenschappelijke rekenmachine heeft een sinusfunctie. Zoek naar een sleutel gemarkeerd zonde. Om de sinus van de hoek te vinden, drukt u meestal op de zonde toets en voer vervolgens de hoekmeting in graden in. Op sommige rekenmachines moet u echter eerst de graadmeting invoeren en vervolgens de zonde sleutel. Je zult met je rekenmachine moeten experimenteren of de handleiding moeten checken om erachter te komen welke het is.
2 Leer om sinus te berekenen. Zelfs een eenvoudige wetenschappelijke rekenmachine heeft een sinusfunctie. Zoek naar een sleutel gemarkeerd zonde. Om de sinus van de hoek te vinden, drukt u meestal op de zonde toets en voer vervolgens de hoekmeting in graden in. Op sommige rekenmachines moet u echter eerst de graadmeting invoeren en vervolgens de zonde sleutel. Je zult met je rekenmachine moeten experimenteren of de handleiding moeten checken om erachter te komen welke het is. - Om de sinus van een hoek van 80 graden te vinden, moet je ofwel intoetsen zonde 80 gevolgd door het gelijkteken of de Enter-toets, of 80 zonde. (Het antwoord is -0.9939.)
- U kunt ook 'sine calculator' in een zoekopdracht op internet typen en een aantal gebruiksvriendelijke rekenmachines vinden die elk giswerk zullen verwijderen.[8]
-
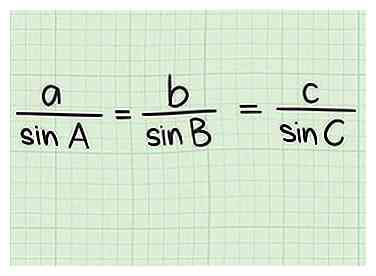 3 Leer de wet van Sines. De wet van Sines is een handig hulpmiddel voor het oplossen van driehoeken. In het bijzonder kan het u helpen de hypotenusa van een rechthoekige driehoek te vinden als u de lengte van één kant kent en de maat van een andere hoek naast de rechte hoek. Voor elke driehoek met zijden een, b, en cen hoeken EEN, B, en C, de wet van Sines stelt dat een / zonde EEN = b / zonde B = c / zonde C.[9]
3 Leer de wet van Sines. De wet van Sines is een handig hulpmiddel voor het oplossen van driehoeken. In het bijzonder kan het u helpen de hypotenusa van een rechthoekige driehoek te vinden als u de lengte van één kant kent en de maat van een andere hoek naast de rechte hoek. Voor elke driehoek met zijden een, b, en cen hoeken EEN, B, en C, de wet van Sines stelt dat een / zonde EEN = b / zonde B = c / zonde C.[9] - De Wet van Sines kan eigenlijk worden gebruikt om op te lossen ieder driehoek, maar alleen een rechthoekige driehoek heeft een hypotenusa.
-
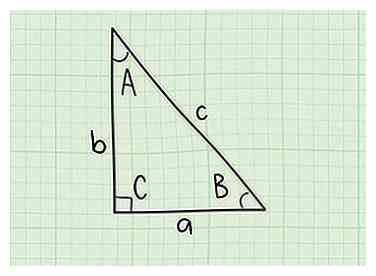 4 Ken de variabelen a, b en c toe aan de zijkanten van uw driehoek. De hypotenusa (langste zijde) moet "c" zijn. Schrijf ter wille van de eenvoud de kant met de bekende lengte als "a" en de andere "b". Wijs de variabelen A, B en C vervolgens toe aan de hoeken van de driehoek. De rechte hoek tegenover de hypotenusa is "C". De hoek tegenoverliggende zijde "a" is hoek "A" en de hoek tegenoverliggende zijde "b" is "B".
4 Ken de variabelen a, b en c toe aan de zijkanten van uw driehoek. De hypotenusa (langste zijde) moet "c" zijn. Schrijf ter wille van de eenvoud de kant met de bekende lengte als "a" en de andere "b". Wijs de variabelen A, B en C vervolgens toe aan de hoeken van de driehoek. De rechte hoek tegenover de hypotenusa is "C". De hoek tegenoverliggende zijde "a" is hoek "A" en de hoek tegenoverliggende zijde "b" is "B". -
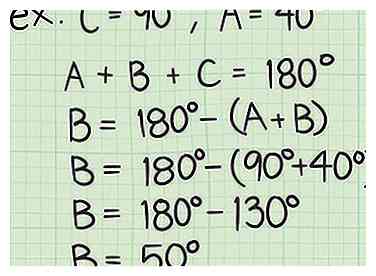 5 Bereken de meting van de derde hoek. Omdat het een rechte hoek is, weet je dat al C = 90 graden, en je weet ook de maat van EEN of B. Aangezien de interne graadmeting van een driehoek altijd gelijk moet zijn aan 180 graden, kunt u eenvoudig de meting van de derde hoek berekenen met behulp van de volgende formule: 180 - (90 + A) = B. Je kunt de vergelijking ook zo omdraaien 180 - (90 + B) = A.
5 Bereken de meting van de derde hoek. Omdat het een rechte hoek is, weet je dat al C = 90 graden, en je weet ook de maat van EEN of B. Aangezien de interne graadmeting van een driehoek altijd gelijk moet zijn aan 180 graden, kunt u eenvoudig de meting van de derde hoek berekenen met behulp van de volgende formule: 180 - (90 + A) = B. Je kunt de vergelijking ook zo omdraaien 180 - (90 + B) = A. - Bijvoorbeeld, als u dat weet A = 40 graden, dan B = 180 - (90 + 40). Vereenvoudig dit om B = 180 - 130en dat kun je snel bepalen B = 50 graden.
-
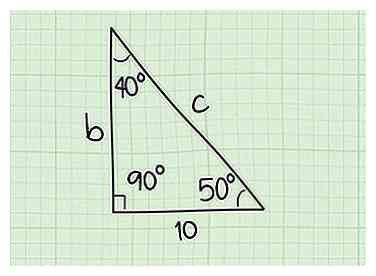 6 Onderzoek uw driehoek. Op dit moment moet u de graadmetingen van alle drie de hoeken kennen, en de lengte van zijde a. Het is nu tijd om deze informatie in de Law of Sines-vergelijking te pluggen om de lengte van de andere twee zijden te bepalen.
6 Onderzoek uw driehoek. Op dit moment moet u de graadmetingen van alle drie de hoeken kennen, en de lengte van zijde a. Het is nu tijd om deze informatie in de Law of Sines-vergelijking te pluggen om de lengte van de andere twee zijden te bepalen. - Als u wilt doorgaan met ons voorbeeld, stellen we dat de lengte van zijde a = 10. Hoek C = 90 graden, hoek A = 40 graden en hoek B = 50 graden.
-
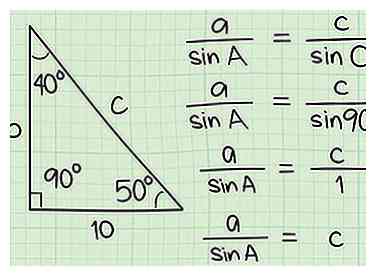 7 Pas de wet van Sines toe op je driehoek. We hoeven alleen maar onze nummers in te pluggen en de volgende vergelijking op te lossen om de lengte van hypotenusa c te bepalen: lengte van zijde a / zonde A = lengte van zijde c / zonde C. Dit ziet er misschien nog een beetje intimiderend uit, maar de sinus van 90 graden is een constante en is altijd gelijk aan 1! Onze vergelijking kan dus worden vereenvoudigd om: een / zonde A = c / 1, of gewoon een / zonde A = c.
7 Pas de wet van Sines toe op je driehoek. We hoeven alleen maar onze nummers in te pluggen en de volgende vergelijking op te lossen om de lengte van hypotenusa c te bepalen: lengte van zijde a / zonde A = lengte van zijde c / zonde C. Dit ziet er misschien nog een beetje intimiderend uit, maar de sinus van 90 graden is een constante en is altijd gelijk aan 1! Onze vergelijking kan dus worden vereenvoudigd om: een / zonde A = c / 1, of gewoon een / zonde A = c. -
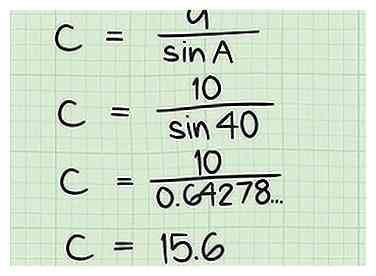 8 Verdeel de lengte van de zijkant een door de sinus van hoek EEN om de lengte van de hypotenusa te vinden! U kunt dit in twee afzonderlijke stappen doen, door eerst te berekenen zonde A en het opschrijven en vervolgens delen door een. Of u kunt het tegelijkertijd in de rekenmachine intoetsen. Als dat zo is, vergeet dan niet om haakjes op te nemen na het deelteken. Typ bijvoorbeeld een van beide 10 / (zonde 40) of 10 / (40 zonde), afhankelijk van uw rekenmachine.
8 Verdeel de lengte van de zijkant een door de sinus van hoek EEN om de lengte van de hypotenusa te vinden! U kunt dit in twee afzonderlijke stappen doen, door eerst te berekenen zonde A en het opschrijven en vervolgens delen door een. Of u kunt het tegelijkertijd in de rekenmachine intoetsen. Als dat zo is, vergeet dan niet om haakjes op te nemen na het deelteken. Typ bijvoorbeeld een van beide 10 / (zonde 40) of 10 / (40 zonde), afhankelijk van uw rekenmachine. - Met behulp van ons voorbeeld vinden we dat zonde 40 = 0,64278761. Om de waarde van c te vinden, delen we eenvoudig de lengte van een door dit getal en leren dat 10 / 0.64278761 = 15.6, de lengte van onze hypotenusa!
 Minotauromaquia
Minotauromaquia
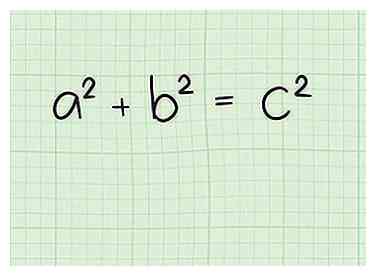 1 Leer de stelling van Pythagoras. De stelling van Pythagoras beschrijft de relatie tussen de zijden van een rechthoekige driehoek.[2] Het stelt dat voor elke rechthoekige driehoek met zijden van lengte a en b en hypotenusa van lengte c, een2 + b2 = c2.[3]
1 Leer de stelling van Pythagoras. De stelling van Pythagoras beschrijft de relatie tussen de zijden van een rechthoekige driehoek.[2] Het stelt dat voor elke rechthoekige driehoek met zijden van lengte a en b en hypotenusa van lengte c, een2 + b2 = c2.[3]  2 Zorg ervoor dat uw driehoek een rechthoekige driehoek is. De stelling van Pythagoras werkt alleen op rechte driehoeken en per definitie kunnen alleen rechte driehoeken een hypotenusa hebben. Als uw driehoek één hoek bevat die precies 90 graden is, is het een rechthoekige driehoek en kunt u doorgaan.
2 Zorg ervoor dat uw driehoek een rechthoekige driehoek is. De stelling van Pythagoras werkt alleen op rechte driehoeken en per definitie kunnen alleen rechte driehoeken een hypotenusa hebben. Als uw driehoek één hoek bevat die precies 90 graden is, is het een rechthoekige driehoek en kunt u doorgaan.  3 Wijs variabelen a, b en c toe aan de zijkanten van uw driehoek. De variabele "c" zal altijd worden toegewezen aan de hypotenusa, of de langste zijde. Kies een van de andere kanten om te zijn een, en bel de andere kant b (het maakt niet uit wat is wat, de wiskunde zal hetzelfde blijken). Kopieer vervolgens de lengtes van a en b in de formule, volgens het volgende voorbeeld:
3 Wijs variabelen a, b en c toe aan de zijkanten van uw driehoek. De variabele "c" zal altijd worden toegewezen aan de hypotenusa, of de langste zijde. Kies een van de andere kanten om te zijn een, en bel de andere kant b (het maakt niet uit wat is wat, de wiskunde zal hetzelfde blijken). Kopieer vervolgens de lengtes van a en b in de formule, volgens het volgende voorbeeld: 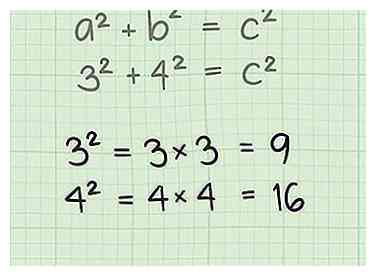 4 Zoek de vierkanten van a en b. Om het kwadraat van een getal te vinden, vermenigvuldig je eenvoudig het getal zelf, dus een2 = a x a. Zoek de vierkanten van zowel a als b en noteer ze in je formule.
4 Zoek de vierkanten van a en b. Om het kwadraat van een getal te vinden, vermenigvuldig je eenvoudig het getal zelf, dus een2 = a x a. Zoek de vierkanten van zowel a als b en noteer ze in je formule.  5 Voeg de waarden van toe een2 en b2. Voer dit in uw vergelijking in, en dit geeft u de waarde voor c2. Er is nog maar één stap te gaan en je zult die hypotenusa opgelost hebben!
5 Voeg de waarden van toe een2 en b2. Voer dit in uw vergelijking in, en dit geeft u de waarde voor c2. Er is nog maar één stap te gaan en je zult die hypotenusa opgelost hebben! 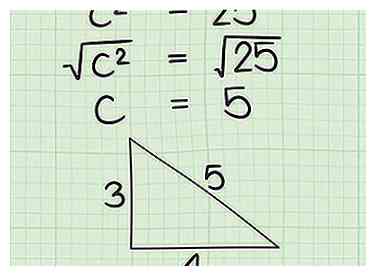 6 Zoek de vierkantswortel van c2. Gebruik de vierkantswortelfunctie op uw rekenmachine (of uw geheugen van de tafel van vermenigvuldiging) om de vierkantswortel van c te vinden2. Het antwoord is de lengte van uw hypotenusa!
6 Zoek de vierkantswortel van c2. Gebruik de vierkantswortelfunctie op uw rekenmachine (of uw geheugen van de tafel van vermenigvuldiging) om de vierkantswortel van c te vinden2. Het antwoord is de lengte van uw hypotenusa!  1 Leer om Pythagorean Triple Triangles te herkennen. De zijlengtes van een Pythagorean-drievoud zijn gehele getallen die passen bij de stelling van Pythagoras. Deze speciale driehoeken verschijnen vaak in meetkundehandboeken en op gestandaardiseerde tests zoals de SAT en de GRE. Als je met name de eerste 2 Pythagorean-triples onthoudt, kun je jezelf veel tijd besparen met deze tests, omdat je meteen de hypotenusa van een van deze driehoeken kunt zien door alleen naar de lengtes te kijken! [4]
1 Leer om Pythagorean Triple Triangles te herkennen. De zijlengtes van een Pythagorean-drievoud zijn gehele getallen die passen bij de stelling van Pythagoras. Deze speciale driehoeken verschijnen vaak in meetkundehandboeken en op gestandaardiseerde tests zoals de SAT en de GRE. Als je met name de eerste 2 Pythagorean-triples onthoudt, kun je jezelf veel tijd besparen met deze tests, omdat je meteen de hypotenusa van een van deze driehoeken kunt zien door alleen naar de lengtes te kijken! [4]  2 Onthoud de zijverhoudingen van een 45-45-90 rechthoekige driehoek. Een 45-45-90 rechthoekige driehoek heeft hoeken van 45, 45 en 90 graden en wordt ook een gelijkbenige rechthoekige driehoek genoemd. Het komt vaak voor bij gestandaardiseerde tests en is een heel eenvoudige driehoek om op te lossen. De verhouding tussen de zijden van deze driehoek is 1: 1: Sqrt (2), wat betekent dat de lengte van de benen gelijk is, en de lengte van de hypotenusa is gewoon de beenlengte vermenigvuldigd met de vierkantswortel van twee.
2 Onthoud de zijverhoudingen van een 45-45-90 rechthoekige driehoek. Een 45-45-90 rechthoekige driehoek heeft hoeken van 45, 45 en 90 graden en wordt ook een gelijkbenige rechthoekige driehoek genoemd. Het komt vaak voor bij gestandaardiseerde tests en is een heel eenvoudige driehoek om op te lossen. De verhouding tussen de zijden van deze driehoek is 1: 1: Sqrt (2), wat betekent dat de lengte van de benen gelijk is, en de lengte van de hypotenusa is gewoon de beenlengte vermenigvuldigd met de vierkantswortel van twee.  3 Leer de zijverhoudingen van een rechthoekige driehoek van 30-60-90. Deze driehoek heeft hoekmetingen van 30, 60 en 90 graden en treedt op wanneer u een gelijkzijdige driehoek doormidden snijdt. De zijden van de rechthoekige 30-60-90-rechthoek behouden altijd de verhouding 1: Sqrt (3): 2of x: Sqrt (3) x: 2x. Als u de lengte van één poot van de rechterdriehoek 30-60-90 wordt gegeven en wordt gevraagd om de schuine zijde te vinden, is dit zeer eenvoudig te doen:[6]
3 Leer de zijverhoudingen van een rechthoekige driehoek van 30-60-90. Deze driehoek heeft hoekmetingen van 30, 60 en 90 graden en treedt op wanneer u een gelijkzijdige driehoek doormidden snijdt. De zijden van de rechthoekige 30-60-90-rechthoek behouden altijd de verhouding 1: Sqrt (3): 2of x: Sqrt (3) x: 2x. Als u de lengte van één poot van de rechterdriehoek 30-60-90 wordt gegeven en wordt gevraagd om de schuine zijde te vinden, is dit zeer eenvoudig te doen:[6]  1 Begrijpen wat 'Sine' betekent. De termen "sinus," "cosinus" en "tangens" verwijzen allemaal naar verschillende verhoudingen tussen de hoeken en / of zijden van een rechthoekige driehoek. In een rechthoekige driehoek, de sinus van een hoek is gedefinieerd als de lengte van de zijde tegenover de hoek gedeeld door de hypotenusa van de driehoek. De afkorting voor sine in vergelijkingen en op rekenmachines is zonde.[7]
1 Begrijpen wat 'Sine' betekent. De termen "sinus," "cosinus" en "tangens" verwijzen allemaal naar verschillende verhoudingen tussen de hoeken en / of zijden van een rechthoekige driehoek. In een rechthoekige driehoek, de sinus van een hoek is gedefinieerd als de lengte van de zijde tegenover de hoek gedeeld door de hypotenusa van de driehoek. De afkorting voor sine in vergelijkingen en op rekenmachines is zonde.[7]  2 Leer om sinus te berekenen. Zelfs een eenvoudige wetenschappelijke rekenmachine heeft een sinusfunctie. Zoek naar een sleutel gemarkeerd zonde. Om de sinus van de hoek te vinden, drukt u meestal op de zonde toets en voer vervolgens de hoekmeting in graden in. Op sommige rekenmachines moet u echter eerst de graadmeting invoeren en vervolgens de zonde sleutel. Je zult met je rekenmachine moeten experimenteren of de handleiding moeten checken om erachter te komen welke het is.
2 Leer om sinus te berekenen. Zelfs een eenvoudige wetenschappelijke rekenmachine heeft een sinusfunctie. Zoek naar een sleutel gemarkeerd zonde. Om de sinus van de hoek te vinden, drukt u meestal op de zonde toets en voer vervolgens de hoekmeting in graden in. Op sommige rekenmachines moet u echter eerst de graadmeting invoeren en vervolgens de zonde sleutel. Je zult met je rekenmachine moeten experimenteren of de handleiding moeten checken om erachter te komen welke het is. 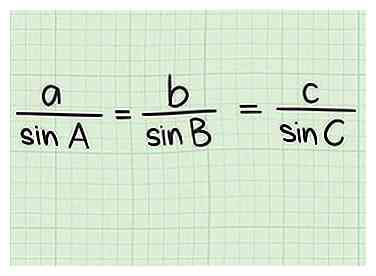 3 Leer de wet van Sines. De wet van Sines is een handig hulpmiddel voor het oplossen van driehoeken. In het bijzonder kan het u helpen de hypotenusa van een rechthoekige driehoek te vinden als u de lengte van één kant kent en de maat van een andere hoek naast de rechte hoek. Voor elke driehoek met zijden een, b, en cen hoeken EEN, B, en C, de wet van Sines stelt dat een / zonde EEN = b / zonde B = c / zonde C.[9]
3 Leer de wet van Sines. De wet van Sines is een handig hulpmiddel voor het oplossen van driehoeken. In het bijzonder kan het u helpen de hypotenusa van een rechthoekige driehoek te vinden als u de lengte van één kant kent en de maat van een andere hoek naast de rechte hoek. Voor elke driehoek met zijden een, b, en cen hoeken EEN, B, en C, de wet van Sines stelt dat een / zonde EEN = b / zonde B = c / zonde C.[9]  4 Ken de variabelen a, b en c toe aan de zijkanten van uw driehoek. De hypotenusa (langste zijde) moet "c" zijn. Schrijf ter wille van de eenvoud de kant met de bekende lengte als "a" en de andere "b". Wijs de variabelen A, B en C vervolgens toe aan de hoeken van de driehoek. De rechte hoek tegenover de hypotenusa is "C". De hoek tegenoverliggende zijde "a" is hoek "A" en de hoek tegenoverliggende zijde "b" is "B".
4 Ken de variabelen a, b en c toe aan de zijkanten van uw driehoek. De hypotenusa (langste zijde) moet "c" zijn. Schrijf ter wille van de eenvoud de kant met de bekende lengte als "a" en de andere "b". Wijs de variabelen A, B en C vervolgens toe aan de hoeken van de driehoek. De rechte hoek tegenover de hypotenusa is "C". De hoek tegenoverliggende zijde "a" is hoek "A" en de hoek tegenoverliggende zijde "b" is "B". 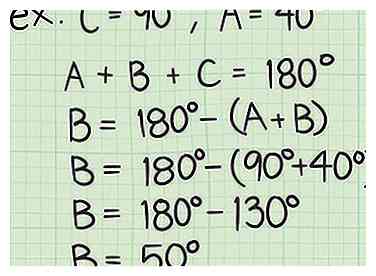 5 Bereken de meting van de derde hoek. Omdat het een rechte hoek is, weet je dat al C = 90 graden, en je weet ook de maat van EEN of B. Aangezien de interne graadmeting van een driehoek altijd gelijk moet zijn aan 180 graden, kunt u eenvoudig de meting van de derde hoek berekenen met behulp van de volgende formule: 180 - (90 + A) = B. Je kunt de vergelijking ook zo omdraaien 180 - (90 + B) = A.
5 Bereken de meting van de derde hoek. Omdat het een rechte hoek is, weet je dat al C = 90 graden, en je weet ook de maat van EEN of B. Aangezien de interne graadmeting van een driehoek altijd gelijk moet zijn aan 180 graden, kunt u eenvoudig de meting van de derde hoek berekenen met behulp van de volgende formule: 180 - (90 + A) = B. Je kunt de vergelijking ook zo omdraaien 180 - (90 + B) = A.  6 Onderzoek uw driehoek. Op dit moment moet u de graadmetingen van alle drie de hoeken kennen, en de lengte van zijde a. Het is nu tijd om deze informatie in de Law of Sines-vergelijking te pluggen om de lengte van de andere twee zijden te bepalen.
6 Onderzoek uw driehoek. Op dit moment moet u de graadmetingen van alle drie de hoeken kennen, en de lengte van zijde a. Het is nu tijd om deze informatie in de Law of Sines-vergelijking te pluggen om de lengte van de andere twee zijden te bepalen.  7 Pas de wet van Sines toe op je driehoek. We hoeven alleen maar onze nummers in te pluggen en de volgende vergelijking op te lossen om de lengte van hypotenusa c te bepalen: lengte van zijde a / zonde A = lengte van zijde c / zonde C. Dit ziet er misschien nog een beetje intimiderend uit, maar de sinus van 90 graden is een constante en is altijd gelijk aan 1! Onze vergelijking kan dus worden vereenvoudigd om: een / zonde A = c / 1, of gewoon een / zonde A = c.
7 Pas de wet van Sines toe op je driehoek. We hoeven alleen maar onze nummers in te pluggen en de volgende vergelijking op te lossen om de lengte van hypotenusa c te bepalen: lengte van zijde a / zonde A = lengte van zijde c / zonde C. Dit ziet er misschien nog een beetje intimiderend uit, maar de sinus van 90 graden is een constante en is altijd gelijk aan 1! Onze vergelijking kan dus worden vereenvoudigd om: een / zonde A = c / 1, of gewoon een / zonde A = c. 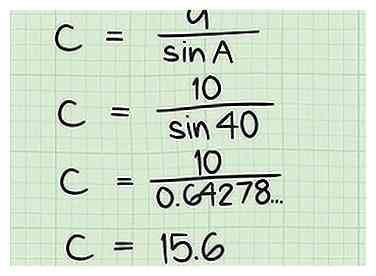 8 Verdeel de lengte van de zijkant een door de sinus van hoek EEN om de lengte van de hypotenusa te vinden! U kunt dit in twee afzonderlijke stappen doen, door eerst te berekenen zonde A en het opschrijven en vervolgens delen door een. Of u kunt het tegelijkertijd in de rekenmachine intoetsen. Als dat zo is, vergeet dan niet om haakjes op te nemen na het deelteken. Typ bijvoorbeeld een van beide 10 / (zonde 40) of 10 / (40 zonde), afhankelijk van uw rekenmachine.
8 Verdeel de lengte van de zijkant een door de sinus van hoek EEN om de lengte van de hypotenusa te vinden! U kunt dit in twee afzonderlijke stappen doen, door eerst te berekenen zonde A en het opschrijven en vervolgens delen door een. Of u kunt het tegelijkertijd in de rekenmachine intoetsen. Als dat zo is, vergeet dan niet om haakjes op te nemen na het deelteken. Typ bijvoorbeeld een van beide 10 / (zonde 40) of 10 / (40 zonde), afhankelijk van uw rekenmachine.