Een cirkel is een tweedimensionale lijn die een gesloten lus vormt, waarbij elk punt op die lus op gelijke afstand van het midden ligt.[1] De omtrek (C) van een cirkel is de omtrek of de afstand eromheen.[2] Het gebied (A) van een cirkel is hoeveel ruimte de cirkel inname of het gebied dat wordt omsloten door de cirkel.[3] Zowel het gebied als de omtrek kunnen worden berekend met eenvoudige formules met behulp van de straal of diameter van de cirkel en de waarde van pi.
Deel een van de drie:
De omtrek berekenen
-
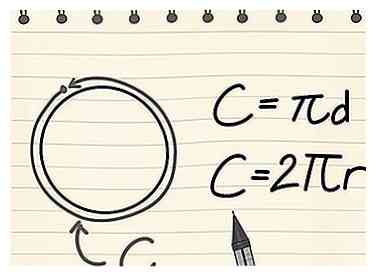 1 Leer de formule voor omtrek. Er zijn twee formules die kunnen worden gebruikt om de omtrek van een cirkel te berekenen: C = 2πr of C = πd, waarbij π de wiskundige constante is die ongeveer gelijk is aan 3,14,[4]r is gelijk aan de straal, en d is gelijk aan de diameter.[5]
1 Leer de formule voor omtrek. Er zijn twee formules die kunnen worden gebruikt om de omtrek van een cirkel te berekenen: C = 2πr of C = πd, waarbij π de wiskundige constante is die ongeveer gelijk is aan 3,14,[4]r is gelijk aan de straal, en d is gelijk aan de diameter.[5] - Omdat de straal van een cirkel gelijk is aan tweemaal de diameter, zijn deze vergelijkingen in wezen hetzelfde.
- De eenheden voor omtrek kunnen elke maateenheid zijn voor de lengte: voeten, mijlen, meters, centimeters, enz.
-
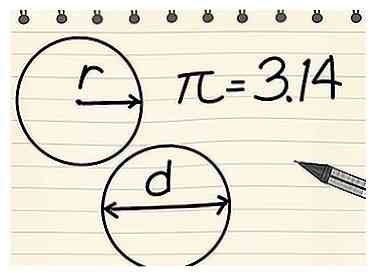 2 Begrijp de verschillende delen van de formule. Er zijn drie componenten voor het vinden van de omtrek van een cirkel: straal, diameter en π. De straal en diameter zijn gerelateerd: de straal is gelijk aan de helft van de diameter, terwijl de diameter gelijk is aan de dubbele straal.
2 Begrijp de verschillende delen van de formule. Er zijn drie componenten voor het vinden van de omtrek van een cirkel: straal, diameter en π. De straal en diameter zijn gerelateerd: de straal is gelijk aan de helft van de diameter, terwijl de diameter gelijk is aan de dubbele straal. - De straal (r) van een cirkel is de afstand van één punt op de cirkel tot het midden van de cirkel.
- De diameter (d) van een cirkel is de afstand van het ene punt op de cirkel naar het andere recht er tegenover, en gaat door het midden van de cirkel.[6]
- De Griekse letter pi (π) vertegenwoordigt de verhouding van de omtrek gedeeld door de diameter en wordt weergegeven door het getal 3.14159265 ..., een irrationeel getal dat geen laatste cijfer of een herkenbaar patroon van herhalende cijfers heeft.[7] Dit aantal wordt gewoonlijk afgerond op 3,14 voor basisberekeningen.
-
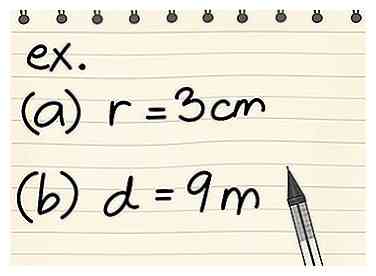 3 Meet de straal of diameter van de cirkel. Gebruik een liniaal, plaats het ene uiteinde aan een kant van de cirkel en plaats het door het middelpunt naar de andere kant van de cirkel. De afstand tot het middelpunt van de cirkel is de straal, terwijl de afstand tot het andere uiteinde van de cirkel de diameter is.
3 Meet de straal of diameter van de cirkel. Gebruik een liniaal, plaats het ene uiteinde aan een kant van de cirkel en plaats het door het middelpunt naar de andere kant van de cirkel. De afstand tot het middelpunt van de cirkel is de straal, terwijl de afstand tot het andere uiteinde van de cirkel de diameter is. - In de meeste wiskundeproblemen in het leerboek wordt de straal of diameter aan u gegeven.
-
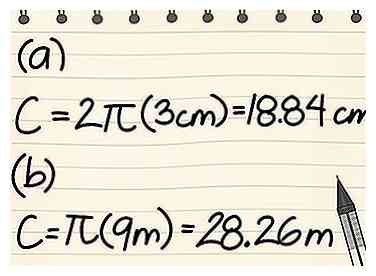 4 Sluit de variabelen aan en los het op. Nadat u de straal en / of diameter van de cirkel hebt bepaald, kunt u deze variabelen in de juiste vergelijking invoegen. Als u de straal hebt, gebruik dan C = 2πr, maar als je de diameter hebt, gebruik dan C = πd.
4 Sluit de variabelen aan en los het op. Nadat u de straal en / of diameter van de cirkel hebt bepaald, kunt u deze variabelen in de juiste vergelijking invoegen. Als u de straal hebt, gebruik dan C = 2πr, maar als je de diameter hebt, gebruik dan C = πd. - Bijvoorbeeld: Wat is de omtrek van een cirkel met een straal van 3 cm?
- Schrijf de formule: C = 2πr
- Plug de variabelen in: C = 2π3
- Vermenigvuldig door: C = (2 * 3 * π) = 6π = 18,84 cm
- Bijvoorbeeld: wat is de omtrek van een cirkel met een diameter van 9 m?
- Schrijf de formule: C = πd
- Plug de variabelen in: C = 9π
- Vermenigvuldig door: C = (9 * π) = 28,26 m
- Bijvoorbeeld: Wat is de omtrek van een cirkel met een straal van 3 cm?
-
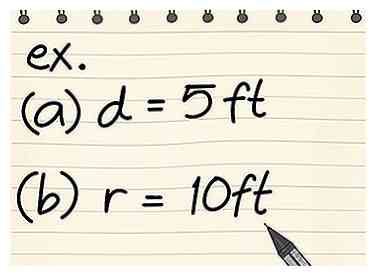 5 Oefen met een paar voorbeelden. Nu je de formule hebt geleerd, is het tijd om te oefenen met een paar voorbeelden. Hoe meer problemen u oplost, hoe gemakkelijker het wordt om ze in de toekomst op te lossen.
5 Oefen met een paar voorbeelden. Nu je de formule hebt geleerd, is het tijd om te oefenen met een paar voorbeelden. Hoe meer problemen u oplost, hoe gemakkelijker het wordt om ze in de toekomst op te lossen. - Zoek de omtrek van een cirkel met een diameter van 5 ft.
- C = πd = 5π = 15,7 meter
- Zoek de omtrek van een cirkel met een straal van 10 ft.
- C = 2πr = C = 2π10 = 2 * 10 * π = 62,8 ft.
- Zoek de omtrek van een cirkel met een diameter van 5 ft.
Tweede deel van de drie:
Het gebied berekenen
-
 1 Leer de formule voor het gebied van een cirkel. Het oppervlak van een cirkel kan worden berekend met behulp van de diameter of de straal met twee verschillende formules: A = πr2 of A = π (d / 2)2,[8] waarbij π de wiskundige constante is die ongeveer gelijk is aan 3,14,[9]r is gelijk aan de straal, en d is de diameter.
1 Leer de formule voor het gebied van een cirkel. Het oppervlak van een cirkel kan worden berekend met behulp van de diameter of de straal met twee verschillende formules: A = πr2 of A = π (d / 2)2,[8] waarbij π de wiskundige constante is die ongeveer gelijk is aan 3,14,[9]r is gelijk aan de straal, en d is de diameter. - Omdat de straal van een cirkel gelijk is aan de helft van de diameter, zijn deze vergelijkingen in wezen hetzelfde.
- De eenheden voor oppervlakte kunnen elke eenheid zijn voor de maat van de lengte in het kwadraat: vierkante voet (ft2), vierkante meters (m2), centimeter kwadraat (cm2), enz.
-
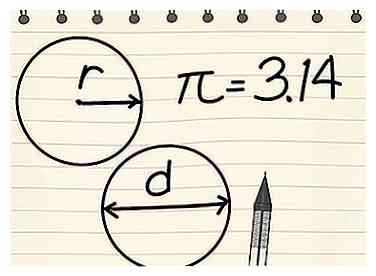 2 Begrijp de verschillende delen van de formule. Er zijn drie componenten voor het vinden van de omtrek van een cirkel: straal, diameter en π. De straal en diameter zijn gerelateerd: de straal is gelijk aan de helft van de diameter, terwijl de diameter gelijk is aan de dubbele straal.
2 Begrijp de verschillende delen van de formule. Er zijn drie componenten voor het vinden van de omtrek van een cirkel: straal, diameter en π. De straal en diameter zijn gerelateerd: de straal is gelijk aan de helft van de diameter, terwijl de diameter gelijk is aan de dubbele straal. - De straal (r) van een cirkel is de afstand van één punt op de cirkel tot het midden van de cirkel.
- De diameter (d) van een cirkel is de afstand van het ene punt op de cirkel naar het andere recht er tegenover, en gaat door het midden van de cirkel.[10]
- De Griekse letter pi (π) vertegenwoordigt de verhouding van de omtrek gedeeld door de diameter en wordt weergegeven door het getal 3.14159265 ..., een irrationeel getal dat geen laatste cijfer of een herkenbaar patroon van herhalende cijfers heeft.[11] Dit aantal wordt gewoonlijk afgerond op 3,14 voor basisberekeningen.
-
 3 Meet de straal of diameter van de cirkel. Gebruik een liniaal, plaats het ene uiteinde aan een kant van de cirkel en plaats het door het middelpunt naar de andere kant van de cirkel. De afstand tot het middelpunt van de cirkel is de straal, terwijl de afstand tot het andere uiteinde van de cirkel de diameter is.
3 Meet de straal of diameter van de cirkel. Gebruik een liniaal, plaats het ene uiteinde aan een kant van de cirkel en plaats het door het middelpunt naar de andere kant van de cirkel. De afstand tot het middelpunt van de cirkel is de straal, terwijl de afstand tot het andere uiteinde van de cirkel de diameter is. - In de meeste wiskundeproblemen in het leerboek wordt de straal of diameter aan u gegeven.
-
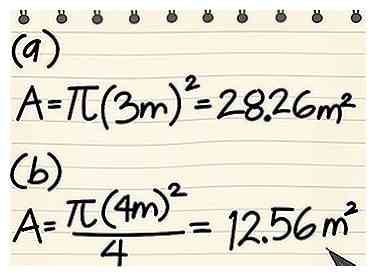 4 Sluit de variabelen aan en los het op. Nadat u de straal en / of diameter van de cirkel hebt bepaald, kunt u deze variabelen in de juiste vergelijking invoegen. Als u de straal hebt, gebruik dan A = πr2, maar als je de diameter hebt, gebruik dan A = π (d / 2)2.
4 Sluit de variabelen aan en los het op. Nadat u de straal en / of diameter van de cirkel hebt bepaald, kunt u deze variabelen in de juiste vergelijking invoegen. Als u de straal hebt, gebruik dan A = πr2, maar als je de diameter hebt, gebruik dan A = π (d / 2)2. - Bijvoorbeeld: wat is het oppervlak van een cirkel met een straal van 3 m?
- Schrijf de formule: A = πr2
- Sluit de variabelen aan: A = π32
- Vier de straal: r2 = 32 = 9
- Vermenigvuldig met pi: EEN = 9π = 28,26 m2
- Bijvoorbeeld: wat is het oppervlak van een cirkel met een diameter van 4 m?
- Schrijf de formule: A = π (d / 2)2
- Sluit de variabelen aan: A = π (4/2)2
- Verdeel de diameter door 2: d / 2 = 4/2 = 2
- Vier het resultaat: 22 = 4
- Vermenigvuldig met pi: EEN = 4π = 12,56 m2
- Bijvoorbeeld: wat is het oppervlak van een cirkel met een straal van 3 m?
-
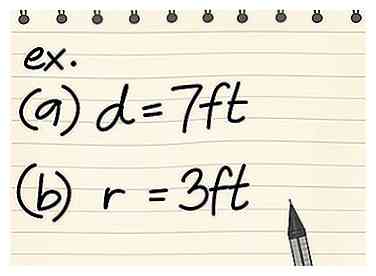 5 Oefen met een paar voorbeelden. Nu je de formule hebt geleerd, is het tijd om te oefenen met een paar voorbeelden. Hoe meer problemen u oplost, hoe gemakkelijker het wordt om ze in de toekomst op te lossen.
5 Oefen met een paar voorbeelden. Nu je de formule hebt geleerd, is het tijd om te oefenen met een paar voorbeelden. Hoe meer problemen u oplost, hoe gemakkelijker het wordt om ze in de toekomst op te lossen. - Zoek het gebied van een cirkel met een diameter van 7 ft.
- A = π (d / 2)2 = π(7/2)2 = π(3.5)2 = 12,25 * π = 38,47 ft2.
- Zoek het gebied van een cirkel met een straal van 3 ft.
- A = πr2 = π32 = 9 * π = 28,26 ft2
- Zoek het gebied van een cirkel met een diameter van 7 ft.
Derde deel van de drie:
Gebied en omtrek berekenen met variabelen
-
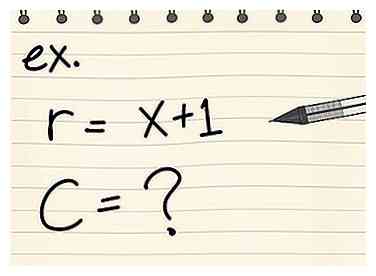 1 Bepaal de straal of diameter van de cirkel. Sommige problemen geven u een straal of diameter met een variabele erin: r = (x + 7) of d = (x + 3). In dit geval kun je nog steeds het gebied of de omtrek oplossen, maar je uiteindelijke antwoord bevat die variabele ook. Noteer de straal of diameter zoals deze in het probleem wordt vermeld.
1 Bepaal de straal of diameter van de cirkel. Sommige problemen geven u een straal of diameter met een variabele erin: r = (x + 7) of d = (x + 3). In dit geval kun je nog steeds het gebied of de omtrek oplossen, maar je uiteindelijke antwoord bevat die variabele ook. Noteer de straal of diameter zoals deze in het probleem wordt vermeld. - Bijvoorbeeld: bereken de omtrek van een cirkel met een straal van (x = 1).
-
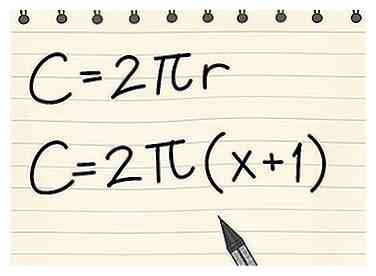 2 Schrijf de formule met de gegeven informatie. Of u nu een probleem oplost voor het gebied of de omtrek, u volgt nog steeds de basisstappen van het aansluiten van wat u weet. Noteer de formule voor het gebied of de omtrek en schrijf vervolgens in de gegeven variabelen.
2 Schrijf de formule met de gegeven informatie. Of u nu een probleem oplost voor het gebied of de omtrek, u volgt nog steeds de basisstappen van het aansluiten van wat u weet. Noteer de formule voor het gebied of de omtrek en schrijf vervolgens in de gegeven variabelen. - Bijvoorbeeld: bereken de omtrek van een cirkel met een straal van (x + 1).
- Schrijf de formule: C = 2πr
- Sluit de gegeven informatie in: C = 2π (x + 1)
-
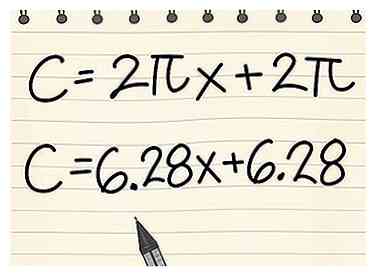 3 Los op alsof de variabele een getal was. Op dit punt kun je het probleem gewoon oplossen zoals je normaal zou doen, de variabele behandelen alsof het gewoon een ander nummer was. Mogelijk moet u de distributieve eigenschap gebruiken om het definitieve antwoord te vereenvoudigen.
3 Los op alsof de variabele een getal was. Op dit punt kun je het probleem gewoon oplossen zoals je normaal zou doen, de variabele behandelen alsof het gewoon een ander nummer was. Mogelijk moet u de distributieve eigenschap gebruiken om het definitieve antwoord te vereenvoudigen. - Bijvoorbeeld: bereken de omtrek van een cirkel met een straal van (x = 1).
- C = 2πr = 2π (x + 1) = 2πx + 2π1 = 2πx + 2π = 6,28x + 6,28
- Als u later in het probleem de waarde "x" krijgt, kunt u deze aansluiten en een heel aantal antwoorden krijgen.
-
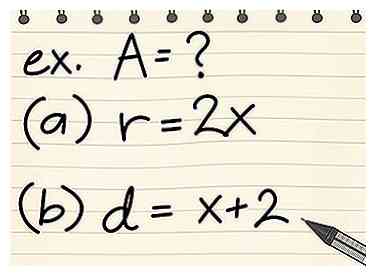 4 Oefen met een paar voorbeelden. Nu je de formule hebt geleerd, is het tijd om te oefenen met een paar voorbeelden. Hoe meer problemen u oplost, hoe gemakkelijker het wordt om ze in de toekomst op te lossen.
4 Oefen met een paar voorbeelden. Nu je de formule hebt geleerd, is het tijd om te oefenen met een paar voorbeelden. Hoe meer problemen u oplost, hoe gemakkelijker het wordt om ze in de toekomst op te lossen. - Zoek het gebied van een cirkel met een straal van 2x.
- A = πr2 = π (2x)2 = π4x2 = 12.56x2
- Zoek het gebied van een cirkel met een diameter van (x + 2).
- A = π (d / 2)2 = π ((x +2) / 2)2 = ((x +2)2/4)π
- Zoek het gebied van een cirkel met een straal van 2x.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Leer de formule voor omtrek. Er zijn twee formules die kunnen worden gebruikt om de omtrek van een cirkel te berekenen: C = 2πr of C = πd, waarbij π de wiskundige constante is die ongeveer gelijk is aan 3,14,[4]r is gelijk aan de straal, en d is gelijk aan de diameter.[5]
1 Leer de formule voor omtrek. Er zijn twee formules die kunnen worden gebruikt om de omtrek van een cirkel te berekenen: C = 2πr of C = πd, waarbij π de wiskundige constante is die ongeveer gelijk is aan 3,14,[4]r is gelijk aan de straal, en d is gelijk aan de diameter.[5]  2 Begrijp de verschillende delen van de formule. Er zijn drie componenten voor het vinden van de omtrek van een cirkel: straal, diameter en π. De straal en diameter zijn gerelateerd: de straal is gelijk aan de helft van de diameter, terwijl de diameter gelijk is aan de dubbele straal.
2 Begrijp de verschillende delen van de formule. Er zijn drie componenten voor het vinden van de omtrek van een cirkel: straal, diameter en π. De straal en diameter zijn gerelateerd: de straal is gelijk aan de helft van de diameter, terwijl de diameter gelijk is aan de dubbele straal. 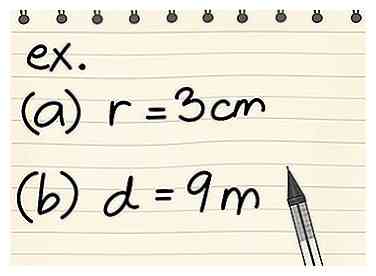 3 Meet de straal of diameter van de cirkel. Gebruik een liniaal, plaats het ene uiteinde aan een kant van de cirkel en plaats het door het middelpunt naar de andere kant van de cirkel. De afstand tot het middelpunt van de cirkel is de straal, terwijl de afstand tot het andere uiteinde van de cirkel de diameter is.
3 Meet de straal of diameter van de cirkel. Gebruik een liniaal, plaats het ene uiteinde aan een kant van de cirkel en plaats het door het middelpunt naar de andere kant van de cirkel. De afstand tot het middelpunt van de cirkel is de straal, terwijl de afstand tot het andere uiteinde van de cirkel de diameter is. 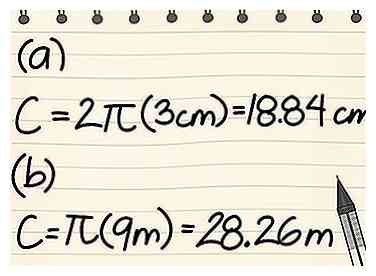 4 Sluit de variabelen aan en los het op. Nadat u de straal en / of diameter van de cirkel hebt bepaald, kunt u deze variabelen in de juiste vergelijking invoegen. Als u de straal hebt, gebruik dan C = 2πr, maar als je de diameter hebt, gebruik dan C = πd.
4 Sluit de variabelen aan en los het op. Nadat u de straal en / of diameter van de cirkel hebt bepaald, kunt u deze variabelen in de juiste vergelijking invoegen. Als u de straal hebt, gebruik dan C = 2πr, maar als je de diameter hebt, gebruik dan C = πd. 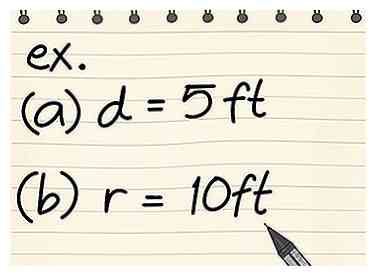 5 Oefen met een paar voorbeelden. Nu je de formule hebt geleerd, is het tijd om te oefenen met een paar voorbeelden. Hoe meer problemen u oplost, hoe gemakkelijker het wordt om ze in de toekomst op te lossen.
5 Oefen met een paar voorbeelden. Nu je de formule hebt geleerd, is het tijd om te oefenen met een paar voorbeelden. Hoe meer problemen u oplost, hoe gemakkelijker het wordt om ze in de toekomst op te lossen.  1 Leer de formule voor het gebied van een cirkel. Het oppervlak van een cirkel kan worden berekend met behulp van de diameter of de straal met twee verschillende formules: A = πr2 of A = π (d / 2)2,[8] waarbij π de wiskundige constante is die ongeveer gelijk is aan 3,14,[9]r is gelijk aan de straal, en d is de diameter.
1 Leer de formule voor het gebied van een cirkel. Het oppervlak van een cirkel kan worden berekend met behulp van de diameter of de straal met twee verschillende formules: A = πr2 of A = π (d / 2)2,[8] waarbij π de wiskundige constante is die ongeveer gelijk is aan 3,14,[9]r is gelijk aan de straal, en d is de diameter.  2 Begrijp de verschillende delen van de formule. Er zijn drie componenten voor het vinden van de omtrek van een cirkel: straal, diameter en π. De straal en diameter zijn gerelateerd: de straal is gelijk aan de helft van de diameter, terwijl de diameter gelijk is aan de dubbele straal.
2 Begrijp de verschillende delen van de formule. Er zijn drie componenten voor het vinden van de omtrek van een cirkel: straal, diameter en π. De straal en diameter zijn gerelateerd: de straal is gelijk aan de helft van de diameter, terwijl de diameter gelijk is aan de dubbele straal. 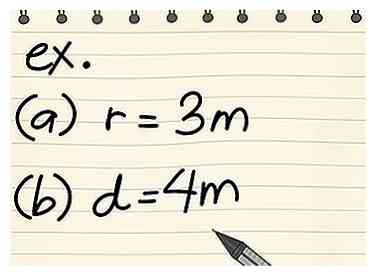 3 Meet de straal of diameter van de cirkel. Gebruik een liniaal, plaats het ene uiteinde aan een kant van de cirkel en plaats het door het middelpunt naar de andere kant van de cirkel. De afstand tot het middelpunt van de cirkel is de straal, terwijl de afstand tot het andere uiteinde van de cirkel de diameter is.
3 Meet de straal of diameter van de cirkel. Gebruik een liniaal, plaats het ene uiteinde aan een kant van de cirkel en plaats het door het middelpunt naar de andere kant van de cirkel. De afstand tot het middelpunt van de cirkel is de straal, terwijl de afstand tot het andere uiteinde van de cirkel de diameter is. 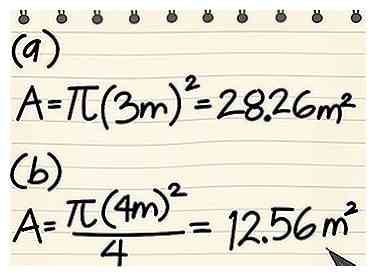 4 Sluit de variabelen aan en los het op. Nadat u de straal en / of diameter van de cirkel hebt bepaald, kunt u deze variabelen in de juiste vergelijking invoegen. Als u de straal hebt, gebruik dan A = πr2, maar als je de diameter hebt, gebruik dan A = π (d / 2)2.
4 Sluit de variabelen aan en los het op. Nadat u de straal en / of diameter van de cirkel hebt bepaald, kunt u deze variabelen in de juiste vergelijking invoegen. Als u de straal hebt, gebruik dan A = πr2, maar als je de diameter hebt, gebruik dan A = π (d / 2)2.  5 Oefen met een paar voorbeelden. Nu je de formule hebt geleerd, is het tijd om te oefenen met een paar voorbeelden. Hoe meer problemen u oplost, hoe gemakkelijker het wordt om ze in de toekomst op te lossen.
5 Oefen met een paar voorbeelden. Nu je de formule hebt geleerd, is het tijd om te oefenen met een paar voorbeelden. Hoe meer problemen u oplost, hoe gemakkelijker het wordt om ze in de toekomst op te lossen. 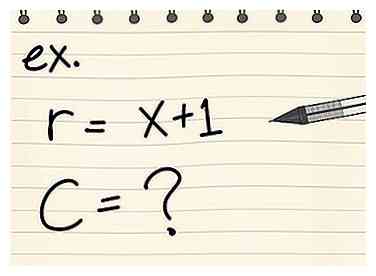 1 Bepaal de straal of diameter van de cirkel. Sommige problemen geven u een straal of diameter met een variabele erin: r = (x + 7) of d = (x + 3). In dit geval kun je nog steeds het gebied of de omtrek oplossen, maar je uiteindelijke antwoord bevat die variabele ook. Noteer de straal of diameter zoals deze in het probleem wordt vermeld.
1 Bepaal de straal of diameter van de cirkel. Sommige problemen geven u een straal of diameter met een variabele erin: r = (x + 7) of d = (x + 3). In dit geval kun je nog steeds het gebied of de omtrek oplossen, maar je uiteindelijke antwoord bevat die variabele ook. Noteer de straal of diameter zoals deze in het probleem wordt vermeld. 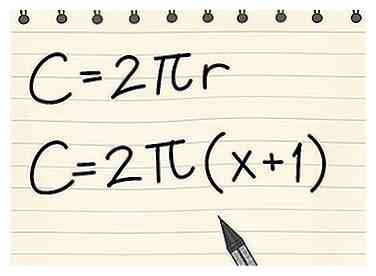 2 Schrijf de formule met de gegeven informatie. Of u nu een probleem oplost voor het gebied of de omtrek, u volgt nog steeds de basisstappen van het aansluiten van wat u weet. Noteer de formule voor het gebied of de omtrek en schrijf vervolgens in de gegeven variabelen.
2 Schrijf de formule met de gegeven informatie. Of u nu een probleem oplost voor het gebied of de omtrek, u volgt nog steeds de basisstappen van het aansluiten van wat u weet. Noteer de formule voor het gebied of de omtrek en schrijf vervolgens in de gegeven variabelen. 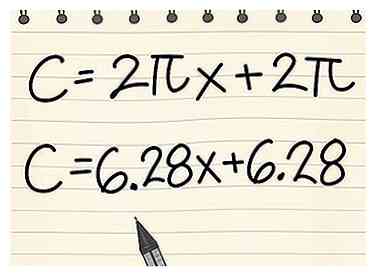 3 Los op alsof de variabele een getal was. Op dit punt kun je het probleem gewoon oplossen zoals je normaal zou doen, de variabele behandelen alsof het gewoon een ander nummer was. Mogelijk moet u de distributieve eigenschap gebruiken om het definitieve antwoord te vereenvoudigen.
3 Los op alsof de variabele een getal was. Op dit punt kun je het probleem gewoon oplossen zoals je normaal zou doen, de variabele behandelen alsof het gewoon een ander nummer was. Mogelijk moet u de distributieve eigenschap gebruiken om het definitieve antwoord te vereenvoudigen. 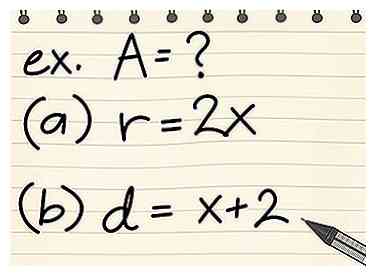 4 Oefen met een paar voorbeelden. Nu je de formule hebt geleerd, is het tijd om te oefenen met een paar voorbeelden. Hoe meer problemen u oplost, hoe gemakkelijker het wordt om ze in de toekomst op te lossen.
4 Oefen met een paar voorbeelden. Nu je de formule hebt geleerd, is het tijd om te oefenen met een paar voorbeelden. Hoe meer problemen u oplost, hoe gemakkelijker het wordt om ze in de toekomst op te lossen.